当前位置：文档之家 › 简谐振动的旋转矢量图示法 PPT

简谐振动的旋转矢量图示法 PPT

  • 格式：ppt
  • 大小：267.00 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

简谐运动及其旋转矢量表示法简谐运动的能量

简谐运动及其旋转矢量表示法简谐运动的能量
解：(1 )A6 1 2 0 m , /3 ，
1 Hz , 2 6
T 2 1 6s, /4
（2）势能 总能
Epkx2/2, EkA 2/2
由题意， k2 x/2k2 A /4, xA/ 24.2 41 02m
（3）从平衡位置运动到 xA/ 2
的最短时间为 T / 8。
即为 6/80.75s
) )
O
A/2
x
(B)
A/2
O
x
A
x 10-2cos( t /3 - /4)，(SI)
五、两个同频率简谐运动的相位关系
x 10-2cos( t /3 - /4)，(SI)
x2 比 x1 超前
简谐运动及其旋转矢量表示法简谐运动的能量
五、两个同频率简谐运动的相位关系
(或 x1 比 x2 落后 ) 的最短时间为 T / 8。
x Acos( t )
半径
圆周运动小球 角速度
振幅
角频率 简谐振动物体
角坐标
相位
例：一物体做谐振动，振幅为 A，在起始
时刻质点的位移为 A/2 且向 x 轴的正方向
运动，代表此谐振动的旋转矢量图为：
质点运动的周期和振幅。
五、两个同频率简谐运动的相位关系
= 2 v = 2 /T
质点运动的周期和振幅。
A
，振幅A=1 cm． t=0时,速度具有负最O大值，求振动表达式．
(C ) x A/2
(D)
A/2
O
x
A
[D]
四、简谐运动的能量
1. 动能
Ek
1 mv 2
2
1 kA2 sin 2( t )
2
掌握
Ek max

《大学物理》第14章 振动

《大学物理》第14章 振动
速度超前位移 /2 vmax = A = (k/m)1/2A
a = - 2A cos (t + ) = 2A cos (t + + )
加速度超前位移 amax = 2A = (k/m)A
上页 下页 返回 退出
相位和初相
相位 (t 0 ) ：决定简谐运动状态的物理量。
其中v为物体 m 距平衡位置 x 处的速度。 忽略摩擦，总机械能 E 保持不变。随着 物体来回振动，势能和动能交替变化。
上页 下页 返回 退出
§ 14-3简谐振动的能量
在x = A 和 x = - A处，v = 0,
E = m(0)2/2 + kA2/2 = kA2/2 (14-10a) 简谐振子的总机械能正比于振幅的平方。
dx/dt = - A sin (t + ) d2x/dt2 = - 2 A cos (t + ) = - 2 x
0 = d2x/dt2 + (k/m) x = - 2 x + (k/m) x
(k/m - 2) x = 0 只有当 (k/m - 2) = 0 时，x不为零。因此
a = - (410 m/s2) cos(1650t). (c) 在t = 1.0010-3 s 时刻
x = A cos t
= (1.510-4 m) cos[(1650 rad/s)(1.0010-3 s)]
= (1.510-4 m) cos(1.650 rad/s) = -1.210-5 m.
上页 下页 返回 退出
§ 14-1 弹簧的振动
例题 14-1 汽车弹簧。当一个质量为200公斤的 一家四口步入一辆总质量为1200公斤的汽车 里，汽车的弹簧压缩了3厘米。(a) 假设汽车 里的弹簧可视为单个弹簧，弹簧劲度系数为 多少？ (b) 如果承载了300公斤而不是200公 斤，则汽车将下降多少厘米？

第四章 振动学基础§4.2简谐振动的图示法.讲解

第四章 振动学基础§4.2简谐振动的图示法.讲解

cos(t) x 1
A2
t π 或 5π
33
由旋转矢量图可知 t π
3
v A sint
A
o A Ax
2
0.26m s1
（负号表示速度沿 Ox轴负方向）
2019/6/11
重庆邮电大学理学院
17
（3）如果物体在 x 0.05m 处时速度不等于零，而是具有 向右的初速度 v0 0.30m s，1 求其运动方程.
A
aቤተ መጻሕፍቲ ባይዱ
x
由图看出：速度超前位移 π 加速度超前速度 2
位移与加速度 Δ π 称两振动反相
若 0 称两振动同相
8、 在谐振动的合成中，用旋转矢量非常方便。
总之20，19/6旋/11 转矢量法在大学物重庆理邮电，大电学理路学院分析，等学科中有广泛15应用
例4.2.4 如图所示，一轻弹簧的右端连着一物体，弹簧的劲度
22
重庆邮电大学理学院
418
例4.2.5、一作简谐振动的物体，其振动曲
x/m
线如图所示。试写出该振动的表达式。
解：振动方程为 x Acos(t )
0.01
由振动曲线可知，振幅为 A 0.02 m
t = 0 时，
x0

A 2

0.01m
O
1
t/s
且其初始速度 v0 0
0.02
y
作旋转矢量图，如右图。

)
2
0 a v
(t )
2
v Asin(t )
x an r 2 A2
a

an
i
(t ) an i cos

大学物理B(Ⅱ)旋转矢量

大学物理B(Ⅱ)旋转矢量
2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示，求振动周
期.
t(s) t 0

A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ，求 1）如图简谐运动方
A＇
44
因为 v0 0 ，由旋转矢量图可知 ＇ π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动，其振
幅为 0.08m，周期为 4s ，起始时刻物体在 x 0.04m
处，向 Ox轴负方向运动（如图）.试求
（1）t 1.0s 时，物体所处的位置和所受的力；
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m

02简谐振动的运动学精品PPT课件

02简谐振动的运动学精品PPT课件

19
t t
o
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x 轴
上的投影点的
运动为简谐运
动.
第4章 机械振动
4–2 简谐振动的运动学
20
y
vm t π
2
t an
A
0
a
v
x
x Acos(t )
vm A v A sin(t )
an A 2
a A 2 cos(t )
雌性蚊子 雄性蚊子 苍蝇 黄蜂
355~415 455~600 330 220
第4章 机械振动
4–2 简谐振动的运动学
例 如图所示系统（细线的质 量和伸长可忽略不计），细线 静止地处于铅直位置，重物位 于O 点时为平衡位置.
若把重物从平衡位置O 略 微移开后放手, 重物就在平衡 位置附近往复的运动．这一振 动系统叫做单摆. 求单摆小角 度振动时的周期．
12
x 简谐运动中， x和 v
间不存在一一对应的关系. A
x A cos(t 0 ) o
v A sin(t 0 ) A
v v
T 2
xt 图
v T t
3、位相和初位相 t 0
1） t 0 (x, v) 存在一一对应的关系;
2）相位在 0 ~ 2π 内变化，质点无相同的运动状态；
相差 2nπ (n为整数 )质点运动状态全同.（周期性）
4–2 简谐振动的运动学
1
一 简谐振动的运动学方程
d2x 2x 0
dt 2
x Acos(t 0 )
cos(t
0
)
sin(t
0
2
)

10-1 简谐振动的矢量图示法

10-1 简谐振动的矢量图示法
简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律：
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置，它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
解：已知 A = 0.12 m，T = 2s，
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时，
x = 0.06， v ＞0， 初相 φ = －π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为：
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M

振动力学教程PPT课件

振动力学教程PPT课件

动的叠加-----------谐波分析
•
2、非周期：利用傅立叶积分作谐波分析
• δ函数又称为单位脉冲函数-----它的性质、应用
示成一系列简谐振
第22页/共35页
第一节：简谐振动及其表示方法
•一、简谐振动的表示方法
• （一）正弦函数表示
2、A、ω、Φ ------简谐振动三要素
第23页/共35页
第24页/共35页
船舶的模态分析和强度分析，飞行器的结构振动和声疲劳分析等。
3） 在土木建筑、地质工程中：建筑、桥梁等结构物的模态分析，地震
引起结构物的动态响应，爆破技术的研究等。
4） 在医学、生物工程中：脑电波、心电波、脉搏波动等的信号处理等。
第12页/共35页
2途径：
1）从具体的工程对象提炼出力学模型 2）建立数学模型------应用力学知识建立所研究问题的数学模型 3）对数学模型进行分析和计算，求出请确、近似或数值解。 4） 比较------将计算结果与工程问题的实际现象或实验研究的测试结果进行 比较，考察理论结果是否解决该工程问题，如不能解决而数学模型及求解均无错 误，则需要修改力学模型重复上述过程。
第9页/共35页
5 随机振动
20世纪50年代，航空和航天工程的发展对振动力学提出了更高 的要求，确定性的力学模型无法处理包含随机因素的工程问题----如大气湍流引起的飞机颤振、喷气噪音导致飞行器表面结构 的声疲劳、火箭运载工具有效负荷的可靠性等。工程的需要迫使 人们用概率统计的方法研究承受非确定性载荷的机械系统和结构 的响应、稳定性和可靠性等， 从而 形成了随机振动这一振动力 学的重要组成部分。 在工程问题中振动信号的采集和处理是随机振动理论应用的前提， 由于计算机的迅速发展和快速第1傅0页/立共35叶页 变换算法的出现，随机振动

1.2旋转矢量与振动的相

1.2旋转矢量与振动的相

1A : A 0.12 m 2 1 2 : S T 3 :
当t＝０时，x０＝０.06m， 带入表达式
x x0 0.12cos 0.06
1 cos 2
,
3

17
第1章 振 动
大学 物理学
1.2
旋转矢量与振动的相
另一个初始条件：当t＝０时，质点向x轴正向运动
v0 0 x A coswt v A sinwt
即： 当t＝０时，
v0 A sin 0


3
sin 0 3

x 0.12 cos t m 或x 0.12 cos t SI 3 18 3 振动 第1章
A2
O
x1
x
x A1
反相
T
A2 o - A2 -A1
t
x2
此种情况称为两振动反相（振动步调完全相反）
第1章 振 动
12
大学 物理学
1.2
旋转矢量与振动的相
Q2 t 0
3若 2 1 0
X2先于x1到达平衡位置、 负的最大等 称为： X2超前于x1， x1 落后于 X2
x
x
o
a
若此时 矢量末端在m点：则当t ，x , v 0
第1章 振 动
8
大学 物理学
1.2
旋转矢量与振动的相 m
x
A A2
a
b
v0
t
tb
a
o
A
v
A
p1 x o Ap2t A
2 n
v0
可以证明：当矢量处于x轴上面，则v<0；反之则v>0 由x~t图象可知：当处于b点时，v<0 所以此时矢量末端在m点

第四章振动下

第四章振动下

结论： 结论：
振子在振动过程中， （1） 振子在振动过程中，动能和势能分别随时间 变化，但任一时刻总机械能保持不变。 变化，但任一时刻总机械能保持不变。 （2） 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时， （3）频率一定时，谐振动的总能量与振幅的平方 成正比。（适合于任何谐振系统） 。（适合于任何谐振系统 成正比。（适合于任何谐振系统） 弹性势能
小结：
描述简谐振动的三种方法： 描述简谐振动的三种方法： 运动方程，振动曲线，旋转矢量。 运动方程，振动曲线，旋转矢量。
的简谐振动， 例1：一物体沿 轴作振 幅为 A 的简谐振动，若初始时该球的 ：一物体沿x轴作振 状态为（ ） ；（2）在平衡位置且向X轴正方向运动 轴正方向运动； 状态为（1）X0＝ -A；（ ）在平衡位置且向 轴正方向运动； ；（ 处向X轴负方向运动；（4） 轴负方向运动；（ （3）在 X0＝1／2 A 处向 轴负方向运动；（ ）在 ） ／ 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求： ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解：
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0

3.简谐运动的图像和公式

3.简谐运动的图像和公式

旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
简谐运动的位移公式:
x Acos( t )
其中A表示振幅, 是圆频率(或称角频率),( t + )称
为物体在t时刻振动的相位(或相)。 是t =0时的相位，
称为初相位，简称为初相。
物体振动状态由相位( t + )决定
旋转矢量
为了直观地表明简谐运动的三个特征量的物理意义，
可用一个旋转矢量来表 示简谐运动。
A
t=t
t = 0
t+
A
o
x·
x
x Aco（s t ）
因此，以o为圆点，旋转矢量A的末端在ox轴上的
投影点的运动是简谐运动。
参考圆
用旋转矢量图画简谐运动的 x t 图
T 2π （旋转矢量旋转一周所需的时间）
2:1 1:1 0
1.相位是用来描述一个周期性运动的物体在一个周期内所 处的不同运动状态的物理量.
2.
x=Asin（ωt＋ φ ）
其中x代表质点对于平衡位置的位移，t代表时间，ω叫做 圆频率，ωt＋φ表示简谐运动的相位.
3.两个具有相同圆频率ｗ的简谐运动，但初相分别为φ１ 和φ2，它们的相位差就是 (ωt+ φ 2)－（ωt＋ φ １）＝ φ 2－ φ 1
知识应用： 1.一质点作简谐运动，图象如图所示，在0.2s 到0.3s这段时间内质点的运动情况是 （ CD ）
A．沿负方向运动，且速度不断增大 B．沿负方向运动的位移不断增大 C．沿正方向运动，且速度不断增大 D．沿正方向的加速度不断减小
弹力、动能、 势能、机械能、 动量呢？

简谐振动旋转矢量法讲课文档

简谐振动旋转矢量法讲课文档
机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——几率波
振动学是波动学的基础
第5章 机械振动
振动: 任何一个物理量(物体的位置, 电 流强度, 电场强度, 磁场强度等)在某一 固定值附近作往复变化. 机械振动: 物体在固定位置(平衡位置) 附近作来回往复的运动. 简谐运动: 是最基本, 最简单的振动.
ω 6π 6
第18页，共20页。
§ 5.3 单摆
O
l T
mg
小球受力矩:
Mmg siln
根据转动定律
M J
mgslinm2ldd2t2
化简得:
d2
dt2
gsin
l
0
当θ 很小时, sin
d2
dt2
g l
0
结论: 单摆振动是简谐运动
0 cos t
g
l
T 2π l g
θ为振动角位移,θ0叫做角振幅
第19页，共20页。
例3: 一简谐振动曲线如图所示, 则振动周期
x（m 4） 2
1
t（s）
2 4 cos
0 4cos
3
32
5
6
T 2 12 5
（A）2.62 s （B）2.40 s （C）0.42 s （D）0.382 s
答案: B
第20页，共20页。
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
依题意, v＜0
v 0.24 3 0.208 m s1 2
第11页，共20页。
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法

简谐振动的旋转矢量图示.ppt

简谐振动的旋转矢量图示.ppt

角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
3、两个谐振动的相位差
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
相位差为 (t 2 ) (t 1) 2 1
采用旋转矢量表示为：
A2
2
A1
1
O
x
例1、两个同频率的谐振动，它们都沿x轴振动，且振
幅相等，当t =0时质点1在x=A/2处向左运动,另一质点
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
（2）由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
在t =T/4=0.5s时，可得
可得x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
（2）由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2

物理-简谐振动的基本特征与旋转矢量图示法

物理-简谐振动的基本特征与旋转矢量图示法

研究简谐振动的重要性
机械振动的分类（从振动形式分） 连续振动、非连续振动； 周期振动、非周期振动…；
最简单、最基本的振动 —— 简谐运动.
简谐运动
合成 分解
复杂振动
机械振动第一讲
简谐振动的基本特征 旋转矢量图示法
一、简谐振动的定义
简谐振动
物体运动过程中，如果离开平衡位置的位 移（或角位移）按余弦函数（或正弦函数） 的规律随时间变化的运动，称为简谐振动。
三、简谐振动的三个特征量
4、振幅(A)与初相()的确定
设
注意 应根据
的符号确定 的象限范围。
三、简谐振动的三个特征量
讨论：两个同频谐振动的振动步调关系
谐振动1 x1 A1 cos(t 1 )
谐振动2 x2 A2 cos(t 2 )
相位差 (t 2 ) (t 1) 2 1
x
1）若 2 1 0
2
x轴负方向运动，而质点2在-A处。
试用旋转矢量法求这两个谐振动的初相差，及 两个质点第一次通过平衡位置的时刻。
四、简谐振动的旋转矢量图示法
小结：用旋转矢量法求相位或相位差的
O
x
第一步：由质点的位移x的值确定旋转矢量动端投影点 在x轴上的位置；
第二步：过该点作x轴的垂线，与矢量参考圆交于两点； 第三步：由质点振动速度的方向确定旋转矢量的位置。
运动学方程： 2、圆频率（ω）
最小正周期
完成一次全振动所需的时间
振动周期
振动频率 （系统固有）
三、简谐振动的三个特征量
运动学方程：
3、初相（ ）
振动速度 振动加速度
若A与确定：物体在t时刻的（x,v,a） 仅由( t + ) 决定。 称( t + ) 为物体在 t 时刻振动的相位(或)。 t =0 时的相位 ——初相位（或初相）

旋转矢量法

旋转矢量法

2.旋转矢量图法及其应用同学们好！旋转矢量法可以形象地表示简谐振动位移和时间关系，便于确定初相位，研究振动的合成。

下面我们一起学习旋转矢量法。

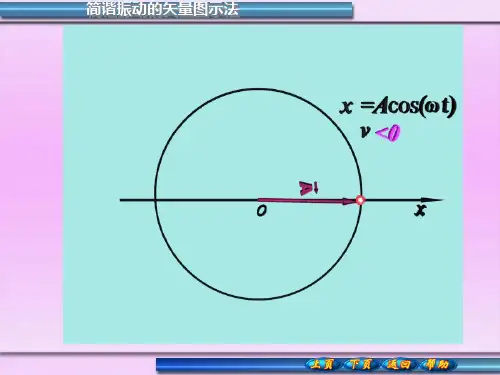
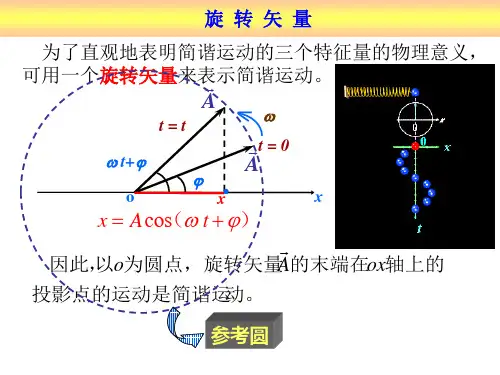
简谐振动的平衡位置为坐标原点O 点，水平向右为轴正方向，自原点O 点做一个矢量，矢量长度等于振幅A ，叫振幅矢量。

初始时刻，矢量A 与x 轴夹角等于振动的初相位ψ。

矢量A 从这位置以ω的角速度沿逆时针方向匀速转动，在任一时刻t ， 矢量A 与轴所成角度为ωt+ψ。

矢量A 在轴上的投影点与简谐振子的小球同步运动，位移相等，它在x 轴上的投影与时间用关系可用简谐振动方程表示。

矢量A 旋转一周，同时矢量的矢端在轴上的投影点完成一次简谐振动，投影点的运动可以形象地表示简谐振动，这种方法叫做旋转矢量法。

使用旋转矢量法还可以形象地了解简谐振动的振幅、角频率、初相位的物理意义。

显然，矢量A 做圆周运动的周期对应简谐振动的周期T ；矢量A 的圆周运动角速度对应简谐振动的角频率ω；初始时刻，旋转矢量的角度对应简谐振动的初相位ψ。

另外，使用旋转矢量法可以方便的确定物体的振动状态或初相位。

1. 由相位确定振动状态(1)简谐振动的相位是π/3，求振动状态I .旋转矢量图中，矢量A 的相位等于π/3，矢量A 的投影是物体的位移，等于A /2, 下一时刻矢量A 逆时针转动，所以简谐振动的小球向x 轴负方向运动。

(2)如果简谐振动的相位等于3π/2，求振动状态。

在旋转矢量图中，矢量A 的相位等于3π/2，矢量的投影点在x 轴的投影恰好在原点O , 所以物体的位移等于0， 矢量A 做逆时针转动，所以简谐振动的小球向x 轴正方向运动。

x x x2.由振动状态求初相位初始时刻，简谐振动的物体位移是A/2, 物体向x轴正方向运动，也就是速度大于0，初相位是多少？图中，矢量A在x轴的投影是A/2，表明矢量在第一或第四象限，且投影点向x轴正方向运动，从图示来看矢量A只能在第四象限。

因此初相位等于5π/3或-π/3。

机械振动——简谐运动的基本概念2

机械振动——简谐运动的基本概念2
4．振动的合成(第 6 节内容) 例：一个质点沿 x 轴作简谐运动，振幅 A=0.06m，周期 T=2s，初始时刻质点位 于 x0=0.03m 处且向 x 轴正方向运动。求： （1）初相位； （2）在 x=-0.03m 处且 向向 x 轴负方向运动时物体的速度和加速度以及质点从这一位置回到平衡位置 所需要的最短时间。 解： （1）取平衡位置为坐标原点，质点的运动方程可写为
两边对时间求导，得
1 dv 1 dx m ⋅ 2v + k ⋅ 2 x =0 2 dt 2 dt
即
m⋅v
d 2x + k ⋅ xv = 0 dt 2 d 2x k + x=0 dt 2 m
令ω ＝
2
k ，则 m d 2x +ω2x = 0 2 dt
其解为
x = A′ cos(ωt + ϕ )
代入守恒方程可得 A=A’ 例 2．劲度系数为 k、原长为 l、质量为 m 的匀质弹簧，一端固定，另一端系一 质量为 M 的物体，在光滑的水平面上作直线运动，求其运动方程。
v A＝ x + 0 ω
2 0
2
二、能量平均值 定义：一个随时间变化的物理量 f(t)，在时间 T 内的平均值定义为
114
机械振动——简谐振动的基本概念
f =
1 f (t )dt T∫ 0 1 1 1 1 2 2 2 2 2 2 ∫ 2 mA ω sin (ωt + ϕ )dt = 4 mA ω = 4 kA T 0 1 1 2 1 2 1 2 2 2 ∫ 2 kA cos (ωt + ϕ )dt = 4 kA = 4 mA ω T 0
113
机械振动——简谐振动的基本概念
简谐运动的能量

§3.2 简谐振动的旋转矢量图示【VIP专享】

§3.2 简谐振动的旋转矢量图示【VIP专享】
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
（2）由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
（2）由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
dt
3
在t =T/4=0.5s时，可得
x (0.08m) cos[(π s1)t π ] 3
2
3
v0 0
π
3
A
π3
x/m
0.08 0.04 o 0.04 0.08
x (0.08m) cos[(π s1)t π ]
2
3
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
t 1.0s 代入上式得 x 0.069m
2
3
v
x/m
0.08 0.04 o 0.04 0.08
cos( t ) 1
23 2
t 2 或 4
233 3
又因为第一次到达- 0.04m处时，v 0
即v A sin(t ) 0
23
所以t 2
23 3
t 2s 3

5-2 旋转矢量

5-2 旋转矢量

20 10 0 , 20 10
表示 x2 振动超前 x1 振动Δφ。
20 10 0 , 20 10
表示 x2 振动滞后 x1 振动Δφ。
x
2 超前于1 或 1滞后于 2
4）研究简谐振动位移、速度、加速度之间的相位关系
x A cos( t 0 ) p v A sin( t 0 ) v m cos( t 0 ) 2 2 a A cos( t 0 ) am cos( t 0 p )

π
t 3
o
π 3
0.04 0.08
x/m
π 1 s 2 t 0.667 s
π t 3
0.08 0.04
5 – 2 旋转矢量 补充例题 一质点沿x轴作简谐振动，振幅A＝0.05m， 周期 T＝0.2s。当质点正越过平衡位置向负 x 方向时开 始计时。 （1）写出此质点的简谐运动的表达式； （2）求在 t＝0.05s 时质点的位置、速度和加速度； （3）另一质点和此质点的振动频率相同，但振幅为 0.08m，并和此质点反相，写出另一质点的简谐运动表 达式； （4）画出两振动的相量图 解： x
T/4 T/4
x a o
T t

vm
r A
900 900
am
t+

x
v
0 0
r r p 由图可见： v 超前 x 2
o
·

r r p a 超前 v 2
例1 如图所示，一轻弹簧的右端连着一物体，弹簧的劲度系 1 数 k 0.72N m，物体的质量 m 20g . （1）把物体从平衡位置向右拉到 x 0.05 m 处停下后再释放， 求简谐运动方程； （2）求物体从初位置运动到第一次经过

11-1简谐振动旋转矢量表示法

11-1简谐振动旋转矢量表示法

以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第十一章 振 动
3
大学物 理学
1111-1 简谐振动的旋转矢量表示法
ω
t =t
ωt + ϕ
v A
x
o
x = A cos(ωt + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
x1 = A1 cos(ωt + ϕ1 ) x2 = A2 cos(ωt + ϕ 2 )
∆ϕ = (ωt + ϕ 2 ) − (ωt + ϕ1 )
∆ϕ = ϕ 2 − ϕ1
第十一章 振 动
10
大学物 理学
1111-1 简谐振动的旋转矢量表示法
∆ϕ = ϕ 2 − ϕ1
∆ϕ = 0 同步
∆ϕ = ±π 反相 ∆ϕ为其它
简谐运动， （1）对同一简谐运动，相位差可以给出 ） 同一简谐运动 两运动状态间变化所需的时间． 两运动状态间变化所需的时间．
x1 = A cos(ωt1 + ϕ )
x2 = A cos(ωt 2 + ϕ )
∆ϕ = (ωt2 +ϕ) −(ωt1 +ϕ)
∆t = t2 −t1 = ∆ϕ
ω
第十一章 振 动
x = 0.104m v = −0.188m / s 2 a = −1.03m / s
A
− 0.12 −0.06
t 时刻
x/m
0.12
起始时刻
15
o
π − 3
0.06
A
第十一章 振 动
ω
大学物 理学

4.3 简谐振动的旋转矢量法

4.3 简谐振动的旋转矢量法

2
大学物理
第一版
4.3 简谐振动的旋转矢量法
t t
A
o

t
x
以o 为原点 旋转矢量 A 的 端点在 x轴上的 投影点的运动为 简谐运动.
x A cos(t )
3
大学物理
第一版
4.3 简谐振动的旋转矢量法
x A cos(t )
以o 为原点 的端 旋转矢量 A 点在 x 轴上的投 影点的运动为简 谐运动.
讨论

相位差：表示两个相位之差
（1）对同一简谐运动，相位差可以给出两运 动状态间变化所需的时间．
x1 Acos( )
t t 2 t1
x2 Acos( t2 )

9
大学物理
第一版
4.3 简谐振动的旋转矢量法
vm A
A
x A cos(t )
v a

v A sin(t )
x a A 2 n
a A 2 cos( t )
7
大学物理
第一版
4.3 简谐振动的旋转矢量法
3
用旋转矢量图画简谐运动的
xt 图
8
大学物理
第一版
4.3 简谐振动的旋转矢量法
0.08
17
大学物理
第一版
4.3 简谐振动的旋转矢量法
法二
t
时刻

t
π3 π3
起始时刻
x/m
0.08
0.08 0.04
o
0.04
π π 2 1 rad s t 0.667 s t 3 2 3
18
大学物理
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解法一(解析法）:
(1)取平衡位置为坐标原点,谐振动方程写为：
xAcos(t0)
由条件 T=2s可得
22 s1
T2
5
由初始条件 t = 0, x=0.06m可得
0 .1 2 c o s0 0 .0 6 即 c o s0 0 .5
0
3
或
3
由于t=0时质点向x轴正向运动可知
v0Asin00
因而
正方向运动,求运动方程。
解：(1) k 0.726.0s-1
m 0.02
由旋转矢量可知初相位 0 0
谐振动方程为
0.05
O
x
x0.05cos(6.0t) m 12
(2) v dx 0.056.0sin(6.0t) dt
=0.3sin(6.0t) m/s
第一次经过A/2时，相位
6.0t 3
t2 1.83s
因此从x = -0.06m处第一次回到平衡位置的时间：
tt2t10.83s
8
大家有疑问的，可以询问和交流
可以互相讨论下，但要小声点
9
解法二(旋转矢量法）:
(1)
0
O
x = 0.06m x t=0时旋转矢量
0
5
3
或
3
x0.12cos(t) m
3
10
(2)与解析法同
(3) x = -0.06m
0 3
简谐振动表达式
x0.12cos(t) m
3
6
(2)由简谐振动的运动方程可得:
vdx0.12sin(t) m /s
dt
3
adv 0.12 2cos(t)m /s2
dt
3
在t =T/4=0.5s时，可得
x0.12cos(0.5)0.104m
v 0 .1 2 sin ( 0 .5 3) 0 .1 8m /s
1
O
x3
例1、两个同频率的谐振动，它们都沿x轴振动，且 振幅相等，当t =0时质点1在x=A/2处向左运动,另 一质点2在x=-A/2处向右运动，试用旋转矢量法 求两质点的相位差。
解： 1
3
2
4
3
2
1
A 2
AA O2
x
2143 3
4
例2、一物体沿x轴作简谐振动，振幅A=0.12m,周期 T=2s。当t=0时,物体的位移x=0.06m,且向x轴正向运 动。求: (1)简谐振动表达式; (2) t=T/4时物体的位置、速度和加速度； (3)物体从x =-0.06m向x轴负方向运动，第一次回到 平衡位置所需时间。
a 0 .1 2 2c o s( 0 .5 3 ) 1 .0 3m /s2
3
7
(3Q )c当vo0 sx( =t1- 0.0A 36sm)in 时(，t121该时3刻)设0为tt11,得3t1 233或 2433
t1 1 s
3 设物体在t2时刻第一次回到平衡位置，相位是 2
t2
3
3
2
14
§3.2 简谐振动的旋转矢量图示法
旋转矢量:一长r 度等于
Mω
振幅A 的矢量 在A 纸平面
t
内绕O点沿逆时针方向旋
r A
转，其角速度大小与谐振
动的角频率相等，这个矢
t 0
t=0
量称为旋转矢量
M 点在 x 轴上投影点(P点)的运动规律：
xAcos(t0)
1
说明：
1、旋转矢量的方向: 逆时针方向
x = -0.06m时 旋转矢量
O
x
第一次回到平衡 位置时旋转矢量
5
32 6
5 t 6 50.83s
6 11
例3、一弹簧振子 k 0 .7 2 N /m ,m 2 0 g (1)将物体从平衡位置向右拉到 x=0.05m 处释放,求谐振
动方程. (2)求物体第一次经过A/2 处时速度大小。 (3)如果物体在x=0.05m处速度大小为 v0.30m/s ,且向
r 2、旋转矢量 A
和谐振动
xAcos(t0)
的对应关系
r A
的长度
振幅A
Ar旋转的角速度
角频率ω
r
A 与参考方向x 的夹角
振动相位ωt+φ0
2
3、两个谐振动的相位差
x1A1cos(t1) x2A2cos(t2)
相位之差为 (t 2 ) (t 1 ) 2 1
r
采用旋转矢量表示为：
A2
2
r A1
O
A 2
x
v 0.3sin () 0.33 0.26m /s
3
2
13
(3) 由初始条件，t=0,v0=0.30m/s, x0=0.05m,可得
A x02 v022 0.0707m
0arctan （ xv0 0 ） =arctan （ 1）
0
4
或 3
4
0.05
由旋转矢量
0
4
O
x
运动方程
x0.0707cos(6.0t )m 4