旋转矢量法

旋转矢量法在简谐振动中的应用探讨摘要：结合旋转矢量法的理论依据探究旋转矢量法在简谐振动中的应用，探究结果发现：旋转矢量法的理论依据是两个振幅相等，频率相同的简谐振动，相位差等于π/2，沿垂直方向的合成就是圆周运动；而旋转矢量法可计算简谐振动的矢端速度与加速度、相位与初相位、运动时间间隔及合振动。

关键词：旋转矢量法；简谐振动；应用0.旋转矢量法旋转矢量法[1]，也叫匀速圆周运动法，参考圆法，用其方法来解决简谐振动中的问题，相对来说比较简单。

如图1，做一个圆周，以O为原点，向右为正方向建立坐标轴，根据题目条件确定半径位置，要观察的是半径的端点在x轴上的投影的位置，如果速度为正，半径端点一定处于x轴下方，反之在x轴上方，比如，t＝0时，质点正经过平衡位置向正方向运动，那么这个半径端点就是在原点正下方，即端点的投影刚好在原点[2]。

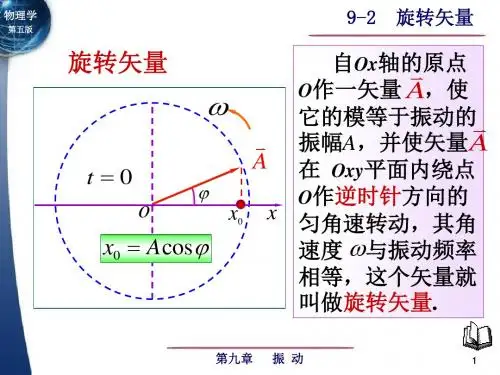
而以O为原点的旋转向量A的端点与在x 轴上的投影点的运动为简谐振动。

图1 旋转矢量图2 相位差为π/2互相垂直简谐振动的合成1.简谐振动矢量法的理论依据互相垂直相同频率简谐振动的合成[3]，现将分振动的运动学方程表示为，，质点既沿Ox轴又沿Oy轴运动，实际上是在Oxy平面上运动。

从上面方程消去t，得合振动的轨迹方程：=。

当相位差为时，，表明合振动的轨迹为以x和y为轴的椭圆，如图2所示这里又可分为两种情况，时，x方向的振动比y方向的振动超前，即，当某一瞬时，则x=0，y=A2，即质点在图2(a)中的P点，经过很短时间后略大于零，y将略小于A2，为正，而略大于，x将为负，故质点运动到第二象限，即质点沿椭圆逆时针运动。

反之，时，y方向的振动比x方向的振动超前，质点沿椭圆顺时针方向运动，如图2（b）。

以上两分运动中，若=且相位差为，则其合运动轨迹方程褪化为圆。

两个振幅相等，频率相同的简谐振动，相位差等于沿互相垂直方向合成的为圆周运动；反推理可得，圆周运动亦能分解为两互相垂直的同振幅同频率的简谐振动。

旋转矢量法的原理和应用1. 原理介绍旋转矢量法是一种用于描述物体在三维空间中进行旋转的数学方法。

它通过使用矢量的旋转运算来表示物体的旋转姿态。

旋转矢量法基于欧拉角的表达方式，但它使用四元数来进行计算，避免了欧拉角的一些问题，例如万向锁问题。

2. 旋转矢量的表示旋转矢量通常由一个单位四元数表示，该四元数可以表示物体绕任意轴的旋转。

一个旋转矢量可以通过一个轴向量和一个旋转角度来确定。

轴向量定义了旋转轴的方向，旋转角度表示物体绕轴旋转的量。

3. 旋转矢量的计算为了应用旋转矢量进行对象的旋转，需要进行一些数学计算。

首先，需要将旋转矢量转换为一个旋转矩阵。

然后，可以使用该旋转矩阵将对象的顶点或其他坐标进行变换，以实现旋转效果。

4. 旋转矢量的应用旋转矢量法在计算机图形学和游戏开发中得到了广泛应用。

它可以用于实现物体的旋转、旋转动画和摄像机的旋转等效果。

此外，旋转矢量法还可以用于物体的插值和平滑过渡，例如在两个姿态之间进行插值，以实现流畅的动画效果。

5. 旋转矢量法的优势相比于传统的欧拉角表示，旋转矢量法具有以下几个优势： - 万向锁问题：使用旋转矢量法可以避免欧拉角的万向锁问题，使得旋转计算更加稳定和可靠。

- 插值效果：旋转矢量法可以实现更顺滑的插值效果，使得物体在动画中的过渡更加自然。

- 计算效率：由于使用四元数进行计算，旋转矢量法通常比欧拉角计算更快，尤其是在需要进行大量的旋转计算时。

6. 示例应用场景下面是一些示例应用场景，展示了旋转矢量法的一些实际应用： - 3D建模软件：在3D建模软件中，旋转矢量法被用于实现物体的旋转和变换操作，帮助用户进行建模和设计。

- 游戏开发：旋转矢量法在游戏开发中被广泛使用，用于实现游戏角色的旋转、摄像机的控制以及动画的实现。

- 航空航天领域：旋转矢量法可以应用于飞行器的姿态控制，帮助飞行器保持平稳的飞行姿态和准确的导航。

7. 总结旋转矢量法是一种用于描述物体旋转的数学方法，通过使用旋转矢量来表示物体的旋转姿态。

旋转矢量法详细讲解
旋转矢量法是一种常用的三维刚体运动描述方法，它可以描述刚体在空间中的旋转状态。

本文将详细介绍旋转矢量法的原理、应用以及计算方法。

一、原理
旋转矢量法的基本原理是将刚体的旋转运动分解为绕三个互相垂直的轴的旋转运动的组合。

这三个轴分别称为x轴、y轴和z轴，它们的方向与刚体的坐标系有关。

在旋转矢量法中，用一个三维向量来表示刚体的旋转状态，这个向量被称为旋转矢量。

二、应用
旋转矢量法广泛应用于机械工程、航空航天、地球物理学等领域。

在机械工程中，旋转矢量法可以用于描述机械零件的旋转状态，从而进行运动学和动力学分析。

在航空航天领域，旋转矢量法可以用于描述飞行器的姿态和轨迹，从而进行导航和控制。

在地球物理学中，旋转矢量法可以用于描述地球的自转和地震波的传播，从而进行地震学研究。

三、计算方法
旋转矢量的计算方法有多种，其中最常用的是欧拉角法和四元数法。

欧拉角法是将旋转运动分解为三个绕不同轴的旋转运动的组合，然后通过三个角度来描述这三个旋转运动的大小和方向。

四元数法是将旋转运动表示为一个四元数，通过四元数的乘法和加法来描述旋转运动的组合。

四、总结
旋转矢量法是一种常用的三维刚体运动描述方法，它可以描述刚体在空间中的旋转状态。

旋转矢量法广泛应用于机械工程、航空航天、地球物理学等领域。

旋转矢量的计算方法有多种，其中最常用的是欧拉角法和四元数法。

掌握旋转矢量法的原理和计算方法，对于进行三维刚体运动分析和控制具有重要的意义。

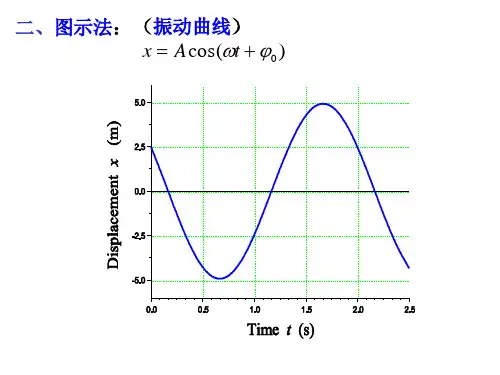
2.旋转矢量图法及其应用同学们好！旋转矢量法可以形象地表示简谐振动位移和时间关系，便于确定初相位，研究振动的合成。

下面我们一起学习旋转矢量法。

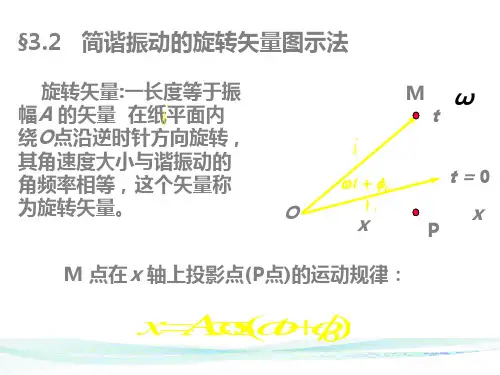
简谐振动的平衡位置为坐标原点O 点，水平向右为轴正方向，自原点O 点做一个矢量，矢量长度等于振幅A ，叫振幅矢量。

初始时刻，矢量A 与x 轴夹角等于振动的初相位ψ。

矢量A 从这位置以ω的角速度沿逆时针方向匀速转动，在任一时刻t ， 矢量A 与轴所成角度为ωt+ψ。

矢量A 在轴上的投影点与简谐振子的小球同步运动，位移相等，它在x 轴上的投影与时间用关系可用简谐振动方程表示。

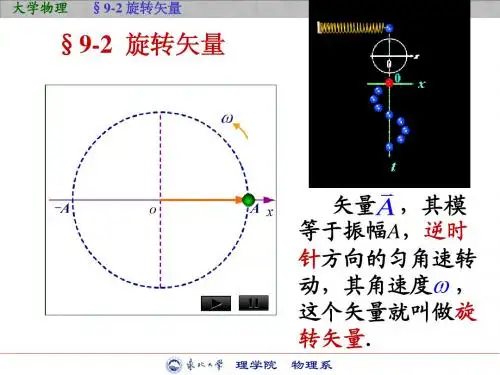
矢量A 旋转一周，同时矢量的矢端在轴上的投影点完成一次简谐振动，投影点的运动可以形象地表示简谐振动，这种方法叫做旋转矢量法。

使用旋转矢量法还可以形象地了解简谐振动的振幅、角频率、初相位的物理意义。

显然，矢量A 做圆周运动的周期对应简谐振动的周期T ；矢量A 的圆周运动角速度对应简谐振动的角频率ω；初始时刻，旋转矢量的角度对应简谐振动的初相位ψ。

另外，使用旋转矢量法可以方便的确定物体的振动状态或初相位。

1. 由相位确定振动状态(1)简谐振动的相位是π/3，求振动状态I .旋转矢量图中，矢量A 的相位等于π/3，矢量A 的投影是物体的位移，等于A /2, 下一时刻矢量A 逆时针转动，所以简谐振动的小球向x 轴负方向运动。

(2)如果简谐振动的相位等于3π/2，求振动状态。

在旋转矢量图中，矢量A 的相位等于3π/2，矢量的投影点在x 轴的投影恰好在原点O , 所以物体的位移等于0， 矢量A 做逆时针转动，所以简谐振动的小球向x 轴正方向运动。

x x x2.由振动状态求初相位初始时刻，简谐振动的物体位移是A/2, 物体向x轴正方向运动，也就是速度大于0，初相位是多少？图中，矢量A在x轴的投影是A/2，表明矢量在第一或第四象限，且投影点向x轴正方向运动，从图示来看矢量A只能在第四象限。

因此初相位等于5π/3或-π/3。

旋转矢量法求初相位概述及解释说明1. 引言1.1 概述旋转矢量法是一种用于求解信号初始相位的数学方法，广泛应用于信号处理领域。

在许多实际问题中，准确确定信号的初相位对于数据分析和系统性能评估至关重要。

通过应用旋转矢量法，我们可以有效地估计信号的初相位，并将其应用于各种领域，如通信、雷达、图像处理等。

1.2 文章结构本文将按照以下结构进行介绍和解释：- 引言部分将对旋转矢量法求初相位的背景和意义进行概述。

- 旋转矢量法求初相位的理论基础将在第2节中详细阐述。

- 第3节将解释和说明旋转矢量的定义、性质以及该方法在信号处理中的作用。

- 第4节将介绍相关实验验证和结果分析。

- 最后一节为总结与展望，对本文内容进行概括，并探讨旋转矢量法求初相位在未来的应用前景。

1.3 目的本文的目的是全面介绍旋转矢量法求初相位这一方法，并从理论到实践层面进行详细阐述。

通过对方法的解释和说明，我们将揭示旋转矢量法在信号处理中的作用以及确定初相位的优势和局限性。

此外，通过实验验证和结果分析，我们将进一步验证该方法的有效性并提供相关数据支持。

最终，本文旨在为读者提供一个清晰全面的概述，并展望旋转矢量法求初相位在未来应用中可能发挥的重要作用。

2. 旋转矢量法求初相位2.1 理论基础旋转矢量法是一种用于求解信号的初相位的方法，基于信号在复平面上的表示和分析。

该方法利用了旋转矢量在复平面上的特性，通过对信号进行复数域运算和变换，得到信号的频率和初相位信息。

在时域中表示的信号可以看作是复平面上绕原点进行旋转的矢量。

根据欧拉公式，可以将一个复数表示为振幅与相位之间关系的指数形式：A*e^(jφ)，其中A为振幅，φ为相位角。

2.2 方法步骤旋转矢量法求解信号的初相位主要包括以下几个步骤：步骤1：获取待处理的信号数据，并进行预处理。

这一步通常包括去除噪声、滤波和采样等操作，以确保信号质量。

步骤2：对信号进行傅里叶变换或小波变换等频域变换，得到信号在频域上的表示。

旋转矢量法详细讲解
旋转矢量法是一种常用的三维空间中的旋转变换方法，它可以将一个三维向量绕着某个轴旋转一定的角度，从而得到一个新的向量。

这种方法在计算机图形学、机器人学、航空航天等领域都有广泛的应用。

旋转矢量法的基本思想是，将旋转变换分解为两个步骤：先将原向量绕着一个固定的轴旋转到一个特定的位置，再将其绕着另一个轴旋转到最终的位置。

这两个步骤可以用两个旋转矩阵来表示，它们的乘积就是最终的旋转矩阵。

具体来说，假设我们要将一个向量v绕着轴n旋转θ角度，那么首先需要将v投影到n所在的平面上，得到一个新的向量v'。

然后，将v'绕着n旋转θ/2角度，得到一个新的向量v''。

最后，将v''再绕着n的负方向旋转θ/2角度，就得到了最终的旋转向量。

旋转矢量法的优点在于，它可以避免旋转矩阵中的奇异性问题，从而提高计算的稳定性和精度。

此外，它还可以方便地进行复合旋转，即将多个旋转变换组合起来进行计算。

需要注意的是，旋转矢量法只适用于绕着固定轴进行旋转的情况，如果需要进行任意方向的旋转，就需要使用四元数或欧拉角等其他方法。

旋转矢量法是一种简单而有效的三维旋转变换方法，它在计算机图
形学、机器人学、航空航天等领域都有广泛的应用。

掌握旋转矢量法的原理和应用，对于进行三维空间中的旋转变换具有重要的意义。

旋转矢量法
矢量分析是研究数量物理学中最重要的方法之一，也是数学上最重要的分析工具之一。

矢量是两个平行线段（或者轴），用两个点表示，一个点是矢量的“起点”，另一个点是“终点”。

矢量的长度是从矢量的起点到终点的距离。

此外，矢量具有向量的属性，如方向和向量的场性质。

矢量的分析应用于几何、力学和电磁学等领域。

旋转矢量法（RVM）
旋转矢量法是一种应用于矢量分析的经典方法，它可以用于计算矢量的图形表示，也可以用于计算基本的向量图形。

一般来说，旋转矢量法是一种可以将一个向量从一个坐标系统转换到另一个坐标系统的方法。

原理介绍
旋转矢量法的基本原理是使用两个向量的叉积来旋转一个向量到另一个坐标系统，这两个向量分别称为被旋转矢量和旋转矢量。

如果从一个坐标系(A)旋转到另一个坐标系(B)，则使用被旋转矢量与旋转矢量的叉积，即可计算出旋转矢量在坐标系B中的表达式。

旋转矢量法还可以用来求解向量平面间的夹角和两个向量分量的夹角。

应用
旋转矢量法可用于计算图形学中的位置和方向，也可以应用于机器人、空间分析和三维图形模拟等技术。

此外，旋转矢量法还可以用于解决由向量和仿射变换组成的更复杂的数学问题。

总结
本文简要介绍了旋转矢量法，这是一种矢量分析的经典方法，可以用于计算矢量的图形表示和基本的向量图形，也可以用于解决由向量和仿射变换组成的更复杂的数学问题。

矢量分析方面的必要知识是可以理解旋转矢量法的基础，它需要计算坐标系之间的变换，以及向量的方向和向量的场性质。

在机器人，空间分析和三维图形模拟等技术中，旋转矢量法可以用于计算位置和方向。