轴对称及其应用

课时四 轴对称的综合应用
轴对称的综合应用：
1. 轴对称在工程建设中的应用：
桥梁、大型水库及水利结构、导线桥架、护坡墙、山坡防护、立交桥、悬索桥等工程建设中，都有广泛的应用轴对称的结构，大大提高工程施工的效率。

2. 轴对称在加工制造中的应用：
在汽车车门、汽车大灯、机床、飞机、家具等制造行业，都需要轴对称结构，使其表面形状更富有艺术美感。

3. 轴对称在构件制造中的应用：
轴对称构件可以使材料的流动更加有效，相比于传统的构件，其机械强度更高、机动性更好。

4. 轴对称在建筑构件上的应用：
轴对称构件可以有效地增加结构刚度，如螺旋楼梯、钢结构、悬臂梁等结构，都需要轴对称结构。

5. 轴对称在能源行业的应用：
在能源行业，轴对称的结构作为机械装置的成分，可以在机械驱动、电气机械设备等方面起到重大的作用。

6. 轴对称在精密仪器设备中的应用：
精密仪器设备中有大量采用轴对称结构，可以减少振动幅度，提高精度、操作便捷性，确保精密仪器设备的运行稳定性。

7. 轴对称在装饰艺术品中的应用：
轴对称能够体现设计师的艺术感知和自由发挥，使艺术品更加具有欣赏性，同时使整体结构更加独立、区别，使得艺术品更加完整美观。

第三讲 轴对称的性质及其应用知识要点： 1、轴对称及其性质把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫对称轴。

轴对称的两个图形有如下性质：①关于某直线对称的两个图形是全等形；②对称轴是任何一对对应点所连线段的垂直平分线；③两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。

2、线段垂直平分线线段垂直平分线也叫线段中垂线，它反映了与线段的两种关系：①位置关系——垂直； ②数量关系——平分。

性质定理：线段垂直平分线上的点与这条直线线段两个端点的距离相等。

判定定理：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

3、当已知条件中出现了等腰三角形、角平分线、高（或垂线），或求几条折线段的最小值等情况时，通常考虑作轴对称变换，以“补齐”图形，集中条件。

4、生活中的图形折叠实质是轴对称，此外，还有生活中的照镜子，人、像与镜子的距离保持相等，人、像关于镜面的对称叫镜面对称，如果把镜面用一条直线表示，人和像的一个侧面用平面图形表示，那么人、像关于镜子的对称轴也是轴对称。

例1 △ABC 中，∠C=90°，点A 关于BC 边的对称点为A '，点B 关于AC 边的对称点为B '，点C 关于B A '边的对称点为C '，若a S ABC =∆，求C B A S ''∆和四边形B A AB ''的面积（用a 的代数式表示）。

A 'B 'B例2 如果，现有人骑马从C 点到D 点，但必须先到河岸1l 处的1P 点去让马饮水，然后再到河岸2l 处的2P 点再次让马饮水，最后到D 点，他如何选择饮水点1P 、2P ，才能使所走的L 2L 1D路程D P P P CP 2211++为最短？'L 2L 1例3 如图，P 为ABC ∆边BC 上的一点，且P C ＝2PB ，已知︒=∠45ABC ，︒=∠60APC ，求ACB ∠的度数。

轴对称、中心对称图形的性质及应用一、轴对称图形如果把一个图形沿着某一条直线对折过来，在直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴，能够重合的点互为对称点．轴对称图形具有以下的性质：(1)轴对称图形的两部分是全等的；(2)对称轴是连结两个对称点的线段的垂直平分线．在几何证题、解题时，如果是轴对称图形，则经常要添设对称轴以便充分利用轴对称图形的性质．譬如，等腰三角形经常添设顶角平分线；矩形和等腰梯形问题经常添设对边中点连线和两底中点连线；正方形，菱形问题经常添设对角线等等．另外，如果遇到的图形不是轴对称图形，则常选择某直线为对称轴，补添为轴对称图形，或将轴一侧的图形通过翻折反射到另一侧，以实现条件的相对集中．例1 已知直线l外有一定点 P，试在l上求两点A、B，使AB＝m(定长)，且PA＋PB最短．分析当把P点沿l方向平移至C(如图1)，使PC＝m，那么问题就转化为在l上求一点B，使CB＋PB为最短．作法过P作PC∥l，使PC＝m，作P关于l的对称点P＇，连结CP＇交l于B．在l上作AB＝m，点A、B为所求之两点．证在l上另任取A＇B＇＝m，连PA、PA＇、PB＇，CB＇，A＇P＇，B＇P＇，则PA＇＝P＇A＇，PB＇＝P＇B＇，又PA＇B＇C 为平行四边形，∴CB＇＝PA＇．∵CB＇＋B＇P＇＞CP＇，∴ PA＇＋PB＇＞PA＋PB．例2 如图2，△ABC中，P为∠A外角平分线上一点，求证：PB＋PC＞AB＋AC．分析由于角平分线是角的对称轴，作AC关于AP的轴对称图形AD，连结DP、CP，则DP＝CP，BD＝AB＋AC．这样，把 AB＋AC、AC、PB、PC集中到△BDP中，从而由PB＋PD＞BD，可得PB＋PC＞AB＋AC．证 (略)说明通过变为轴对称图形后，起到相对集中条件的作用，又有将折线化直的作用(如AB＋AC化直为BD)．例3 等腰梯形的对角线互相垂直，且它的中位线等于m，求此梯形的高．解如图3．设等腰梯形AD∥BC，AB＝DC，对角线AC与BD相交于O，且AC⊥BD，中位线EF＝m．过AD、BC的中点M、N作直线，由等腰梯形ABCD关于直线MN成轴对称图形，∴O点在MN上，且OA＝OD，OB＝OC，AM＝DM，BN＝CN．又 AC⊥BD，故△AOD和△BOC均为等腰直角三角形．2OM＝AD，2ON＝BC．∵AD＋BC＝2EF＝2m，∴2OM＋2ON＝2m．∴OM＋ON＝m，即梯形高MN＝m．例4 凸四边形EFGH的四个顶点分别在边长为a的正方形ABCD的四条边上．证如图4，连结AA2，EE3．正方形ABCD和正方形A1BCD1关于BC对称；EFGH和E1FG1H1关于BC对称；A1BCD1和A2B1CD1关于 CD1对称；E1FG1H1和 E2F1G1H2关于CD1对称；A2B1CD1和A2B2C1D1关于A2D1对称，E2F1G1H2和E3F2G2H2关于A2D1对称．例5 如果一个四边形关于它的两组对边中点的两条连线成轴对称，则此四边形为矩形．已知如图22－5．四边形ABCD中，M、F、N、E分别为各边的中点，且MN、EF为它的对称轴．求证 ABCD是矩形．分析欲证ABCD是矩形，首先证明它是平行四边形，再证明它有一个直角即可．证∵四边形ABCD关于EF成轴对称，∴DC⊥EF，AB⊥EF，∴AB∥DC．同理AD∥BC．∴ABCD是平行四边形．∴DC＝AB．又∵DE＝DC/2，AF＝AB/2．∴DE AF，∴ADEF为平行四边形．∴AD∥EF，而DE⊥EF，∴DE⊥AD，∠D＝Rt∠．∴ABCD是矩形．二、中心对称图形如果把一个图形绕着某一点旋转180°后，能和原图形重合，那么这个图形叫做中心对称图形．这个点叫做对称中心，能重合的点互为对称点．中心对称图形具有以下性质：(1)关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分．(2)关于中心对称的两个图形，对应线段平行(或在同一条直线上)且相等．平行四边形是中心对称图形．矩形、菱形、正方形既是中心对称图形，也是轴对称图形．例6 如图6．已知ABCD，O是对角线 AC与BC的交点． EF过O点与AB交于E，与DC交于F．求证：OE＝OF．证∵O点是ABCD的对称中心，EF过O点与AB相交于E，与DC相交于F．故E、F两点是以点O为对称中心的对称点．∴OE＝OF．例7 △ABC中，底边BC上的两点M、N把BC三等分，BE是AC上的中线，AM、AN分BE 为a，b，c三部分，求：a∶b∶c．分析本题解法很多，我们利用中心对称图形求解．如图7，以E为中心，作已知图形的中心对称图形，则M＇C∥AM，N＇C ∥AN，于是可得a∶(2b＋2c)＝1/2，∴a＝b＋c，①(a＋b)∶2c＝DN＇∶N＇A＝2∶1，∴a＋b＝4c，②由①得，a－b＝c，③②＋③， 2a＝5c，∴a＝5c/2．②－③，2b＝3c，∴b＝3c/2．∴ a∶b∶c＝5c/2∶3c/2∶c＝5∶3∶2．解 (略)例8 若四边形的一组对边相等，延长这一组对边，使各与另一组对边的中点连线的延长线相交，则这两个交角必相等．已知如图8．四边形ABCD中， AD＝BC，E、F分别是AB、CD的中点，AD、BC的延长线分别与EF的延长线交于G、H．求证∠AGE＝∠BHE．分析为了使求证的两个角与已知条件发生联系，利用“旋转法”使角或线段搬家而沟通思路．证如图8，以E为对称中心，作△EBC的中心对称图形△EAM(即连结CE并延长CE到M 使EM＝EC，连结AM)．连结DM，AM＝BC＝AD，∴∠2＝∠3．∵DF＝FC，CE＝EM，∴DM∥HE，∴∠1＝∠2．∵AE＝EB， EM＝EC，∴AMBC是平行四边形．∴AM∥BH，而DA∥HE，∴∠3＝∠BHE．∴∠1＝∠BHE，即∠AGE＝∠BHE．习题1．如图9 一牧童在A处牧马，牧童家在B处．A、B处距河岸分别为300m、500m，CD ＝600m，天黑前，牧童从A点将马牵到河边去饮水后再赶回家．那么牧童最少要走多少米？2．证明：任一点关于正方形各边中点的对称点是一个正方形的顶点．3．求证：在四边形ABCD中，如果AB＝AD，CB＝CD，那么它的面积等于AC·BD/2．4．在直线MN两侧有A，B两点，在MN上求一点P，使P到A、B两点之差最大．5．等腰梯形的周长为22cm，中位线长为 7cm，两条对角线中点连线为3cm，求各边长．。

请简答轴对称原理的应用什么是轴对称原理？轴对称原理是指物体或系统在绕某个轴旋转180度后，仍然具有相同的形状和性质。

这个轴被称为轴对称轴。

轴对称原理是在理解和研究物体结构和性质时经常应用的原理之一。

在物理、化学和工程等领域中，轴对称原理有广泛的应用，可以帮助我们理解和解决各种问题。

轴对称原理的应用1.建筑设计轴对称原理在建筑设计中应用广泛。

建筑物的外立面、室内布局、建筑平面图和立面图等都常常采用轴对称的结构。

轴对称设计不仅能够实现美观和对称感，还有助于保持建筑结构的平衡和稳定性。

2.机械设计在机械设计中，轴对称原理被广泛应用于各种机械零件和设备的设计中。

例如，在设计齿轮、轴承和传动装置时，考虑到轴对称性可以减少噪音和振动，并提高零件的工作效率和寿命。

3.流体力学在流体力学中，轴对称原理被用于研究流体的行为和流动属性。

通过考虑轴对称性，可以简化流体力学问题的计算和分析。

例如，在设计管道系统和液压装置时，轴对称原理可以帮助工程师理解和优化流体的流动过程。

4.生物医学在生物医学领域，轴对称原理被用于理解和研究生物体的结构和功能。

例如，人体的左右对称性是基于轴对称原理的。

轴对称原理也可以应用于器官移植和组织修复等医学应用中。

5.光学设计在光学设计中，轴对称原理被用于设计光学元件和光学系统。

通过利用轴对称性，可以简化光学设计过程，并提高光学系统的性能和效率。

6.电路设计在电路设计中，轴对称原理被用于分析和优化电路的结构和特性。

例如，在设计电路板和电子设备时，考虑到轴对称性可以帮助工程师减少信号干扰和电路噪音，并提高电路的稳定性和可靠性。

总结轴对称原理是一种常用的原理，广泛应用于各个领域。

在建筑设计、机械设计、流体力学、生物医学、光学设计和电路设计等领域中，都可以看到轴对称原理的应用。

通过考虑和利用轴对称性，可以简化问题的分析和解决，提高设计和实施的效率和可靠性。

轴对称图形的性质及应用轴对称图形是指通过对称轴将图形分为两个互补的部分，两侧部分完全对称的图形。

本文将介绍轴对称图形的特点、性质以及在日常生活中的应用。

特点：轴对称图形在对称轴两侧完全对称，也就是说，左右两侧完全相同，而相应的点到对称轴的距离也完全相等。

轴对称图形最简单的例子就是欧拉线。

性质：轴对称图形与一般图形相比，具有许多独特性质。

1.对称坐标：轴对称图形在对称轴两侧完全对称，因此可以将其坐标进行相应的简化，将对称轴视为原点，将图形分解为x轴和y轴两个部分。

这种简化的坐标系统被称为对称坐标系。

2.取消相似性：一个轴对称图形绕对称轴旋转180度后，两部分分别重叠，正反都是一样的。

这也就说明了轴对称图形并不具有缩放不变性。

与此相反，使用其他变换，如旋转和平移时，图形可能变形，但尺寸和形状不变化。

3.构造对称轴：如果给定一个轴对称图形，很容易通过观察来确定它的对称轴。

但是，如果给定一个线段，如何通过它来构造轴对称图形呢？有一种简单的方法是，将线段的中点作为对称轴，然后用半径相等的圆弧将线段两端连接起来，就可以得到一个轴对称图形。

应用：轴对称图形在各个领域都有着广泛的应用。

1.设计：在建筑设计过程中，轴对称设计可以增强结构的平衡和美感。

对称图案也常常出现在布艺和墙壁装饰品上。

2.生物学：轴对称图形在生物学中也有着广泛的应用。

例如，许多植物和动物的身体结构都具有轴对称性。

轴对称性在遗传学中也发挥着重要作用，它对生物特征的分析和研究有重要的指导作用。

3.艺术：轴对称图形是艺术中常常使用的一种形式。

例如，一些字母、标志和图形都是轴对称的，这在机器制图和商业设计中都很常见。

4.数学：轴对称图形在数学中也发挥着重要作用，特别是在几何学中。

几何转化和对称操作常常用于证明数学定理，而轴对称图形则是证明某些性质的好例子。

总结：轴对称图形是一种可以通过对称轴将图形分为两个互补的部分，两侧部分完全对称的图形。

轴对称图形具有特殊的性质，例如对称坐标，取消相似性以及构造对称轴等。

轴对称在生活中的应用我们生活在一个充满对称的世界中，从自然景观到分子结构，从建筑物到艺术作品，甚至日常生活用品，人们都可以找到对称的例子，而轴对称是对称中重要的一种，在日常生活中有着非常重要的应用。

本文试举几例，谈谈轴对称在生活中的应用。

一．利用轴对称巧妙设计, 使所用的输水管线最短例1：如图1，要在河道L上修建一座水泵站，分别向A、B两镇供水，泵站建在河道的什么地方，可使所用的输水管线最短？L（图1）分析：我们可以把河道近似地看成一条直线l，问题就是要在直线L上找一点C，使AC与BC的和最小。

设B’是B关于l 的对称点，本题就是要使AC与CB’的和最小。

在连接AB’的线中，线段AB’最短。

因此，线段AB’与直线l的交点C的位置即为所求。

二．利用轴对称,在台球比赛中准确击球例2：如图2，已知台球桌ABCD内有两球P、Q，现击打球Q 去撞击AD边后反弹，再撞击P球。

请画出Q球撞击AD边的位置。

DC图2分析：要使球Q撞击AD边反弹，再撞击球P,必须使球Q的入射角等于其反射角，显然，作P点关于AD的对称点P’,连结P’Q, P’Q 与AD相交于点E,很容易得到∠QED=∠AEP’=∠AEP。

所以点E即为所求的点。

三．利用轴对称，求出镜中电子钟的实际时刻和水中车牌倒影的实际号码例3.小明从平面镜里看到镜子对面电子钟示数的像如图3所示，这时的实际时刻应该是（）A. 21:10B. 10:21C. 10:51D. 12:013分析：根据镜子中电子钟示数与实际时刻的读数成轴对称，镜子是对称轴，所以在镜中电子钟示数的右边划一条直线作为对称轴，找出各数字的对称图形，立即可以得出这时的实际时刻是10：51，所以选择C.例4．一辆汽车的车牌在水中的倒影如图4所示，请问该车的车牌号码是多少？分析：水中的倒影与实际的车牌号成轴对称，但两组数据的方向是一致的，所以在水中的倒影下边划一条直线作为对称轴，就很容易求得该车的实际车牌号是M17936，本题应和例3区别开来。

轴对称的应用题轴对称是几何学中常见的概念，广泛应用于各个领域。

本文将介绍轴对称在建筑设计、工程机械、电子技术以及生物学等领域的应用。

一、建筑设计中的轴对称应用轴对称在建筑设计中具有重要的作用。

建筑物的外观通常需要具备美观和稳定的特征，而轴对称是实现这一目标的重要手段之一。

在建筑物的立面设计中，设计师通常会沿着某条中心线进行对称排列，使得建筑物在外观上呈现出左右对称的形态，给人以和谐、稳定的感觉。

此外，轴对称也常用于室内空间的布局，以增加空间的舒适度和平衡感。

二、工程机械中的轴对称应用在工程机械设计中，轴对称同样扮演着重要角色。

例如，挖掘机的前后部件往往呈现对称排列，这样可以使得机械运动更加平衡稳定。

此外，在液压系统设计过程中，轴对称的排列有助于维持系统的稳定性，提高机械的工作效率。

在工程机械制造过程中，轴对称也广泛运用于零部件的制造和加工，以保证零部件的质量和可靠性。

三、电子技术中的轴对称应用在电子技术领域，轴对称同样具有重要意义。

例如，在半导体器件的设计中，轴对称布局有助于减小布线长度以及降低电路的互感干扰，从而提高电路的性能和稳定性。

此外，轴对称的设计还可以提供更加均匀的电磁场分布，有利于电子设备的工作效率和可靠性。

四、生物学中的轴对称应用轴对称在生物学领域中也有广泛的应用。

例如，在生物体结构的研究中，轴对称往往是不同器官和组织之间协作的基础。

生物体的肢体、器官等结构通常都是沿着中心轴对称排列，这有助于提高生物体的运动协调性和平衡性。

此外，轴对称的研究也对于生物进化和分类学具有重要的意义，它可以帮助科学家理解生物体的发育过程以及不同物种之间的相似性和差异性。

总结：通过对轴对称在不同领域的应用的讨论，我们可以看到它在各个领域中的重要性。

无论是在建筑设计、工程机械、电子技术还是生物学中，轴对称都可以提高系统的稳定性、性能和可靠性，从而对相应领域的发展和进步起到积极的促进作用。

因此，深入理解和应用轴对称的原理和方法，对于相关领域的专业人士是至关重要的。

轴对称图形在建筑中的应用（优秀成果）摘要本文介绍了轴对称图形在建筑中的应用，并展示了一些优秀的成果。

轴对称图形是指在某一条轴线上两侧的形状完全相同或镜像对称的图形。

这种图形在建筑设计中具有许多优点，包括美学效果、结构稳定性和空间布局的灵活性。

通过几个案例，我们可以看到轴对称图形在建筑中的广泛应用和出色的效果。

1. 美学效果轴对称图形在建筑中的应用可以创造出简洁、对称的外观，给人以美感和和谐感。

例如，许多古代建筑都使用了轴对称布局，如希腊神庙和中国的古代宫殿。

这些建筑以其对称和谐的外观成为了经典之作，为后世建筑师提供了无尽的灵感。

2. 结构稳定性轴对称图形在建筑结构中起到了增强稳定性的作用。

通过在建筑的两侧使用相同的结构元素，可以达到平衡的效果，提高建筑的抗风、抗震等能力。

这对于一些高层建筑或特殊形状的建筑尤为重要。

轴对称图形的应用可以使建筑更加牢固和稳定。

3. 空间布局的灵活性轴对称图形在建筑的空间布局中具有很大的灵活性。

通过将轴对称图形应用于建筑的不同部分，可以创造出多种不同的功能区域和空间感。

例如，在一个建筑中，可以通过在中心轴线上设置中庭或大厅，将两侧的功能区域分隔开来，同时又保持了整体的统一性。

这种灵活性使得轴对称图形成为了建筑师们设计多功能建筑的重要工具。

4. 案例展示4.1 希腊神庙希腊神庙是轴对称图形应用的典范之一。

这些古代建筑以它们简洁而对称的外观而闻名，成为了建筑史上的经典之作。

它们的轴对称布局赋予了这些建筑以庄重和美感。

4.2 吴哥窟吴哥窟是柬埔寨的一处古代建筑遗址，也是轴对称图形应用的杰作之一。

这个庞大的建筑群以其精湛的雕刻和对称的布局而闻名，给人一种宏伟和神秘的感觉。

4.3 现代建筑在现代建筑中，轴对称图形的应用仍然非常广泛。

许多摩天大楼和宫殿都采用了轴对称的设计，以展现出现代建筑的美感和稳定性。

结论轴对称图形在建筑中的应用具有许多优点，包括美学效果、结构稳定性和空间布局的灵活性。

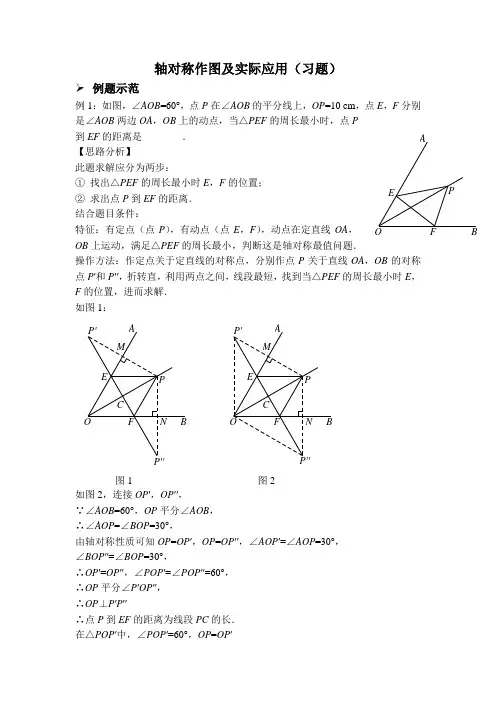
轴对称作图及实际应用（习题）例题示范例1：如图，∠AOB =60°，点P 在∠AOB 的平分线上，OP =10 cm ，点E ，F 分别是∠AOB 两边OA ，OB 上的动点，当△PEF 的周长最小时，点P 到EF 的距离是________． 【思路分析】此题求解应分为两步：① 找出△PEF 的周长最小时E ，F 的位置； ② 求出点P 到EF 的距离． 结合题目条件：特征：有定点（点P ），有动点（点E ，F ），动点在定直线OA ，OB 上运动，满足△PEF 的周长最小，判断这是轴对称最值问题．操作方法：作定点关于定直线的对称点，分别作点P 关于直线OA ，OB 的对称点P ′和P ′′，折转直，利用两点之间，线段最短，找到当△PEF 的周长最小时E ，F 的位置，进而求解． 如图1：P''P'CNM AOB EFPPF EBOAM N CP'图1 图2 如图2，连接OP ′，OP ′′， ∵∠AOB =60°，OP 平分∠AOB ， ∴∠AOP =∠BOP =30°，由轴对称性质可知OP =OP ′，OP =OP ′′，∠AOP ′=∠AOP =30°， ∠BOP ′′=∠BOP =30°，∴OP ′=OP ′′，∠POP ′=∠POP ′′=60°， ∴OP 平分∠P ′OP ′′， ∴OP ⊥P ′P ′′∴点P 到EF 的距离为线段PC 的长． 在△POP ′中，∠POP ′=60°，OP =OP ′P FEBA∴△POP ′是等边三角形 又∵OP ⊥P ′P ′′，OP =10 ∴152P C O P ==巩固练习1. 作已知线段的中点．已知：线段MN ．求作：MN 上一点O ，使OM =ON ．NM作法：（1）分别以_______，_______为圆心，__________为半径作弧，两弧相交于_______和________； （2）___________________________________． ___________________________．2. 已知△ABC ，利用直尺和圆规，根据下列要求作图（不写作法，保留作图痕迹），并填空：（1）作∠ABC 的平分线BD 交AC 于点D ；（2）作线段BD 的垂直平分线交AB 于点E ，交BC 于点F ，交BD 于点O ．由（1），（2）可得：线段EF 与线段OE 的数量关系为______________，并证明．3. 如图，已知∠AOB 的大小为α，P 是∠AOB 内部的一个定点，且OP =2，点E ，F 分别是OA ，OB 上的动点，若△PEF 周长的最小值等于2，则α=________．AB CP FEBA4. 如图，在四边形ABCD 中，∠BAD =120°，∠B =∠D =90°，在BC ，CD 上分别找一点M ，N ．当△AMN 的周长最小时，∠AMN +∠ANM =_________°．ABC DNMD C B A5. 如图，一牧童在A 处放牛，其家在B 处，A ，B 到河岸的距离分别为AC ，BD ，且AC =BD ，已知A 到河岸CD 的中点的距离为500米．牧童从A 处把牛牵到河边饮水后再回家，请作图说明牧童怎样走路程最短，并求出最短路程．思考小结1. 轴对称最值问题的特征及操作D C B A2.如图，在直线l上找一点P，使得在直线同侧的点A，B到点P的距离之和AP+BP最小，并说明理由．BAl思路提示：在l上任取一点P′（P′不与P重合），则AP+BP_____AP′+BP′（填“>”、“<”或“=”）理由如下：①由对称得：AP=_____，AP′=_____；②AP+BP=________=________，AP′+BP′=________；③由_______________________可得AP+BP_____AP′+BP′．【参考答案】1.图略（1）点M，点N，大于1M N长，点A，点B2（2）连接AB交MN于点O点O即为所求2.图略，EF=2OE；证明略3.30°4.∠AMN+∠ANM=120°5.图略，最短路程为1 000米思考小结1. 动点动和最小定点，定直线交点2. ＜①'A P，''A P②'A P+BP=AB；''B PA P+'③三角形两边之和大于第三边，＜。

轴对称图形的性质及应用如果把一个图形沿着某一条直线对折过来，在直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴，能够重合的点互为对称点．轴对称图形具有以下的性质：（1）轴对称图形的两部分是全等的；（2）对称轴是连结两个对称点的线段的垂直平分线．在几何证题、解题时，如果是轴对称图形，则经常要添设对称轴以便充分利用轴对称图形的性质．譬如，等腰三角形经常添设顶角平分线；矩形和等腰梯形问题经常添设对边中点连线和两底中点连线；正方形，菱形问题经常添设对角线等等．另外，如果遇到的图形不是轴对称图形，则常选择某直线为对称轴，补添为轴对称图形，或将轴一侧的图形通过翻折反射到另一侧，以实现条件的相对集中．例1已知直线l 外有一定点 P ，试在l 上求两点A ，B ，使AB m =（定长），且PA PB +最短．分析：当把P 点沿l 方向平移至C （如图1），使PC m =，那么问题就转化为在l 上求一点B ，使CB PB +为最短．作法：过P 作//PC l ，使PC m =，作P 关于l 的对称点P '，连结CP '交l 于B ．在l 上作AB m =，点A ，B 为所求之两点．证：在l 上另任取A B m ''=，连PA ，PA '，PB '，CB '，A P ''，B P ''，则P A PA'''=，PB P B '''=，又PA B C ''为平行四边形，∴CB PA ''=． ∵CB '＋B P ''＞CP '， ∴PA '＋PB '＞PA ＋PB ．例2如图2，△ABC 中，P 为∠A 外角平分线上一点，求证：PB ＋PC ＞AB ＋AC ．分析：由于角平分线是角的对称轴，作AC关于AP的轴对称图形AD，连结DP，CP，则DP＝CP，BD＝AB＋AC．这样，把AB＋AC，AC，PB，PC集中到△BDP中，从而由PB＋PD＞BD，可得PB＋PC＞AB＋AC．证：（略）．点评：通过变为轴对称图形后，起到相对集中条件的作用，又有将折线化直的作用（如AB＋AC化直为BD）．例3等腰梯形的对角线互相垂直，且它的中位线等于m，求此梯形的高．解：如图3．设等腰梯形AD∥BC，AB＝DC，对角线AC与BD相交于O，且AC⊥BD，中位线EF＝m.过AD，BC的中点M，N作直线，由等腰梯形ABCD关于直线MN成轴对称图形，∴O点在MN上，且OA＝OD，OB＝OC，AM＝DM，BN＝CN．又AC⊥BD，故△AOD和△BOC均为等腰直角三角形．2OM＝AD，2ON＝BC．∵AD＋BC＝2EF＝2m，∴2OM＋2ON＝2m．∴OM＋ON＝m，即梯形高MN＝m．例4凸四边形EFGH的四个顶点分别在边长为a的正方形ABCD的四条边上．求证：EFGH的周长不小于．证：如图4，连结AA 2，EE 3．正方形ABCD 和正方形A 1BCD 1关于BC 对称；EFGH和E 1FG 1H 1关于BC 对称；A 1BCD 1和A 2B 1CD 1关于 CD 1对称；E 1FG 1H 1和 E 2F 1G 1H 2关于CD 1对称；A 2B 1CD 1和A 2B 2C 1D 1关于A 2D 1对称，E 2F 1G 1H 2和E 3F 2G 2H 2关于A 2D 1对称．2AA =，又23AE A E =32EE AA ==1122332EF FG GH HE EF FG G H H E EE AA ∴+++=+++==≥例5 如果一个四边形关于它的两组对边中点的两条连线成轴对称，则此四边形为矩形．已知：如图5．四边形ABCD 中，M ，F ，N ，E 分别为各边的中点，且MN ，EF 为它的对称轴．求证：ABCD 是矩形．分析：欲证ABCD 是矩形，首先证明它是平行四边形，再证明它有一个直角即可．证：∵四边形ABCD 关于EF 成轴对称，∴DC ⊥EF ，AB ⊥EF ， ∴AB ∥DC ．同理AD ∥BC ．∴ABCD 是平行四边形．∴DC ＝AB ．又∵2DC DE =，2AB AF =．∴D E AF ，∴ADEF 为平行四边形．∴AD ∥EF ，而DE ⊥EF ，∴DE ⊥AD ，∠D ＝90 ．∴ABCD 是矩形．轴对称应用举例山东 徐传军生活中很多图形的形状都有一个共同的特性———轴对称．在日常生活中利用轴对称的性质能解决很多问题，下面举例说明．一、确定方向例1 如图1，四边形ABCD 是长方形的弹子球台面，有黑白两球分别位于E 、F 两点的位置，试问，怎样撞击黑球E ，才能使黑球先碰撞台边DC ，反弹后再击中白球F ？解：作E 点关于直线CD 的对称点E ′，连接FE ′，与CD 的交点P 即为撞击点，点P即为所求．例2 如图2，甲车从A 处沿公路L 向右行驶，乙车从B 处出发，乙车行驶的速度与甲车行驶的速度相同，乙车要在最短的时间追上甲车，请问乙车行驶的方向？解：作AB 的垂直平分线EF ，交直线L 于点C ，乙车沿着BC 方向行驶即可．二、确定点的位置找最小值例3 如图3，AB ∥CD ，AC ⊥CD ，在AC 上找一点Ｅ,使得BE +DE 最小．解：作点B 关于AC 的对称点B ′,连接DB ′，交AC 于点E ，点E 就是要找的点．例4如图4，点A是总邮局，想在公路L1上建一分局D，在公路L2上建一分局E，使AD+DE+EA的和最小．解：作点A关于L1和L2的对称点B、C．连接BC，交L1于点D，交L2于点E．点D、E就是要找的点．三、与其他学科结合唐朝某地建造了一座十佛寺，竣工时，太守在庙门右边写了一副上联“万瓦千砖百匠造成十佛寺”，望有人对出下联，且表达恰如其分，你能对出下联来吗?对联中有数字万、千、百、十，几个月过去了，无人能对，有个文人李生路过，感觉庙前没有下联不像话，十分感慨．一连几天在庙前苦思冥想，未能对出下联，有次在庙前散步，望见一条大船由远而来，船夫正使劲的摇橹，这时李生突发灵感，对出了下联———“一舟二橹四人摇过八仙桥”．太守再次路过此庙时，看到下联，连连称赞“妙妙妙”．这副对联数字对数字，事物对事物，对称美如此的和谐．可见，对称美在文学方面也有生动深刻的体现．生活中的轴对称无处不在,只要你善于观察,将会发现其间所蕴涵的丰富的文化价值和对称美给人带来的回味无穷的享受．用轴对称解实际问题山东于秀坤在我们实际生活中，许多问题设计到轴对称的应用，下面介绍几例.例1要在河岸所在直线l上修一水泵站，分别向河岸同侧的A、B两村送水，请你设计水泵站应修在何处，所用管道最短？分析：设水泵站修在C点，此题的实质是求折线AC+BC的最短长度，可作出A点关于直线l的对称点A′，如图1，根据对称性，AC+BC=A′C+BC，所以连结BA′交直线l于点C，点C便是水泵站的位置，因为此时折线长AC+CB化成线段A′B的长，根据两点之间线段最短的道理便可确定点C是水泵的位置．图1 图2例2如图2，角形铁架∠MON小于60°，A、D是OM、ON上的点，为实际应用的需要，须在OM和ON上各找点B、C，使AB+BC+CD最小，问应如何找？分析：学习了轴对称，可以利用对称性化折为直的道理，分别作出点A、点D关于ON、OM的对称点A′、D′，连结A′D′与ON、OM交于B、C，则点B、C便是所求的点．例3如图3，EFGH是一个长方形的弹子球台面，有黑白两球分别位于A、B两点的位置．（1）试问：怎样撞击黑球A，使黑球A先碰撞台边EF反弹后再撞击白球B？（2）怎样撞击黑球A，使黑球先碰撞台边GH反弹后再击台边EF，最后击白球B？图3分析：利用轴对称的性质，分别作出B点关于EF的对称点，A点关于HG的对称点，问题得解．解：（1）①作点B关于EF的对称点B′，②连结AB′交EF于C点，则沿AC撞击A，球A必沿BC反弹击中白球B（如图4）．图4 图5（2）如图5，作法类似（1）．例4如图5，小河边有两个村庄，要在河对岸建一自来水厂向A村与B村供水，要符合条件：（1）若要使厂部到A、B的距离相等，则应选在哪儿？（2）若要使厂部到A村、B村的水管最省料，应建在什么地方？图5 图6 图7解：（1）如图6，取线段AB的中点G，过中点G作AB的垂线,交EF于P，则P到A、B的距离相等．（2）如图7，作点A关于河岸EF的对称点A′，连结A′B交EF于P，则P到A、B 的距离和最短．用轴对称知识解决打台球一题山东于秀坤题目：小强和小勇利用课本上学过的知识来进行台球比赛．（1）小强把白球放在如图1所示的位置，想通过击打白球撞击黑球，使黑球撞AC边后反弹进F洞；想想看小强这样击打，黑球能进F洞吗？请画图的方法验证你的判断，并说明理由．图1 （2）小勇想通过击打白球撞击黑球，使黑球至多撞台球桌边一次后进A洞，请你猜想小勇有几种方案？并分别在下面的台球桌上画出示意图，解释你的理由．分析：本题是一道操作型探究题，主要根据轴对称的知识的有关进行探究．第(1)题可以通过击打AC边使球反弹进F洞．第(2)题有多种方法．击球入洞需要对每一杆的角度进行适当的估算，实质上等同于几何角度的计算，二者有着密切的关系．要想至多撞台球桌边一次击黑球于F洞．方案可以有以下情况：(1)不击台球桌边，直接用白球撞击黑球;(2)通过白球击CF边反弹再撞击黑球进A洞；(3)用白球撞击DF边反弹撞击黑球进F洞．要想准确撞击黑球，必须找准击球的方向角度，准确估算击球的方向．在数学上，可以借助轴对称的知识来解决问题．解: (1)如图2，将白球与黑球视为两点，过这两点画直线交台球桌边AC于M，过点M 作法线MN⊥AC，在MN右侧∠F′MN=∠PMN，由于射线MF′过F洞，知黑球经过一次反弹后必进入F洞．图2（2）方案1：如图3，视白球、黑球为两点P，G，使A、G、P在同一直线上．方案2：如图4，延长AC到H点，使AC=CH，连接GH交FC于点K，根据轴对称的知识可知，用白球沿GK方向撞击边CF反弹后可进行A洞．方案3：如图5，延长AD到M点，使MD=AD，连结GM交DF于N，根据轴对称知识可知，沿GN方向用白球撞击黑球经反弹后可进入A洞．图3 图4 图5最短线路问题河北欧阳庆红吴立稳同学们，对于最短线路问题你一定很陌生吧?运动着的车、船、飞机，包括人们每天走路都要遇到这样的问题．古今中外的任何旅行者总希望寻求最佳的旅行路线，尽量走近道，少走冤枉路．我们把这类求近道的问题统称最短线路问题．另外，从某种意义上说，一笔画问题也属于这类问题，这类问题在生产、科研、生活中应用广泛．请同学们看下面几个生活中的最短线路问题．一、两点一线问题例1 如图1，某同学打台球时想绕过黑球，通过击黑球A，使主球A撞击桌边MN后反弹，来击中白球B．请在图中标明，黑球撞在MN上哪一点才能达到目的？(以球心A、B来代表两球)?分析：要撞击黑球A，使黑球A先撞击台边MN上的P点后反弹击中白球B，需∠APN=∠BPM，如图2，可作点A关于MN的对称点A’，连结A’B交MN于点P，则P点即为所求作的点．作法:（图2）：⑴作点A关于MN的对称点A’；⑵连结A’B，交MN于P．则经AP撞击台边MN，必沿P B反弹击中白球B．∴点P就是所要求的点．N图1说明：本题黑球A ，白球B 在MN 的同侧，直接确定撞击点的位置不容易，但若A 、B 在MN 的异侧，击球路线就容易确定了．本题可利用轴对称的特征将A 点转化到MN 的另一侧，设为A ’，连接A ’B 即可确定撞击点．二、一点两线问题例2 在一条大的河流中有一形如三角形的小岛（如图3），岸与小岛有一桥相连．现准备在小岛的三边上各设立一个水质取样点．水利部门在岸边设立了一个观测站，每天有专人从观测站步行去三个取样点取样，然后带回去化验．请问，三个取样点应分别设在什么位置，才能使得每天取样所用时间最短(假设速度一定)? 分析：此题要求时间最短，而速度一定，所以可转化为求最短路程．如图4，小桥DE为必走之路，所以容易得到D 为BC 边上的取样点．关键是确定另外两边上的取样点，这是线段之和最小的问题，我们的想法是将三条线段拼起来，关于线段最短，我们有“两点之间，线段最短”，利用对称便可使问题得到解决．解析：如图4，作点D 关于AB 的对称点F ；点D 关于AC 的对称点G ， 连接FG ，交AB 于M ，交AC 于N ．∴D 、M 、N 即所求三个取样点．（请同学们试着证一证）．三、同类变式 例3 某班举行文艺晚会，桌子摆成两直条（如图５中的AO ，BO ），AO 桌面上摆满了糖果，BO 桌面上摆满了桔子，坐在C 处的学生小亮先拿糖果再拿桔子，然后回到座位，请你帮他设一条行走路线，使其所走的总路程最短？分析：此题是轴对称的特殊应用，需分两种情况讨论：①∠AOB 小于90°；②∠AOB 等于90°。

轴对称的作用用途有轴对称（也称为镜像对称）是指一个图形分别关于某条直线对称对折后，两部分重叠在一起，即左右对称。

轴对称的作用和用途在多个领域中具有重要意义，下面将详细介绍轴对称的作用和用途。

1. 几何学中的作用和用途：轴对称在几何学中具有重要的作用和用途。

例如，在做图形的复制、放大和缩小时，通过轴对称可以准确地绘制出图形的对称部分，从而保持图形的整体对称性。

对称的图形也常用于设计中，因为对称的图形给人以平衡、美观的感觉。

2. 艺术与设计中的作用和用途：在艺术与设计领域中，轴对称被广泛应用。

例如，在绘画和雕塑中，通过轴对称可以创造出平衡和和谐的效果，使作品更具有吸引力。

轴对称还可以用来设计装饰品、家具、建筑等，为其增加美感和艺术性。

同时，通过轴对称可以突出某些重要的元素，使设计更加突出。

3. 自然科学中的作用和用途：轴对称在自然科学中也有着广泛的应用。

例如，在生物学中，轴对称是生物体的一种常见形态，包括人类和许多其他动植物。

生物体的轴对称起到了平衡身体结构、提供运动和保护内部器官的作用。

轴对称也在晶体学中起到重要的作用，因为晶体的结构通常具有轴对称性，这是物质性质研究和应用的基础。

4. 计算机图形学中的作用和用途：在计算机图形学中，轴对称的概念被广泛运用于图像处理和计算机辅助设计等领域。

通过使用轴对称算法，可以实现图像的镜像反转、图像修复和图像特征提取等操作，提高图像处理和分析的效果。

轴对称还可以应用于3D模型的对称构建，减少模型的复杂度，并提高计算效率。

5. 数学中的作用和用途：轴对称是数学中一种重要的对称性质，具有广泛的应用。

在代数学和几何学中，轴对称的概念被广泛运用于研究对称性和变换等问题。

轴对称在线性代数、群论、微积分等数学分支中都有着重要的应用。

此外，轴对称还被应用于函数的分析和绘制中，例如，对称函数的图像在坐标系中具有轴对称性。

另外，轴对称还在解析几何学中有重要的应用，例如，通过轴对称可以推导出很多关于点、直线和曲线等的性质。

轴对称对称是一个十分宽广的概念，它出现在数学教材中，也存在于日常生活中，能在文学意境中感受它，也能在建筑物、绘画艺术、日常生活用品中看到它，更存在于大自然的深刻结构中．数学和人类文明同步发展，“对称”只是是纷繁数学文化中的标志之一．让我们来认识下轴对称在生活中的应用吧一、从轴对称图形中发现对称原理的运用根据轴对称图形的一半和对称轴可以精确的画出轴对称图形的另一半图形，这是在教学了轴对称图形后常见的习题。

在数学中，轴对称图形同时也为人们研究数学提供了某些启示，例如它在博弈问题中也常运用这一原理。

如：桌面上有21个棋子，排成一排，你一次可以拿一粒也可以拿两粒棋子，甚至可以拿三个棋子。

想拿哪里的棋子都行，不必按顺序拿，但拿两粒或三粒棋子时必须是相邻的即中间没有空隔或其他棋子，问：“两人轮流拿谁拿到最后一粒谁赢，你如果先拿能保证赢吗？”这题看上去挺复杂，按排列组合众多拿法要想一一分析清楚太费力，其实运用对称原理就非常简单，先拿的人只要先拿走中间一粒，即第十一粒棋，这样左、右两边各剩十粒，这样对方拿左边的棋子，你就拿右边的棋子，并且个数和位置和他对称，如果对方拿右边的棋子，你就按照他拿左边的棋子，总之只要保持左、右两边的棋子剩下的个数和位置一样，只要他有的拿，你也有的拿，因此最后一粒必然落入你手中，因此先拿必胜，如果棋子是20粒（偶数个），你就先拿中间的两粒，让左右两边各剩9粒棋子，这样你就必胜。

类似的题目还有如：用若干一元的硬币两人轮流将它摆在一个大圆盘上，要求硬币之间不能重叠，谁摆不下谁算输，是先摆赢还是后摆赢？显然根据对称原理，先摆的人只要先占住圆心，以后对方摆哪你就照他在对面对称着摆出，只要他有空间摆，那么在相对称的地方也必定有空间摆，直至对方摆不下为止，对方先输。

其实这两题的思维方法都来自轴对称图形的基本特征，教师在教学完轴对称图形的内容后可以适当的渗透这方面的知识，学生即乐于学习，又加深对轴对称图形知识的运用和深层理解，发现对称的美，感受到数学的魅力。

中心对称与轴对称的区别及应用对称在我们生活中是一个很常见的概念，可以说是几何学中最基础的概念之一。

在几何学中，对称主要分为两类，一类是中心对称，另一类是轴对称。

那么这两种对称的区别是什么呢？又有哪些应用呢？下面我们来一起探讨一下。

一、中心对称和轴对称的定义我们先来看一下中心对称的定义，“中心对称是指平面中存在一个点，经过这个点作图形内的任意一点与该点的连线，不随着这个内部点的位置而改变的变换。

”简单来说，就是图形被以一个点为中心，对称到对称轴的另一侧，而图形上的所有点到中心的距离相等。

接下来再来看轴对称的定义，“轴对称是指平面中存在一条直线，经过这条直线作图形内的任意点与该直线的连线，距离与垂线长不变的一种变换。

”也就是说轴对称是图形以一个轴线为对称轴，把图形对称到对称轴的另一侧，而对称轴上的点到对称轴的距离为0，其他点到对称轴的距离相等。

二、中心对称和轴对称的区别从定义上我们可以看出，中心对称和轴对称两者的主要区别在于基本元素不同，中心对称以点为基本元素，轴对称以直线为基本元素。

这也造成了二者性质和应用上的差异。

（1）性质的差异在性质上，我们可以看出，中心对称的对称轴是一条点，图形与其对称轴对应的位置称为中心对称位。

而轴对称的对称轴是一条直线，图形与其对称轴对应的位置称为轴对称位。

中心对称的变换具有对称性、可逆性和等距性。

但轴对称具有的三种性质都是对称性，但不具有可逆性和等距性。

（2）应用的差异在应用上，中心对称主要用于计算图形中心、判断图形重合和寻找图形的对应点。

而轴对称则广泛应用于建筑设计、机械加工、生物医学等领域。

例如，制作对称的模具、设计对称的装饰、轴射成像等。

三、结语中心对称和轴对称是几何学中最基本的概念之一，理解它们的区别和应用非常重要。

在实际应用中，根据需要选择相应的对称方式，可以更加方便和高效地进行工作。

我们希望通过这篇文章，更好的理解中心对称和轴对称，并为读者提供更多参考。

举例说明轴对称在现实生活中的应用。

举例说明轴对称在现实生活中的应用
轴对称是一种常见的几何概念，在现实生活中有广泛的应用。

以下是一些例子，说明了轴对称在不同领域中的实际应用。

工程设计
在工程设计中，轴对称被广泛应用于建筑设计、机械设计和电子设计等领域。

例如，在建筑设计中，对称的建筑设计可以让建筑物更加美观和稳固。

在机械设计中，轴对称的零件可以更容易地加工和装配。

在电子设计中，轴对称的电路布局可以提高电子设备的性能和可靠性。

自然科学
轴对称也在自然科学中有着广泛的应用。

在生物学中，许多生物体都具有轴对称的结构，如人类的身体、植物的叶子等。

在化学中，许多分子也具有轴对称的结构，这对于研究它们的性质和反应
机制具有重要意义。

在物理学中，轴对称的物体可以更容易地进行
力学和电磁学的分析。

艺术和设计
轴对称被广泛运用于艺术和设计领域。

许多艺术作品和设计作
品都使用了轴对称的构图，例如绘画、雕塑和建筑设计等。

轴对称
可以给人以平衡、和谐和美的感觉，使作品更加吸引人。

社会生活
在社会生活中，轴对称也有一定的应用。

例如，在家庭生活中，家具的布局可以使用轴对称的方式，使空间更加整洁和有序。

在社
会政治中，一些国家的旗帜和徽章设计也使用了轴对称的图案，代
表国家的统一和稳定。

总之，轴对称在现实生活中有广泛的应用，涵盖了工程设计、
自然科学、艺术和设计以及社会生活等多个领域。

通过利用轴对称，我们可以实现更美观、更高效、更稳定的设计和实践。