轴对称的应用

请简答轴对称原理的应用什么是轴对称原理？轴对称原理是指物体或系统在绕某个轴旋转180度后，仍然具有相同的形状和性质。

这个轴被称为轴对称轴。

轴对称原理是在理解和研究物体结构和性质时经常应用的原理之一。

在物理、化学和工程等领域中，轴对称原理有广泛的应用，可以帮助我们理解和解决各种问题。

轴对称原理的应用1.建筑设计轴对称原理在建筑设计中应用广泛。

建筑物的外立面、室内布局、建筑平面图和立面图等都常常采用轴对称的结构。

轴对称设计不仅能够实现美观和对称感，还有助于保持建筑结构的平衡和稳定性。

2.机械设计在机械设计中，轴对称原理被广泛应用于各种机械零件和设备的设计中。

例如，在设计齿轮、轴承和传动装置时，考虑到轴对称性可以减少噪音和振动，并提高零件的工作效率和寿命。

3.流体力学在流体力学中，轴对称原理被用于研究流体的行为和流动属性。

通过考虑轴对称性，可以简化流体力学问题的计算和分析。

例如，在设计管道系统和液压装置时，轴对称原理可以帮助工程师理解和优化流体的流动过程。

4.生物医学在生物医学领域，轴对称原理被用于理解和研究生物体的结构和功能。

例如，人体的左右对称性是基于轴对称原理的。

轴对称原理也可以应用于器官移植和组织修复等医学应用中。

5.光学设计在光学设计中，轴对称原理被用于设计光学元件和光学系统。

通过利用轴对称性，可以简化光学设计过程，并提高光学系统的性能和效率。

6.电路设计在电路设计中，轴对称原理被用于分析和优化电路的结构和特性。

例如，在设计电路板和电子设备时，考虑到轴对称性可以帮助工程师减少信号干扰和电路噪音，并提高电路的稳定性和可靠性。

总结轴对称原理是一种常用的原理，广泛应用于各个领域。

在建筑设计、机械设计、流体力学、生物医学、光学设计和电路设计等领域中，都可以看到轴对称原理的应用。

通过考虑和利用轴对称性，可以简化问题的分析和解决，提高设计和实施的效率和可靠性。

轴对称的应用例甲、乙两人轮流往一个圆桌面上放同样大小的硬币。

规则是：每人每次只能放一枚，硬币不许重叠，谁放完最后一枚硬币而使对方再也无处可放，谁就获胜。

如果甲先放，那么他怎样放才能取胜？分析与解：这道题初看太抽象，既不知道圆桌的大小，又不知道硬币的大小，谁知道该怎样放呀！我们用对称的思想来分析一下。

圆是关于圆心对称的图形，若A是圆内除圆心外的任意一点，则圆内一定有一点B与A关于圆心对称（见右图，其中AO=OB）。

所以，圆内除圆心外，任意一点都有一个（关于圆心的）对称点。

由此可以想到，只要甲把第一枚硬币放在圆桌面的圆心处，以后无论乙将硬币放在何处，甲一定能找到与之对称的点放置硬币。

也就是说，只要乙能放，甲就一定能放。

最后无处可放硬币的必是乙。

甲的获胜策略是：把第一枚硬币放到圆桌面的圆心处，以后总在乙上次放的硬币的对称点放置硬币。

这种利用对称思想的获胜策略体现出了一种机智，而这种机智来源于数学思想。

同学们经常进行这种锻炼，就会变得越来越聪明。

比如，有两堆火柴，第一堆20根，第二堆25根，甲、乙二人轮流从中取火柴，每次可以从任一堆中取走任意数量的火柴，取走最后一根火柴者胜。

甲先取，怎样才能保证获胜？利用对称的思想分析，只要甲先从第二堆中取走5根，此时两堆火柴的数量相等（也是一种对称），以后无论乙从哪一堆取多少根火柴，甲都对称地从另一堆取相同数量的火柴，只要乙能取，甲就能取，所以最后一根必被甲取走，甲胜。

练习：1、桌子上有8枚棋子，甲乙二人轮流拿棋子。

规定先拿的只要不都拿走，拿几枚都成，后拿者不能多于先拿的2倍，如此进行下去，谁拿最后一枚棋子谁就算胜利。

请你回答，怎样拿必然取胜，为什么？2、桌子上有两堆棋子，一堆8枚，一堆9枚，甲乙二人轮流拿棋子。

规定每次只能从一堆中拿，拿几枚都成，谁拿最后一枚棋子谁就算胜利。

请你回答，怎样拿必然取胜，为什么？。

轴对称图形轴对称图形是几何学中的一个重要概念，在许多领域中都有着广泛的应用。

轴对称图形是指可以通过某条虚拟线（称为轴）将图形分成两个对称的部分的图形。

接下来我们将深入探讨轴对称图形的性质、特点以及一些实际应用。

轴对称图形的性质轴对称图形具有以下几个显著的性质：1.对称轴：轴对称图形存在一个或多个对称轴，通过这些轴，可以将图形分成两个完全对称的部分。

对称轴可以是水平、垂直或斜线。

2.对应点：轴对称图形上的每个点都有一个对应的对称点，这个对称点关于对称轴相对位置相同，但是在轴对称图形中却是互为镜像的。

3.性质保持不变：轴对称变换不改变轴对称图形的性质，如面积、周长等，它只改变图形在空间中的位置和方向。

轴对称图形的分类根据轴对称的不同性质，轴对称图形可以分为以下几类：1.轴对称图形：最简单的轴对称图形是对称图形本身，例如正方形、正圆等。

2.轴对称字母：字母X在垂直中线上是轴对称。

3.轴对称数字：数字0、1、8在水平、垂直中线上是轴对称的。

4.轴对称图形的组合：多个轴对称图形可以组合在一起形成一个更大的轴对称图形。

轴对称图形的实际应用轴对称图形在日常生活中有着广泛的应用，下面列举几个实际应用：1.艺术创作：许多艺术作品中都运用了轴对称的原理，通过对称的布局或对称的图案来吸引观众的眼球。

2.建筑设计：建筑中的对称结构能够给人一种和谐、美感的感受。

许多古代建筑和现代建筑都运用了轴对称的设计。

3.产品设计：在产品设计中，轴对称设计能够提升产品的稳定性和美观性，例如汽车、手机等产品。

4.生物学：生物体中也存在轴对称结构，例如人体的左右对称、植物的对称花瓣等。

总结轴对称图形作为一种重要的几何概念，不仅在数学中有着丰富的性质和特点，而且在各个领域都有着重要的应用。

通过深入研究和理解轴对称图形，我们可以更好地利用这一概念在日常生活和工作中发挥作用，为人们创造更多美好的体验和设计。

希望本文对读者们有所启发，谢谢阅读！。

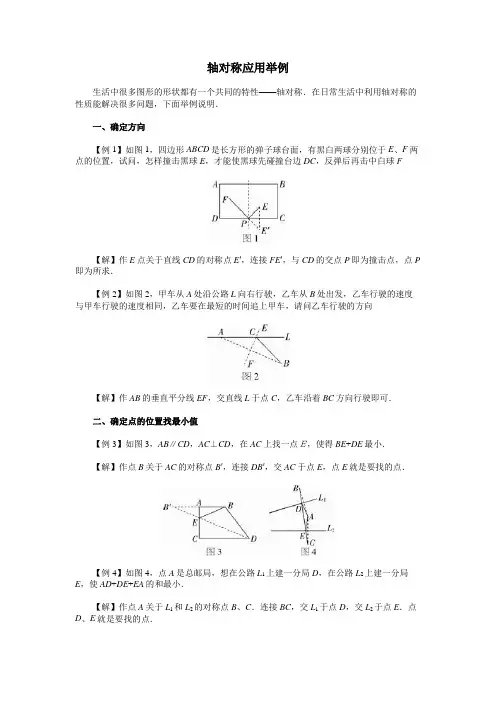
轴对称应用举例生活中很多图形的形状都有一个共同的特性——轴对称．在日常生活中利用轴对称的性质能解决很多问题，下面举例说明．一、确定方向【例1】如图1，四边形ABCD是长方形的弹子球台面，有黑白两球分别位于E、F两点的位置，试问，怎样撞击黑球E，才能使黑球先碰撞台边DC，反弹后再击中白球F【解】作E点关于直线CD的对称点E′，连接FE′，与CD的交点P即为撞击点，点P 即为所求．【例2】如图2，甲车从A处沿公路L向右行驶，乙车从B处出发，乙车行驶的速度与甲车行驶的速度相同，乙车要在最短的时间追上甲车，请问乙车行驶的方向【解】作AB的垂直平分线EF，交直线L于点C，乙车沿着BC方向行驶即可．二、确定点的位置找最小值【例3】如图3，AB∥CD，AC⊥CD，在AC上找一点Ｅ，使得BE+DE最小．【解】作点B关于AC的对称点B′，连接DB′，交AC于点E，点E就是要找的点．【例4】如图4，点A是总邮局，想在公路L1上建一分局D，在公路L2上建一分局E，使AD+DE+EA的和最小．【解】作点A关于L1和L2的对称点B、C．连接BC，交L1于点D，交L2于点E．点D、E就是要找的点．三、与其他学科结合唐朝某地建造了一座十佛寺，竣工时，太守在庙门右边写了一副上联“万瓦千砖百匠造成十佛寺”，望有人对出下联，且表达恰如其分，你能对出下联来吗对联中有数字万、千、百、十，几个月过去了，无人能对，有个文人李生路过，感觉庙前没有下联不像话，十分感慨．一连几天在庙前苦思冥想，未能对出下联，有次在庙前散步，望见一条大船由远而来，船夫正使劲的摇橹，这时李生突发灵感，对出了下联——“一舟二橹四人摇过八仙桥”．太守再次路过此庙时，看到下联，连连称赞“妙妙妙”．这副对联数字对数字，事物对事物，对称美如此的和谐．可见，对称美在文学方面也有生动深刻的体现．生活中的轴对称无处不在，只要你善于观察,将会发现其间所蕴涵的丰富的文化价值和对称美给人带来的回味无穷的享受．。

轴对称的作用用途有轴对称（也称为镜像对称）是指一个图形分别关于某条直线对称对折后，两部分重叠在一起，即左右对称。

轴对称的作用和用途在多个领域中具有重要意义，下面将详细介绍轴对称的作用和用途。

1. 几何学中的作用和用途：轴对称在几何学中具有重要的作用和用途。

例如，在做图形的复制、放大和缩小时，通过轴对称可以准确地绘制出图形的对称部分，从而保持图形的整体对称性。

对称的图形也常用于设计中，因为对称的图形给人以平衡、美观的感觉。

2. 艺术与设计中的作用和用途：在艺术与设计领域中，轴对称被广泛应用。

例如，在绘画和雕塑中，通过轴对称可以创造出平衡和和谐的效果，使作品更具有吸引力。

轴对称还可以用来设计装饰品、家具、建筑等，为其增加美感和艺术性。

同时，通过轴对称可以突出某些重要的元素，使设计更加突出。

3. 自然科学中的作用和用途：轴对称在自然科学中也有着广泛的应用。

例如，在生物学中，轴对称是生物体的一种常见形态，包括人类和许多其他动植物。

生物体的轴对称起到了平衡身体结构、提供运动和保护内部器官的作用。

轴对称也在晶体学中起到重要的作用，因为晶体的结构通常具有轴对称性，这是物质性质研究和应用的基础。

4. 计算机图形学中的作用和用途：在计算机图形学中，轴对称的概念被广泛运用于图像处理和计算机辅助设计等领域。

通过使用轴对称算法，可以实现图像的镜像反转、图像修复和图像特征提取等操作，提高图像处理和分析的效果。

轴对称还可以应用于3D模型的对称构建，减少模型的复杂度，并提高计算效率。

5. 数学中的作用和用途：轴对称是数学中一种重要的对称性质，具有广泛的应用。

在代数学和几何学中，轴对称的概念被广泛运用于研究对称性和变换等问题。

轴对称在线性代数、群论、微积分等数学分支中都有着重要的应用。

此外，轴对称还被应用于函数的分析和绘制中，例如，对称函数的图像在坐标系中具有轴对称性。

另外，轴对称还在解析几何学中有重要的应用，例如，通过轴对称可以推导出很多关于点、直线和曲线等的性质。

轴对称对称是一个十分宽广的概念，它出现在数学教材中，也存在于日常生活中，能在文学意境中感受它，也能在建筑物、绘画艺术、日常生活用品中看到它，更存在于大自然的深刻结构中．数学和人类文明同步发展，“对称”只是是纷繁数学文化中的标志之一．让我们来认识下轴对称在生活中的应用吧一、从轴对称图形中发现对称原理的运用根据轴对称图形的一半和对称轴可以精确的画出轴对称图形的另一半图形，这是在教学了轴对称图形后常见的习题。

在数学中，轴对称图形同时也为人们研究数学提供了某些启示，例如它在博弈问题中也常运用这一原理。

如：桌面上有21个棋子，排成一排，你一次可以拿一粒也可以拿两粒棋子，甚至可以拿三个棋子。

想拿哪里的棋子都行，不必按顺序拿，但拿两粒或三粒棋子时必须是相邻的即中间没有空隔或其他棋子，问：“两人轮流拿谁拿到最后一粒谁赢，你如果先拿能保证赢吗？”这题看上去挺复杂，按排列组合众多拿法要想一一分析清楚太费力，其实运用对称原理就非常简单，先拿的人只要先拿走中间一粒，即第十一粒棋，这样左、右两边各剩十粒，这样对方拿左边的棋子，你就拿右边的棋子，并且个数和位置和他对称，如果对方拿右边的棋子，你就按照他拿左边的棋子，总之只要保持左、右两边的棋子剩下的个数和位置一样，只要他有的拿，你也有的拿，因此最后一粒必然落入你手中，因此先拿必胜，如果棋子是20粒（偶数个），你就先拿中间的两粒，让左右两边各剩9粒棋子，这样你就必胜。

类似的题目还有如：用若干一元的硬币两人轮流将它摆在一个大圆盘上，要求硬币之间不能重叠，谁摆不下谁算输，是先摆赢还是后摆赢？显然根据对称原理，先摆的人只要先占住圆心，以后对方摆哪你就照他在对面对称着摆出，只要他有空间摆，那么在相对称的地方也必定有空间摆，直至对方摆不下为止，对方先输。

其实这两题的思维方法都来自轴对称图形的基本特征，教师在教学完轴对称图形的内容后可以适当的渗透这方面的知识，学生即乐于学习，又加深对轴对称图形知识的运用和深层理解，发现对称的美，感受到数学的魅力。

轴对称与中心对称初步轴对称和中心对称是几何学中常见的两种对称性，它们在平面和立体图形的研究中起着重要的作用。

本文将初步介绍轴对称和中心对称的概念、特点以及应用。

一、轴对称轴对称是指存在一条直线，将图形分成两部分，其中一部分关于该轴对称。

具有轴对称的图形左右对称，也称为镜像对称。

1. 概念与特点轴对称即轴对称图形，是指图形中存在一条轴线（称为轴对称线），使得这条轴线两侧的图形完全相同或镜像对称。

轴对称的图形可以是平面图形，也可以是立体图形。

轴对称图形的特点有：- 与轴对称线平行的直线上对应点的横坐标相等，纵坐标互为相反数；- 如果一点在轴对称线上，则它与轴对称线的距离为0；- 轴对称图形任意线段的中点都位于轴对称线上；- 轴对称图形的任意两个点关于轴对称线互为镜像，即从一个点经过轴对称线映射到另一个点。

2. 轴对称的应用- 建筑设计：许多建筑物利用轴对称设计，使得左右对称，给人以美感和协调感；- 摄影艺术：轴对称构图常常被摄影师用于创作，使得画面更加平衡和稳定；- 数学问题：轴对称用于解决一些几何问题，如寻找对称中心等。

二、中心对称中心对称是指存在一个点，将图形中任意一点与该中心对称，使得图形两侧完全相同或镜像对称。

具有中心对称的图形具有圆周对称性。

1. 概念与特点中心对称即中心对称图形，是指图形中存在一个点（称为中心对称点），使得图形中任意一点关于中心对称点对称。

中心对称的图形可以是平面图形，也可以是立体图形。

中心对称图形的特点有：- 中心对称图形上任意两点关于中心对称点互为镜像，即从一个点经过中心对称映射到另一个点；- 中心对称图形上任意线段的中点都位于中心对称点上；- 中心对称图形上的任意点关于中心对称点的距离相等。

2. 中心对称的应用- 艺术设计：许多艺术品如画作、图案等利用中心对称设计，给观者以和谐、平衡的美感；- 生物结构：许多生物的结构具有中心对称性，如蝴蝶的翅膀、花朵的组织等；- 数学模型：中心对称性常常用于数学模型的描述和分析，如圆和球等。

轴对称是几何形状的一种特殊属性，简单来说，轴对称就是形状能够在条直线上镜像对称。

在数学中，轴对称的性质可以用来解决各种几何问题，例如确定形状的对称中心、计算对称线的方程、推断特定的性质等等。

在本篇文章中，我将为您解释轴对称的定义和公式，并且提供一些重要的定理和应用。

希望这些信息能帮助您更好地理解轴对称的概念。

一.轴对称的定义和性质1.轴对称的定义：一个图形或物体如果可以围绕一个轴旋转180度，并且旋转后的图形和原来的图形完全重合，那么这个图形或物体就是轴对称的。

这个轴称为轴对称的轴线或中轴线。

2.轴对称的图形：轴对称的图形是一种两边镜像对称的图形，在轴对称图形中，可以找到一个中心轴称为中轴线，物体或图形的任意一个点关于轴线对称的点也在轴上。

3.轴对称的性质：-轴对称的图形在中轴线两侧的点关于中轴线上的点是镜像对称的。

-轴对称的图形的两边在中轴线上的对应点距离相等。

-轴对称的图形可以由一个部分沿着中轴线复制后叠加而成。

二.轴对称的公式和特征1.轴对称的方程：一般来说，轴对称的方程可以用以下形式表示：-对于直线轴对称：y=k或x=k（k为常数）-对于曲线轴对称：x=f(y)或y=f(x)（f表示一个函数）2.轴对称的特征：-函数关系：轴对称的图形通常可以表示为一个函数关系的图形，例如，y=x^2是一个轴对称的抛物线。

-对称点：轴对称的图形中，图形上每个点关于中轴线都有一个对称的点。

-轴对称线的特征：轴对称的图形中，中轴线上的每一点都是图形的对称点，也就是说，如果(x,y)是图形上的一点，那么(-x,y)也是图形上的一点。

三.轴对称的定理和应用1.轴对称的定理：-对称中心定理：一个图形如果轴对称，那么图形上的任意两个点关于对称中心对称。

-垂直线对称：轴对称图形以垂直线为对称轴进行对称。

-水平线对称：轴对称图形以水平线为对称轴进行对称。

-原点对称：轴对称图形以原点为对称中心进行对称。

2.轴对称的应用：-计算对称轴的方程：通过已知的对称点和对称中心，可以计算出轴对称的方程。

D轴对称图形性质的实际应用美丽、和谐的轴对称图形随处可见，轴对称图形具有很多重要的性质，在数学解题中，若能对其性质加以巧妙运用，则可以使问题的解决变得非常简单．一、求角的度数例1 如图1，六边形ABCDEF 是轴对称图形，CF ∠BCF=150°，则∠AFE+∠BCD 的大小是（ ）． （Ａ）150° （Ｂ）300° （Ｃ）210° （Ｄ）330° 析解：因为六边形ABCDEF 是轴对称图形，CF 所在的直线是它的对称轴，根据轴对称图形性质可知∠AFC=∠EFC ，∠BCF=∠DCF .而∠AFE+∠BCD=∠AFC+∠EFC+∠BCF+∠DCF=2∠AFC+2∠BCF= 2（∠AFC+∠BCF ）=300°，故应选Ｂ．二、求三角形周长 例2 如图2，Rt △ABC 中，∠B ＝90°，AB ＝3厘米，BC ＝4C 与A 重合，得折痕DE ，则△ABE 的周长等于____厘米.析解：因为△CDE 折叠后与△ADE 重合，所以△AEC 是以 折痕DE 为对称轴的轴对称图形，因此AE=EC.所以△ABE 的周长=AB+AE+BE=AB+EC+BE=AB+AC=3厘米+4厘米=7厘米.例3．如图３,在△ＡＢＣ中,AB=AC ，∠A=40︒,AB 的垂直平分线MN 交AC 于点D ，BC=5厘米．求：（1）∠DBC 的度数;（2）如△DBC 的周长为14厘米,求AB 的长.析解：(1)因为AB=AC,所以∠ABC=∠C,∠A=40, ∠ABC=180402︒-︒=70︒.因为MN 是AB 的垂直 平分线,所以DA=DB,所以∠DBA=40︒.所以∠DBC=70︒-40︒=30︒. (2) △DBC 的周长=BD+DC+BC+=DA+DC+BC=AC+BC.因为△DCB 的周长14厘米,BC=5厘米,所以AC=14-5=9厘米.所以AB=9厘米.。

几何中的轴对称与旋转对称几何学是数学的一个分支，研究与形状、大小、相对位置以及它们的属性有关的问题。

在几何学中，轴对称和旋转对称是两个常见的概念，它们在描述图形的对称性方面起着重要的作用。

一、轴对称轴对称，也称为镜像对称，是指一个图形在某条直线轴上的两侧完全对称。

这条直线轴称为轴线或镜面。

轴对称经常出现在各种几何图形中，比如点、线、多边形和曲线等。

轴对称的关键特点是图形的每一部分都与轴线上的相应部分对称。

如果通过折叠沿着轴线将图形的两侧重合，每一对对称部分都能完全重合在一起。

例如，正方形和圆都是轴对称图形。

轴对称在几何学中有许多实际应用，例如在建筑设计中，设计师常常运用轴对称的原理，通过将图形沿轴线进行对称排列，使得建筑更加平衡美观。

另外，轴对称也广泛应用于绘画、雕塑和纹样设计等领域。

二、旋转对称旋转对称是指一个图形能够围绕着某个中心点进行旋转，使得旋转后的图形与原图形完全重合。

这个中心点称为旋转中心，旋转对称的角度称为旋转角度。

旋转对称的特点是图形的每一部分都以旋转中心为中心进行旋转，并且旋转后与原图形相重合。

例如，正五边形和等边三角形都是旋转对称图形。

旋转对称在几何学中也有广泛的应用。

在自然界中，许多有机体，如花朵、螺旋壳等都存在旋转对称。

在艺术设计中，旋转对称也被广泛应用于图案的设计和装饰。

三、轴对称与旋转对称的关系轴对称和旋转对称是紧密相关的。

轴对称图形可以看做是以轴线为旋转中心进行旋转对称后得到的图形。

而旋转对称图形则可以通过将图形沿轴线进行轴对称操作来得到。

这种关系也可以通过一些例子来说明。

例如，在圆上每一点都可以作为旋转中心，使得圆能够旋转对称。

而当旋转中心位于圆心时，旋转对称的角度为360度，此时圆既是旋转对称图形，也是轴对称图形。

再例如，正方形具有4个轴对称和4个旋转对称。

其中每条对角线都是轴对称线，而以正方形的中心为旋转中心旋转90度、180度和270度，可以得到与原图形完全重合的图形。

认识轴对称知识点总结一、轴对称的定义轴对称是指一个几何图形相对于某条轴线对称，即图形的两侧关于轴线对称。

轴对称是一种基本的几何变换，它可以帮助我们理解和研究各种几何图形的性质，解决与几何图形相关的问题。

二、轴对称的性质1. 被轴对称的图形的对称轴上的点不动，对称轴的垂线上的点互为对称点。

2. 被轴对称的图形的对称轴上任意两点的对称点都在对称轴上。

3. 被轴对称的图形上的任意一点，与其对称点关于对称轴的距离相等。

三、轴对称的应用轴对称在几何学中有着广泛的应用。

在平面几何中，我们经常通过轴对称来研究图形的性质、判断图形的对称特征、构造具有对称性的图形等。

在日常生活中，轴对称也有很多实际的应用，比如建筑设计、工艺品制作、装饰设计等。

四、轴对称的判定方法1. 通过观察图形的性质来判断是否具有轴对称性。

2. 通过观察图形的对称性来判断是否具有轴对称性。

3. 通过对称图形的性质和定理来判断是否具有轴对称性。

五、轴对称的性质及定理1. 轴对称的图形的对称轴上的点不动定理：轴对称的图形的对称轴上的点不动，即对称轴上的任意一点都是自身的对称点。

2. 轴对称的图形的对称轴是垂直的定理：如果一个图形具有轴对称性，那么图形的对称轴一定是垂直的。

3. 被轴对称的图形的对称轴上任意两点的对称点都在对称轴上定理：对任意一点A在对称轴上，A的对称点B也在对称轴上。

4. 对称中心位置可以通过对称图形的性质来判断定理：对称中心位置是轴对称的图形的重要性质之一。

5. 被轴对称的图形上的任意一点，与其对称点关于对称轴的距离相等定理：被轴对称的图形上的任意一点，与其对称点关于对称轴的距禿相等。

六、轴对称的图形1. 线段线段是具有轴对称性的图形。

2. 三角形三角形也可以是轴对称的图形。

3. 正方形和矩形正方形和矩形也是轴对称的图形。

4. 圆形圆形也具有轴对称性。

七、轴对称的构造1. 利用尺规作图的方法来构造轴对称的图形。

2. 利用计算机绘图软件来构造轴对称的图形。

学习指导２０２４年１月下半月㊀㊀㊀例谈轴对称性质的应用◉贵州省威宁县第十一中学㊀王光杰㊀㊀轴对称属于全等变换,对称轴两旁的部分是全等的,据此,可以推出关于轴对称的诸多性质,如 对称点的连线被对称轴垂直平分 对应线段相等,对应角相等 对称点与对称轴上任一点连线的夹角被对称轴平分 等．只有明确这些性质,知道其应用于哪一方面,才能在中考中稳操胜券．１用 对称点的连线段被对称轴垂直平分 求线段长㊀㊀由于在对称轴两侧的部分能够互相重合,因此,当对称点连线后,两对称点到交点的距离相等,对称点的连线被对称轴垂直平分．图１例１㊀如图１,已知点M是øA O B内任意一点,点M１,M关于O A对称,点M２,M关于O B对称,连结M１M２,分别交O A,O B于C,D两点,连接M C,M D,若M１M２＝１０c m,求әM C D的周长．分析:根据轴对称图形的性质,即 对称点的连线被对称轴垂直平分 ,可得O A垂直平分MM１,O B垂直平分MM２．依据 线段垂直平分线上的点到线段两个端点的距离相等 ,可得M C＝M１C,MD＝M２D．于是әM C D的周长就转化为线段M１M２的长．理由如下．由点M１,M关于O A对称,可知O A垂直平分M１M,则M C＝M１C．同理,MD＝M２D．所以әM C D的周长为M C＋C D＋M D＝M１C＋C D＋M２D＝M１M２＝１０c m．点评:此题的图形也是下面问题的作图方法,即在已知角内有一点M,在角的两边上求作两个点,使点M与这两点构成的三角形周长最小．图２变式练习１㊀如图２,点P是øA O B外一点,点M,N分别是øA O B两边上的点,点P关于O A的对称点Q恰好落在线段MN上,点P关于O B的对称点R落在线段MN的延长线上．若P M＝２．５c m,P N＝３c m,MN＝４c m,求线段Q R的长．答案:４．５c m．２用 对称点的连线段被对称轴垂直平分 求角度㊀㊀轴对称的性质有多种应用,不仅能求得图形中线段的长,而且可以求得角度,还可以用于证明．图３例２㊀如图３,在әA B C中,直线l交A B于点M,交B C于点N,点B关于直线l的对称点D在线段B C上,且A DʅMD,øB＝２８ʎ,求øD A B的度数．分析:因为点B关于直线l的对称点是点D,根据对称点的连线被对称轴垂直平分,得直线l是线段D B的垂直平分线,所以MD＝M B．根据等边对等角,得øMD B＝øB＝２８ʎ．根据三角形外角的性质,得øAMD＝øMD B＋øB＝５６ʎ．在R tәA DM中,根据三角形内角和定理,得øD A B＝９０ʎ－５６ʎ＝３４ʎ．点评:利用 对称点的连线被对称轴垂直平分 这一线段垂直平分线的性质,得到等腰三角形,自然就有等角了．图４变式练习２㊀如图４,在әA B C中,øA C B＝９０ʎ,A C＝B C,E为外角øBC D平分线上一动点(不与点C重合),点E关于直线B C的对称点为F,连接B E,连接A F并延长交直线B E于点G．(１)求证:A F＝B E．(２)用等式表示线段F G,E G与C E的数量关系,并证明．答案:(１)略;(２)G E２＋G F２＝２C E２．３用 对应线段相等,对应角相等 求线段长对应线段相等,对应角相等 是轴对称最基本的性质,在折叠问题中这个性质的应用最多．下面就是利用此性质解答的折叠问题．例３㊀如图５所示,A D是әA B C的中线,øA D C＝６０ʎ,把әA D C沿直线A D折过来,点C落在点Cᶄ的位置．６５２０２４年１月下半月㊀学习指导㊀㊀㊀㊀图５(１)在图中找出点C ᶄ,连接B C ᶄ;(２)如果B C ＝４,求B C ᶄ的长．分析:我们知道,翻折前后图６的两个图形关于折痕成轴对称图形,点C 与C ᶄ是对称点,所以可以用 作垂线 截相等 描点 的方法作出点C ᶄ(如图６);根据成轴对称的两个图形中对应线段相等,对应角相等 ,可得D C ᶄ＝D C ＝B D＝２,øC ᶄD A ＝øC D A ＝６０ʎ,从而得到等边三角形C ᶄB D ．(１)作C O ʅA D 并延长C O 至点C ᶄ,使O C ＝O C ᶄ,点C ᶄ即为所求．(２)连接C ᶄD ,则C D ＝C ᶄD ,øA D C ＝øA D C ᶄ＝６０ʎ,所以øB D C ᶄ＝６０ʎ．由B D ＝D C ＝２,可得B D ＝C ᶄD ＝２,则øC ᶄB D ＝øB C ᶄD ＝６０ʎ,可知әC ᶄB D 为等边三角形,所以B C ᶄ＝B D ＝２．点评:因为轴对称图形中 对应线段相等,对应角相等 ,所以图形折叠后与中线相结合,可得到等腰三角形,而等腰三角形是初中学习的重要图形,有关它的性质比较多．例４㊀如图７Ｇ１,әA B C 的点C 与C ᶄ关于A B 对称,点B 与B ᶄ关于A C 对称,连接B B ᶄ,C C ᶄ,交于点O ．图７Ｇ１㊀㊀㊀㊀㊀㊀㊀㊀㊀图７Ｇ２㊀㊀(１)如图７Ｇ１,若øB A C ＝３０ʎ,①求øB ᶄA C ᶄ的度数;②观察并描述:әA B C ᶄ可以由әA B ᶄC 通过什么变换得来?求出øB O C ᶄ的角度．(２)如图７Ｇ２,若øB A C ＝α,点D ,E 分别在A B ,A C 上,且C ᶄD ʊBC ʊB ᶄE ,B E ,CD 交于点F ,设øB F D ＝β,试探索α与β之间的数量关系,并说明理由．分析:(１)①因为点C ,C ᶄ关于A B 对称,点B ,B ᶄ关于A C 对称,由 对应线段相等,对应角相等 ,得øC A B ＝øB A C ᶄ＝øC A B ᶄ＝３０ʎ,所以øB ᶄA C ᶄ＝９０ʎ．②图７Ｇ１中,设A C 交B B ᶄ于点J ．әA B C ᶄ可以由әA B ᶄC 绕点A 顺时针旋转６０ʎ得到．因为A C ＝A C ᶄ,A B ＝A B ᶄ,øC A C ᶄ＝øB A B ᶄ＝６０ʎ,所以øA B ᶄO ＝øA C O ＝６０ʎ．因为øA J B ᶄ＝øO J C ,所以øB ᶄO C ＝øB ᶄA J ＝３０ʎ．故øB O C ᶄ＝３０ʎ．(２)β＝２α．理由:由轴对称的性质,得B C ＝B C ᶄ,D C ᶄ＝D C ,øA B C ᶄ＝øA B C ．因为D C ᶄʊB C ,由 两直线平行,内错角相等 ,得øC ᶄD B ＝øA B C ＝øC ᶄB D ,由等角对等边,得C ᶄD ＝C ᶄB ,所以B C ＝B C ᶄ＝C ᶄD ＝D C ．根据四边相等的四边形是菱形,得四边形B C D C ᶄ是菱形,所以C D ʊB C ᶄ．同理B E ʊC B ᶄ．所以øF C B ＋øC B C ᶄ＝１８０ʎ,即øF C B ＋２øA B C ＝１８０ʎ．同理øF B C ＋２øA C B ＝１８０ʎ,也即øB F D ＝øF B C ＋øF C B ,所以øD F B ＝１８０ʎ－２øA B C ＋１８０ʎ－２øA C B ＝３６０ʎ－２(øA B C ＋øA C B )＝２øB A C ．所以β＝２α．４用对称点与对称轴上任一点连线的夹角被对称轴平分 求角度或周长㊀㊀轴对称的 对称点与对称轴上任一点连线的夹角被对称轴平分 这一性质不经常用,常用在探究性质的问题中．图８例５㊀如图８,әA B C 与әA ᶄB ᶄC ᶄ关于直线MN 对称,әA ᶄB ᶄC ᶄ和әA ᵡB ᵡC ᵡ关于直线E F 对称,直线MN 与E F 交于点O ,试探究øB O B ᵡ与直线MN ,E F 所夹锐角α的数量关系．分析:连接O B ᶄ,O B ᵡ,O B ,根据 对称点与对称轴上任一点连线的夹角被对称轴平分 ,可得两组相等的角,即øM O B ＝øM O B ᶄ,øF O B ᶄ＝øF O B ᵡ,据此可得øB O B ᵡ＝２øM O B ᶄ＋２øF O B ᶄ＝２(øM O B ᶄ＋øF O B ᶄ)＝２øM O F ＝２α．点评:此题也反映出轴对称与旋转的关系,即当两条对称轴相交时,两次轴对称相当于一次绕着交点图９旋转对称轴夹角的２倍度数．变式练习３㊀如图９,点P在øA O B 的内部,点C 和点P 关于O A 对称,点P 关于O B 对称的点是D ,连接C D 交O A 于点M ,交O B 于点N ．(１)①若øA O B ＝６０ʎ,则øC O D ＝ʎ;②若øA O B ＝α,求øC O D 的度数．(２)若C D ＝４,则әP MN 的周长为．答案:(１)①１２０;㊀②２α．㊀(２)４．轴对称是图形变换之一,属于全等变换,是中考的必考内容,它常与其他图形结合起来考查,要求学生会运用运动的观点看问题．Z７５。