浅谈轴对称图形的简单应用

轴对称图形的定义和作用
轴对称图形概念
在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，并且对称轴用点画线表示；例如：等腰三角形、正方形、等边三角形、等腰梯形和圆和正多边形都是轴对称图形。

圆有无数条对称轴，都是经过圆心的直线。

要特别注意的是线段，它有两条对称轴，一条是这条线段所在的直线，另一条是这条线段的中垂线。

生活中轴对称图形
1.学习用品：笔、普通橡皮、铅笔盒等。

2.生活用品：桌子、椅子、床、眼镜、玻璃杯、炒锅等。

3.交通：车轮、火箭等。

4.建筑：天安门、英雄纪念碑等。

5.其他：太阳、月亮、地球等。

轴对称作用
1.为了美观，比如天安门的建筑，对称就显的美观漂亮。

2.保持平衡，比如飞机的两翼。

3.特殊工作的需要，比如五角星，剪纸。

4.可以利用轴对称估测一些东西的数据。

生活中有哪些轴对称现象
生活中，我们经常会遇到一些轴对称的现象，这些现象在日常生活中无处不在。

轴对称是指物体在某个轴线上的对称性，即物体的一部分关于这个轴线对称于另一部分。

让我们一起来看看生活中有哪些轴对称的现象吧。

首先，我们可以看到很多自然界中的轴对称现象。

比如，许多植物的叶子都具
有轴对称的特点，叶子的左半部分和右半部分关于中间的中脉对称。

这种轴对称的设计让植物在生长过程中更加稳定和美观。

其次，建筑物中也常常可以看到轴对称的设计。

许多古代建筑和现代建筑都采
用了轴对称的设计理念，比如对称的门窗、楼梯和装饰图案等。

这种设计不仅能够增加建筑物的美感，还能够在视觉上给人一种平衡和稳定的感觉。

除此之外，我们在日常生活中还可以看到许多轴对称的艺术作品。

比如对称的
花瓶、对称的家具、对称的服装等等。

这些设计不仅能够给人以美的享受，还能够在一定程度上提高生活品质。

总的来说，轴对称现象在生活中是无处不在的。

无论是自然界中的植物、建筑
物中的设计，还是艺术作品中的表现，轴对称都是一种美的体现。

让我们在日常生活中多留意这些轴对称的现象，感受到它们给我们带来的美好。

浅谈轴对称图形的应用养龙司中学——李明在数学的大家庭中。

有一对兄弟深深的吸引了我，他们的形状，他们的关系，他们的普遍性，让人觉得他们一直在我们的身边，离我们很近很近。

他们就是轴对称图形。

轴对称图形是一个一定要沿着某直线折叠后，直线两旁的部分互相重合的图形，之所以说到他们的关系是因为他们两个总是被一条直线所连着，好似一对分不开的兄弟，关系十分的密切。

把他们拉在一起的这条直线就是他们的对称轴。

当然这条对称轴就像一个公正的法官。

左右两边的长度、面积、大小等，都一点儿也不差，唯一不同的就是他们所朝的方向。

在数学的课本上，我们看见过他们的身影，我们也接触和了解过他们。

但是他们给我印象更多的，却是他们在日常生活中所扮演、组成的图形或者可以说是事物。

一、生活当中的轴对称图形1、自然界中的轴对称图形当我漫步在街头时，我时常看见飞来飞去的蝴蝶。

当一只蝴蝶停留在花朵上，张合着翅膀时，我发现如果将蝴蝶两只触角的中点与尾部相连接，连接好的线段所在的那一条直线就是其对称轴。

而右边的翅膀就像是左边的翅膀沿着对称轴翻过去的图形。

跟蝴蝶一样是轴对称图形的动物还有很多。

比如蜻蜓、飞蛾等。

如果到了秋天，远看稻田，金黄的一片，不禁使人感觉到又是一个丰收的季节。

就在这个令人喜悦的季节里，我行走在田边的小路上，随手捡起了一片金黄的树叶，仔细的观察了一下，发现其实树叶也有对称轴。

如果我们将树叶中间的那根经，当成是其左右两边的对称轴，那将树叶右边部分沿着这条对称轴对折过去，正好与左边的一半树叶重合。

2、商标中的轴对称图形有一次，我跟我的家人去中国银行取钱，我无意间发现中国银行的标志也是一个轴对称图形。

这个图形的对称轴有两条。

第一条是图标中两竖相连接所形成的，而另一条就是方框上下两条横线连接的线段的中点，所在的那一条直线就是其第二条对称轴。

和中国银行一样的还有中国联通、中国农业银行以及奔驰汽车等轴对称图形。

但是如果大家觉得前面几个例子，平时都没有注意到的话，那么下面说到的这个例子大家肯定熟悉的不得了。

2023-11-06•轴对称的定义与性质•生活中的轴对称•轴对称在设计中的应用目录•轴对称的计算机实现•总结与展望01轴对称的定义与性质轴对称是指一个物体关于某一直线（称其为对称轴）对称，也就是说，物体在对称轴的两侧是镜像对称的。

在几何学中，轴对称是一种基本的对称形式，它反映了物体的空间位置关系。

轴对称性是一种等价关系，即如果一个图形关于某一直线对称，则它具有一些特殊的性质。

例如，对于一个关于y轴对称的图形，其关于y轴的垂线是对称的。

轴对称的应用在日常生活中，轴对称的应用非常广泛。

例如，在建筑设计中，许多建筑物都利用了轴对称的概念来设计它们的外观和内部布局。

在自然界中，许多物体也具有轴对称性，例如雪花、蝴蝶翅膀等。

02生活中的轴对称建筑中的轴对称故宫01故宫是中国著名的古建筑群，其主体建筑群具有明显的轴对称特点，从午门到神武门，左右两边的建筑完全对称，体现了中国古代建筑的和谐之美。

雅典卫城02希腊雅典卫城是欧洲最古老、最杰出的古建筑之一，其建筑风格具有典型的轴对称特点，尤其是卫城的中心建筑帕台农神庙，其布局与周围的建筑群呈轴对称。

印度泰姬陵03泰姬陵是印度最著名的古建筑之一，也是世界遗产之列。

它以完美的轴对称和精湛的白色大理石雕刻技术而闻名于世。

雕塑雕塑作品也经常利用轴对称来表现形式美。

例如，古希腊雕塑家经常使用轴对称来创作人体雕塑，以表现人体的平衡和和谐。

绘画在绘画中，轴对称经常被用来创造和谐、平衡和稳定的感觉。

例如，在肖像画中，人物的脸部特征通常会以鼻子为中心，左右两边对称分布。

音乐在音乐中，轴对称也被广泛运用。

例如，在交响乐中，乐章之间往往会有明显的轴对称结构，以表现音乐的形式美和平衡感。

艺术中的轴对称蝴蝶的翅膀通常是轴对称的，这种对称性不仅使蝴蝶看起来更加美观，还帮助它们在飞行时保持平衡和稳定。

自然界中的轴对称蝴蝶雪花是自然界中最具代表性的轴对称物体之一。

每个雪花都有六个分支，每个分支都呈现出完美的轴对称形态。

轴对称是指一个图形或物体经过一条轴后两边对称。

轴对称的性质在生活中有许多应用。

1.在建筑设计中，轴对称的图形经常被用来设计建筑物的外观。

这种设计方式能使建筑物看起来整洁、美观、平衡。

2.在平面设计中，轴对称的图形常用于制作海报、海报、宣传单等。

这种设计方式能使设计看起来美观、平衡、有序。

3.在产品设计中，轴对称的图形常用于设计产品的外观。

这种设计方式能使产品看起来美观、平衡、有序。

4.在艺术设计中，轴对称的图形常用于设计艺术作品的构图。

这种设计方式能使艺术作品看起来美观、平衡、有序。

轴对称图形轴对称图形是几何学中的一个重要概念，在许多领域中都有着广泛的应用。

轴对称图形是指可以通过某条虚拟线（称为轴）将图形分成两个对称的部分的图形。

接下来我们将深入探讨轴对称图形的性质、特点以及一些实际应用。

轴对称图形的性质轴对称图形具有以下几个显著的性质：1.对称轴：轴对称图形存在一个或多个对称轴，通过这些轴，可以将图形分成两个完全对称的部分。

对称轴可以是水平、垂直或斜线。

2.对应点：轴对称图形上的每个点都有一个对应的对称点，这个对称点关于对称轴相对位置相同，但是在轴对称图形中却是互为镜像的。

3.性质保持不变：轴对称变换不改变轴对称图形的性质，如面积、周长等，它只改变图形在空间中的位置和方向。

轴对称图形的分类根据轴对称的不同性质，轴对称图形可以分为以下几类：1.轴对称图形：最简单的轴对称图形是对称图形本身，例如正方形、正圆等。

2.轴对称字母：字母X在垂直中线上是轴对称。

3.轴对称数字：数字0、1、8在水平、垂直中线上是轴对称的。

4.轴对称图形的组合：多个轴对称图形可以组合在一起形成一个更大的轴对称图形。

轴对称图形的实际应用轴对称图形在日常生活中有着广泛的应用，下面列举几个实际应用：1.艺术创作：许多艺术作品中都运用了轴对称的原理，通过对称的布局或对称的图案来吸引观众的眼球。

2.建筑设计：建筑中的对称结构能够给人一种和谐、美感的感受。

许多古代建筑和现代建筑都运用了轴对称的设计。

3.产品设计：在产品设计中，轴对称设计能够提升产品的稳定性和美观性，例如汽车、手机等产品。

4.生物学：生物体中也存在轴对称结构，例如人体的左右对称、植物的对称花瓣等。

总结轴对称图形作为一种重要的几何概念，不仅在数学中有着丰富的性质和特点，而且在各个领域都有着重要的应用。

通过深入研究和理解轴对称图形，我们可以更好地利用这一概念在日常生活和工作中发挥作用，为人们创造更多美好的体验和设计。

希望本文对读者们有所启发，谢谢阅读！。

对称图形的应用如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴。

对称轴绝对是一条直线。

圆是轴对称图形，直径所在的直线是圆的对称轴，圆有无数条对称轴。

在同圆或等圆里，直径的长度是半径的2倍，可以表示为d=2r或r=d。

一.生活中的轴对称1.自然界中的轴对称当我漫步在街头时，我时常看见飞来飞去的蝴蝶。

当一只蝴蝶停留在花朵上，张合着翅膀时，我发现如果将蝴蝶两只触角的中点与尾部相连接，连接好的线段所在的那一条直线就是其对称轴。

而右边的翅膀就像是左边的翅膀沿着对称轴翻过去的图形。

跟蝴蝶一样轴对称的生物还有很多。

比如随意从地上捡起的树叶，仔细观察你会发现它也是轴对称的。

如果我们将树叶中间的那根经，当成是其左右两边的对称轴，那将树叶右边部分沿着这条对称轴对折过去，正好与左边的一半树叶重合。

2.商标中的轴对称在无意间，你可以发现很多商标也同样是轴对称的，有家喻户晓的麦当劳，各种银行，各种汽车的标志都是轴对称的。

但是如果大家觉得前面几个例子，平时都没有注意到的话，那么下面说到的这个例子大家肯定熟悉的不得了。

这个例子就是商标，我先来举一个吧。

平时我最大的兴趣就是吃零食。

所以我对“旺旺”这个商标熟悉的不得了。

我发现在旺旺这个商标当中，将其头发上的一个中点到两脚脚后跟之间的线段的中点，想连接的线段所在的那一条直线就是其对称轴。

也正是这条对称轴将旺旺这个图标分成了相等的两份。

像旺旺这样具有对称轴的商标还有很多。

二、文学当中的轴对称1、文字中的轴对称图形众人皆知，中国经过了上下五千年历史的熏陶。

其轴对称形状的字也是数不胜数。

比如“西”、“内”、“具”、“里”还有许多剪纸作品，也正是因为有了轴对称的存在，使其更加精致、美观。

其实有时候，对称轴也具有复制的功能，它能够把一个字，分成与其相同的两个字，像“二”如果把它的对称轴当作是第一横的中点和第二横的中点，所连接成的线段所在的直线的话。

轴对称对称是一个十分宽广的概念，它出现在数学教材中，也存在于日常生活中，能在文学意境中感受它，也能在建筑物、绘画艺术、日常生活用品中看到它，更存在于大自然的深刻结构中．数学和人类文明同步发展，“对称”只是是纷繁数学文化中的标志之一．让我们来认识下轴对称在生活中的应用吧一、从轴对称图形中发现对称原理的运用根据轴对称图形的一半和对称轴可以精确的画出轴对称图形的另一半图形，这是在教学了轴对称图形后常见的习题。

在数学中，轴对称图形同时也为人们研究数学提供了某些启示，例如它在博弈问题中也常运用这一原理。

如：桌面上有21个棋子，排成一排，你一次可以拿一粒也可以拿两粒棋子，甚至可以拿三个棋子。

想拿哪里的棋子都行，不必按顺序拿，但拿两粒或三粒棋子时必须是相邻的即中间没有空隔或其他棋子，问：“两人轮流拿谁拿到最后一粒谁赢，你如果先拿能保证赢吗？”这题看上去挺复杂，按排列组合众多拿法要想一一分析清楚太费力，其实运用对称原理就非常简单，先拿的人只要先拿走中间一粒，即第十一粒棋，这样左、右两边各剩十粒，这样对方拿左边的棋子，你就拿右边的棋子，并且个数和位置和他对称，如果对方拿右边的棋子，你就按照他拿左边的棋子，总之只要保持左、右两边的棋子剩下的个数和位置一样，只要他有的拿，你也有的拿，因此最后一粒必然落入你手中，因此先拿必胜，如果棋子是20粒（偶数个），你就先拿中间的两粒，让左右两边各剩9粒棋子，这样你就必胜。

类似的题目还有如：用若干一元的硬币两人轮流将它摆在一个大圆盘上，要求硬币之间不能重叠，谁摆不下谁算输，是先摆赢还是后摆赢？显然根据对称原理，先摆的人只要先占住圆心，以后对方摆哪你就照他在对面对称着摆出，只要他有空间摆，那么在相对称的地方也必定有空间摆，直至对方摆不下为止，对方先输。

其实这两题的思维方法都来自轴对称图形的基本特征，教师在教学完轴对称图形的内容后可以适当的渗透这方面的知识，学生即乐于学习，又加深对轴对称图形知识的运用和深层理解，发现对称的美，感受到数学的魅力。

如何使用对称关系解决实际问题对称关系是一个很有用的数学概念，可以帮助我们解决实际问题。

在解决问题时，我们常常需要对称关系进行分析和运用。

本文将介绍如何使用对称关系解决实际问题。

一、什么是对称关系对称关系是指两个事物在某种属性或特征上具有相似性或一致性的关系。

这种关系可以在几何、代数和图像等领域中应用。

二、使用对称关系解决几何问题对称关系在几何问题中有着广泛的应用。

常见的对称关系包括：轴对称、中心对称和角度对称等。

1. 轴对称轴对称是指图形具有关于某条直线对称的特点。

在解决与轴对称有关的几何问题时，我们可以通过复制一部分图形到相对的位置来确定对称图形的形状和位置。

例如，我们要绘制一张轴对称图形，可以先在纸上画一半，然后将纸沿着对称轴对折，使两边完全重合，即可得到完整的轴对称图形。

通过对轴对称图形的研究，我们可以得到一些关于对称轴上的性质或特征。

2. 中心对称中心对称是指图形具有关于某一点对称的特点。

在解决与中心对称有关的几何问题时，我们可以通过确定对称中心和对称点之间的关系来确定图形的性质。

例如，我们可以通过绘制对称中心和对称点之间的连线，观察连线的性质，以判断图形是否具有中心对称性。

中心对称图形在我们的生活中有很多实际应用，比如雪花、花朵等。

3. 角度对称角度对称是指图形在某一角度上具有相似性或一致性的特点。

在解决与角度对称有关的几何问题时，我们可以通过确定图形内部角度的性质，来判断它们是否具有角度对称性。

例如，当我们在解决相似三角形问题时，可以通过观察三角形内部的角度关系，找到相似性质，从而得出结论。

角度对称性在涉及旋转、旋转体和立体几何等问题中都有重要应用。

三、使用对称关系解决代数问题对称关系在代数问题中也有广泛应用。

常见的对称关系包括：奇偶性、周期性和函数对称性。

1. 奇偶性奇偶性是指函数在坐标系中某一点的性质。

在解决与奇偶性有关的问题时，我们可以通过判断函数的对称性来确定其奇偶性。

例如，当我们研究关于奇偶函数的性质时，可以通过观察函数的图像是否关于坐标轴对称来判断函数的奇偶性。

生活中的轴对称小论文
轴对称图形在我们的身活中，广泛运用着。

如我们玩的风筝呀，还有那些美丽的蝴蝶……都是轴对称图形。

在我国古代，用到的轴对称图形也有很多，比如说皇宫呀，塔呀，还有家里的花园、亭子呀，等等。

就连现在，一些建筑物也有利用轴对称的原理。

再比如说在美术里不是有“对称美”吗？讲的就是轴对称图形。

轴对称不仅在设计方面有很大的用途，就连在我们算路程时，也能用到轴对称。

比如说，有一次，要在一条河边，给甲、乙村造水电站，问造在河边哪里，离甲、乙村的路程都是最短的？（如图）
首先，我们先表示甲、乙村和河的所在处，画好之后，我们把甲村向河做一条垂线，做完后，我们可把河当一条对称轴，再做一条与上面一样长的垂线得到甲2，再连一条直线到乙，这条直线与河岸的交叉点就是发电站的位置。

如果大家不信，那我们再来验证一下，（如图）。

假设现在水电站在D处，那现在的路程就是从E到D再到A，
也就相当于E到D再到B。

原来的路程应该是从E到C再到B或A都行。

看图，ED+DB大于EC+CB。

EC+CB=EC+CA，ED+DB=ED+DA，那也就说明EC+CA小于ED+DA，这就可以证明水电站设在C处比设在D处路程更短一点，当然是把水电站设在C处好了。

数学，在生活中像这样的例子太多太多了，只要你细心观察，还会有更惊奇的发现。

数学可以美化我们的生活，可以运用到我们的生活中。

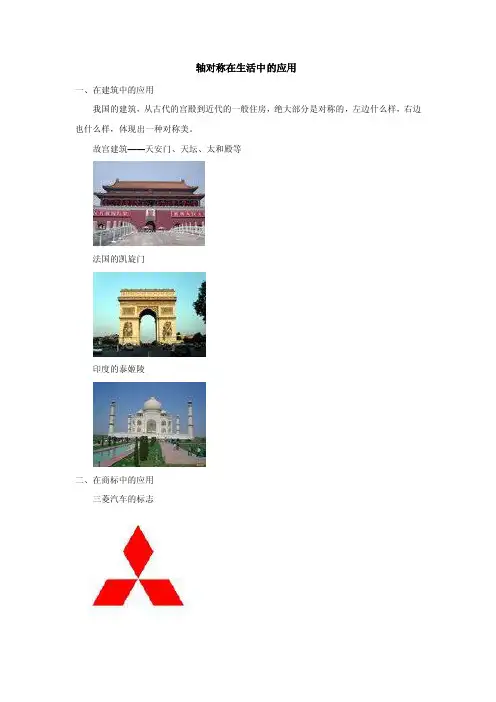
轴对称在生活中的应用
一、在建筑中的应用
我国的建筑，从古代的宫殿到近代的一般住房，绝大部分是对称的，左边什么样，右边也什么样，体现出一种对称美。

故宫建筑——天安门、天坛、太和殿等
法国的凯旋门
印度的泰姬陵
二、在商标中的应用
三菱汽车的标志
中国国徽
三、生活中的应用
生活中的“喜喜”字；闹钟的对称保证了走时的均匀性；飞机的对称使飞机能在空中保持平衡；人的眼睛的对称使人观看物体能够更加准确、全面；双耳的对称能使听到的声音具有较强的立体感。

坐标轴对称的原理和应用1. 坐标轴对称的定义在数学中，坐标轴对称是指一个图形相对于坐标轴进行翻转后与原图形完全重合。

这意味着图形在坐标轴对称的操作下不发生变化，可以说它具有自我重复的性质。

2. 坐标轴对称的原理坐标轴对称的原理主要基于平面几何的基本概念。

在笛卡尔坐标系中，以原点为中心构建两条互相垂直的轴，分别称为x轴和y轴。

对于平面上的点，可以通过坐标表示其位置，其中x轴负半轴为负数，正半轴为正数，y轴同理。

当一个图形在该坐标系中具有坐标轴对称性时，其关于x轴和y轴的坐标具有关系：对于任意一个点 P(x, y)，都有P’(-x, y) 和P’(x, -y) 也在图形中。

通过这种对称性原理，我们可以在图形构建、几何运算和数学推导等方面进行应用。

3. 坐标轴对称的应用3.1 几何图形构建坐标轴对称性在几何图形构建中被广泛应用。

通过利用坐标轴对称性，可以轻松地构建各种对称图形，如正方形、长方形、圆形、菱形等。

以正方形为例，当我们确定了一个顶点的坐标后，可以通过对称性，快速计算出其它三个顶点的坐标。

3.2 几何运算坐标轴对称性在几何运算中有很多实际应用。

例如，在计算图形的面积时，可以利用坐标轴对称性将复杂的图形划分成多个简单的对称部分，再计算每个部分的面积并相加得到最终结果。

同样，计算图形的周长、体积等也可以通过利用坐标轴对称性来简化计算步骤。

3.3 数学推导坐标轴对称性在数学推导中也起到重要作用。

例如，在解方程、证明定理等数学问题中，通过利用坐标轴对称性可以简化问题的形式，从而更容易找到解题的突破口。

特别是在数学分析、线性代数、几何等学科中，坐标轴对称性的应用非常常见。

3.4 物理学应用坐标轴对称性在物理学中也有广泛的应用。

在力学、电磁学、热力学等领域，通过利用坐标轴对称性可以简化物理问题的求解过程。

例如，在力学中，通过利用系统的对称性可以简化运动方程的推导；在电磁学中，坐标轴对称性可以帮助我们找到问题的对称点从而进行简化计算；在热力学中，坐标轴对称性可以帮助我们推导出简化的热传导方程。

中心对称与轴对称的区别及应用对称在我们生活中是一个很常见的概念，可以说是几何学中最基础的概念之一。

在几何学中，对称主要分为两类，一类是中心对称，另一类是轴对称。

那么这两种对称的区别是什么呢？又有哪些应用呢？下面我们来一起探讨一下。

一、中心对称和轴对称的定义我们先来看一下中心对称的定义，“中心对称是指平面中存在一个点，经过这个点作图形内的任意一点与该点的连线，不随着这个内部点的位置而改变的变换。

”简单来说，就是图形被以一个点为中心，对称到对称轴的另一侧，而图形上的所有点到中心的距离相等。

接下来再来看轴对称的定义，“轴对称是指平面中存在一条直线，经过这条直线作图形内的任意点与该直线的连线，距离与垂线长不变的一种变换。

”也就是说轴对称是图形以一个轴线为对称轴，把图形对称到对称轴的另一侧，而对称轴上的点到对称轴的距离为0，其他点到对称轴的距离相等。

二、中心对称和轴对称的区别从定义上我们可以看出，中心对称和轴对称两者的主要区别在于基本元素不同，中心对称以点为基本元素，轴对称以直线为基本元素。

这也造成了二者性质和应用上的差异。

（1）性质的差异在性质上，我们可以看出，中心对称的对称轴是一条点，图形与其对称轴对应的位置称为中心对称位。

而轴对称的对称轴是一条直线，图形与其对称轴对应的位置称为轴对称位。

中心对称的变换具有对称性、可逆性和等距性。

但轴对称具有的三种性质都是对称性，但不具有可逆性和等距性。

（2）应用的差异在应用上，中心对称主要用于计算图形中心、判断图形重合和寻找图形的对应点。

而轴对称则广泛应用于建筑设计、机械加工、生物医学等领域。

例如，制作对称的模具、设计对称的装饰、轴射成像等。

三、结语中心对称和轴对称是几何学中最基本的概念之一，理解它们的区别和应用非常重要。

在实际应用中，根据需要选择相应的对称方式，可以更加方便和高效地进行工作。

我们希望通过这篇文章，更好的理解中心对称和轴对称，并为读者提供更多参考。

生活中的轴对称
生活中的轴对称：生活上有书本，飞机，蝴蝶，排球，足球，篮球，羽毛球拍，灯，柜子，风扇，凳子，桌子，床，被子，沙发，对联，笔盒。

轴对称图形平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形。

生活作用
1、为了美观。

比如天安门，对称就显的美观漂亮。

2、保持平衡。

比如飞机的两翼。

3、特殊工作的需要。

比如五角星，剪纸。

扩展资料：
实际区别时轴对称图形要像折纸一样折叠能重合的是轴对称图形；中心对称图形只需把图形倒置，观察有无变化，没变的是中心对称图形。

现将小学课本中常见的图形归类如下：既是轴对称图形又是中心对称图形的有：长方形，正方形，圆，菱形等。

只是轴对称图形的有：角，五角星，等腰三角形，等边三角形，等腰梯形等等。

只是中心对称图形的有：平行四边形。

既不是轴对称图形又不是中心对称图形有：不等边三角形，非等腰梯形等。

一个图形既轴对称又中心对称一定有两条或两条以上的对称轴。

生活中的轴对称美国数学家克莱因曾对数学美作过如此的描述：音乐能激发或抚慰情怀，绘画使人赏心悦目，诗歌能动人心弦，哲学使人获得聪慧，科技能够改善物质生活，但数学却能提供以上一切。

下面就让我们一起来看看数学是如何样让人赏心悦目的。

轴对称图形是沿着某直线折叠后，直线两旁的部分互相重合的图形。

这条直线确实是他们的对称轴。

这条对称轴就像一个公平的法官，左右两边的长度、面积、形状等，都一点儿也不差，唯独不同的确实是他们所朝的方向。

在数学课本里，我们已见过它们的身影，也接触、了解过它们。

下面让我们一起看看生活当中的轴对称图形。

当我们闲逛在校园时，随手捡起一片树叶，假如将树叶中间的那根茎当成是其左右两边的对称轴，将树叶右边部分沿着这条对称轴对折过去，我们会惊奇地发觉它正好与左边的一半树叶重合。

一只蝴蝶停留在花朵上，张合着翅膀时，假如将蝴蝶两只触角的中点与尾部相连接，连接好的线段所在的直线确实是其对称轴。

而右边的翅膀就像是左边的翅膀沿着对称轴翻折过去的图形。

像蝴蝶如此成轴对称图形的动物还有专门多，比如蜻蜓、飞蛾、螃蟹等。

动物进化经历了由海绵动物、双胚层辐射对称动物（包括腔肠动物）、三胚层两侧对称动物的进展时期，其中从辐射对称动物到两侧对称动物的演化，是生物进化过程中的一个重大事件，它意味着一系列遗传基因的重要创新，并由此促进生命的形状、行为向更加复杂的时期快速进展。

“贵州小春虫”的发觉，将生物进化史上的一个重要时期——两侧对称动物化石记录的历史前推到了寒武纪之前4000万年。

对称是动物的美学，左右对称是动物世界普遍的健康、强壮的特点。

人类的耳、眼、四肢差不多上对称生长的。

耳的轴对称不仅使我们听到的声音具有强烈的立体感，还能够判定声源的位置；眼的对称使我们看物体更清晰、准确。

演出前化妆时，你确信不期望眉毛被画得一高一低、两边眼线不一样粗细吧？这就要求化妆师随时把轴对称放在内心。

中国银行的图形标志也是一个轴对称图形。

生活中常见的轴对称图形
镜面反射，生活中的轴对称图形。

在我们的日常生活中，轴对称图形无处不在。

无论是自然界中的植物和动物，
还是人造物品中的建筑和艺术品，都可以找到轴对称图形的身影。

轴对称图形是指图形中存在一个轴，使得图形关于这个轴对称。

这种对称美不仅存在于数学中，更在生活中展现出无限的魅力。

首先，让我们来看看自然界中的轴对称图形。

许多植物的叶子和花瓣都具有轴
对称的特点，比如玫瑰花瓣的排列和荷叶的形状。

这种对称美让人感到舒适和和谐，也给人们带来了无尽的灵感。

动物身上也有许多轴对称的特征，比如蝴蝶的翅膀和海星的身体。

这些轴对称图形不仅美丽动人，更是大自然的杰作。

其次，人造物品中也充满了轴对称图形的魅力。

建筑中的许多设计都采用了轴
对称的原则，比如古希腊的庙宇和现代的摩天大楼。

这种对称美不仅让建筑更加稳固和美观，也让人们感受到了宁静和谐。

艺术品中也有许多轴对称图形的表现，比如中国的对联和西方的雕塑。

这些作品不仅展现了艺术家的才华，更让人们感受到了美的力量。

总的来说，轴对称图形在我们的生活中无处不在，它们展现了自然界和人类创
造的美丽和和谐。

无论是自然界中的植物和动物，还是人造物品中的建筑和艺术品，轴对称图形都给人们带来了无尽的惊喜和感动。

让我们珍惜这些美丽的轴对称图形，让它们成为我们生活中的一部分，让我们的生活因此更加丰富多彩。

三年级数学教学案例：轴对称图形在活中的应用一、课题概述这次数学课的主题是轴对称图形在生活中的应用。

轴对称是数学中一个重要的概念，它在美术、建筑、电子游戏等方面都有广泛的应用。

在这节课中，我们将学习轴对称的基本概念和判定方法，并通过一些生活中常见的例子来深入理解和应用轴对称。

、教学目标1.了解轴对称的定义和性质，掌握判定轴对称的方法；2.能够在生活中识别轴对称图形，体会轴对称图形的美；3.能够应用轴对称在美术、建筑、电子游戏等方面，提高综合素质。

三、教材分析1.“轴对称”的定义和性质轴对称是指平面内用一条直线将一个图形分成两个对称的部分，这条线称为轴线或对称轴。

轴对称有三个基本性质：（1）轴线上的任意点到对称点的距离相等；（2）对于轴线一侧的任意一点，如果将它到轴线的距离作为半径画一个圆，那么它的对称点也应该在此圆上；（3）轴对称不改变图形的大小和形状。

2.判定轴对称的方法判定一个图形是否具有轴对称可以采用以下两种方法：（1）将图形折叠在对称线上，如果两半完全重合，则具有轴对称；（2）如果将图形旋转180度后恰好与原来的图形重合，则也具有轴对称。

四、教学过程1.“轴对称”的概念与性质（1）引入轴对称的概念，通过举一些例子和动手实践来帮助学生理解轴对称的基本概念和性质；（2）通过对比对称图形和非对称图形的特点，引导学生发现轴对称的特点和应用；（3）通过生动的例子和手工制作轴对称图形，来帮助学生深入理解和掌握轴对称的原理和应用。

2.轴对称在生活中的应用（1）掌握一些轴对称的实际例子，如花朵、蝴蝶、翅膀、雪花等，通过欣赏和观察这些图形，来加强学生对轴对称的认识和应用；（2）应用轴对称在美术创作中，引导学生制作一些轴对称的图案和图形进行展示和交流；（3）引导学生思考轴对称在建筑和电子游戏等方面的应用，并让学生自由发挥，进行小组讨论和展示。

五、教学评价通过这节数学课的教学，学生将充分认识到轴对称的概念和性质，并能够应用轴对称在实际生活中。