博弈论第2讲详解
- 格式:pdf
- 大小:903.86 KB
- 文档页数:138








第二讲博弈论在公共管理中的应用第二讲博弈论在公共管理中的应用一1>.公共管理要了解博弈论1.几个富有启发性的案例(1)商家作出最低价格承诺的真相是什么?所谓最低价格承诺是指商家承诺自己的价格比任何对手都低,一旦有对手的价格比自己低,作承诺的商家将退回差额,并且承诺支付一定金额的违约罚金。
思考:商家为什么要作出这种承诺呢?是为了促销或者恶性竞争吗?(2)假设有三个候选人或候选方案:x、 y 和z;有三个参加投票的人:甲、乙、丙。
三个人对候选对象的态度分别如下:甲:x y z;乙:y z x;丙:z x y。
(注:候选对象排位越靠前,表示越喜欢)现在分别有三个投票程序:程序1,x与y先pk,然后胜利者进入下一轮与z进行pk;程序2,x与z先pk,然后胜利者进入下一轮与y进行pk;程序3,z与y先pk,然后胜利者进入下一轮与x进行pk。
思考:(1)上面每个程序的最终获胜者是谁?(2)为了保证丙自己心目中最喜欢的z当选,如果丙能够操纵投票程序,他应该采用哪个投票程序?(3)如果您是甲,为了避免自己最不喜欢的丙当选,应该怎么办?(3)开店博弈假设顾客均匀分布在一条街上,他们总是选择到离自己家最近的商店购物;现有两位投资者均准备在街上开店,他们都希望到自己商店购物的顾客越多越好。
请问:投资者应该把商店开在哪里?A.开店博弈的启示:a,开店要扎堆,而且要扎在中心地带;b,商业中心是商家博弈自发的结果,政府打造商业中心应该顺应这一规律。
B.开店博弈在政治领域的启示:a,你的竞选纲领应该持中间派立场;b,你的竞选纲领应该模棱两可,使得左右两派都能从中找到对自己有利的解释。
2.什么是博弈?(1)参与博弈的各方在利益上存在或多或少的冲突、差异,这是形成博弈的基本要素。
(2)参与博弈的各方所获得的最终结果既取决于自己的决策,也取决于对手的决策。
(3)参与博弈的任何一方在决策时必须考虑对手的反应并根据对手的反应来制定自己的最佳策略(思考:为什么田忌赛马不是博弈?因为齐王根本没有博弈的意识)。
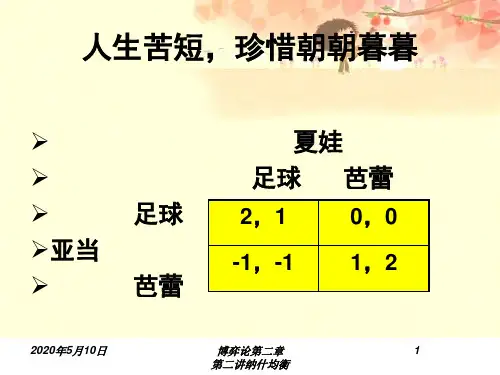
第二讲完全信息静态博弈主要内容⏹基本分析思路和方法⏹纳什均衡⏹混合策略和混合策略纳什均衡⏹纳什均衡的存在性⏹纳什均衡的选择和分析方法扩展例: 房地产开发项目-假设有A、B两家开发商市场需求:可能大,也可能小投入:1亿A、B同时决策假定市场上有两栋楼出售:✓需求大时,每栋售价1.4亿,✓需求小时,售价7千万;如果市场上只有一栋楼✓需求大时,可卖1.8亿✓需求小时,可卖1.1亿完全信息静态博弈⏹完全信息☐每一个参与人对所有其他参与人的特征(策略空间,支付函数)有完全的了解⏹静态☐指所有参与人同时选择行动且只选择一次。
☐同时选择⏹只要每一个参与人在选择自己的行动的时候不知道其他参与人的选择,我们就称之为“同时选择”⏹博弈分析的目的:预测博弈的均衡结果☐给定每一个参与人都是理性的☐每一个参与人都知道其他人是理性的☐找出每一个参与人的最优策略☐所有参与人的最优策略博弈的策略式表述(标准式表述)⏹每一个参与者的组合同时选择一个策略,所有参与者选择的策略的组合决定了每一个参与者的收益。
⏹博弈参与人:☐决策主体,通过现在行为(策略)以最大化自己的效用☐“自然”:虚拟的参与人,决定外生随机变量的概率分布的机制,没有自己的目标函数和支付函数.如,天气.⏹每一个博弈参与人的策略空间⏹如果博弈参与人每人选择一个策略,n 维向量称为策略组合,其中是的i 个参与人的选择策略.{}1,2....,N n =,1,2i S i n = 1(,)n S S S = i S博弈的策略式表述⏹支付以及支付函数☐支付:指在一个特定的策略组合下参与人得到的确定效用水平,或者是指每一个参与人得到的期望效用水平.☐支付函数(效用函数):⏹博弈:1(,)i n u S S },;,{11n n u u S S G博弈的策略式表述(例)⏹囚徒困境☐博弈者:囚徒1,囚徒2☐每一个博弈者的策略空间:☐支付函数:-10,-100,-20-20,0-1,-1坦白不坦白坦白不坦白两个罪犯的得益矩阵囚徒2囚徒11(,)20π=-不坦白坦白{}12,S S ==坦白不坦白博弈的策略式表述(例)双寡头古诺竞争{}121121121121221222N 1,2:=(0,):(,)()()(,)()()S S S S S P S S c S S S S P S S c S ππ==∞=+-=+-博弈者:两家厂商每一个博弈者的策略空间支付函数基本分析思路和方法⏹策略式博弈原则☐如果一个参与者有占优策略的话,他应该使用这个策略。
当所有参与者都具有占优策略而且都使用它们,其结果就是占优策略均衡(所有参与人的最优策略的组合)。
⏹完全信息策略式博弈原则☐一个博弈的参与者永远不应该使用劣策略。
对于某些适当的博弈,可以用重复剔除劣策略求解⏹策略式博弈原则☐任何博弈中的所有参与者最终将选择一个纳什均衡。
占优均衡⏹占优策略:不管其它博弈方选择什么策略,一博弈方的某个策略给他带来的得益始终高于其它的策略,至少不低于其他策略的策略。
即,无论其他参与者如何选择,他的最优策略是唯一的囚徒的困境中的“坦白”;双寡头削价中“低价”。
(不依赖于对方的选择)一般地,称为参与人i 的(严格)占优策略,如果对应的所有的是i 的严格最优选择,即:对应的,所有被称为“劣策略”。
是除i 之外的所有参与人策略的组合。
⏹占优策略均衡:如果在某一个博弈中,每一个博弈者都有一个占优策略,那么就是这个博弈的占优策略均衡(强占优)*i s *,i i s s -*''*(,)(,),i i i i i i i i i u s s u s s s s s--->∀∀≠'*i i s s ≠111(,...,,...)i i i n s s s s s --+=*i s ***12(,,...)n s s s例1 二价拍卖策略式博弈的描述{}12N 1,2,....,,:=....[0,)max max :(,P )0max i j i j i j i j i i i i j i j N S S V P P P u P P P ≠≠-≠===∞->⎧⎪=⎨<⎪⎩博弈者:代表所有的竞争者每一个博弈者的策略空间支付函数例:一群赌徒在赌钱,每个人将钱放在自己身边(每个人都知道自己的钱有多少),忽然吹来一阵风将所有的钱都混在一起,使他们无法分辨哪些钱是自己的,纳什均衡为他们解决这个问题。
⏹他们请来律师,律师宣布规则:☐每个人都将钱数写在纸条上,然后交给律师。
☐如果所有人要求的钱数加总不大于钱的总数,每一个人都得到自己要求的部分(如果有剩余的话,剩余部分归律师所有)。
☐如果所有人要求的钱数加总大于钱的总数,所有钱都归律师所有。
这个问题的Nash均衡是每个都拿自己的钱数。
其他任何一种分配方案中,都会有人多拿钱,有人少拿钱,少拿钱的人会后悔。
分析:我们现在假设只有2 个参与者A、B ,二者原本手中货币均为50(相互之间不知道其他人有多少钱,钱混在一起后也不知道总共有多少钱),现在,由于金钱混到一起,于是A和B 都想混水摸鱼,多得一部分钱,再假设都想得到60,那么写出支付矩阵:分析: 收益矩阵分析:⏹通过上面的支付矩阵,我们可以得出答案,只有A 和B都做出选择得到50 的时候,他们才能得到钱,不多一分也不少分,如果有一方想多得,二者将一分也得不到,钱全部归律师所有。
⏹拓展到N 人博弈,理性博弈者可以从最简单的二人博弈中发现每个人的最优策略仍然是只拿到自己本有的金额,否则,一人的多得将会导致所有人都没有,而这是一个最差的结果,按照不多得的策略,至少还可以得到自己应有的那一份。
占优均衡0.5 ,2.5-0.5,42,1.50, 0踩不踩踩不踩大猪小猪⏹占优均衡:一个博弈的某个策略组合中的所有策略都是各个博弈方各自的占优策略,必然是该博弈比较稳定的结果。
⏹占优均衡是一个非常合理的预测。
⏹占优均衡不是普遍存在的,如,智猪博弈⏹踩一次出现4份食物⏹踩一次各猪消耗0.5单位的能量,但是,都踩,大猪得3份,小猪得1份大猪的最优选择要依赖于小猪重复剔除劣策略方法劣策略:不管其它博弈方的策略如何变化,给一个博弈方带来的收益总是比另一种策略给他带来的收益少的策略。
'''''''''''''''''''''i ,,i (,)(,)iiii i i iii ii i ii iiiiiii s s s s S s s s u s s u s s s s s s s s s ----∈∈<∀i 定义:令和是参与人可选择的两个策略,即S 。
如果对于任意的其他参与人的策略组合参与人从得到的支付严格小于从选择得到的支付,即:我们说策略严格劣于。
通常,称为相对于的劣策略,称为相对于的占优策略。
重复剔除劣策略方法重复剔除的占优策略均衡:策略组合称为重复剔除的占优策略均衡,如果它是重复剔除劣策略后剩下的唯一策略组合。
如果这种唯一的策略组合存在的,我们就说该博弈是重复剔除占优可解的。
***1(,...)n s s s重复剔除劣策略方法的步骤:1.找出某个参与人的劣策略(假定存在),将这个劣策略剔除,重新构造一个不包含已剔除策略的新的博弈2.然后在继续剔除新的博弈中的某个参与人的劣策略,继续这个过程,一直到仅仅剩下一个唯一的策略组合为止.重复剔除劣策略方法⏹踩一次出现4份食物⏹踩一次各猪消耗0.5单位的能量,但是,都踩,大猪得3份,小猪得1份0.5 ,2.5-0.5,42,1.50, 0踩不踩踩不踩大猪小猪重复剔除劣策略方法⏹缺点☐参与人是理性的☐要求“理性”是共同知识☐博弈结果对双方行为的不确定性很敏感⏹需要一种适用性较强的博弈分析方法,该方法是以策略之间的相对优劣关系为基本。
8,10-10000,97,66,5U RLD试用重复剔除劣策略方法求解双寡头古诺模型的纳什均衡1212()10Q s s P P Q Scc=+==-==例2双寡头古诺模型用重复剔除劣策略的方法寻找均衡需要满足的条件:⏹利润函数是严格凹的(二阶导数小于0)⏹交叉偏导数为负的(反应函数是斜率为负的连续函数,且只交叉一次,交叉点上R1比R2更陡)稳定的均衡是存在的,且是唯一的纳什均衡的定义⏹策略空间:⏹博弈方的第个策略:⏹博弈方的得益:⏹博弈:纳什均衡:在博弈中,如果由各个博弈方的各一个策略组成的某个策略组合中,任一博弈方的策略,都是对其余博弈方策略组合的最优策略,也即对任意都成立,则称为的一个纳什均衡n S S ,1ij i S s ∈i u },;,{11n n u u S SG =},;,{11n n u u S S G =),(**1n s s i ),...,,(**1*1*1n i i s s s s +- ********1111(,,,,...)(,,,,...)i i i i i n i i i ij i n u s s s s s u s s s s s -+-+≥ i j i S s ∈),(**n i s s G i i j *i s纳什均衡的含义⏹当其他人策略固定时,每一个人采用的策略是最好的⏹信念问题:每一个人都相信其他人都采用最优策略⏹如果不是Nash均衡,一定至少有一个人有动机偏离均衡,即均衡是不稳定的。
纳什均衡与重复剔除劣策略法占优均衡肯定是纳什均衡,但纳什均衡不一定是占优均衡命题2.1:在n 个博弈方的博弈中,如果重复剔除劣策略法排除了除之外的所有策略组合,那么一定是该博弈的唯一的纳什均衡命题2.2:在n 个博弈方的博弈中中,如果是的一个纳什均衡,那么重复剔除劣策略法一定不会将它消去上述两个命题保证在进行纳什均衡分析之前先通过重复剔除劣策略法简化博弈是可行的),(**n i s s },;,{11n n u u S S G =),(**n i s s ),(**n i s s },;,{11n n u u S S G =G纳什均衡的一致预测性质⏹一个策略构成纳什均衡策略的唯一条件是参与人对于其他参与人均衡策略的最优选择。
⏹一致预测:如果所有博弈方都预测一个特定博弈结果会出现,所有博弈方都不会利用该预测或者这种预测能力,选择与预测结果不一致的策略,即没有哪个博弈方有偏离这个预测结果的愿望,因此预测结果会成为博弈的最终结果。
☐只有纳什均衡才具有一致预测的性质☐一致预测性是纳什均衡的本质属性,所谓“一致”是指各博弈方的实际行为选择与他们的预测一致,而不是不同博弈方的预测相同,无差异。
☐一致预测并不意味着一定能准确预测,因为有多重均衡,预测不一致的可能划线法在每一个博弈方对其他博弈方每一个策略或者策略组合(对多人博弈)的最佳策略对应的收益下划线。