博弈论第二章
- 格式:doc
- 大小:296.50 KB
- 文档页数:26







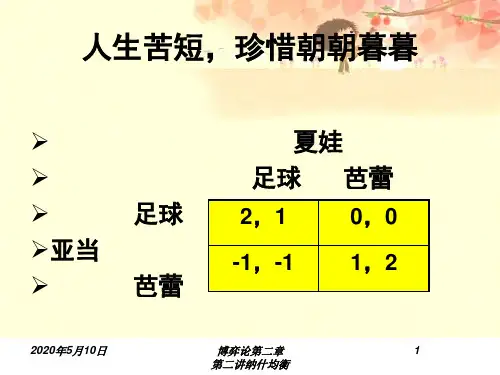



问题1:博弈方2就如何分10000元钱进行讨价还价。
假设确定了以下原则:双方提出自己要求的数额1s 和2s ,10000021≤≤s s ,。
如果设博弈方1和,1000021≤+s s ,则两博弈方的要求都得到满足,即分得1s 和2s ;但如果1000021>+s s ,则该笔钱就被没收。
问该博弈的纯策略纳什均衡是什么?如果你是其中一个博弈方,你会选择什么数额,为什么?解:112111210000()010000s s s u s s s ≤-⎧=⎨>-⎩,那么,1210000s s =-221222110000()010000s ss u s s s ≤-⎧=⎨>-⎩那么,2110000s s =-它们是同一条直线,1210000s s +=上的任意点12(,)s s ,都是本博弈的纯策略的Nash 均衡。
假如我是其中一个博弈方,我将选择15000s =元,因为(5000,5000)是比较公平和容易接受的。
它又是一个聚点均衡。
问题2:设古诺模型中有n 家厂商。
i q 为厂商i 的产量,n q q q Q +++= 21为市场总产量。
P 为市场出清价格,且已知Q a Q P P -==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为ii i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?解:1()ni i i j i j pq cq a c q q π==-=--∑,1,2,,i n =令20ii j j ii a c q q q π≠∂=---=∂∑,1,2,,i n =解得:***121na c q q q n -====+,2***121na c n πππ-⎛⎫==== ⎪+⎝⎭当n 趋向于无穷大时,这是一个完全竞争市场,上述博弈分析方法其实已经失效。
2 完全信息的动态博弈2.1完全和完美信息的动态博弈动态博弈(dynamic game):参与人在不同的时间选择行动。
完美信息(perfect information): 在博弈的每次行动的参与人完全知道博弈的历史。
2.1.A 理论: 逆向归纳法简单的完全和完美信息博弈:1. 参与人 1 选择行动a 12. 参与人 2 观察a 1,然后选择a 23. 收益是 u 1(a 1, a 2)和u 2(a 1, a 2)求解博弈: 逆向归纳法 (backward induction)1. 求解第二个阶段,对于a 1,求a 222max A a ∈u 2(a 1,a 2)其解: a 2= R 2(a 1) ---- 反应函数2. 求解第一个阶段11m a x A a ∈ u 1(a 1,R 2(a 1))其解: a *1逆向归纳解(outcome): (a *1, R 2(a *1) )注意:在动态博弈中,行动与战略是不同的概念;逆向归纳解与纳什均衡是不同的概念。
关于逆向归纳法的理性假定例11L R220 L'R'111 L''R''3 00 2用逆向归纳法:第3步:参与人1 选择L'';第2步:参与人2 选择L';第1步:参与人1 选择L逆向归纳解: L(在第一个阶段结束)。
如果博弈在第一个阶段中不结束,可能原因是什么?2.1.B Stackelberg 模型二个企业,生产产量: q1, q2市场需求: P = a–Q, 其中Q = q1 + q2成本: C i (q i) = cq i, i = 1, 2.利润:πi (q1, q2) = Pq i–C i (q i) = (a– (q1 + q2))q i–cq i,博弈的顺序:(1) 企业1 选择q1≥ 0;(2) 企业2 观察q1然后选择q2≥ 0;(3) 收益: πi (q i , q j ) = q i [P (Q ) – c ]其中P (Q) = a – Q , Q = q 1 + q 2求逆向归纳解(1)阶段2,企业2在观察q 1后选择q 2满足02max ≥q q 2 (a – (q 1 + q 2) – c )解出q 2 = R 2 (q 1) =21cq a --(2)阶段1,企业 1知道R 2 (q 1),求q 101max ≥q q 1 (a – (q 1 + R 2 (q 1))– c )=01max ≥q q 1 21c q a --解出q 1* =2ca -, R 2(q 1*) =4ca -与 Cournot 模型比较q 1* = q 2* =3ca -结果:先进入市场者有更多的利润。
2.1.C 工会与企业的工资和就业一个企业和一个工会,关于工资w 和就业数量L 的决定。
工会收益: U (w , L );企业收益: π(w , L ) = R (L ) – wL ,R '(0) = ∞ ,R '(∞) = 0 博弈的顺序:(1) 工会选择工资w ;(2) 企业观察 w 且选择 L .wL工会的无差异曲线求逆向归纳解(1) 阶段2企业对w,选择L求max [R(L) –wL]一阶条件R'(L)–w = 0RR(L)L(w) L可以得到企业的反应函数:L(w)利用等利润曲线π = R(L) –wL分析:1. w = (R(L) –π)/L,等利润线的位置越低,利润越大;2. dw/dL = [R'(L) –w]/L,随L增加,等利润曲线先是正斜率,然后是负斜率。
3. 企业的选择在等利润线的顶点上。
w L (w)L(2) 阶段1工会知道L(w),求Max U(w, L)s. t. L = L(w)逆向归纳解(w*, L(w*))w L (w)L此结果是非最优的(inefficient)。
2.1.D 序贯谈判参与人1 和参与人2 谈判分配一元钱(s, 1 –s ).三期的谈判模型(1a) 参与人1 提议分配方案:(s1, 1 –s1 );(1b) 参与人2接受提议或拒绝提议。
如果参与人2拒绝,进入第2阶段;(2a) 参与人2提议 (s 2, 1 – s 2 )(2b) 参与人 1接受提议或拒绝提议。
如果参与人1拒绝,进入第3阶段;(3) 按外生方案分配,参与人 1 分得s ,参与人2分得1–s 。
贴现率: δ求逆向归纳解(1) 在阶段 2如果s 2 ≥ δs 参与人 1 将会接受s 2。
取s 2 = δs ,则1 – s 2 ≥ δ(1 – s )。
结果: 参与人 2 将会提议 s *2 = δs ,参与人 1 将会接受。
(2) 在阶段 1如果 1 – s 1 ≥ δ(1 – s *2) 即 s 1 ≤ 1 – δ(1 – s *2 ) ,参与人 2 将会接受 s 1当 s 1 = 1 – δ(1 – s *2 ), s 1 ≥ δs *2结果: 参与人 1 将会提出s *1 = 1 – δ(1 – s *2 ) = 1 – δ(1 –δs )参与人 2 将会接受 1 – s *1.逆向递归解为[1 – δ(1 –δs ), δs ]无限时间情形:不存在外生终止时间,无限重复阶段1与2。
假设结果是在第1期分配 (s 1*, 1 – s 1*)。
而在第1期和第2期未结束,在第3期分配 (s , 1 – s )。
第一期结果与第三期相同。
s = s *1 = 1 – δ(1 – s *2 ) = 1 – δ(1 –δs )结果s =δ+11, 1 – s = δδ+12.2 完全非完美信息二阶段博弈2.2.A 理论: 子博弈精炼完全非完美信息的二阶段博弈:(1) 参与人1 和2 同时选择a1和a2;(2) 参与人3 和4 观察(a1, a2), 然后同时选择a3 和a4;(3) 收益是u i(a1, a2, a3, a4), i =1, 2, 3, 4.逆向归纳法在第二阶段博弈, 参与人3 和4: (a*3(a1, a2), a*4(a1, a2)).在第一阶段,参与人1 和参与人2: (a*1, a*2).子博弈精炼解(sub-game perfect outcome)(a*1, a*2, a*3(a*1,a*2), a*4(a*1, a*2))2.2.B 银行挤提二个投资者在一个银行存款D.银行: 如果提前变现,得:2r如果到期,得:2R在期1投资者2提款不提提款r,r D,2r–D投资者1不提2r– D, D下阶段在日期2提款不提提款R,R2R–D,D不提D, 2R–D R, R求子博弈精炼解(1) 在期2, (取款,取款), 收益(R, R)(2) 将第2期收益代回,在期1,提款不提提款r,r D,2r– D不提2r–D, D R, R二个纯战略纳什均衡: (取款,取款),(不取,不取).两阶段博弈有二个子博弈精炼解:在日期1 两人都取款, (r, r);在日期1 两人都不取款, 但是在日期2 取款, (R, R)。
2.2.C 关税和国际市场竞争两个国家:1,2。
每国市场需求:P i(Q i) = a–Q i = a– (h i+ e j ),政府:制定关税t i企业:生产产品供给本国h i和出口e i生产成本C = c(h i+ e j)博弈的时间顺序政府选择关税企业观察税率,选择产量企业收益为利润πi (t i , t j , h i , e i , h j , e j ) =[a –(h i + e j )]h i +[a –( e i + h j )] e i – c (h i + e i )– t j e i 政府收益为本国总福利w i (t i , t j , h i , e i , h j , e j ) =21Q i 2 + π(t i , t j , h i , e i , h j , e j ) + t i e j求子博弈精炼解第2阶段,两个企业的纳什均衡在观察t i 与t j 后,国家i 的企业选择(h i , e i ),求max πi (t i , t j , h i , e i , h j , e j )有一阶条件d πi /dh i = a – 2h i –e j – c = 0d πi /de i = a – 2e i – h j – (c + t j ) = 0两个企业的反应函数h 1* =21(a – e 2* – c ) e 1* =21(a – h 2 * – c – t 2) h 2* =21(a – e 1* – c ) e 2* =21(a – h 1* – c – t 1) 可以解出h 1* =31(a – c + t 1 ) e 1* =31(a – c – 2t 2) h 2* =31(a – c + t 2 ) e 2* =21(a – c – 2t 1)第1阶段,两个政府的纳什均衡w i (t i , t j , h i , e i , h j , e j ) = 21Q i 2 + π(t i , t j , h i , e i , h j , e j ) + t i e j=21Q i 2 +[a – (h i + e j )]h i + [a –( e i + h j )] e i – c (h i + e i ) – t j e i + t i e j = 21[31(a – c + t i ) + 21(a – c – 2t i )]2 + [a – (31(a – c + t i ) + 31(a – c – 2t i ))]×31(a – c + t i ) + [a – (31(a – c – 2t j ) + 31(a – c + t j ))]×31(a – c – 2t j ) – c (31(a – c + t i ) +31(a – c – 2t j ))– t j 31(a – c – 2t j ) + t i 31(a – c – 2t i ) 一阶条件dw i /dt i = [31(a – c + t i ) + 21(a – c – 2t i )]( –32) + [a – (31(a – c + t i ) + 31(a – c – 2t i ))]31+31⨯31(a – c + t i ) – c 31+ 31(a – c – 2t i ) - 32t i = 0可解出t i =3c a - 从而h i =9)(4c a - , e i = 9c a -2.2.D 竞赛二个工人和他们的老板.阶段 1, 老板提出工人的工资,: w H , w L (即a 1) 产量高者得高工资,低者得低工资。