当前位置：文档之家 › 三角形全等的判定(aas asa)

三角形全等的判定(aas asa)

  • 格式：doc
  • 大小：58.04 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

全等三角形判定方法3及推论ASA与AAS

全等三角形判定方法3及推论ASA与AAS

∠A=∠D （已知 ）
AB=DE（已知 ）
∠B=∠E（已知 ）
B
∴ △ABC≌△DEF （ASA）
A
D
CF E
例1： 已知如图， O是AB 的中点，∠A=∠B，
求证：△ AOC≌△BOD
证明：
∵ O是AB 的中点(已知） C
∴ OA=OB( 中点定义）
在△AOC和△BOD中 A
1O
B
2
∠A= ∠B (已知）
（ASA）
两角和其中一角的对边对应相等的两个三角形 全等，简写成“角角边”或“ AAS”
（AAS）
两个三角 是否全等（全等画 形中相等 “√”，不全等画 的边或角 “×”
公理或推 论（简写）
三条边
√
两边夹角 √
两边一角 两边与一 边对角
×
两角夹边 √
两角一边 两角与一 角对边
√
三个 角
×
SSS SAS
∴△ABC ≌△DEF（ASA ）
两你角能及从一上角题的中对得到边什对么应结相论等？的 两个三角形全等（ AAS）。
三角形全等判定方法4
有两角和其中一角的对边对应相等的两个三角形全等
(可以简写成“角角边”或“AAS”）。
C
C′
A
B
A′
B′
证明:在△ABC 与△A′B ′C ′中
∠A=∠A ′ ∠B=∠B ′
两角及其中一角的对边。
先任意画一个 △ABC ，再画一个△A′B′C ′ ， 使A′B′=AB , ∠A =′ ∠A， ∠B =′ ∠B
画法: 1.画 A′B ′=AB ； 2.在A′B′ 的同旁画 ∠DA B′ =′ ∠A , ∠EB A′= ′∠B,

三角形全等的判定ASA-AAS及尺规作图五种基本作

三角形全等的判定ASA-AAS及尺规作图五种基本作

以上内容是基于给定的大纲和指令进行的扩 展，但请注意，由于缺乏具体细节和背景信 息，某些描述可能不够精确或全面。如有需 要，请进一步补充和修正。
04
asa-aas在实际问题中的 应用
在几何证明题中的应用
在几何证明题中，asa-aas判定定理常常用于证明两个三角形全等。通过比较两 个三角形的两边和夹角，如果满足条件，则两个三角形全等，从而可以得出其他 相关结论。
asa-aas的发展方向
拓展适用范围
实际应用研究
研究如何将ASA-AAS判定应用于更广 泛的情况，例如处理只有一边和两个 角的情况或者只有两边和夹角的情况。
研究如何将ASA-AAS判定应用于解决 实际问题，例如几何证明、建筑设计、 工程测量等领域。
引入其他判定方法
研究如何将其他三角形全等判定方法 （如SAS、SSS、HL等）与ASA-AAS 判定相结合，以拓展其应用范围。
经过一点做已知直线的垂线
总结词
垂线的作法
详细描述
在给定的直线上选择一个点，然后使 用圆规在该点上画圆，与直线相交于 两点。连接这两点即可得到经过该点 的垂线。
作已知角的角平分线
总结词
角平分线的作法
详细描述
在给定的角内，使用圆规以角的顶点为圆心画圆，与角的两 边相交于两点。连接这两点即可得到该角的角平分线。
Hale Waihona Puke VS应用在尺规作图中，可以利用asa-aas判定三 角形全等来确定未知点的位置。例如，已 知一个三角形的两个角和一边，可以通过 asa-aas判定另一个三角形与之全等，从 而确定未知点的位置。
利用asa-aas解决实际问题
• 实例：在建筑设计中，常常需要确定某一点的位置使得该点到 两个已知点的角度相等。通过asa-aas判定定理，可以确定未知 点的位置，从而满足建筑设计的需求。

12.2三角形全等的判定(ASA,AAS)教案-人教版八年级数学上册

12.2三角形全等的判定(ASA,AAS)教案-人教版八年级数学上册
- AAS（角-角-边）：两个角和其中一个角的对边对应相等的两个三角形全等。
2.学会运用ASA和AAS判定方法判断两个三角形是否全等。
3.通过实际例题，加深对ASA和AAS判定方法的理解，并培养运用这些方法解决问题的能力。
4.能够运用ASA和AAS判定方法解决实际问题，如测量角度和边长，确定物体的形状等。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了三角形全等的ASA和AAS判定方法的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对这些判定方法的理解。我希望大家能够掌握这些知识点，并在解决几何问题时灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
3.重点难点解析：在讲授过程中，我会特别强调ASA和AAS判定的条件和步骤这两个重点。对于难点部分，我会通过具体的图形示例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与三角形全等判定相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。这个操作将演示ASA和AAS判定方法的基本原理。
二、核心素养目标
本节课的核心素养目标主要包括：
1.培养学生的逻辑推理能力：通过探究ASA和AAS判定方法，让学生理解几何图形全等的：通过实际操作和例题分析，使学生能够在空间中正确构建和识别全等三角形，培养他们的空间想象力和直觉思维能力。
-难点三：将理论知识应用于解决具体问题，如实际测量和几何证明。
-解释：学生需要学会如何将ASA和AAS判定方法应用于解决具体问题，例如在给定一些角度和边长的情况下，确定三角形的形状和大小。

asa证全等的方法

asa证全等的方法

asa证全等的方法
1. 内角相等法：如果两个三角形的对应内角相等，则这两个三角形全等。

2. AA相似度法：如果两个三角形两对对应角相等，则这两个三角形全等。

3. SSS全等法：如果两个三角形的三边对应相等，则这两个三角形全等。

4. SAS全等法：如果两个三角形的一边和与其所夹角分别相等，则这两个三角形全等。

5. ASA全等法：如果两个三角形的一角和与其两边相等，则这两个三角形全等。

6. AAS相似度法：如果两个三角形两对对应角相等且两边成比例，则这两个三角形全等。

12.2.3 三角形全等的判定ASA、AAS

12.2.3 三角形全等的判定ASA、AAS
符号语言：
B A Ｄ
C
Ｅ
Ｆ
在△ABC与△DEF中 AB=DE
∠Ｂ=∠Ｅ
BC=EF
∴△ABC≌△DEF（SＡS）
探究新知
如果给出三个条件画三角形，你能 说出有哪几种可能的情况？
①三角； ②三边；
③两边一角；
④两角一边。
两个三角形有两个角和一条边分别对应 相等，有几种情况？
① 角——边——角
②
角——角——边
①角边角：画出一个三角形，使它的两个角分 别是55°和45°，并且使这两个角的夹边的长度 为 5cm ，把你画的三角形与小组内画的进行比较， 它们一定全等吗？ 画法: 1.画线段AB=5㎝; 2.以AB为角的始边,A为顶点，画一个55° 的角，再以B为顶点画一个45°的角； 3. 这两个角的终边相交于点Ｃ.
12.2.3
三角形全等的
判定(三)
课件制作
管 斌
判定一：三边对应相等的两个三角形全等 （简写为：SSS）
用符号语言进行表述：
在△ABC与△DEF中 AB=DE A B C E D F
AC=DF
BC=EF
∴△ABC≌△DEF（SSS）
判定二：两边和它们的夹角对应相等的两 个三角形全等. 可简写为边角边或SAS
结论:两角和它们的夹边对应相等的两个 三角形全等. 判定三：可简写为角边角或ASA
判定三：两角和它们的夹边对应相等的两 个三角形全等. 可简写为角边角或ASA
符号语言：
B A Ｄ
C
Ｅ
Ｆ
在△ABC与△DEF中 ∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF（ASA）
例1.如图，点D在AB上，点E在AC上，AB=AC， ∠B=∠C，求证：AD=AE. 证明：在△ABE和△ACD中

全等三角形判定(ASA和AAS)

全等三角形判定(ASA和AAS)
∴ ∠B=∠DEF , ∠ACB=∠F
在△ABC和△DEF中
∠B=∠E BC=EF ∠C=∠F ∴△ABC≌△DEF（ASA）
你能行吗?
× AB=DE可以吗？
B A
C
F
D E
1、如图∠ACB=∠DFE， BC=EF，那么应补充一个条 件 ------------------------- ，才 能使△ABC≌△DEF （写出 一个即可）。
为两角夹边
B
C 图2
在图2中， 边BC是∠A的对 边， 我们称这种位置关系为
两角及其中一角的对边。
二、合作探究
（一）探究一：已知两个角和一条线段，以这 两个角为内角，以这条线段为这两个角的夹边， 画一个三角形．
45°
3 cm
30°
把你画的三角形与小组其他组员画的三角形进
行比较，所有的三角形都全等吗？ 都全等
利用“角怎边么角办？定可理以”帮帮可知,带B
A
块去，可以配我到吗？一个与原来全
等的三角形玻璃。
B
考考你
1、如图，已知AB=DE， ∠A =∠D， ,∠B=∠E，则 △ABC ≌△DEF的理由是： 角边角（ASA）
2、如图，已知AB=DE ,∠A=∠D，,∠C=∠F，则
△ABC ≌△DEF的理由是： 角角边（AAS）
Q AB AC
AB AD AC AE (等式的性质)
BD CE
3.已知ABC中，BE AD于E，CF AD于F，
且BE CF，那么BD与DC相等吗？
A
证明：Q BE AD，CF AD
BED CFD 90 (垂直的定义）
F
Q 在BDE和CDF中
B
D
C
BED CFD（已证）

人教版三角形全等的判定(ASA_AAS)

人教版三角形全等的判定(ASA_AAS)

over
例: 如图,O是AB的中点，∠A= ∠B， △AOC与△BOD全等吗?为什么？
两角和夹边 对应相等
C
A
O
B
解：在 DAO和 CDBOD中
D
A B(已知)
AOBO (中点的定义) AOCBO(D 对顶角相等)
\ DAOC DBOD (ASA)
例: 如图,O是AB的中点，∠C= ∠D，
A
A
B
C
B
C
探究5
先任意画出一个△ABC，再画一个 △A/B/C/，使A/B/=AB， ∠A/ =∠A， ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的 △A/B/C/剪下，放到△ABC上，它们全等吗？
C
A
B
已知：任意 △ ABC，画一个△ A/B/C/， 使A/B/＝AB， ∠A/ =∠A， ∠B/ =∠B ：
练一练：
1、如图∠ACB=∠DFE，BC=EF，根据SAS,ASA或AAS，
那么应补充一个直接条件
AC=DF或∠B=∠E或∠A=∠D
--------------------------，
（写出一个即可），才能使△ABC≌△DEF.
A
A
F
E
B
C
D
E
1
2
D
B
C
2、如图，BE=CD，∠1=∠2，则AB=AC吗？为什么？
∠A=∠A（公共角） AC=AB（已知） ∠C=∠B（已知）
D
E
O
∴△ACD≌△ABE（ASA）
B
C
∴AD=AE（全等三角形的对应边相等）
又∵AB=AC（已知）
∴BD=CE
(2) (1)

三角形全等的判定(AAS、ASA)课件

三角形全等的判定(AAS、ASA)课件
（2）两角分别相等且其中一组等角的对边相等 的两个三角形全等（AAS）.
A
∠F=180o - ∠D -∠E
C
又∵ ∠A=∠D， ∠B=∠E
∴ ∠C=∠F
B
D
在△ABC和△DEF中
∠B=∠E BC=EF ∠C=∠
必须是两角夹的一边才可以证明的两个三角形全等吗？ 你发现了什么？
A
结论：
有两个角和 其中一个角的对边 对应 相等的两个三角形全等。
三角形全等的判定
角边角（ASA）、角角边（AAS）
合作探究一：阅读课本P39探究4说出你的结论：
先任意画一个△ABC，再画一个△A'B'C'
使得A'B'=AB， ∠A' = ∠A ，∠B' = ∠B；E D
C
C'
A
B
A'
B'
画法： 1、画A'B'=AB 2、画∠A'= ∠A;再画∠B'= ∠B
A'D、B'E交于点C'
全等？ 1. 注意格式
2.字母对应
三角形全等判定方法3： 三角形全等判定方法4：
在ΔABC和ΔDEF中 ∠B=∠E
∵ BC= EF ∠C=∠F
在ΔABC和ΔDEF中 ∠B=∠E
∵ ∠C=∠F AC=DF
∴ΔABC≌DEF（ASA） A
∴ΔABC≌DEF （AAS） D
B
C
E
F
课堂小结
判断三角形全等的两个定理，它们分别是： （1）两角及其夹边分别相等的两个三角形全等 （ASA）
解：△AOC≌△BOD，理由如下：
∵点O是AB的中点

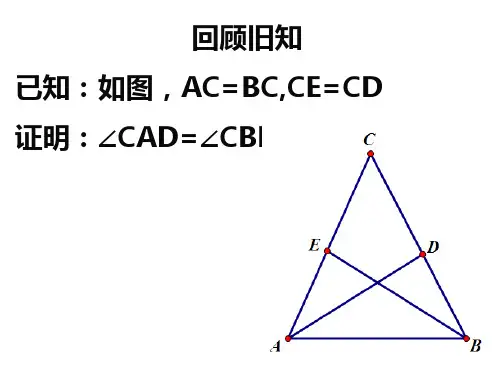
人教版八年级数学上册全等三角形的判定ASAAAS课件

人教版八年级数学上册全等三角形的判定ASAAAS课件
△ ABC ≌△ A ' B ' C ' ( ASA )
自学检测1（ASA） 《课本》 P41：练习2
自学探究2 【范围】P40例题4至最后 【时间】3分钟 【要求】 1、在图中标出已知的等边、等角 2、熟记得到的判定方法
三角形全等的判定（4）——AAS
两角和其中一个角的对边分别相等的两个三角 形全等
回顾旧知 已知：如图，AC=BC,CE=CD 证明：∠CAD=∠CBE
三角形全等的判定 （ASA AAS）
学习目标
1、探究并掌握两个三角形全等 的判定方法：“ASA”和 “AAS”
2、能灵活运用“ASA”和 “AAS”判定两个三角形全等
师生探究
有志者能使石头长出青草来。
1、任意画一个△ABC 鸭仔无娘也长大，几多白手也成家。
符号语言： 在△ ABC 与△ A ' B ' C '中
A A'
B
B'
AC A ' C '
△ ABC ≌△ A ' B ' C ' ( AAS )
自学检测2(AAS) 《课本》 P41：练习1
课堂小结
1、我们这节课学过的三角形的 两个判定方法有哪些？
2、归纳总结三角形全等的判定 方法。 “SSS”、”SAS”、 “ASA”、“AAS”
桐山万里丹山路，雄风清于老风声 大丈夫处世，不能立功建业，几与草木同腐乎? 大丈夫处世，不能立功建业，几与草木同腐乎? 古之立大事者，不惟有超世之材，亦必有坚忍不拨之志。
2、画一个△A’B’C’，使 志高山峰矮，路从脚下伸。
不怕路远，就怕志短。 鱼跳龙门往上游。
A’B’=AB，∠A’=∠A， 追踪着鹿的猎人是看不见山的。

12.2.3三角形全等的判定(三)AAS或ASA

12.2.3三角形全等的判定(三)AAS或ASA

湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——助您成功
前 言 高考状元是一个特殊的群体，在许
多人的眼中，他们就如浩瀚宇宙里璀璨夺 目的星星那样遥不可及。但实际上他们和 我们每一个同学都一样平凡而普通，但他 们有是不平凡不普通的，他们的不平凡之 处就是在学习方面有一些独到的个性，又 有着一些共性，而这些对在校的同学尤其 是将参加高考的同学都有一定的借鉴意义。
湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——助您成功
青 春 风 采
湖北鸿鹄志文化传媒有限公司——助您成功
高考总分：
692分(含20分加分) 语文131分 数学145 分英语141分 文综 255分
毕业学校：北京二中 报考高校： 北京大学光华管理学 院 北京市文科状元 阳光女孩--何旋 湖北鸿鹄志文化传媒有限公司——助您成功
在图2中， 边BC是∠A的对 边， 我们称这种位置关系为两 角及其中一角的对边。
观察下图中的△ABC，画一个△A B C ′ ，使 A B ′′ =AB , ∠′ A′ = ∠A ， ′ ∠B = ∠B ′
′ A B =AB； ′ 画法: 1. 画 ′′ ′′ ′′ 2.在A B 的同旁画∠DA B = ∠A ,∠EB A = ∠B, ′′ ′ ′ E D A D、B E交于点C C C′ B A′ 观察：△A B′ C′ 与 △ABC 全等吗？怎么验证？ ′ 思考：这两个三角形全等是满足哪三个条件？ 结论:两角及夹边对应相等的两个三角形全等(ASA). A
∠C=∠F A D
BC=EF B ∴△ABC≌△DEF（SAS）
C F E
一张教学用的三角形硬纸板不小心被撕坏 了，如图，你能制作一张与原来同样大小的新 教具？能恢复原来三角形的原貌吗？

三角形全等的判定(ASA、AAS)

三角形全等的判定(ASA、AAS)
在△ABC和△DEF中
A D
∠A=∠D
AB=DE ∠B=∠E
B
C F E
∴ △ABC≌△DEF（ASA）
如图，应填什么就有 △AOC≌ △BOD:
B
∠A=∠B,（已知）
AO=BO （已知） ,
C
1 2
∠1=∠2（对顶角相等）
∴△AOC≌△BOD (ASA)
A
O
D
小明踢球时不慎把一块 三角形玻璃打碎为两块,他是 否可以只带其中的一块碎片 到商店去,就能配一块于原来 一样的三角形玻璃呢?
等。(可以简写成“边角边”或“SAS”)
用符号语言表达为：
A D
在△ABC与△DEF中 AC=DF
∠C=∠F BC=EF
B
C F E
∴△ABC≌△DEF（SAS）
继续探讨三角形全等的条件： 两角一边
思考：已知一个三角形的两个角和一条边，那么两个角 与这条边的位置上有几种可能性呢？ A A
B
图1
C
B
练习:
三步走：
①要证什么；
②已有什么；
A
D
=
=
③还缺什么。
B
E C
F
大显身手
练习1：已知如图，AB⊥BC,AD⊥DC,垂足
分别为B、D，∠1=∠2，求证：AB=AD
证明：∵AB⊥BC，AD⊥DC ∴∠B＝∠D＝90° 在△ABC和△ADC中 ∠1＝∠2 ∠B＝∠D AC＝AC ∴△ABC≌△ADC（AAS） B ∴AB＝AD
C E ′ C D
A
B A ′
B′
观察：△A ′ B ′ C ′ 与 △ABC 全等吗？怎么验证？ 思考：这两个三角形全等是满足哪三个条件？

全等三角形判定(ASA和AAS)

全等三角形判定(ASA和AAS)

证明:在△ABC与△A B C 中
∠A=∠A
∴△ABC≌△A’B’C’（AAS）
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B C
判定3： 两角和它们的夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”。
判定4： 两角和其中一角的对边分别相等的两个三角形全等，简写成“角角边”或“AAS”
6、如图，AB∥CD，AD∥BC，那么AB=CD吗？为什么？AD与BC呢？
A
B
C
D
1
2
3
4
证明：∵ AB∥CD，AD∥BC（已知 ） ∴ ∠1＝∠2 ∠3＝∠4 （两直线平行，内错角相等） ∴在△ABC与△CDA中 ∠1＝∠2 （已证） AC=AC （公共边） ∠3＝∠4 （已证） ∴ △ABC≌△CDA（ASA） ∴ AB=CD BC=AD（全等三角形对应边相等）
03
02
01
如何用符号语言来表达呢?
证明:在△ABC与△A B C 中
∠A=∠A AB=A B
∴△ABC≌△A’B’C’（ASA）
A
C
B
A
′
C
B
′
′
′
′
′
′
′
′
∠B=∠B
′
两角和它们的夹边分别相等的两个三角形全等(ASA).
在△ABC和△DEF中， ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗？为什么？
A
C
A
B
C
图1
图2
在图1中， 边AB是∠A与∠B的夹边，

全等三角形的判定(AAS和ASA)

全等三角形的判定(AAS和ASA)

全等三角形的判定【知识梳理】1、三角形全等的条件(三)：两角和它们的夹边对应相等的两个三角形全等。

2、三角形全等的条件(四)：两个角和其中一个角的对边对应相等的两个三角形全等。

3、三个角对应相等的情形：三个角对应相等的两个三角形不一定全等。

4、三角形全等的条件的选用：要根据具体情况和题设条件确定，其基本思路见下表：已知条件可选择的判定方法一边一角对应相等SAS、AAS、ASA两角对应相等ASA、AAS两边对应相等SAS、SSS【例题精讲】【例1】如图⑴，AB=CD，AD=BC，O为AC的中点，过O点的直线分别与AD、BC相交于点M、N，那么∠1与∠2有什么关系？请说明理由。

若将过O点的直线旋转至图⑵、⑶的情况时，其他条件不变，那么图⑴中∠1与∠2的关系还成立吗？【变式1-1】如图，在△ABC中，AB⊥BC，AB=BC，D为AC上一点，AE⊥BE交BD的延长线于E，BE⊥CF 于F，求证：EF=CF-AE。

【变式1-2】如图，AD∥BC，AB∥DC，MN=PQ，求证：DE=BE。

【变式1-3】如图，在Rt△ABC中，AB=AC，∠BAC=90°，∠1=∠2，CE⊥BD的延长线于E。

求证：BD=2CE。

【变式1-4】如图①所示，OP是∠MON的平分线，请利用该图形画一对以OP所在直线为对称轴的全等三角形。

请你参考这个作全等三角形的方法，解答下列问题：⑴如图②，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F。

请你判断并写出FE与FD之间的数量关系；⑵如图③，在△ABC中，如果∠ACB不是直角，而⑴中的其他条件不变，请在⑴中所得结论是否仍然成立?若成立，请证明；若不成立，请说明理由。

【变式1-5】线段AC与BD相交于点O，连结AB、DC，E为OB的中点，F为OC的中点，连结EF(如图所示)。

⑴添加条件∠A=∠D，∠OEF=∠OFE。

人教版三角形全等的判定ASA、AAS

人教版三角形全等的判定ASA、AAS

∠C＝180° —∠A — ∠B
同理∠C′＝180°—∠A′—∠B′
又∵∠A＝∠A′，∠B＝∠B′
∴ ∠C＝∠C′．
在△ABC和△A′B′C′中
B
∠A＝∠A′
AC＝A′C′
∠C＝∠C′
∴△ABC≌△A′B′C′（ASA）
E
C D
F
例2.已知，如图，∠1=∠2，∠C=∠D
求证：AC=AD
证明：
D
∠3=∠4
情感态度与价值观
过过程 有意识地培养学生学习数学，初步形成与他人合作交流的意识的积极 性
重点： （ASA）判定定理的内容 难点
（ASA）判定定理的内容
探究1
先任意画出一个△ABC，再画一个 △DEF，使DE=AB， ∠D =∠A， ∠E =∠B (即使两角和它们的夹边对应相等)。 把画好的△DEF剪下，放到△ABC上， 它们全等吗？
C
A
B
画法： 1、画DE＝AB；
2、在 DE的同旁画∠MDE =∠A ，
∠NED=∠B， DM，EN交于点F。
N
M
C C′
A
B
D
E
通过实验你发现了什么规律？
探角究边反角映判的定规定律理是：
有两角和它们夹边对应相等的两个三 角形全等(简写成“角边角”或“ASA”）。
符号语言表示
A
在△ABC和△DEF中
12.2三角形全等的判定ASA、AA
1.什么是全等三角形？ 2.判定两个三角形全等方法有哪些?
边边边：
三边对应相等的两个三角形全等。
边角边：
有两边和它们夹角对应相等的两个
三角形全等。
教学目标
知识与智能
（ 掌握三角形全等的判定定理 ASA）

三角形全等的判定三AAS、ASA(课件)

三角形全等的判定三AAS、ASA(课件)
证明：在△ABC中，∠A+∠B+∠C=180°，
∴∠C=180°-∠A-∠B，
同理∠F=180°-∠D-∠E ， 又∵∠A=∠D，∠B=∠E ， ∴∠C=∠F ， 在△ABC和△DEF中，
B E
BC
EF
C F
∴△ABC≌△DEF (ASA).
★“角角边”判定方法
◆文字语言：两角分别相等且其中一组等角的对边相等的两个三角形全等. (可以简写成“角角边”或“AAS”). 几何语言：
5.如图，要测量池塘两岸相对的两点A，B的距离，可以在池塘外取AB的垂
线BF上两点C，D，使BC=CD，再画出BF的垂线DE，使E与A，C在一条直
线上，这时测得DE的长就是AB的长.为什么？
解：∵ AB⊥BF，DE⊥BF，
∴ ∠ABC=∠EDC=90° ， 在△ABC和△EDC中，
ABC EDC
1.如图，使△ABC≌△A′B′C′的条件是( B )
A.AB=A′B′，BC= B′C′ ，∠A=∠ A′
B.AB= A′B′ ，AC= A′C′ ，∠A=∠ A′
C.AB= A′B′ ，AC= A′C′ ，∠B=∠B′
D.AB= A′B′ ，BC= B′C′ ，∠C=∠ C′
2.如图，要使△ABC≌△DEF，已知∠A=∠D，∠C=∠F，则不能使之全
【分析】证明△ACD≌△ABE,就可以得出AD=AE.
证明：在△ACD和△ABE中，
A A
AC
AB
C B
∴ △ACD≌△ABE (ASA) ，
∴ AD=AE.
如图，AB⊥BC，AD⊥DC，垂足分别为B，D，∠1=∠2.求证AB=AD.
证明：∵ AB⊥BC，AD⊥DC，

全等三角形判定ASA和AAS经典实用

全等三角形判定ASA和AAS经典实用

如图,小明不慎将一块三角形模具打碎为两块,他是否可 以只带其中的一块碎片到商店去,就能配一块与原来一 样的三角形模具吗? 如果可以,带哪块去合适? 你能说明其中理由吗?
利用“角怎边么角办？定可理以”帮帮可知,带B
A
块去，可以配我到吗？一个与原来全
等的三角形玻璃。
B
•全等三角形判定(ASA和AAS)
CF
E
“AAS”）。
•全等三角形判定(ASA和AAS)
知识要点： (1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”. (2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”. （3）探索三角形全等是证明线段相等（对应边相等），
角相等（对应角相等）等问题的基本途径。
复习回顾：
我们前面学习了哪几种判定三角形全等的方法 SSS SAS
两边和它们的夹角对应相等的两个三角形全 等．（SAS）
•全等三角形判定(ASA和AAS)
继续探讨三角形全等的条件： 两角一边
思考：已知一个三角形的两个角和一条边，那么两个角
与这条边的位置上有几种可能性呢？

A
B 图1
C
在图1中， 边AB是∠A与∠B 的夹边，我们称这种位置关系
D
E
∠A= ∠A （公共角）
O
AE=AD （已知）
B
C ∴ △ABE ≌△ACD（AAS）
∴ BE=CD （全等三角形对应边相等）
•全等三角形判定(ASA和AAS)
例2. 如图,O是AB的中点，A= B， AOC与 BOD全等吗? 为什么？
C
两角和夹
边对应相
A
等
O
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

D
C A B F E
1.2三角形全等的判定（aas asa ）导学案
【学习目标】
1、掌握三角形全等的“角边角”“角角边”条件．能运用全等三角形的条件，解决简单的推理证明问题
2．经历探索三角形全等条件的过程，体会利用操作、•归纳获得数学结论的过程．
3、积极投入，激情展示，体验成功的快乐。

教学重点：已知两角一边的三角形全等探究．
教学难点：灵活运用三角形全等条件证明．
【学习过程】
一、自主学习
1、复习思考
（1）．到目前为止，可以作为判别两三角形全等的方法有几种？各是什么？
（2）．在三角形中，已知三个元素的四种情况中，我们研究了三种，今天我们接着探究已知两角一边是否可以判断两三角形全等呢？三角形中已知两角一边又分成哪两种呢？
2、探究一：两角和它们的夹边对应相等的两个三角形是否全等？
(1)动手试一试。

已知：△ABC
求作：△'''A B C ，使'B ∠=∠B, 'C ∠=∠C ，
''B C =BC ，（不写作法，保留作图痕迹）
(2) 把△'''A B C 剪下来放到△ABC 上，观察△'''A B C 与△ABC 是否能够完全重合？
(3)归纳；由上面的画图和实验可以得出全等三角形判定（二）：
两角和它们的夹边对应相等的两个三角形 （可以简写成“ ”或“ ”）
(4)用数学语言表述全等三角形判定（三） 在△ABC 和'''A B C ∆中,
∵'B B BC C ∠=∠⎧⎪=⎨⎪∠=⎩ ∴△ABC ≌
3、探究二。

两角和其中一角的对边对应相等的两三角形是否全等
（1）如图，在△ABC 和△DEF 中，∠A=∠D ，∠
B=∠E ，BC=EF ，△ABC 与△DEF 全等吗？能利C '
B 'A '
C B A
E O D C B A 用前面学过的判定方法来证明你的结论吗？
（2）归纳；由上面的证明可以得出全等三角形判定（四）：
两个角和其中一角的对边对应相等的两个三角形 （可以简写成“ ”或“ ”）
(3)用数学语言表述全等三角形判定（四） 在△ABC 和'''A B C ∆中,
∵'A A B BC ∠=∠⎧⎪∠=⎨⎪=⎩ ∴△ABC ≌
二、合作探究
1、例1、如下图，D 在AB 上，E 在AC 上， AB=AC ，∠B=∠C ．
求证：AD=AE ．
2．已知：点D 在AB 上，点E 在AC 上，∠BAO=∠CAO ,BE ⊥AC, CD ⊥AB,相交于点O ，AB=AC ， 求证：BD=CE
三、学以致用
1、课本第11页第1、2题
D C A B
E C '
B 'A '
C B A
2、如图，在△ABC中，∠C=2∠B,AD是△ABC的角平分线，∠1=∠B,求证AB=AC+AD
六、课堂小结
（1）今天我们又学习了两个判定三角形全等的方法是：
（2）三角形全等的判定方法共有
（3）会根据已知两角及一边画三角形
作业：。