高三数学三垂线定理

【教学目标】正确理解和熟练掌握三垂线定理及其逆定理，并能运用它解决有关垂直问题。

【知识梳理】 1．斜线长定理从平面外一点向这个平面所引的垂线段和斜线段中，①射影相等的两条斜线段相等，射影较长的斜线段也较长；②相等的斜线段的射影相等，较长的斜线段的射影也较长；③垂线段比任何一条斜线段都短． 2．重要公式 如图，已知OB ⊥平面α于B ，OA 是平面α的斜线，A 为斜足，直线AC ⊂平面α，设∠OAB =θ1，又∠CAB =θ2，∠OAC =θ．那么cos θ=cos θ1⋅cos θ2．3．直线和平面所成的角①平面斜线与它在平面内的射影所成的角，是这条斜线和这个平面内任一条直线所成的角中最小的角．②一个平面的斜线和它在这个平面内的射影的夹角，叫做斜线和平面所成的角(或斜线和平面的夹角)．如果直线和平面垂直，那么就说直线和平面所成的角是直角；如果直线和平面平行或在平面内，那么就说直线和平面所成的角是0︒的角．三垂线定理和三垂线定理的逆定理的主要应用是证明两条直线垂直，尤其是证明两条异面直线垂直，此外，还可以作出点到直线的距离和二面角的平面角．在应用这两个定理时，要抓住平面和平面的垂线，简称“一个平面四条线，线面垂直是关键”．【点击双基】1．下列命题中，正确的是 ( )(A )垂直于同一条直线的两条直线平行(B )平行于同一平面的两条直线平行(C )平面的一条斜线可以垂直于这个平面内的无数条直线(D )a 、b 在平面外，若a 、b 在平面内的射影是两条相交直线，则a 、b 也是相交直线2．直线a 、b 在平面α内的射影分别为直线a 1、b 1，下列命题正确的是 ( )(A )若a 1⊥b 1，则a ⊥b (B )若a ⊥b ，则a 1⊥b 1(C )若a 1//b 1，则a 与b 不垂直 (D )若a //b ，则a 1与b 1不垂直3．直线a 、b 在平面外，若a 、b 在平面内的射影是一个点和不过此点的一条直线，则a 与b 是 ( )(A )异面直线 (B )相交直线(C )异面直线或相交直线 (D )异面直线或平行直线4．P 是△ABC 所在平面外一点，若P 点到△ABC 各顶点的距离都相等，则P 点在平面ABC 内的射影是△ABC 的 ( )(A )外心 (B )内心 (C )重心 (D )垂心C αD A B OC A P BD M N Q l 5．P 是△ABC 所在平面外一点，若P 点到△ABC 各边的距离都相等，且P 点在平面ABC 内的射影在△ABC 的内部，则射影是△ABC 的 ( )(A )外心 (B )内心 (C )重心 (D )垂心6．P 是△ABC 所在平面外一点，连结P A 、PB 、PC ，若P A ⊥BC ，PB ⊥AC ，则P 点在平面ABC 内的射影是△ABC 的 ( )(A )外心 (B )内心 (C )重心 (D )垂心7．从平面外一点向这个平面引两条斜线段，它们所成的角为θ．这两条斜线段在平面内的射影成的角为α(90︒≤α<180︒)，那么θ与α的关系是 ( )(A )θ<α (B )θ>α (C )θ≥α (D )θ≤α8．已知直线l 1与平面α成30︒角，直线l 2与l 1成60︒角，则l 2与平面α所成角的取值范围是( )(A )[0︒,60︒] (B )[60︒,90︒] (C )[30︒,90︒] (D )[0︒,90︒]【典例剖析】例1．如果四面体的两组对棱互相垂直，求证第三组对棱也互相垂直．已知：四面体ABCD 中，AB ⊥CD ，AD ⊥BC ；求证：AC ⊥BD ；证法一：作AO ⊥平面BCD 于O ， 连OB 、OC 、OD ，∵AB ⊥CD ，∴OB ⊥CD ，同理，由AD ⊥BC 得OD ⊥BC ，∴O 是△BCD 的垂心，∴OC ⊥BD ，从而AC ⊥BD ．证法二：设AB =a ，AC =b ，AD =c ，则BC =b -a ，BD =c -a ，CD =c -b ，∵AB ⊥CD ，AD ⊥BC ，∴a ⋅(c -b )=0，c ⋅(b -a )=0，则a ⋅c =a ⋅b ，a ⋅c =c ⋅b ．∴a ⋅b =c ⋅b ，即a ⋅b -c ⋅b =0，从而有b ⋅(c -a )=0，故AC ⊥BD ．例2．如图，在三棱锥P -ABC 中，∠ACB =90︒，∠ABC =60︒，PC ⊥平面ABC ，AB =8，PC =6，M 、N 分别是P A 、PB 的中点，设△MNC 所在平面与△ABC 所在平面交于直线l ．(1)判断l 与MN 的位置关系，并进行证明； (2)求点M 到直线l 的距离．解：(1)l //MN ，证明如下： ∵M 、N 分别是P A 、PB 的中点，∴MN //AB ，MN ⊄平面ABC ，AB ⊂平面ABC ， ∴MN //平面ABC ．又∵MN ⊂平面MNC ，平面MNC 平面ABC =l ，∴MN //l ．(2)取AC 的中点Q ，连MQ ，则MQ //PC ，而PC ⊥平面ABC ，∴MQ ⊥平面ABC ．作QD ⊥直线l 于D ，连MD ，则MD ⊥直线l ．线段MD 的长即为M 到直线l 的距离．在Rt △ABC 中，可求得AC =43，∴QC =23．又MQ =21PC =3，∠QCD =30︒，∴QD =21QC =3． 于是 MD =22QD MQ +=23．例3.如图，P 是ΔABC 所在平面外一点，且PA ⊥平面ABC 。

9．3线面垂直、三垂线定理一、明确复习目标1．掌握直线与平面垂直的定义、判定定理、性质定理，能用文字、符号、图形规范表述.2．掌握三垂线定理及其逆定理3．通过线线垂直、线面垂直、面面垂直的转化提高化归转化能力.4．会求斜线与平面所成的角.二．建构知识网络1．直线和平面垂直定义：一条直线和一个平面内的任意一条直线都垂直.记作：a⊥α2．直线与平面垂直的判定方法：（1）判定定理：一条直线和一个平面内的两条相交直线都垂直，则则线垂直；（2）依定义，一般要用反证法；（3）和直线的垂面平行的平面垂直于直线；（4）面面垂直的性质.3．直线和平面垂直的性质定理: 垂直于同一个平面的两条直线平行.4．点到平面的距离、直线和平面的距离以及面面距离的求法：找出垂线段，在一个平面内求，或用等积法、向量法求，5．斜线、射影、直线和平面所成的角：定义——性质：从平面外一点向平面所引的垂线段和斜线段中（1）垂线段最短；（2）斜线段相等<=>射影相等；(3)斜线段较长（短）<=>射影较长（短）.6．三垂线定理：平面内的直线，如果和这个平面的一条斜线的射影垂直，那么它也和斜线垂直。

三垂线定理的逆定理：平面内的直线，如果和这个平面的一条斜线垂直，那麽它也和这条斜线的射影垂直用途：判定线线垂直=>线面垂直，二面角的平面角.三、双双基题目练练手1.已知a，b，c是直线，α，β是平面，下列条件中，能得出直线a⊥平面α的是（）A.a⊥c,a⊥b，其中b⊂α,c⊂αB.a⊥b,b∥αC.α⊥β，a∥βD.a∥b,b⊥α2.如果直线l⊥平面α，①若直线m⊥l,则m∥α；②若m⊥α,则m∥l；③若m∥α,则m⊥l；④若m∥l,则m⊥α,上述判断正确的是（）A .①②③B .②③④C .①③④D .②④3.直角△ABC 的斜边BC 在平面α内，顶点A 在平面α外，则△ABC 的两条直角边在平面α内的射影与斜边BC 组成的图形只能是 （ ） A .一条线段 B .一个锐角三角形C .一个钝角三角形D .一条线段或一个钝角三角形4.已知P 为Rt △ABC 所在平面外一点，且P A =PB =PC ，D 为斜边AB 的中点，则直线PD 与平面ABC . （ ）A ．垂直B .斜交C .成600角 D .与两直角边长有关5．直线a ,b ,c 是两两互相垂直的异面直线，直线 d 是b 和c 的公垂线，则d 和a 的位置关系是______________. 6．（2006浙江）正四面体ABCD 的棱长为l ，棱AB ∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是______.◆答案提示：1-3.DBDA ; 5. a ∥d ;6. 21[,]42.CD ⊥平面α时射影面积最小42；CD //α时射影面积最大21.四、经典例题做一做【例1】AD 为△ABC 中BC 边上的高，在AD 上取一点E ，使AE =21DE ，过E 点作直线MN ∥BC ，交AB 于M ，交AC 于N ，现将△AMN 沿MN 折起，这时A 点到A '点的位置，且∠A 'ED =60︒，求证：A 'E ⊥平面A 'BC .【例2】如图，P 为△ABC 所在平面外一点，P A ⊥平 面ABC ，∠ABC =90°，AE ⊥PB 于E ，AF ⊥PC 于F ，求证： （1）BC ⊥平面P AB ； （2）AE ⊥平面PBC ； （3）PC ⊥平面AEF .ABCDMNA 'EA BP E F证明：（1）P A ⊥平面ABC ⇒ P A ⊥BCAB ⊥BCP A ∩AB =A （2）AE ⊂平面P AB ， 由（1）知AE ⊥BCAE ⊥PB PB ∩BC =B （3）PC ⊂平面PBC ， 由（2）知PC ⊥AE PC ⊥AF AE ∩AF =A【例3】如图，直三棱柱ABC -A 1B 1C 1中，∠ACB =90︒,AC =1,CB AA 1=1，侧面A A 1 B 1B 的两条对角线交于点D ，B 1C 1的中点为M ，求证：CD ⊥平面BDMMDA 1C 1B 1CBA证明：在直三棱柱111ABC A B C -中1CC AC ⊥，又90,ACB ∠= ∴AC ⊥平面1CB ，∵11AA =，1AC =∴1AC ∴1AC BC =， B A CD 1⊥ 连结1B C ，则111B C A B B C 是在面上的射影,也是CD 的射影 在1BB C ∆中，1tan BBC ∠在1BB M ∆中，1tan BMB ∠ ∴11BB C BMB ∠=∠, ∴1B C BM ⊥， ∴,CD BM BMBD B ⊥=，∴CD ⊥平面BDM .◆总结提练： 证线面垂直, 要注意线线垂直与线面垂直关系与它之间的相互转化 证线线垂直常用余弦定理、勾股定理逆定理,三垂线定理或通过线面垂直. 【例4】（2006浙江）如图，在四棱锥P ABCD -中，底面为直角梯形，//AD BC ，90BAD ∠=，⇒BC ⊥平面P AB . ⇒AE ⊥平面PBC . ⇒PC ⊥平面AEF .PA ⊥ 底面ABCD ，且2PA AD AB BC ===，M N 、分别为PC 、PB 的中点. （Ⅰ）求证：PB DM ⊥；（Ⅱ）求CD 与平面ADMN 所成的角. 解：（I ）∵N 是PB 的中点，PA PB =，∴AN PB ⊥. ∵AD ⊥平面PAB ，∴AD PB ⊥，从而PB ⊥平面ADMN . ∵DM ⊂平面ADMN ，∴PB DM ⊥.（II ）取AD 的中点G ，连结BG 、NG ，则//BG CD ， ∴BG 与平面ADMN 所成的角和CD 与面ADMN 所成的角相等.∵PB ⊥平面ADMN ，∴NG 是BG 在面ADMN 内的射影, BGN ∠是BG 与平面ADMN 所成的角. 在Rt BGN ∆中，sin BNBNG BG∠=故CD 与平面ADMN 所成的角是.五．提炼总结以为师1.熟练掌握线面垂直的判定定理及性质定理.2.证明线面垂直的常用方法： （1）用判定定理； （2）与直线的垂面平行（3）用面面垂直的性质定理； （4）同一法.（5）用活三垂线定理证线线垂直.3．线面角的求法：作出射影转化为平面内的角.同步练习 9.3线面垂直、三垂线定理【选择题】1.若两直线a ⊥b ，且a ⊥平面α，则b 与α的位置关系P N BC M DA是 （ ）A 、相交B 、b ∥αC 、b ∥α，或b ⊂αD 、b ⊂α 2.下列命题中正确的是 （ ） A .过平面外一点作这个平面的垂面有且只有一个 B .过直线外一点作这条直线的平行平面有且只有一个 C .过直线外一点作这条直线的垂线有且只有一条D .过平面的一条斜线作这个平面的垂面有且只有一个 3.给出下列命题：①若平面α的两条斜线段P A 、PB 在α内的射影长相等，那么P A 、PB 的长度相等；②已知PO 是平面α的斜线段，AO 是PO 在平面α内的射影，若OQ ⊥OP ，则必有OQ ⊥OA ；③与两条异面直线都平行的平面有且只有一个；④平面α内有两条直线a 、b 都与另一个平面β平行，则α∥β． 上述命题中不正确的是 （ ）A .①②③④B .①②③C .①③④D .②③④4.P A 垂直于以AB 为直径的圆所在的平面，C 为圆上异于A 、B 的任一点，则下列关系不正确的是 （ ）A P A ⊥BCB BC ⊥平面P AC C AC ⊥PBD PC ⊥BC 【填空题】5.△ABC 的三个顶点A 、B 、C 到平面α的距离分别为2 cm 、3 cm 、4 cm ，且它们在α的同侧，则△ABC 的重心到平面α的距离为______6. 在直四棱柱ABCD —A 1B 1C 1D 1中，当底面四边形ABCD 满足条件_______时，有A 1C ⊥B 1D 1（注：填上你认为正确的一种条件即可，不必考虑所有可能的情况）◆答案提示： 1-4 CDAC ； 5.3cm ; 6. AC ⊥BD 或四边形ABCD 菱形等; 【解答题】7．如图ABCD 是矩形，P A ⊥平面ABCD ，DP AD 是等腰三角形，M 、N 分别是AB 、PC 的中点，求证：MN ⊥平面PCD 证略8．（2006福建） 如图，四面体ABCD 中，O 、E 分别是BD 、BC 的中点，2,CA CB CD BD ====AB AD =（I ）求证：AO ⊥平面BCD ；（II ）求异面直线AB 与CD 所成角的大小；A B CD M N P（III ）求点E 到平面ACD 的距离.解法一：（I ）证明:证∠AOB =900. （II ）解：取AC 的中点M ，连结OM 、ME 、OE ，由E 为BC 的中点知ME ∥AB,OE ∥DC ∴直线OE 与EM 所成的锐角就是异面直线AB 与CD 所成的角.在OME ∆中，111,22EM AB OE DC === OM 是直角AOC ∆斜边AC 上的中线，11,2OM AC ∴==cos 4OEM ∴∠=AB 与CD所成角的大小为 （III ）等积法得1.CDE ACD AO S h S ∆∆∴== 即为所求.9.正方形ABCD 中，AB =2，E 是AB 边的中点，F 是BC 边上一点，将△AED 及△DCF 折起（如下图），使A 、C 点重合于A ′点.（1）证明：A ′D ⊥EF ；（2）当F 为BC 的中点时，求A ′D 与平面DEF 所成的角；（3）当BF =41BC 时，求三棱锥A ′—EFD 的体积.B EA B MDE O CF（1）证明：略（2）解：取EF 的中点G ，连结A ′G 、DG ………… 平面DEF ⊥平面A ′DG .作A ′H ⊥DG 于H ，得A ′H ⊥平面DEF ， ∴∠A ′DG 为A ′D 与平面DEF 所成的角. 在Rt △A ′DG 中，A ′G =22，A ′D =2， ∴∠A ′DG =arctan 42.(3)解：∵A ′D ⊥平面A ′EF ， ∴A ′D 是三棱锥D —A ′EF 的高. 又由BE =1，BF =21推出EF =25，可得S EF A '∆=45，V A ′－EFD =V D －A ′EF =31·S EF A '∆·A ′D=31·4510． 在直三棱柱ABC —A 1B 1C 1中，AB 1⊥BC 1，AB =CC 1=a ，BC =b . （1）设E 、F 分别为AB 1、BC 1的中点，求证：EF ∥平面ABC ； （2）求证：A 1C 1⊥AB ；（3）求点B 1到平面ABC 1的距离.AA C C11（11、BC 1的中点， ∴∥AC . ∴（2）证明：∵AB =CC 1，∴AB =BB 1.又三棱柱为直三棱柱，∴四边形ABB 1A 1为正方形.连结A 1B ，则A 1B ⊥AB 1. 又∵AB 1⊥BC 1，∴AB 1⊥平面A 1BC 1. ∴AB 1⊥A 1C 1. 又A 1C 1⊥AA 1，∴A 1C 1⊥平面A 1ABB 1. ∴A 1C 1⊥AB .（3）解：∵A 1B 1∥AB ，∴A 1B 1∥平面ABC 1.∴A 1到平面ABC 1的距离等于B 1到平面ABC 1的距离.过A 1作A 1G ⊥AC 1于点G ， ∵AB ⊥平面ACC 1A 1，∴AB ⊥A 1G .从而A 1G ⊥平面ABC 1，故A 1G 即为所求的距离，即A 1G =ab评述：本题（3）也可用等体积变换法求解.【探索题】（2004年春季上海）如下图，点P 为斜三棱柱ABC —A 1B 1C 1的侧棱BB 1上一点，PM ⊥BB 1交AA 1于点M ，PN ⊥BB 1交CC 1于点N .（1）求证：CC 1⊥MN ；（2）在任意△DEF 中有余弦定理：DE 2=DF 2+EF 2－2DF ·EFcos ∠DFE .拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明.1B （⊥PM ，CC 1⊥PN ，∴CC 1⊥平面PMN ⇒CC 1⊥MN .（2）解：S211ABB A 四边形=S211B BCC 四边形+S211A ACC 四边形 －2S 11B BCC 四边形·S 11A ACC 四边形cos α，其中α为平面CC 1B 1B 与平面CC 1A 1A 所成的二面角. ∵CC 1⊥平面PMN ，∴上述的二面角为∠MNP . 在△PMN 中, PM 2=PN 2+MN 2－2PN ．MNcos ∠MNP⇒PM 2CC 12=PN 2CC 12+MN 2CC 12－2（PN ·CC 1）·（MN ·CC 1）cos ∠MNP . ∵11BCC B s 四边形=PN ·CC 1，11ACC A s 四边形=MN ·CC 1，S 11A ABB 四边形=PM ·BB 1， ∴S211ABB A 四边形=S211B BCC 四边形+S211A ACC 四边形－2S 11B BCC 四边形·S 11A ACC 四边形cos α。

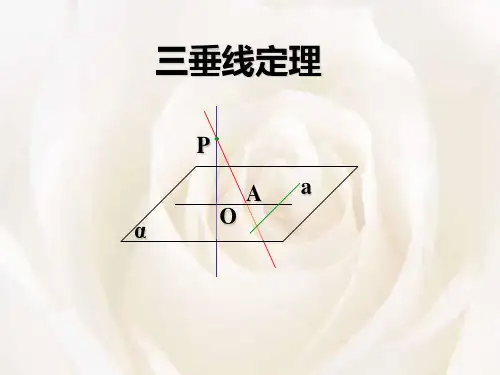
三垂线定理定义：在平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线在平面的射影垂直。

具体如下：1,三垂线定理描述的是PO(斜线),AO(射影),a(直线)之间的垂直关系.2,a与PO 可以相交,也可以异面.3,三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理.关于三垂线定的应用,关键是找出平面(基准面)的垂线.至于射影则是由垂足,斜足来确定的,因而是第二位的.从三垂线定理的证明得到证明a⊥b的一个程序:一垂,二射,三证.即第一,找平面(基准面)及平面垂线第二,找射影线,这时a,b便成平面上的一条直线与一条斜线.第三,证明射影线与直线a垂直,从而得出a与b垂直。

扩展资料：三垂线定理与逆定理的核心就是两两垂直。

其中射影就是斜线的一端到另一端到平面的垂线段的连线。

三垂线定理：影垂不怕线斜(形影不离)，即垂直射影垂斜线。

三垂线定理逆定理：斜垂影随其身(影随其身)，即:垂直斜线垂射影。

三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。

在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。

换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。

证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。

点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。

考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。

根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。

将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。

应用：利用三垂线定理，可以方便地计算三角形的面积。

设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。

由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。

三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。

需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。

三垂线定理在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直内心：三角形的三内角平分线交于一点。

（内心定理）外心：三角形的三边的垂直平分线交于一点。

（外心定理）中心：等边三角形的内心.外心.垂心.重心重合.则特指等边三角形的这个重合点垂心：三角形的三条高交于一点。

（垂心定理）重心：三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍。

（重心定理）重心：三角形重心是三角形三边中线的交点。

当几何体为匀质物体时，重心与形心（几何中心）重合。

1 重心的性质及证明方法1、重心到顶点的距离与重心到对边中点的距离之比为2：1。

证明一三角形ABC，E、F是AC，AB的中点。

EB、FC交于O。

证明：过F作FH平行BE。

∵AF=BF且FH//BE∴AH=HE=1/2AE（中位线定理）又∵ AE=CE∴HE=1/2CE∴FG=1/2CG（⊿CEG∽⊿CHF）2、重心和三角形3个顶点组成的3个三角形面积相等。

证明二证明方法：在△ABC内，三边为a，b，c，点O是该三角形的重心，AOA1、BOB1、COC1分别为a、b、c边上的中线根据重心性质知，OA1=1/3AA1，OB1=1/3BB1，OC1=1/3CC1过O，A分别作a边上高H1，H可知OH1=1/3AH 则，S(△BOC)=1/2×h1a=1/2×1/3ha=1/3S(△ABC)；同理可证S(△AOC)=1/3S(△ABC)，S(△AOB)=1/3S(△ABC) 所以，S(△BOC)=S(△AOC)=S(△AOB)3、重心到三角形3个顶点距离平方的和最小。

(等边三角形）证明方法：设三角形三个顶点为(x1,y1),(x2,y2),(x3,y3) 平面上任意一点为（x，y）则该点到三顶点距离平方和为：(x1-x)^2+(y1-y)^2+(x2-x)^2+(y2-y)^2+(x3-x)^2+(y3-y)^2=3x^2-2x(x1+x2+x3)+3y^2-2y(y1+y2+y3)+x1^2+x2^2+x3^2+y1^2+y2^2+y3^2=3(x-1/3*(x1+x2+x3))^2+3(y-1/3(y1+y2+y3))^2+x1^2+x2^2+x3^2+y1^2+y2^2+ y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2显然当x=(x1+x2+x3)/3,y=(y1+y2+y3)/3（重心坐标）时上式取得最小值x1^2+x2^2+x3^2+y1^2+y2^2+y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2 最终得出结论。

第5课时 三垂线定理1．和一个平面相交，但不和这个平面 的直线叫做平面的斜线，斜线和平面的交点叫做 ．2．射影1 平面外一点向平面引垂线的 叫做点在平面内的射影； 2 过垂足和斜足的直线叫斜线在平面内的 ． 斜线上任意一点在平面上的射影一定在 ． 垂线在平面上的射影只是 ．直线和平面平行时，直线在平面上的射影是和该直线 的一条直线． 3．如图，AO 是平面斜线，A 为斜足，OB⊥，B 为垂足，AC ，∠OAB＝，BAC ＝， ∠OAC＝，则co ＝ ． 4．直线和平面所成的角平面的斜线和它在这个平面内的 所成 的 叫做这条直线和平面所成角．斜线和平面所成角，是这条斜线和平面内任一条直线所成角中 ．5．三垂线定理：在平面内的一条直线如果和这个平面的一条斜线的 垂直，那么它也和 垂直．逆定理：在平面内的一条直线，如果和这个平面的一条 垂直，那么它也和这条 垂直．例1 已知RtABC 的斜边BC 在平面内，A 到的距离2，两条直角边和平面所成角分别是45°和30°．求：1 斜边上的高AD 和平面所成的角； 2点A 在内的射影到BC 的距离． 答案：1 60° 2变式训练1：如图，道旁有一条河，河对岸有电塔AB ，塔顶A 到道路距离为AC ，且测得∠BCA＝30°，在道路上取一点D ，又测得CD ＝30m ，∠CDB＝45°．求电塔AB 的高度． 解：BC ＝30，AB ＝BC tan30°＝10COBA例2．如图，矩形纸片A 1A 2A 3A 4，B 、C 、B 1、C 1 分别为A 1 A 4、A 2A 3的三等分点，将矩形片沿 BB 1，CC 1折成三棱柱，若面对角线A 1B 1BC 1； 求证：A 2CA 1B 1．解：取A 2B 1中点D 1 ∵A 2C 1＝B 1C 1 ∴C 1D 1⊥A 2B 1 又A 1A 2⊥面A 2B 1C 1 ∴C 1D 1⊥A 1A 2∴C 1D 1⊥面A 1A 2B 1B ∴BD 1是BC 1在面A 2B 上的射影 由A 1B 1⊥BC 1 ∴BD 1⊥A 1B 1取A 1B 中点D 同理可证A 2D 是A 2C 在面A 2B 上的射影 ∵A 2DBD 1 ∴A 2DBD 1是平行四边形 由BD 1⊥A 1B 1 ∴A 1B 1⊥A 2D ∴A 2C⊥A 1B 1变式训练2：如图，在正三棱柱ABC －A 1B 1C 1中，AB ＝3，AA 1＝4，M 为AA 1中点，的最短路线长，设这条最短路线与CC 1交点N ，求： 1 1C 1C 1C 1C 的最短路线 设1CA 1C 5211==AP C P MA NC 1C 1F 1F 1A 1F 1F 1F 1C221=CHCC 1C∥CC 1交BC 于M 则∴∠QBC BM BC BQ =1a aBC BM2=aa a BC CM22-=aa a AC CP22-=AC CPBC CM =∥AB在Rt△中a212-＝a 22∴tan∠Qaa 21222-⊥BC∴PQ⊥BC 又AD∥BC ∴PQ⊥AD例4．如图，在长方体ABCD －A 1B 1C 1D 1中，AD ＝AA 1＝1，AB ＝2，点E 在棱AB 上移动． 1 证明：D 1E⊥A 1D ；2 当E 为AB 的中点时，求点E 到面ACD 1的距离；3 AE 等于何值时，二面角D 1－EC －D 的大小为．1 证明：∵ AE⊥平面AA 1DD 1，A 1D⊥AD 1，∴A 1D⊥D 1E ．2 设点E 到面ACD 1的距离为h ，在△ACD 1中，AC ＝CD 1＝，AD 1＝，＝··215-＝，而＝·AE·BC＝． AACDBC ED BB 1A 1B CA 1A 2B 1C 1A 2C 1CBBE1∴ABC D V -1＝·DD 1＝·h ∴×1＝×h， ∴h＝3 过D 作DH⊥CE 于H ，连D 1H 、DE ，则D 1H⊥CE，∴∠DHD 1为二面角D 1－EC －D 的平面角．设AE ＝，则BE ＝2－在Rt△D 1DH 中，∵∠DHD 1＝，∴DH＝1∵在Rt△ADE 中，DE ＝21x +，∴在Rt△DHE 中，EH ＝，在Rt△DHC 中，CH ＝，CE ＝542+-x x ，则＋＝542+-x x ，解得＝2－．即当＝2－时，二面角为D 1－EC －D 的大小为．变式训练4：如图，在四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形，且PD ＝a ，PA ＝PC ＝a ． 1 求证：PD⊥面ABCD ； 2 求直线PB 与AC 所成角； 3 求二面角A －PB －D 大小． 证明：1 ∵PC＝a PD ＝DC ＝a ∴PD 2＋DC 2＝PC 2∴△PDC 是直角三角形 ∴PD⊥DC 同理PD⊥DA 又∵DA∩DC＝D ∴PD⊥平面ABCD2 连BD ∵ABCD 是正方形 ∴AC⊥BD 又∵PD⊥平面ABCD AC⊥PB 三垂线定理 ∴PB 与AC 所成角为90°3 设AC∩BD＝0 作AE⊥PB 于E ，连OE ∵AC⊥BD PD⊥平面ABCD AC 面ABCD ∴PD⊥AC ∴AC⊥平面PDB 又∵OE 是AE 在平面PDB 内的射影 ∴OE⊥PB∴∠AEO 就是二面角A －PB －O 的平面角 又∵AB＝a PA ＝ PB ＝∵PD⊥面ABCD DA⊥AB ∴ PA⊥AB 在Rt△PAB 中 AE·PB＝PA·AB ∴AE＝ AO ＝P ABCD∴in∠AEO＝∴∠AEO＝60°1．求直线和平面所成的角的一般步骤是一找作，二证，三算．寻找直线在平面内的射影是关键，基本原理是将空间几何问题转化为平面几何问题，主要转化到一个三角形内，通过解三角形来解决．2．三垂线定理及逆定理，是判定两条线互相垂直的重要方法，利用它解题时要抓住如下几个环节：一抓住斜线，二作出垂线，三确定射影．３．证明线线垂直的重要方法：三垂线定理及逆定理；线⊥面线⊥线；向量法．。

三垂线定理定义
三垂线定理：内切于一个三角形的三条垂线的交点，分别与三条边的中点构成的三角形，大小与原三角形相等。

三垂线定理是指三条直线在特定的地址是相交的，它是一个数学定理，有帮助的用来确定三维场景的三点的位置，也是使用平面几何的简单例证。

三垂线定理有着它自己独特的造诣，位置精度，并有助于建立地理图像的技术。

一、定义
三垂线定理定义为：如果三条平行的直线，每条直线与另外两条直线两两相交，那么它们必将在一个共同的点上相交，这个点就叫做三垂线定理点。

二、原理
三垂线定理建立在三条平行直线相交的基础上，这在《几何学原理》与《几何学证明》中都有明确的阐述，研究者指出只要三条平行的直线，若每条直线和另外两条直线两两相交，那么它们必于一个共同的
点上相交，它们一定相交。

三垂线定理有利于我们对三维场景中物体位置和形状的识别和定位，从而为图像分析和多视角显示技术提供了基础。

三、误差
由于三垂线定理受限于地理环境，地形因素和实际误差，误差不可避免。

在现实应用中，根据几何原理计算出的结果，最终的误差是受相对精度的影响，可能会大大影响定位的精度。

四、应用
三垂线定理的主要应用范围有三方面，一方面，它可以用来提高地理图像重建技术。

应用于有限空间中轨迹运动角度变化模拟，利用三垂线定理可以精确定位一定轨迹上的空间点。

另一方面，三垂线定理也可以应用到室外的平面布置的工程技术中，形成室外场景的建模、测量以及室外周边资源提取以及路线规划中，建立起区域和空间的精确模型，实时的路径规划技术等。

此外，三垂线定理在工业和医学图像采集/拍摄/控制等方面也有着广泛而重要的作用。