三垂线定理及其逆定理例题
知识点：
1.三垂线定理；；
2.三垂线定理的逆定理；
3.综合应用； 教学过程：
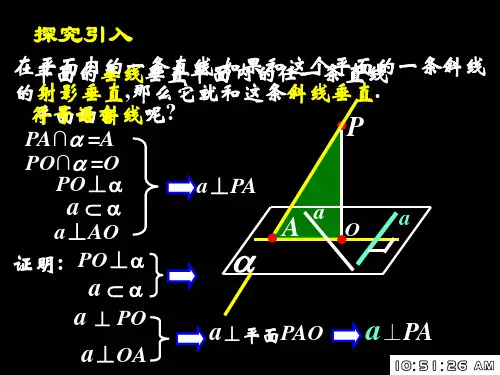
1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；
已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,,a α⊂a AO ⊥。 求证：a PO ⊥； 证明： 说明：
（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；
（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；
（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。 （4）直线a 与PO 可以相交，也可以异面。
（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。 例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。 求证：PC BC ⊥。
例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。 求证：,PO BD PC BD ⊥⊥。
P
B
B
例4.在正方体1AC 中，求证：1111
1,AC B D AC BC ⊥⊥；
2．写出三垂线定理的逆命题，并证明它的正确性； 命题： 已知： 求证： 证明： 说明：
例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。 求证：（1）AD BC ⊥；
（2）点A 在底面BCD 上的射影是BCD ∆的垂心；
P
D
A
B C
1
A C
例 3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上 已知： 求证：
说明：可以作为定理来用。
例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3
PAB PAc π
∠=∠=。
(1)求PA 与面ABC 所成的角的大小;
(2)当PA 的长度等于多少的时候，点P 在平面ABC 内的射影恰好落在边BC 上；
B
作业：
1.正方体1111D C B A ABCD -,,E F 分别是1,A A AB 上的点,1EC EF ⊥. 求证: 1EF EB ⊥。
2.已知：PA ⊥平面PBC ，,PB PC M =是BC 的中点。
求证：BC AM ⊥；
3.填空并证明： （1）在四面体ABCD 中，对棱互相垂直，则A 在底面BCD 上的射影是底面BCD 的 心。
（2）在四面体ABCD 中，AB 、ＡＣ、ＡＤ互相垂直，则A 在底面BCD 上的射影是底面BCD 的 心
（3）在四面体ABCD 中，AB=AC=AD ，则A 在底面BCD 上的射影是底面BCD 的 心。 （4）在四面体ABCD 中，顶点A 到BC 、CD 、DB 的距离相等，则A 在底面BCD 上的射影是底面BCD 的 心。
4.正方体1111D C B A ABCD -中棱长a ，点P 在AC 上，Q 在BC 1上，AP ＝BQ ＝a ， （1）求直线PQ 与平面ABCD 所成角的正切值； （2）求证：PQ⊥AD ．
5.在正方体1111D C B A ABCD -中，设E 是棱1AA 上的点，且1:1:2AE EA =，F 是棱AB 上的点，
12
C EF π
∠=
。求AF ：FB 。
6.点P 是ABC ∆所在平面外一点，且PA ⊥平面ABC 。若O 和Q 分别是ΔABC 和ΔPBC 的垂心，试证：OQ ⊥平面PBC 。
7.已知EAF ∠在平面α内，,,AT P PAE PAF αα⊂∉∠=∠，,,EAT FAT PD D αα∠=∠⊥∈。求证：D AT ∈；
A
B
