当前位置：文档之家 › 三垂线定理

三垂线定理

  • 格式：doc
  • 大小：83.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

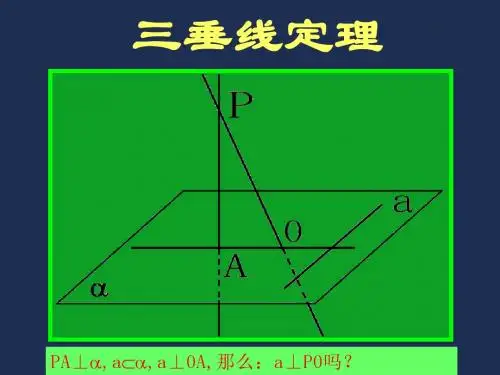
三垂线定理

三垂线定理

1. 在正方体AC1中,E,G分别是AA1和 是 所 1 P CC1的中点, F在AB上,且C1E⊥EF, PD 成 AB 则EF与GD所成的角的大小为( D ) 边 的 上 (A) 30° (B) 45° (C) 60°(D) 90° 角 的 D1 是 一 C1 EB1是EC1在平面AB1 EC AB 多 点 内的射影 A1 少 求 B1 G ? 异 EB1 ⊥EF E D 面 M C DG‖AM‖EB1 直 EF ⊥DG A 线 B F B1C
F D O B E
C
思考题:在四面体ABCD中,已知 ⊥CD, 思考题:在四面体 中 已知AB⊥ , AC⊥BD,求证:AD⊥BC 求证: ⊥ ⊥ 求证 证明: 于点O, 证明:作AO⊥平面 ⊥平面BCD于点 , 于点 连接BO, , 连接 ,CO,DO,则BO, , , A CO,DO分别为 ,AC, 分别为AB, , , 分别为 AD在平面 在平面BCD上的射影. 上的射影. 在平面 上的射影 ∵AB⊥CD,∴BO⊥CD, ⊥ , ⊥ , 同理CO⊥BD, ⊥ , 同理 的垂心, 于是O是 于是 是△BCD的垂心, 的垂心 ∴DO⊥BC,于是 ⊥BC. ⊥ ,于是AD⊥ B O C D
例2 如果一个角所在平面外一点到角 的两边距离相等, 的两边距离相等,那么这一点在平面 上的射影在这个角的平分线上. 上的射影在这个角的平分线上.
四,两个重要结论
练.(1)已知四面体 ( )已知四面体P-ABC, PA,PB,PC两两垂直,求证: 两两垂直, , , 两两垂直 求证: P在平面 在平面ABC内的射影是 在平面 内的射影是 A △ABC的垂心. 的垂心. 高的交点) (高的交点)
五,知识方法总结
1,三垂线定理及逆定理. 三垂线定理及逆定理. 作用:用于证明线线垂直. 2,作用:用于证明线线垂直. 用法:先找线面垂直, 用法:先找线面垂直,再找线射 垂直,从而推出线斜( (斜)垂直,从而推出线斜(射) 垂直. 垂直.平面可能水平放置也可能竖 直或倾斜放置. 直或倾斜放置. 3,两个射影结论. 两个射影结论.

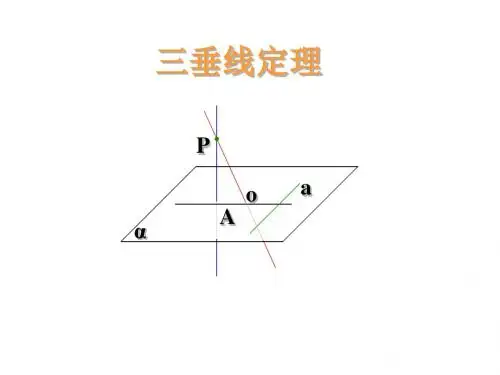
三垂线定理和逆定理

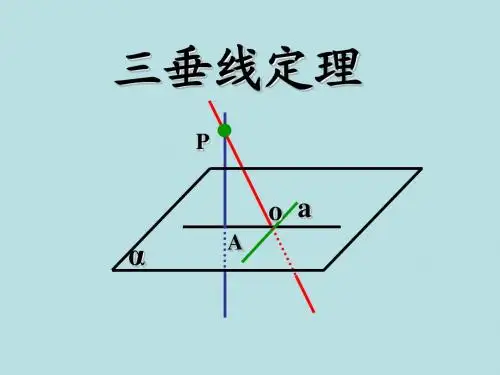
三垂线定理和逆定理

O
C
同理，AC⊥BD
平面ABCD
AC是PC在ABCD上的射影
∴ PC⊥BD
∴ PO⊥BD
P
(2) 已知：PA⊥平面PBC，PB=PC，
M是BC的中点， 求证：BC⊥AM 证明: ∵ PA⊥平面PBC
C A
∴ PM是AM在平面PBC上的射影
∵ PB=PC
M B
M是BC的中点
∴ PM ⊥BC 又 BC 平面PBC ∴ BC⊥AM
O
a
α
A
三垂线定理
说明：
1、三垂线定理描述的是PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 2、a与PO可以相交，也可以异面。 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。
例1 直接利用三垂线定理证明下列各题：
(1) 已知：PA⊥正方形ABCD所在平面，O为对角线BD的中点 求证：PO⊥BD，PC⊥BD (2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点， 求证：BC⊥AM
C
我们要学会从纷繁的已知条件中找出 或者创造出符合三垂线定理的条件 P
解 题 回 顾
α
A1
A
O
a
α
P
A O
a
P
B1
C1 A M B C
C B
三垂线定理解题的关键：找三垂！
解 题 回 顾
怎么找？
一找直线和平面垂直 二找平面的斜线在平面 内的射影和平面内的 一条直线垂直 P
α
A
O
a
注意：由一垂、二垂直接得出第三垂 并不是三垂都作为已知条件
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC， PO⊥ ，垂足分别是E、F、O，PE=PF P 求证：∠BAO=∠CAO 分析： 要证 ∠BAO=∠CAO 只须证OE=OF, OE⊥AB,OF⊥AC

【数学课件】三垂线定理

【数学课件】三垂线定理

E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
证明：∵AC面，a 面
∴ACa
一、三垂线定理
1.三垂线定理：在平面内的一条直线，如果和这个平面的一条 A 斜线的射影垂直，那么它也和这条斜线垂直。
已知：AC和AB分别是平面的垂
线和斜线，BC是AB在平面
C
B
a
上的射影，a，aBC。 求证： aAB。
证明：∵AC面，a 面
∴ACa
∵BCa ，AC∩BC＝C
9.4 直线与平面垂直的判定和性质
————————————————————— —
§6 三垂线定理
教学目的
• 掌握三垂线定理及逆定理 • 运用三垂线定理及逆定理解决数学问题 • 在实际生活中运用三垂线定理及逆定理
重点与难点
•三垂线定理及逆定理的适用条件 •三垂线定理及逆定理的应用

三垂线定理

三垂线定理
三垂线定理
P
o a
α
A
一、三线概念: 平面的斜线、垂线、射影 如图PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; o
α
AO是PO在平面
α内的射影.
已知:如图,PO为平面α 的斜线,PA⊥α ,a在平 面α内且垂直PO 的射影AO. 求证:a⊥PO
P a α
A
o
已知:如图,PO为平面α的斜线, PA⊥α ,a在平面α内且垂直PO 的射影AO.求证:a⊥PO P a 证明: A o PA⊥α 线线垂直 α PA⊥a a α 线面垂直 AO ⊥ a 线面垂直 a⊥平面PAO
1 1
D1
C1
四、小
结
三垂线定理：在平面内的一条直线，如 果和这个平面的一条斜线的射影垂直， 那么它也和这条斜线垂直。
1.定理中四条线均针对同一平面而言,
2.定理的主要应用:证明线线垂直, 线面垂直, 3.证明程序分三个步骤:“一垂二射三证”
计算程序分三个步骤:“一作二证三算”
∴ DC为PC在平面的射影,
而△ABC为等腰三角形, D为AB的中点, ∴ AB ⊥ CD
P C
∴ AB ⊥PC A
D
B
例2.如图，已知正方体ABCD-A1B1C1D1中， 连结BD1，AC，CB1，B1A， 求证：BD1⊥平面AB1C
证明：连结BD、 A1B ∵DD1⊥平面ABCD A B ∴BD是斜线D1B在平面ABCD 上的射影 ∵ABCD是正方形 D C ∴AC⊥BD (AC垂直射影BD)， B A ∴AC⊥BD1 同理:BA1是斜线BD1在平面ABB1A1上的射 影 , AB1 ⊥ BD1而AC ∩AB1 =A ∴BD1⊥平面AB1C

三垂线定理应用

三垂线定理应用
器和皮尺作测量工具，能否求出电塔顶与道路的距离？ 解：在道边取一点C， 使BC与道边所成水平角等于90°， 再在道边取一点D， 使水平角CDB等于45°， 测得C、D的距离等于20cm A
B
90°
C
45°
D
三垂线定理
∵BC是AC的射影
且CD⊥BC
∴CD⊥AC
因此斜线AC的长度就是电塔顶与道路的距离。 ∵∠CDB=45°，CD⊥BC，CD=20cm 答：电塔顶与道路的距离是25m。
三垂线定理：在平面内的一条直线，如果它和这个平 面的一条斜线的射影垂直，那么它也和这条斜线垂直。 已知:PO,PA分别是平面α的垂线,斜线,OA是PA 在 α内的射影,a 求证: a ⊥PA. α,且a ⊥OA.
P
A a O α

三垂线定理的逆定理：在平面内的一条直线，如果 它和这个平面的一条斜线垂直，那么它也和这条斜 线在平面内的射影垂直。
A
B∴BC=20m， Nhomakorabea在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm)
90°
C
45°
D
证明:∵AH⊥平面BCD，
A
∴BH为斜线AB在
平面BCD上的射影. B ∵AB⊥CD.
∵CD 平面BCD，
D
H C
∴BH⊥CD.
4、在空间四边形ABCD中AB⊥CD, AC⊥BD, A 求证:BC⊥CD
.
B
D
C
二、应用:
1、有一方木料如图,上底 有一点E,要经过点E在上底 面内画一条直线和C,E的连 线垂直,应怎样画?
“一垂二射三证明” “一垂”:找平面及平面的垂线 “二射”:找斜线在平面上的射影 “三证明”:用定理证明直线垂直

高中数学课件 三垂线定理

高中数学课件 三垂线定理

a⊥b。
( ×)
(2)若a是平面α的斜线，b是 平面α内的直线，且b垂直于a 在β内的射影，则a⊥b。（×）
P
a Ao
α
强调：1°四线是对同一个平面 而言.
2°定理的关键找“平面的垂线”.
例1 已知P 是平面ABC 外一点， PA⊥平面ABC ，AC ⊥ BC， 求 证： PC ⊥ BC P
A
O
注意：如果将定理中“在平面内” 的条件去掉，结论仍然成立吗？
解
直线a 在一定要在平面内，如果 a 不在平面内，定理就不一定成题 立。 回 NhomakorabeaP
b
顾
Oa
αA
练习３、 已知：PA⊥平面PBC， PB=PC， M是BC的中点，
求证：BC⊥AM P
C A
M B
练习４、 在正方体AC1中，
求证：A1C⊥BC1 ， A1C⊥B1D1
三垂线定理
在平面内的一条直线，如
果和这个平面的一条斜线的 射影垂直，那么，它就和这 条斜线垂直。 P
O
Aa
三垂线定理的逆定理
在平面内的一条直线，如
果和这个平面的一条斜线垂直，
那么，它也和这条斜线的射影
垂直。
P
O
Aa
1、判定下列命题是否正确
(1)若a是平面α的斜线、直线
b垂直于a在平面α内的射影，则
已知AB⊥CD、AC⊥BD求证：
AD⊥BC
A
B
D
O
作业：如图，已知正方体
AA平BC面，CDAC-BBA111C，B1CB11DA1，中D1求，证连：结CBB1DD11⊥，
A1
B1
D
A
C
B
再见！

三垂直定理立体几何

三垂直定理立体几何

三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。

在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。

换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。

证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。

点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。

考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。

根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。

将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。

应用：利用三垂线定理，可以方便地计算三角形的面积。

设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。

由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。

三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。

需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。

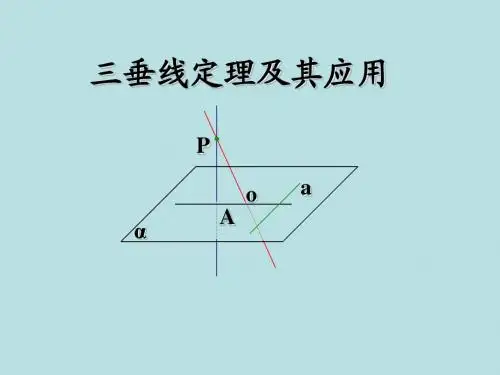
三垂线定理

三垂线定理

NO.*垂线定理三垂线定理在平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

1, 三垂线定理描述的是PO（斜线）,A0（射影）,a（直线）之间的垂直关系.2, a与P0可以相交，也可以异面.3, 三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理关于三垂线定理的应用，关键是找出平面（基准面）的垂线. 至于射影则是由垂足，斜足来确定的，因而是第二位的.从三垂线定理的证明得到证明a丄b的一个程序：一垂，二射，三证.即第一,找平面（基准面）及平面垂线第二，找射影线，这时a,b便成平面上的一条直线与一条斜线.第三，证明射影线与直线a垂直，从而得出a与b垂直.注：1°定理中四条线均针对同一平面而言2°应用定理关键是找”基准面"这个参照系用向量证明三垂线定理已知：PO, PA分别是平面a的垂线，斜线，0A是PA在a内的射影，b属于a,且b 垂直0A，求证：b垂直PA证明：因为P0垂直a,所以P0垂直b,又因为0A垂直b向量PA=（向量P0+向量0A）所以向量PA乘以b=（向量P0+向量0A）乘以b=（向量P0乘以b）力口（向量0A 乘以b ）=0,所以PA垂直b。

2）已知：P0, PA分别是平面a的垂线，斜线，0A是PA在a内的射影，b属于a,且b垂直PA,求证：b垂直0A证明：因为P0垂直a,所以P0垂直b,又因为PA垂直b,向量0A=（向量PA-向量P0）所以向量0A乘以b==（向量PA-向量P0）乘以b=（向量PA乘以b ）减（向量P0 乘以b ）=0,所以0A垂直b o 求交线0A于平面0BC所成的角。

2。

已知三个平面0AB , 0BC, 0AC相交于一点0，角A0B=角B0C=角C0A=6O 度,向量0A=（向量0B+向量AB） , 0是内心，又因为AB=BC=CA ,所以0A于平面0BC所成的角是30 度o.面角的求法有六种：1•定义法2•垂面法3•射影定理NO.*4•三垂线定理5•向量法6•转化法二面角一般都是在两个平面的相交线上，取恰当的点，经常是端点和中点。

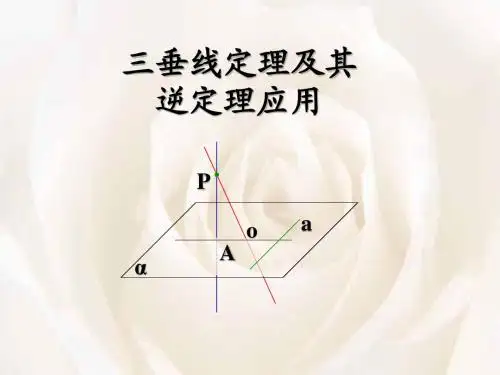
三垂线定理及其逆定理的应用

三垂线定理及其逆定理的应用
三垂线定理及其 逆定理应用
P
o
α A
a
复习：
三垂线定理：
在平面内的一条直线，如果和这个平面的一条斜线 的射影垂直，那么它也和这条斜线垂直。
三垂线定理的逆定理：
在平面内的一条直线，如果和这个 平面的一条斜线垂直，那么它也和 这条斜线的射影垂直。
P o a
α 三垂线定理及其逆定理可表述为：
A
设l 为平面α的斜线， l ′是l 在平面α内的射影， 直线a α ，则 a ⊥ l ′ a⊥l。
例3、把一个直角∠AOC按它的角平线OB折 叠，使OC在平面AOB上的射影为OB，则折后 ∠AOC等于多少？
P
θ1 θ2
C
O
θ
D
B
α
E A
600
例 4 ABCD 是矩形， 过 CD 的平面交 （ 1）求证：
PA 面 ABCD ，
PA ， PB 于 E 、 F ，
CDEF 是直角梯形；
例⒈ 已知PD⊥平面ABCD，下列条件中 ⑴ 四边形ABCD是菱形； ⑵ 四边形ABCD是矩形； ⑷若四边形ABCD是矩形， 且PD = a ，AB = b,BC = c， 求P到AB及AC的距离。 ⑵⑶ ⑴⑶
2 2
⑶ 四边形ABCD是正方形。
能使BC ⊥PC一定成立的序号有 能使AC ⊥PB一定成立的序号有 P
三垂线定理的逆定理：在平面内的一条直线，如果和这个
1°定理中四条线均针对同一平面而言
2°应用定理关键是找“基准面”这个参照系 3°操程序分三个步骤——“一垂二射三证”
两定理特征：四线一面三垂直
（ 2）当 PA AB a ， BC b ， E 、 F 分别是 PA 、 PB 的中点，且梯形的面积 是矩形面积的 5 4 时，求 a ： b 的值。

三垂线定理

三垂线定理
A D B C
同理:BA1是斜线BD1在平面ABB1A1上的射影 , AB1 ⊥ BD1 而AC ∩AB1 =A ∴BD1⊥平面AB线，如果
和这个平面的一条斜线的射影垂直，那么它也
和这条斜线垂直。
1.定理中四条线均针对同一平面而言,
2.定理的主要应用:证明线线垂直,线面垂直, 求点到线的距离,二面角大小, 3.证明程序分三个步骤:“一垂二射三证”, 计算程序分三个步骤:“一作二证三算”.
A D B
∴ AB ⊥ CD ∴ AB ⊥PC
例2.如图，已知正方体ABCD-A1B1C1D1中，连结
BD1，AC，CB1，B1A，求证：BD1⊥平面AB1C
证明：连结BD、 A1B
∵DD1⊥平面ABCD
A1 D1 B1 C1
∴BD是斜线D1B在平面ABCD上的射影
∵ABCD是正方形∴AC⊥BD (AC垂直射影BD)，∴AC⊥BD1
平面内的一条直线垂直的判定定理.
4 、转化思想:空间两直线的垂直问题转化为平面内 P 两直线的垂直问题.
α
A
o
a
练习：判定下列命题是否 正确
P A o a
α
(1)若a是平面α 的斜线、直线b垂直于a在平面
α 内的射影，则a⊥b。 且b垂直于a在β 内的射影，则a⊥b。 强调：1°四线是对同一个平面而言.
P a α A o
证明:
PA⊥α a α
PA⊥a ② a⊥平面PAO AO⊥a
PA∩AO=A
①
③
PO 平面PAO
②
线面垂直 ③
a⊥PO
线线垂直
① 线面垂直
线线垂直
性质定理
判定定理
性质定理
说明：

三垂线定理

三垂线定理

三垂线定理包含三种垂直关系
①线面垂直 ②线射垂直 ③线斜垂直
三垂线定理包含三种垂直关系 ①线面垂直
P
A
O
a
α
直线和平面垂直 和平面
三垂线定理包含三种垂直关系 ②线射垂直
P
A
O
a
α
平面内的直线和平面一条斜线的射 平面内的直线和平面一条斜线的射影垂直
三垂线定理包含三种垂直关系 ③线斜垂直
P
A
O
a
三垂线定理的证明
已知平面α 已知平面α， 斜线OP穿过平面α, 斜线OP穿过平面α, OP穿过平面 并交α 并交α于O点， a是α内一条直线， 内一条直线， 过P点作PA⊥ α ， 点作PA⊥ PA 连接OA, 连接OA, OA即OP在平面α内的射影, OA即OP在平面α内的射影, 在平面 若ＯＡ⊥ａ， ＯＡ⊥ 证明： 证明： OP ⊥ａ．
P O
A
a
α
三垂线逆定理的证明
P O 解：证明： 证明： ∵PA ⊥α ∴PA ⊥ a 又a ⊥ OP，且OP∩PA=P OP， a⊥平面 平面POA ∴a⊥平面POA ∴a ⊥ OA
A
a
α
逆定理：在平面内的一条直线， 逆定理：在平面内的一条直线，如 果和这个平面的一条斜线垂直， 果和这个平面的一条斜线垂直，那 它也和这条斜线的射影垂直。 么，它也和这条斜线的射影垂直。
定理内容阐述
1、三垂线定理包括5个要素： 三垂线定理包括5个要素：
一面(垂面) 四线（斜线、垂线、射影和平面内的直线） 一面(垂面)，四线（斜线、垂线、射影和平面内的直线）。
P O
A
a
α
定理内容阐述
2、“三垂线”的含义： 、 三垂线”的含义： （1）垂线与平面垂直 ） （2）射影与平面内的 ） 直线垂直 （3）斜线与平面内的 ） 直线垂直

三垂线定理及其逆定理 -回复

三垂线定理及其逆定理 -回复

三垂线定理及其逆定理 -回复
三垂线定理是指在一个三角形中，三条垂线的交点是三角形的垂心。

垂心是指三角形三条边上的高的交点。

三垂线定理表明，不论三角形的形状如何，垂心始终存在且唯一。

三垂线定理的逆定理是指如果在一个三角形中存在一个点，使得从该点到三条边上的垂线都相交于三角形的各边的中点，那么该点就是三角形的垂心。

简而言之，如果一个点满足垂线相交于各边中点的条件，那么该点就是三角形的垂心。

三垂线定理及其逆定理在三角形的几何证明和计算中具有重要的应用。

它们帮助我们确定垂心的位置，从而进一步推导出三角形的性质和关系。

三垂线定理

三垂线定理

O
a
α
A
三垂线定理
说明：
1、三垂线定理描述的是 三垂线定理 PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 P
A 2、a与PO可以相交，也可以异面。 α o a
3、三垂线定理的实质是平面的一条斜线和
江西省龙南中学 丁峤
平面内的一条直线垂直的判定定理。
三垂线定理
P A o
a
α
江西省龙南中学 丁峤
复习： 什么叫平面的斜线、垂线、射影？
三垂线定理
PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; AO
o
a
是PO在平面α内的射
影. 如果a α, a⊥AO， 思考a与PO的位置关 系如何？
α
三垂线定理
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
PA⊥α a α
PA⊥a ② a⊥平面PAO AO⊥a
P
a α
①
①
a⊥PO PO 平面PAO
③
A
o
②
③
线面垂直 性质
线线垂直
线面垂直 性质 判定定理
线线垂直
如果将定理“在 平面内”的条件去掉， 结论仍然成立吗？
例如：当 b⊥ 时， b⊥OA源自但 b不垂直于OPP
b
直线a 在一定要在平面 内，如果 a 不在平面内， 定理就不一定成立。

三垂线定理

三垂线定理

教师姓名学生姓名学管师学科数学年级上课时间月日：00--- ：00 课题三垂线定理及其逆定理教学目标三垂线定理及其逆定理的应用教学重难点三垂线定理在证明题中的各种应用教学过程知识点：1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用；【知识梳理】1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO分别是平面α的垂线和斜线，AO是PO在平面α的射影,,aα⊂a AO⊥。

求证：a PO⊥；证明：说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a与PO可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

aPOAα例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

PABC例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

例4.在正方体1AC 中，求证：11111,AC BD AC BC ⊥⊥； OCPBADD 1C 1B 1A 1DCBA2．写出三垂线定理的逆命题，并证明它的正确性； 命题： 已知： 求证： 证明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥； （2）点A 在底面BCD 上的射影是BCD ∆的垂心；例3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上 已知： 求证：aPOAαD A B C FE O αAC P B说明：可以作为定理来用。

例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3PAB PAc π∠=∠=。

三垂线定理

三垂线定理
PC=6，求点P到平面ABC的距离。 解: 作PH⊥平面ABC，
P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直 ∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内的射影 A
∴BC⊥AH
C H
B E
4×6 = ---12 在Rt△PBC中，PE= -----42+62 13 144 = ---2 29 在Rt△APE中，AE= PA2+PE2= 9+ --13 13
三垂线定理
例题分析：
1、判定下列命题是否正确 (1)若a是平面α 的斜线、直线b垂直于a在平面 α 内的射影，则a⊥b。 ( ×)
(2)若a是平面α 的斜线，b是平面α 内的直线， 且b垂直于a在β 内的射影，则a⊥b。 强调：1°四线是相对同一个平面而言 2°定理的关键找“平面”这个参照学。 ( ×)
PA⊥α a α
PA⊥a ② a⊥平面PAO AO⊥a
P
a α
①
①
a⊥PO PO 平面PAO
③
A
o
②
③
线线垂直 线线垂直 线面垂直 线面垂直 性质定理 判定定理 性质定理
三垂线定理
对三垂线定理的说明：
1、三垂线定理描述的是PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 2、a与PO可以相交，也可以异面。 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。
三垂线定理
小
结
三垂线定理：在平面内的一条直线，如果 和这个平面的一条斜线的射影垂直，那么它也 和这条斜线垂直。 1°定理中四条线均针对同一平面而言 2°应用定理关键是找“基准面”这个参照系 3°操作程序分三个步骤——“一垂二射三证”

三垂线定理及其逆定理

三垂线定理及其逆定理

三垂线定理及其逆定理令狐采学知识点： 1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用； 教学过程：1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直； 已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,,a α⊂a AO ⊥。

求证：a PO ⊥； 证明： 说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a 与PO 可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线P垂直的判定定理。

例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

例4.在正方体1AC 中，求证：11111,AC B D AC BC ⊥⊥； 2．写出三垂线定理的逆命题，并证明它的正确性；命题： 已知： 求证：证明： 说明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ∆的垂心； 例3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上 已知： 求证：说明：可以作为定理来用。

BDABC例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3PAB PAc π∠=∠=。

(1)求PA 与面ABC 所成的角的大小;(2)当PA 的长度等于多少的时候，点P 在平面ABC 内的射影恰好落在边BC 上； 作业：1.正方体1111D C B A ABCD -,,E F 分别是1,A A AB 上的点,1EC EF ⊥. 求证:1EF EB ⊥。

三垂线定理及逆定理

三垂线定理及逆定理

三垂线定理及逆定理三垂线定理是一个重要的几何定理，它掌握着许多几何形状的性质。

在这里，我们将介绍这个定理及其逆定理，并讨论它们在几何学中的应用。

三垂线定理：对于任意三角形ABC，它的边AB，AC通过C点的垂线BD，CD相交于点D。

那么，D点同时也在BC边上的垂线上。

这个定理的意思是，如果我们在三角形的两侧都有一条垂直线，它们都通过三角形的另一个点，在尖角处相交，那么这个交点也必须在三角形底边上的垂直线上。

这个定理可以用来进行几何证明，以及解决几何运算问题。

为了更好地理解这个定理，让我们看一看下面这张图。

![image.png](attachment:image.png)在这个三角形ABC中，我们可以看到点D是通过边AB和边AC的垂线相交而成的。

根据三垂线定理，D点也应该在BC边上的垂线上。

在图中，我们可以看到BC的垂线DE，它与AD相交于点F。

因此，根据三垂线定理，D点也应该在DE线上。

三垂线定理的逆定理是另一个重要的几何定理。

逆定理的意思是，如果我们能够证明一个点同时在三角形的底边上的垂线和其他两条垂直线上，我们就可以推断出这三条线相交于同一个点。

逆定理的表述如下：三垂线定理的逆定理：对于任意三角形ABC，如果BC的垂线DE与AD相交于点F，且DF和EF是三角形底边BC的垂线，则D、E、F三点共线。

这个逆定理与三垂线定理是完全相反的。

它表明，如果我们知道某个点在三条互相垂直的线上，则这些线都必须相交于同一个点。

这个定理可以帮助我们解决几何证明和运算问题。

总之，三垂线定理及其逆定理是几何学中重要的定理。

如果我们能够掌握它们的应用，就可以顺利解决许多三角形的几何问题。

无论是在学术上还是在生活中，这些定理都具有非常大的指导和应用价值。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三垂线定理
周口市第三高级中学 王杰
教学目标
三垂线定理是反映三种垂直关系的定理。

要求熟练掌握三垂线定理及逆定理，并据此
能够进行推理，论证和解决有关问题。

进一步提高学生利用数学知识解决实际问题的能力。

教学重难点
三垂线定理及其逆定理的理解和应用
教学方法
启发式教学法
依知识点的形成过程，实际问题的分析过程，启发学生寻求证明的途径，解决问题的
思路。

教学过程
引例：
如图，已知PA ⊥平面ABC ，∠ABC=90°，求证：BC ⊥PB 。

证明：∵PA ⊥平面ABC ，BC 在平面ABC 内， ∴PA ⊥BC ，又∠ABC=90°， ∴BC ⊥AB
∴BC ⊥平面PAB ，PB 在平面PAB 内 ∴BC ⊥PB
思考： （1）证明线线垂直的方法有哪些？
（2）三垂线定理及其逆定理的主要内容。

线线垂直的方法 ：
（1）a ⊥∂ ,b 在∂内，则a ⊥b
（2）a ∥b ，m ⊥b ，则a ⊥m
（3）三垂线定理及其逆定理
三垂线定理包含几种垂直关系？
○
1线面关系 ○2线射垂直 ○3线斜垂直 定理
直线和平面垂直 平面内的直线和平面 平面内的直线和平
的一条斜线射影垂直 面的一条斜线垂直
逆定理
三垂线定理： 在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，
它就和这条斜线垂直。

三垂线定理的逆定理： 在平面内的一条直线，如果和这个平面的一条斜线垂直，那
么，它也和这条斜线的射影垂直。

B
例1： 如图所示，已知PA ⊥平面ABC ，∠ACB= 90°， AQ ⊥PC ，AR ⊥PB ，试
证∆PBC 、 ∆PQR 为直角三角形。

证明：∵PA ⊥平面ABC ，∠ACB= 90°∴AC ⊥BC
∵AC 是斜线PC 在平面ABC 的射影 ∴BC ⊥PC
∴∆PBC 是直角三角形；∴BC ⊥平面PAC ∵AQ 在平面PAC 内，∴BC ⊥AQ ，又PC ⊥AQ ，
∴
AQ ⊥平面PBC ，∴QR 是AR 在平面PBC 的射影
又AR ⊥PB ，∴QR ⊥PB （三垂线逆定理），
∴∆PQR 是直角三角形。

小结： 凡是能够使用三垂线定理或逆定理证明的结论，都能由线面垂直的性质来证明，
而我们的目标应该是能够熟悉这两个定理的直接应用。

例2. 在四面体ABCD 中，已知AB ⊥CD
，AC ⊥BD 求证：AD 证明：作AO ⊥平面BCD 于点O ，连接BO ，CO ，DO
则BO ，CO ，DO 分别为AB ，AC ，AD 在平面BCD 上的射影。

∵AB ⊥CD ，∴BO ⊥CD ，同理CO ⊥BD 于是O 是△BCD 的垂心，
∴DO ⊥BC ，于是AD ⊥BC.
小结：运用三垂线定理及逆定理，必然要找出斜线，及作出该斜线在平面内的射影.
例3 . 如图，已知DB 、EC 都垂直于正三角ABC 所在的平面，，BC=EC=2DB ， 求平面ADE 与平面ABC 所成二面角的平面角。

解：延长ED 、BC 交于F ，连AF ，则AF 为二面角的棱
由已知DB 、EC 都垂直正三角ABC ，∴ DB//EC
又BC=EC=2DB ∴ FB=BC=AB ，∴ ∆FAC 为直角三角形，且FA ⊥AC 而EC ⊥平面ABC ∴ AF ⊥AE （三垂线定理） 于是∠EAC 为平面ABC 与平面ADE 的平面角，
又EC=AC ，∴ ∠EAC= 45° ∴ 二面角的平面角为45°。

思考：本题还可以用什么方法求二面角的平面角？
（ 用 c o s ABC ADE s S θ∆∆= ） 小结：求二面角往往是作出二面角的平面角，先确定二面角的棱，再设法过棱上一点在
二面角的两个半平面上作棱的两条垂线以找到平面角，从而转化为平面问题来解决。

作二面角的平面角常用的方法有（1）定义法（2）三垂线定理法（3）作垂面法。

此外射影面积定理也是求二面角大小的一种常用方法。

学习空间向量之后,我们还有另外的方法来求二面角,例如法向量法等.
例4： 直角三角形ABC 中，∠B= 90°，∠C= 30°，D 是BC 的中点，AC=2， DE ⊥平面ABC 且DE=1，求E 到斜线AC 的距离？ 解：过点D 作DF ⊥AC 于F ，连结EF ，
∵DE ⊥平面ABC ，由三垂线定理知EF ⊥AC
即E 到斜线AC 的距离为EF
在Rt ∆ABC 中， ∠B= 90°，∠C= 30°，C=2
A
∴
2CD ∴= ∵DF ⊥AC ，
∴4
CD = 在Rt ∆EDF 中
4EF =
为所求 小结：求点到直线的距离，常运用三垂线定理（或逆定理）把垂线段作出，按“一作、二证、三计算”的步骤求解。

方法规律 三垂线定理及其逆定理的应用：
（1）证明两条异面直线垂直；
（2）确定二面角的平面角；
（3）确定点到直线的垂线段。

运用定理时要习惯非常规位置图形上的应用，不能只习惯于水平放置的平面上运用。

能力拓展：
过Rt ∆BPC 的直角顶点P 作线段PA ⊥平面BPC ，求证： ∆ABC 的垂心H 是P 点在
平面ABC 内的射影。

证明：∵H 是∆ABC 的垂心，连结AH 延长交BC 于D
连结BH 延长交AC 于E ，∴AD ⊥BC ，BE ⊥AC
∵AP ⊥平面PBC ，∴BC ⊥PD ，AD ∩PD=D ∴BC ⊥平面ADP ，∴BC ⊥PH
又AP ⊥面PBC ，∴AP ⊥PB ，由已知BP ⊥PC ，∴PB ⊥面APC
又BE ⊥AC ，∴PE ⊥AC ，∴AC ⊥面PBE ，∴PH ⊥AC ∵AC ∩BC=C ，∴PH ⊥面ABC
∴H 是P 点在平面ABC 的射影。

练习：
1. (1) PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点 求证：PO ⊥BD ，PC ⊥BD
(2) PA ⊥平面PBC ，PB=PC ，M 是BC 的中点， 求证：BC ⊥AM
(3) 在正方体1AC 中，求证：1AC ⊥11B D ，1AC
⊥1BC 2. 证明：果一个角所在平面外一点到角的两边距离相等，那么这一点在平面上的射影在这个角的平分线上。

作业：
1. 在正方体1AC 中，E 、G 分别是1AA 和1CC 的中点， F 在AB 上，且1C E ⊥EF ， 则EF 与GD 所成的角的大小为（ ）
(A) 30° (B) 45° (C) 60° (D) 90°
2. 已知 PA 、PB 、PC 两两垂直，求证：P 在平面ABC 内的射影是△ABC 的垂心。

3. 经过一个角的顶点引这个角所在平面的斜线，如果斜线和这个角两边的夹角相等，那么 斜线在平面上的射影是这个角的平分线所在的直线。

4. 在ABCD —1111A B C D 中，求证：1AC ⊥平面1BC D
B。