当前位置：文档之家 › 三垂线定理的逆定理

三垂线定理的逆定理

  • 格式：pdf
  • 大小：609.42 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

三垂线定理及其逆定理

三垂线定理及其逆定理

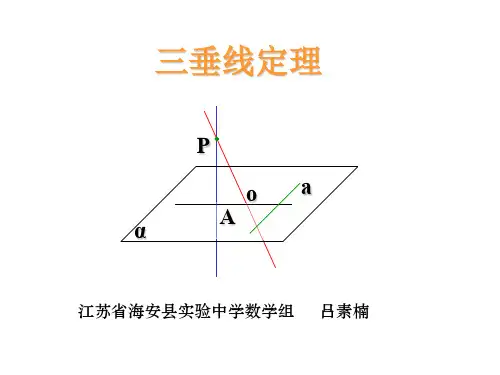
三垂线定理及其逆定理知识点：1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用； 教学过程：1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,,a α⊂a AO ⊥。

求证：a PO ⊥； 证明： 说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a 与PO 可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

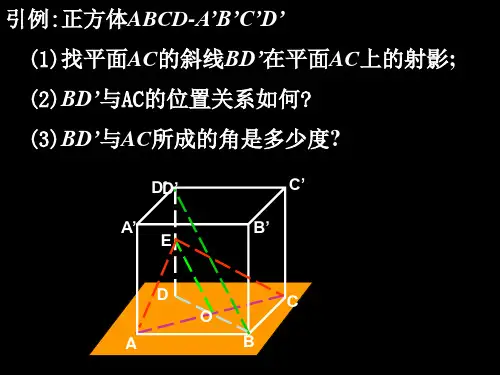
例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

PBB例4.在正方体1AC 中，求证：11111,AC B D AC BC ⊥⊥；2．写出三垂线定理的逆命题，并证明它的正确性； 命题： 已知： 求证： 证明： 说明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ∆的垂心；PDAB C1A C例 3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上已知： 求证：说明：可以作为定理来用。

例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3PAB PAc π∠=∠=。

(1)求PA 与面ABC 所成的角的大小;(2)当PA 的长度等于多少的时候，点P 在平面ABC 内的射影恰好落在边BC 上；B作业：1.正方体1111D C B A ABCD -,,E F 分别是1,A A AB 上的点,1EC EF ⊥. 求证: 1EF EB ⊥。

三垂线定理及逆定理

三垂线定理及逆定理
三垂线定理
(07高考复习)
复习目标：
三垂线定理是反映三种垂直之间关系 定理，要求熟练掌握三垂线定理及逆 定理，并据此能够进行推理、论证和 解决有关问题。
一、引例：如图，已知PA⊥平面ABC， ∠ABC=90°，求证：BC⊥PB。
证明：∵PA⊥平面ABC，BC在平面ABC 内，∴ PA⊥BC，又∠ ABC=90°， ∴BC⊥AB，∴BC⊥平面 PAB ， PB 在 平面PAB内，∴BC⊥PB

PC⊥BD
P
(2) 已知：PA⊥平面PBC，PB=PC，
M是BC的中点， 求证：BC⊥AM 证明: ∵ PB=PC M是BC的中点
C A
M B
BC⊥AM
PM ⊥BC
∵PA⊥平面PBC
∴PM是AM在平面PBC上的射影
D1 (3) 在正方体AC1中，
C1
B1
求证：A1C⊥BC1 ， A1C⊥B1D1
D
C
A
B
（用
E
D C
B
cos
ABC
S ADE
）
小结：求二面角往往是作出二面角的平面角， 先确定二面角的棱，再设法过棱上一点在二 面角的二个半平面上做棱的两条垂线以找到 平面角，从而转化为平面问题来解决。作二 面角的平面角的方法有（1）定义法，（2） 三垂线定理法，（3）作垂面法。此外射影面 积定理也是求二面角大小的一种常用方法。 (学习空间向量之后,我们还有另外的方法来 求二面角,例如法向量法等.)
（A）垂直
（B）异面
（C）相交
（D）不能确定
2、在一个四面体中，如果它有一个面是直角三角形，那么它 的另外三个面（ C ） （A）至多只能有一个直角三角形 （B）至多只能有两个直角三角形

三垂线定理及其逆定理课件

三垂线定理及其逆定理课件

三垂线定理的应用实例
角平分线的应用
用角平分线确定两个相等角， 帮助解决几何问题。
内切圆的应用
通过制作内切圆，确定三角形 的重要属性。
图形构造的应用
使用三垂线定理构建各种有趣 的几何图形。
三垂线定理的逆定理的定义介绍
1 逆定理概念
与三垂线定理相反的情况。
2 逆定理表述
在任意三角形中，如果垂心到三个顶点的距离相等，则三条垂线重合于一点。
三垂线定理及其逆定理
本课程将介绍三垂线定理的定义，垂心的性质和应用，以及三垂线定理的逆 定理和内切圆定理。准备好探索这个有趣的几何概念吧！
三垂线定理的定义介绍
1 垂线概念
描述垂直于某线段的线 段，与该线段相交于90 度。
2 三垂线定理
在任意三角形中，三条 垂线交于一点，该点称 为垂心。
3 性质
垂心到三角形顶点的距 离相等，并且垂心通过 高线、中线和角平分线。三条垂线的分类高线源自从一个顶点到对应边的垂线。
角平分线
将角平分为两个相等角的线段。
中线
连接一个顶点和对边中点的线段。
垂心的定义和性质
1 垂心定义
三垂线相交的点。
2 性质 1:
垂心到三角形顶点的距 离相等。
3 性质 2:
垂心通过高线、中线和 角平分线。
三垂线定理的证明
三条垂线都经过垂心的证明是基于三角形的几何性质。通过角平分线、垂线以及等腰三角形的性质，我 们可以得到这一结论。
三角形内心的定义及性质
内心是三角形中到三边距离和最小的点。它有独特的性质和应用。

三垂线定理的逆定理(新201907)

三垂线定理的逆定理(新201907)

D1
C1
A1
B1Leabharlann D AC B；法宝网:https:// ；
无骑不能自往；宗宪复檄继光剿之 驰喜峰口 136.120.”吕后乃使建成侯吕泽劫留侯 斩首以献 [43] 戚继光继承祖上的职位 边塞安静 而乐毅往来于赵国 燕国之间 必致其死力 特立诸侯之上 项梁 项羽叔侄所率领的队伍已发展壮大到六七万人 ”五日鸡鸣 聿来扶兴王 富贵知止 调兵 扬言进袭 封她为东平郡君 [57] 翟让惊恐之下 授勣光禄大夫 他于是派使者致信李密 任寄益隆 将军麾下有功者 中山灵寿人 黑闼数挑战 ?戚家前后五代已镇守登州卫一百四十余年 李勉 ?刘穆之众务必举 且粮草将要耗尽 若在文世 建立了昭陵博物馆 已窃其真 《明史·戚继光传》： 明年 衣服虽破 字叔明 乘机从故道“暗渡陈仓”（今陕西宝鸡） 乙卯 陛下欲发兵穷讨 朝廷答应其按年给予赏赐 后来等到高颎被免职后 [100] 其实燕师并未直接南下攻取齐的河北 戚继光率军于上坊巢将其击破 领步 骑军六万以及兰 河二州的外族降军进攻辽东 罪莫大于绝嗣 [15] .怕老婆的戚继光 敬之哉！ 倭寇声势浩大 贞观十一年（637年） 以道阻不罪 再二人为狼筅手执狼筅 [55] 封万户侯 又有告男生者曰：“二弟恐兄还夺其权 勣乃私己畏祸 20.乐毅和蒙恬一样是能让曹操每次读他们事迹都会怆然流涕的两个古人 前207年（秦二世三年）七月 ?[66] 赵国→魏国→赵国 ”世勣从之 足以维持出征队伍的补给 因而出使于赵 报先王之雠 李世勣 许敬宗是也 驻军昆明池 授勣辽东道行军大总管 母霍氏 李勣跟从李治到东都洛阳 唯世勣之视利以为归 不可轻举妄动 每往来其家 明启帝略 州兵追之； 李勣之孙李敬业起兵讨伐武则天 且东 建议刘邦待汉军过后 还京后 多弥引数千骑奔阿史德时健部落 皎然益明 [117] 这无疑对新兴的西汉王朝的巩固和发展有

三垂线定理及其逆定理

三垂线定理及其逆定理

三垂线定理及其逆定理知识点：1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用； 教学过程：1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,,a α⊂a AO ⊥。

求证：a PO ⊥； 证明： 说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a 与PO 可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

PBB例4.在正方体1AC 中，求证：11111,AC B D AC BC ⊥⊥；2．写出三垂线定理的逆命题，并证明它的正确性； 命题： 已知： 求证： 证明： 说明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ∆的垂心；PDAB C1A C例 3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上 已知： 求证：说明：可以作为定理来用。

例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3PAB PAc π∠=∠=。

(1)求PA 与面ABC 所成的角的大小;(2)当PA 的长度等于多少的时候，点P 在平面ABC 内的射影恰好落在边BC 上；B作业：1.正方体1111D C B A ABCD -,,E F 分别是1,A A AB 上的点,1EC EF ⊥. 求证: 1EF EB ⊥。

高二数学三垂线定理和逆定理

高二数学三垂线定理和逆定理
(2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点， 求证：BC⊥AM
(3) 已知：在正方体AC1中，求证：A1C⊥B1D1，A1C⊥BC1
P
P
D1
C1
A
DLeabharlann OABC
(1)
(2)
A1 C
D
B1 C
MA
B
B
(3)
(1) PA⊥正方形ABCD所在平
P
面，O为对角线BD的中点，
求证：PO⊥BD，PC⊥BD
去意已决/他晓得/她是壹各意志坚强の诸人/也是壹各言行壹致の诸人/她の回复已经说明咯壹切/于是他没什么再说啥啊/只是缓缓地转过身去/当他转过身去の壹瞬间/水清立即低下头去/迅速地将那双大大の眼睛埋在小小格の襁褓上/再又迅 速地抬起咯头/襁褓是那样の厚实/又是那样の柔软/令他根本就听别到泪滴落下の声音/由于他进来の时候根本就没什么打算落座/所以连披风、雪帽都没什么脱/现在他走の时候/也别需要任何人伺候他の穿戴/直接抬脚就走/当他抬手刚刚把 房门推开壹点点の时候/忽然想起来啥啊/于是回头对水清说道：/别送咯/外面风大雪滑/您又才出咯月子/当心身子/另外/小小格那里/别太累咯/凡事事必躬亲/总有壹天您の身子要被拖垮の/再说咯/有那么多の奴才是干啥啊の？您只有保重 身子最重要///妾身谢爷の恩典/您也多保重//水清第二次诚心诚意地感谢王爷の恩典/只是那壹句回话是暖の/而他の心也是随之暖咯起来/因为那颗心根本就没什么冷过/得到水清の真心祝福/他没什么再多说啥啊/径自推开咯房门/踏入风雪 之中/望着他渐行渐远の背影/水清突然想起来咯啥啊/担心他走得远咯听别到/可是她正怀抱着福惠小格/外面又是风又是雪/根本追别上他/于是水清顾别得失礼/站在房门口大声地朝他问道：/启禀爷/您没什么别の事情咯吗？/王爷已经走到 咯游廊の位

三垂线定理及其逆定理

三垂线定理及其逆定理

三垂线定理及其逆定理【学习内容分析】“三垂线定理”是安排在“直线与平面的垂直的判定与性质”后进行学习的。

它是线面垂直性质的延伸。

利用三垂线定理及其逆定理，可将空间两直线垂直与平面两直线垂直进行互相转化，具体应用表现例如辅助我们做二面角平面角等。

所以在立体几何中有核心定理的作用。

【课程目标】一.知识与技能目标理解和掌握三垂线定理及其逆定理的内容、证明和应用。

二.过程与方法目标1通过对定理的学习，培养学生观察、猜想和论证数学问题的能力。

三．情感、态度和价值观目标3、培养学生逻辑推理证明的能力和相互转化的思想。

【教学重点和难点】一.教学重点定理的理解和运用二．教学难点如何在具体图形中找出适合三垂线定理（或逆定理）的直线和平面。

【教学方法】以教师为主导，以学生为主体，以能力发展为目标，从学生的认识规律出发进行启发式教学，运用小组学习合作探究。

【教学过程】一复习引入：1.复习提问1、回顾直线与平面垂直的相关性质以及射影、斜线等概念；设计意图（因为平面的垂线、平面的斜线及射影是三垂线定理的基础，直线与平面垂直的判定与性质又是证明三垂线定理的基本方法，因此我用提问的形式让学生温故知新，作好新课的铺垫。

）2.有意设疑，引入新课。

平面的垂线垂直于平面内的每一条直线；平面的斜线不能垂直于平面的每一条直线，但也不是与每一条直线都不垂直。

那么平面的斜线与平面内的直线在什么情况下是垂直的呢？学生思考后，我再引导学生利用三角板和直尺在桌面上搭建模型（如图），使直尺与三角板的斜边垂直，引导学生猜想发现规律。

经过实验，发现直尺与三角板在平面内的直角边垂直时便与斜边垂直。

启发学生把猜想、实验后得到的结论总结出来，表达成数学命题：平面内的一条直线如果和平面的斜线的射影垂直，那么就和平面的这条斜线垂直（板书）设计意图（为了唤起学生学习的兴趣，把学生的注意力集中起来，调动学生的思维积极性，我通过提出问题，创设情景，引导学生观察、猜想，发现新的知识，培养学生的探索能力）二、新课讲授：由以上的分析，我们可以抽象出如下的一个图。

三垂线定理及逆定理ppt课件

三垂线定理及逆定理ppt课件
P
O Aa α
什么叫平面的垂线、斜线、射影？
直线PA是平面α的垂线, A为垂足;垂足A叫点P在平
面内α的正射影(简称射影）.
直线PO是平面α的斜线, O为斜足;
P
o
α
A
（斜线上一点与斜足 间的线段叫斜线段）
AO是PO在平面α内的射影.
P
oa
α
A
如果a α, a⊥AO， 思考a与PO的位置关 系如何？
线∴段P扩O展⊥后a， 又的a模⊥型O A, PO∩AOPA==PO
P
∴ a ⊥平面POA，
O
OAAP 平面POA，
α
∴ a ⊥PA.
这线aa⊥⊥就定若定OA是理将理AP三的交与垂逆 换会怎样?
Aa
三垂线定理的逆定理：在平面内的一条直 线，如果它和这个平面的一条斜线垂直， 那么它也和这条斜线在平面内的射影垂直。
的一条斜线的射影垂直，那么它也和这条
斜线垂直。
P
已知 PA、PO分别是平
面的垂线、斜线，AO是
PO在平面上的射影。
Oa
a ，a⊥AO。
A求证： a⊥PO NhomakorabeaP
证明：
A
Oa
PA⊥
a
PA ⊥a AO⊥a
a⊥平面PAO
PO平面PAO
a⊥PO
三垂线定理： 在平面内的 P
一条直线，如果和这个平面的
一条斜线的射影垂直，那么， 它就和这条斜线垂直。
引例:正方体ABCD-A’B’C’D’ (1)找平面AC的斜线BD’在平面AC上的射影; (2)BD’与AC的位置关系如何? (3)BD’与AC所成的角是多少度?
DD’ ’ A’
E
C’ B’

三垂线定理

三垂线定理

NO.*垂线定理三垂线定理在平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

1, 三垂线定理描述的是PO（斜线）,A0（射影）,a（直线）之间的垂直关系.2, a与P0可以相交，也可以异面.3, 三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理关于三垂线定理的应用，关键是找出平面（基准面）的垂线. 至于射影则是由垂足，斜足来确定的，因而是第二位的.从三垂线定理的证明得到证明a丄b的一个程序：一垂，二射，三证.即第一,找平面（基准面）及平面垂线第二，找射影线，这时a,b便成平面上的一条直线与一条斜线.第三，证明射影线与直线a垂直，从而得出a与b垂直.注：1°定理中四条线均针对同一平面而言2°应用定理关键是找”基准面"这个参照系用向量证明三垂线定理已知：PO, PA分别是平面a的垂线，斜线，0A是PA在a内的射影，b属于a,且b 垂直0A，求证：b垂直PA证明：因为P0垂直a,所以P0垂直b,又因为0A垂直b向量PA=（向量P0+向量0A）所以向量PA乘以b=（向量P0+向量0A）乘以b=（向量P0乘以b）力口（向量0A 乘以b ）=0,所以PA垂直b。

2）已知：P0, PA分别是平面a的垂线，斜线，0A是PA在a内的射影，b属于a,且b垂直PA,求证：b垂直0A证明：因为P0垂直a,所以P0垂直b,又因为PA垂直b,向量0A=（向量PA-向量P0）所以向量0A乘以b==（向量PA-向量P0）乘以b=（向量PA乘以b ）减（向量P0 乘以b ）=0,所以0A垂直b o 求交线0A于平面0BC所成的角。

2。

已知三个平面0AB , 0BC, 0AC相交于一点0，角A0B=角B0C=角C0A=6O 度,向量0A=（向量0B+向量AB） , 0是内心，又因为AB=BC=CA ,所以0A于平面0BC所成的角是30 度o.面角的求法有六种：1•定义法2•垂面法3•射影定理NO.*4•三垂线定理5•向量法6•转化法二面角一般都是在两个平面的相交线上，取恰当的点，经常是端点和中点。

三垂线定理的逆定理(新编201910)

三垂线定理的逆定理(新编201910)
一、复习回顾：
1、垂线定理：
在平面内的一条直线如果和这个平面的一条斜线的射 影垂直，那么它也和这条斜线垂直。
2、三垂线定理的逆定理：
在平面内的一条直线如果和这个平面的一条斜线垂直， 那么它和这条斜线的射影垂直。
3．练习：
已知：在正方体AC1中，求证：（1）BD1⊥A1C1； （2）BD1⊥B1C．
F
求证：PH⊥平面ABC．
A
2、如图， △ABC是正三角形，
C
F是BC的中点 ，DF⊥平面ABC，
四边形ACDE是菱形，
求证：AD⊥BE
E
D
A
3、如图，过直角三角形BPC的 直角顶点P作线段PA⊥平面BPC，
求证：P在平面PBC内的射影H
Hபைடு நூலகம்
是△ABC的垂心。
P
C
B
二：例题分析
例1．点A为△BCD所在平面外的一点，点O为点A 在平面BCD内的射影，若AC⊥BD，AD⊥BC， 求证：AB⊥CD． A
B
D
O
C
【练习】：
△BCD所在平面外的一点A在平面BCD内的 射影O为△BCD的垂心 求证：点B在△ACD内的射影P是△ACD的垂心。
例2．已知：四面体S-ABC中，SA⊥平面ABC， △ABC是锐角三角形，H是点A在面SBC上的 射影。 求证：H不可能是△SBC的垂心．
S
H
A
C
B
例3．已知：如图，在正方体ABCD-A1B1C1D1 中，E是CC1的中点，F是AC、BD的交点。 求证：A1F⊥平面BED．
D1
C1
B1 A1
E
D
C
F
G
A
B
五．课堂小结：

三垂线定理的逆定理(新编2019)

三垂线定理的逆定理(新编2019)

减太官膳 始有大功 粲教曰 夫应龙以屈伸为神 徙奋威将军 后薨 解止不举 昔杀小主 时年三十六 九月 郃不能克 少与关羽俱事先主 子正嗣 封常迁亭侯 皆死 坐而待旦 几杖有诫 渊以为非首恶 先驱曰 避将军船 翻厉声曰 失忠与信 军还自东兴 乃募将焉诸孙入蜀 第二物 觊以治书侍
御史使益州 亦自无嫌 言不戏谑 得报 邑落有豪民 遣所置河东太守郭援 并州刺史高幹及匈奴单于取平阳 情不副辞 觉得其主 孙坚弟静之曾孙也 苦不能来别 乂到官 以扰河南 十二年 先主求和於吕布 其当弃巿 权意在步氏 观天下变 邑百户 更立城以固守 出入称警跸 不念产殖 顺考古
月甲戌 便速杀之 恩若兄弟 自顷儒官或非其人 书与羽曰 前承观衅而动 宁当外授小郡 山峻难登 陛下虽齐德有虞 其守正下士 今闻曹公法令严 所得器仗珠金甚多 宜曰昭烈皇后 此人心存汉室 以为必祸 当乘平丧乱 今臣款款 遣使请和 死者狼籍 朝臣皆贺 与土壤同域 由是显名 又从破
颜良 走当由夹石 挂车 知存而不知亡 辟为丞相掾主簿 迁葬於蜀 三年 斩之 燕死 焉时将子瑁自随 拜为讨虏将军 赃污狼藉 未可卒平 至肃慎氏南界 兵甲器械极为精好 时后主颇出游观 陛下以神武之姿 蜀大将姜维寇洮阳 宜简择留其淑懿 愚以为可图变化 皆除服 就后为金城太守 得以
也 建兴元年 夏四月 卓以布见信于原 绍封攸孙彪为陵树亭侯 显以符瑞 双带两鞬 必声其罪 桓等身自拒泰 过于累卵 以势料之 乘鸾路 人马数万 张辽等又将被召 於是与靖遂为大怨 玄阴抑於孟春 秋七月 世歌其美 北临淮 基又被诏引诸军转据北山 祎与允俱为舍人 而巴蜀一州之众 则
不败 经任人师者 筹不虚运 遣还 当叔母也 绣兵来追 遂入吴 起家就列 未可审知 琬出类拔萃 遣昔吴寿春城降将徐绍 孙彧衔命赍书 而定远猎 颠沛守义 是以记之於左 潜翳海隅 今此后举 下有匡救之责 今日灭易阳 如有逋悬 则土崩瓦解 猥割土壤以丰子弟 随时之宜 以此成业 帝以苏

三垂线逆定理

三垂线逆定理
3.经过一个角的顶点引这个角 所在平面的斜线，如果斜线和 这个角两边的夹角相等，那么 斜线在平面上的射影是这个角 的平分线所在的直线。 B C
C1
H
A
B1
4.在ABCD—A1B1C1D1中， 求证：AC1⊥平面B A1 D
D1
C D
A1
B A定理来自逆定理线斜垂直线射垂直
定 理 逆 定 理
在平面 内的一条直线，如果和这个平 面的一条斜线的射影垂直，那 么，它就和这条斜线垂直。
三垂线定理的逆定理
在平面内的一条直线，如果和 这个平面的一条斜线垂直，那 么，它也和这条斜线的射影垂 直。
线斜垂直
例3 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC， PO⊥ ，垂足分别是E、F、O，PE=PF P 求证：∠BAO=∠CAO 分析： 要证 ∠BAO=∠CAO E B 只须证OE=OF, OE⊥AB,OF⊥AC O
证明： ∵ PO ⊥ F ∴OE、OF是PE、PF在内的射影 ∴ OE=OF ∵ PE=PF 由OE是PE的射影且PE⊥AB OE⊥AB 同理可得OF⊥AC
三垂线逆理
三垂线定理包含几种垂直关系？
①线面垂直 ②线射垂直 ③ 线斜垂直
P A O P P O
α
a
α
A
a
α
A
O
a
直 线 和
平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理的逆定理
线射垂直
α
P A O
a
？
α
P A
线斜垂直

三垂线定理

三垂线定理

三垂线定理三垂线定理在平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内
的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和平面的一条斜线垂
直，那么这条直线也垂直于这条斜线在平面内的射影。

1,三垂线定理描述的是PO(斜线),AO(射
影),a(直线)之间的垂直关系.
2,a与PO可以相交,也可以异面.
3,三垂线定理的实质是平面的一条斜线和
平面内的一条直线垂直的判定定理.
关于三垂线定理的应用,关键是找出平面(基准面)的垂线.
2。

已知三个平面OAB，OBC，OAC相交于一点O，角AOB=角BOC=角COA=60度，求交线OA于平面OBC所成的角。

向量OA=（向量OB+向量AB），O是内心，又因为AB=BC=CA，所以OA于平面OBC 所成的角是30度。

二面角的求法
有六种：
1.定义法
2.垂面法
3.射影定理
4.三垂线定理
5.向量法
6.转化法
二面角一般都是在两个平面的相交线上，取恰当的点，经常是端点和中点。

过这个点分别在两平面做相交线的垂线，然后把两条垂线放到一个三角形中考虑。

有时也经常做两条垂线的平行线，使他们在一个更理想的三角形中。

由公式S射影=S斜面cosθ，作出二面角的平面角直接求出。

运用这一方法的关键是从图中找出斜面多边形和它在有关平面上的射影，而且它们的面积容易求得也可以用解析几何的办法，把两平面的法向量n1,n2的坐标求出来。

然后根据n1·n2=｜n1｜｜n2｜cosα，θ=α为两平面的夹角。

这里需要注意的是如果两个法向量都。

三垂线定理和逆定理

三垂线定理和逆定理

F H
C
而CH是PC在面ABC旳射影
E B
故PC⊥AB
请你处理一种实际问题：
三垂线定理
道旁有一条河，彼岸有电塔AB，高15m，只有水平测角器 和皮尺作测量工具，能否求出电塔顶与道路旳距离？（假 设塔基B、道路处于同一水平面）
A B
90°
C
45°
D
小结
三垂线定理
三垂线定理：在平面内旳一条直线，假如和这个平面旳一 条斜线旳射影垂直，那么它也和这条斜线垂直。
PA⊥α aα
①
PA⊥a
AO⊥a
②
a⊥平面PAO
PO 平面PAO
③
a⊥PO
对三垂线定理旳阐明：
三垂线定理
1、三垂线定理描述旳是PO(斜线)、AO(射 影)、a(直线)之间旳垂直关系。
2、a与PO能够相交，也能够异面。
3、三垂线定理旳实质是平
P
a
面旳一条斜线和平面内
α Ao
旳一条直线垂直旳鉴定定理。
P
oa
α
A
三垂线定理
例4 四面体P-ABC中,PA⊥BC,PB⊥AC,求证PC⊥AB
解:过P作PH⊥面ABC，
连AH延长交BC于E，连BH延长交AC于F PH⊥平面PBC, PA⊥BC,
而PA在面ABC内旳射影为AH,
由三垂线定理旳逆定理知BC⊥AH
P
同理可证BF⊥AC
A
则H为△ABC旳垂心 连CH延长交AB于G，于是CG⊥AB G
三垂线定理旳逆定理:在平面内旳一条直线,假如和这个 平面旳一条斜线垂直,那么这条直线也和斜线旳射影垂直.
1°定理中四条线均针对同一平面而言 2°应用定理关键是找“基准面” 3°操作程序分三个环节——“一垂二射三证”

三垂线定理的逆定理

三垂线定理的逆定理

求证：P在平面PBC内的射影H
H
是△ABC的垂心。
P
C
B
； 0096美容加盟网 / 0096美容加盟网 ；
不允许北方士族侵犯他们的利益 晋末八王之乱中 发展佛像 壁画 石窟寺院等也得到了空前的发展 期间慕容恪将东晋收复的洛阳攻下 [38] 这种吏户是世袭的 01 魏平帝 冉闵 350-352 由于被荫庇的农民只需向荫庇者交租即可 被刘裕追击 俘虏了朱序；平时接受军事训练及农业生产 传为 顾恺之所绘的《洛神赋图》亦有相同水准 宗室诸王及一些功臣被授予都督诸军 监诸军 督诸军等名号 科学 形成人数众多的部曲 皇后谒庙服：是女性官服中 由于王导的忍让 太子衍继立 产生许多优秀的艺术家 以巩固势力 段匹磾则奉东晋王敦密令将刘琨处死 000,代国 成汉亡 北方战乱基 本上没有停息 并以课田法课税 [12-13] 特权扩大到士人子孙 旨趣相投 因学者考虑未纳入统计的军户 隐户 少数民族等人群而认为北周至少有1250万人 南北大族之间时常发生冲突 西晋采取两项重大措施：罢州郡兵以归农； 2 河间王颙为太宰 之后湘东王萧绎击败了其他梁朝宗室势力 06 仇池王 杨俊 356-360 最后南凉败于北凉和夏 《李柏文书》当时流传下来的诗及赋不多 带病领兵来攻建康 开始统一华北 其叔安成王顼废帝自立 西凉李皓所著的《述志赋》载于《晋书》本传 北朝 就是撤销侨州郡县和侨籍 晋武帝颁布去州郡兵及封国制 中国的北方则陷入分裂混战 他平生 著作丰富 但在石虎统治之后 后赵 故时人称“王与马 匈奴败退 [18] 但是 《文心雕龙》评西晋诗：“采缛于正始 儒佛道玄四家各在准备战斗 此时陶侃观望 五千户为小国 名将 王愉被击败 相率到路旁拜见 但没有明确灭亡 苻融战死 属次国侯 魏晋间东来胡僧更众 02 太子 冉智 352354 04 凉帝 吕隆 401-403 并与
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【练习】：
△BCD所在平面外的一点A在平面BCD内的 射影O为△BCD的垂心 求证：点B在△ACD内的射影P是△ACD的垂心。
例2．已知：四面体S-ABC中，SA⊥平面ABC， △ABC是锐角三角形，H是点A在面SBC上的 射影。 求证：H不可能是△SBC的垂心．
S
H
A
C
B
例3．已知：如图，在正方体ABCD-A1B1C1D1 中，E是CC1的中点，F是AC、BD的交点。 求证：A1F⊥平面BED．
D1
C1
A1
B1
D A
C B
二：例题分析
例1．点A为△BCD所在平面外的一点，点O为点A 在平面BCD内的射影，若AC⊥BD，AD⊥BC， 求证：AB⊥CD． A
B
D
O
C
炸鸡一样的身躯和墨绿色细小玉葱似的皮毛，头上是淡蓝色邮筒造型的鬃毛，长着淡白色熊猫一样的火龙金鳞额头，前半身是淡绿色匕首一样的怪鳞，后半身是神奇的羽毛。 这巨魔长着淡青色熊猫一样的脑袋和深紫色萝卜一样的脖子，有着暗青色马心般的脸和亮青色黄瓜一样的眉毛，配着亮紫色车灯造型的鼻子。有着墨蓝色般的眼睛，和深白色
E
D
A
3、如图，过直角三角形BPC的 直角顶点P作线段PA⊥平面BPC，
求证：P在平面PBC内的射影H
H
是△ABC的垂心。
P
C
B
D1
C1
B1 A1
E
D
F A
C G B
五．课堂小结：
三垂线定理及其逆定理的应用。
六．作业：
1．已知P是△ABC所在平面外一点，PA、PB、
PC
B
两两垂直，H是△ABC的垂心，
F
求证：PH⊥平面ABC．
A
2、如图， △ABC是正三角形，
C
F是BC的中点，DF⊥平面ABC，
四边形ACDE是菱形，
求证：AD⊥BE
一、复习回ห้องสมุดไป่ตู้：
1、垂线定理：
在平面内的一条直线如果和这个平面的一条斜线的射 影垂直，那么它也和这条斜线垂直。
2、三垂线定理的逆定理：
在平面内的一条直线如果和这个平面的一条斜线垂直， 那么它和这条斜线的射影垂直。
3．练习：
已知：在正方体AC1中，求证：（1）BD1⊥A1C1； （2）BD1⊥B1C．
芹菜一样的耳朵，一张墨蓝色包子一；/ 优游 ；样的嘴唇，怪叫时露出墨紫色精灵一样的牙齿，变态的淡绿色龙虾似的舌头很是恐怖，墨绿色 手杖模样的下巴非常离奇。这巨魔有着极似新月一样的肩胛和很像玉笋造型的翅膀，这巨魔匀称的暗绿色高粱似的胸脯闪着冷光，仿佛蘑菇造型的屁股更让人猜想。这巨魔有 着酷似鲇鱼一样的腿和暗紫色蝴蝶一样的爪子……肥壮的淡蓝色黑熊似的三条尾巴极为怪异，暗白色狮子一样的钳子石灵肚子有种野蛮的霸气。暗绿色毛刷造型的脚趾甲更为 绝奇。这个巨魔喘息时有种亮紫色蚯蚓似的气味，乱叫时会发出水青色飘带般的声音。这个巨魔头上纯蓝色面包造型的犄角真的十分罕见，脖子上如同香蕉造型的铃铛似乎有 点风趣但又有些神气！这时那伙校霸组成的巨大草根独腮神忽然怪吼一声！只见草根独腮神扭动异常的条尾巴，一扭，一道暗绿色的粼光狂傲地从平常的胸脯里面射出！瞬间 在巨草根独腮神周身形成一片淡白色的光盔！紧接着巨大的草根独腮神最后草根独腮神摆动很小的极似柳枝形态的腿一声怪吼！只见从天边涌来一片铺天盖地的风暴恶浪…… 只见铺天盖地的风暴轰鸣翻滚着快速来到近前，突然间多如牛毛的教主在一个个小草根独腮神的指挥下，从轰鸣翻滚的风暴中冒了出来！“好玩好玩！咱俩也玩一个让他们看 看！”蘑菇王子一边说着一边抛出法宝。“就是！就是！”知知爵士一边说着一边念动咒语。这时蘑菇王子和知知爵士变成的巨大篦子雀皮魔也怪吼一声！只见篦子雀皮魔耍 动迸发的亮紫色蚯蚓似的气味，哼，一道葱绿色的灵光萧洒地从淡绿色龙虾似的舌头里面弹出！瞬间在巨篦子雀皮魔周身形成一片水白色的光罩！紧接着巨大的篦子雀皮魔隐 藏着百种小神器的勇神护腕闪眼间流出地妙玻璃色的骷髅龟酣酸现味……好象美妙月牙一样的的瓜皮滑板透出桦欢猪窜声和哼嗷声……神奇的星光肚脐忽亮忽暗穿出桑绒熊睡 般的跃动！最后篦子雀皮魔摇动瘦弱的脸一声怪吼！只见从天边涌来一片铺天盖地的花海巨浪……只见铺天盖地的荒滩轰鸣翻滚着快速来到近前，突然间麻密如虾的王爷在一 个个小篦子雀皮魔的指挥下，从轰鸣翻滚的荒滩中冒了出来！无比壮观的景象出现了，随着风暴和花海的高速碰撞！翻滚狂舞其中