三垂线定理及其逆定理

三垂线定理及逆定理三垂线定理是一个重要的几何定理，它掌握着许多几何形状的性质。

在这里，我们将介绍这个定理及其逆定理，并讨论它们在几何学中的应用。

三垂线定理：对于任意三角形ABC，它的边AB，AC通过C点的垂线BD，CD相交于点D。

那么，D点同时也在BC边上的垂线上。

这个定理的意思是，如果我们在三角形的两侧都有一条垂直线，它们都通过三角形的另一个点，在尖角处相交，那么这个交点也必须在三角形底边上的垂直线上。

这个定理可以用来进行几何证明，以及解决几何运算问题。

为了更好地理解这个定理，让我们看一看下面这张图。

在这个三角形ABC中，我们可以看到点D是通过边AB和边AC的垂线相交而成的。

根据三垂线定理，D点也应该在BC边上的垂线上。

在图中，我们可以看到BC的垂线DE，它与AD相交于点F。

因此，根据三垂线定理，D点也应该在DE线上。

三垂线定理的逆定理是另一个重要的几何定理。

逆定理的意思是，如果我们能够证明一个点同时在三角形的底边上的垂线和其他两条垂直线上，我们就可以推断出这三条线相交于同一个点。

逆定理的表述如下：三垂线定理的逆定理：对于任意三角形ABC，如果BC的垂线DE与AD相交于点F，且DF和EF是三角形底边BC的垂线，则D、E、F三点共线。

这个逆定理与三垂线定理是完全相反的。

它表明，如果我们知道某个点在三条互相垂直的线上，则这些线都必须相交于同一个点。

这个定理可以帮助我们解决几何证明和运算问题。

总之，三垂线定理及其逆定理是几何学中重要的定理。

如果我们能够掌握它们的应用，就可以顺利解决许多三角形的几何问题。

无论是在学术上还是在生活中，这些定理都具有非常大的指导和应用价值。

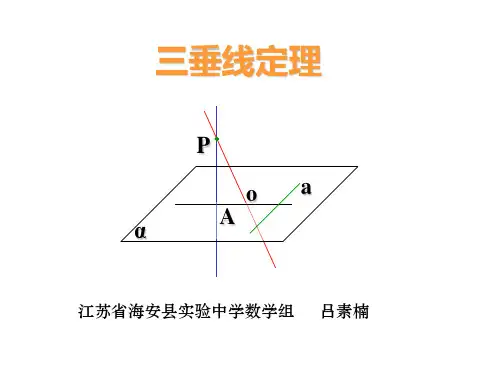
三垂线定理及其逆定理知识点：1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用； 教学过程：1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,,a α⊂a AO ⊥。

求证：a PO ⊥； 证明： 说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a 与PO 可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

PBB例4.在正方体1AC 中，求证：11111,AC B D AC BC ⊥⊥；2．写出三垂线定理的逆命题，并证明它的正确性； 命题： 已知： 求证： 证明： 说明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ∆的垂心；PDAB C1A C例 3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上已知： 求证：说明：可以作为定理来用。

例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3PAB PAc π∠=∠=。

(1)求PA 与面ABC 所成的角的大小;(2)当PA 的长度等于多少的时候，点P 在平面ABC 内的射影恰好落在边BC 上；B作业：1.正方体1111D C B A ABCD -,,E F 分别是1,A A AB 上的点,1EC EF ⊥. 求证: 1EF EB ⊥。

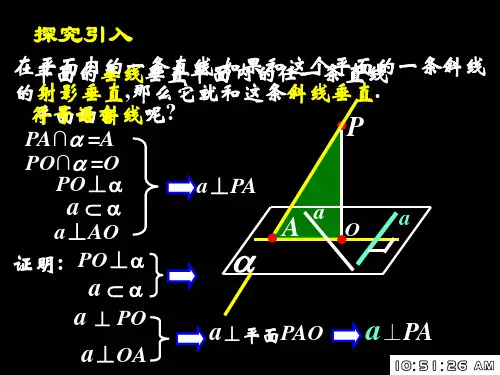
三垂线定理及其逆定理知识点：1.三垂线定理；；2.三垂线定理逆定理；3.综合应用； 教学过程：1．三垂线定理：平面内一条直线，如果和这个平面一条斜线在平面内射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO 分别是平面α垂线和斜线，AO 是PO 在平面α射影,,a α⊂a AO ⊥。

求证：a PO ⊥； 证明： 说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直方法：定义法；线线垂直判定定理；三垂线定理； （3）三垂线定理描述是PO(斜线)、AO(射影)、a(直线)之间垂直关系。

（4）直线a 及PO 可以相交，也可以异面。

（5）三垂线定理实质是平面一条斜线和平面内一条直线垂直判定定理。

例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 中点。

求证：,PO BD PC BD ⊥⊥。

PBB例4.在正方体1AC 中，求证：11111,AC B D AC BC ⊥⊥；2．写出三垂线定理逆命题，并证明它正确性； 命题： 已知： 求证： 证明： 说明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上射影是BCD ∆垂心；PDAB C1A C例 3.求证:如果一个角所在平面外一点到角两边距离相等，那么这点在平面内射影在这个角平分线上 已知： 求证：说明：可以作为定理来用。

例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 斜线，。

(1)求PA 及面ABC 所成角大小;(2)当PA 长度等于多少时候，点P 在平面ABC 内射影恰好落在边BC 上；B作业：1.正方体1111D C B A ABCD -,,E F 分别是1,A A AB 上点,1EC EF ⊥. 求证: 1EF EB ⊥。

三垂线定理及其逆定理
三垂线定理及其逆定理是数学中重要的定理，最早由18世纪欧洲数学家陶乐熙提出，也叫"数规"。

其定义是：
设有三角形的三个顶点A、B、C，则
1）如果两边上的顶点之间的垂直距离大于或等于这两边对应的边距离的总和，则称
为三垂线定理；
三垂线定理的图形表示如下：
在有限的三角形ABC中，设AD垂直平分BC边，则有：
AC + AD >= AB 。

显然，当有AD = AB/2时，即可满足“AC + AD >= AB”，称为三垂线定理。

类似地，当有AD = AB/2 + x，其中x>0时，由于x>0，则“AC + AD < AB”，称为三垂线逆定理。

三垂线定理从图上可以看出，如果三角形ABC的两边上（即AC和AB）之间的垂直距
离（即AD）大于或等于这两边对应的边距离的总和（即AC+AD），则它就是一个有效的三
角形，而如果其中的垂直距离小于这两边的距离的总和，则它就是一个无效的三角形。

因此，可以将三垂线定理和逆定理分别作为有、无效三角形的标准来判断三角形是否
有效，从而进一步研究三角形的形态、角度和等式等特征。

另外，三垂线定理和逆定理在三角形中，也可以作为其他几何要素的判定标准，比如
两个边的总和和第三边的比较等。

这样不仅有助于构建理论，而且也有助于更好地理解和
研究三角形的性质和特征。