阻抗串联电路与导纳并联电路
- 格式:doc
- 大小:88.00 KB
- 文档页数:1



初中物理串联电路与并联电路知识点总结初中物理串联电路与并联电路知识点1、串联电路:把电路元件逐个顺次连接起了就组成了串联电路。
特点:①电流只有一条路径; ②各用电器之间互相影响,一个用电器因开路停止工作,其它用电器也不能工作; ③只需一个开关就能控制整个电路。
串联电路的特点:1、串联电路中电流处处相等。
I=I1=I2 2、串联电路中的总电阻等于各电阻之和。
R=R1+R2 3、串联电路中的总电压等于各电阻两端电压之和。
U=U1+U2 4、串联电路中各电阻两端的电压之比等于电阻之比。
U/R=U1/R1=U2/R2 5、串联电路中各电阻的功率之比等于电阻之比。
P/R=P1/R1=P2/R2电流在分支前和合并后所经过的路径叫做干路;分流后到合并前所经过的路径叫做支路。
特点:①电流两条或两条以上的`路径,有干路、支路之分; ②各用电器之间互不影响,当某一支路为开路时,其它支路仍可为通路; ③干路开关能控制整个电路,各支路开关控制所在各支路的用电器。
1、把电路中的元件并列地接到电路中的两点间。
即若干二端电路元件共同跨接在一对节点之间的连接方式。
这样连成的总体称为并联组合。
其特点是:①组合中的元件具有相同的电压;②流入组合端点的电流等于流过几个元件的电流之和;③线性时不变电阻元件并联时,并联组合等效于一个电阻元件,其电导等于各并联电阻的电导之和,称为并联组合的等效电导,其倒数称为等效电阻;④几个初始条件为零的线性时不变电容元件并联时的'等效电容为;⑤几个初始条件为零的线性时不变电感元件并联时的等效电为;⑥正弦稳态下,几个复数导纳的并联组合的等效导纳为,式中Yk是并联组合中第k个导纳。
并联电路电阻大小的计算公式为1/R=1/R1+1/R2+1/R3+…… (R1、R2、R3……表示各支路电阻大小);若只有两个电阻并联,则有计算公式:R=R1XR2/R1+R2(此公式只能用于两个电阻并联,多个电阻并联只能用上一个公式)。

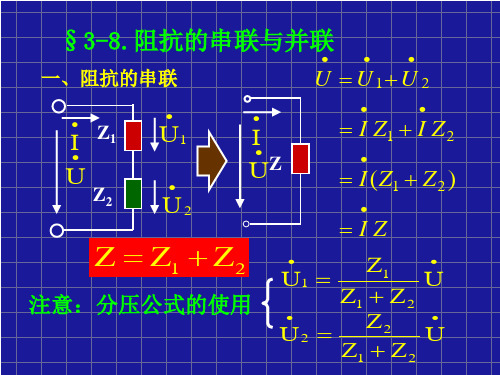
阻抗/导纳的串并联
1. 阻抗(导纳)的串联
以RLC 串联电路为例:
根据相量形式的KVL 和每个元件的VCR:
当X 0,则电路呈感性,当X lt; 0,则电路呈容性,当X = 0 ,电路呈什么性??
推而广之,n 个阻抗串联,其等效阻抗为:
总阻抗公式和分压公式与直流电阻电路形式完全相同!
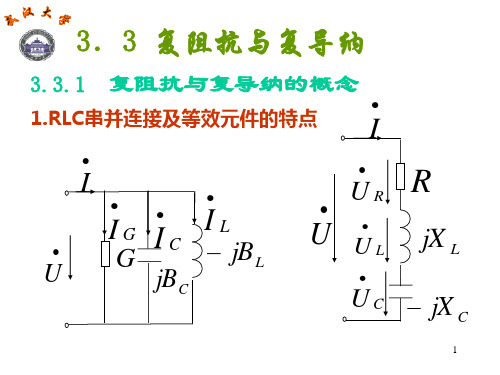
2. 阻抗(导纳)的并联
以RLC 并联电路为例:
根据相量形式的KCL 和每个元件的VCR:
当1/(LC) ω2 ,电路呈感抗;
当1/(LC)=ω2 ,电路呈纯电阻性质;
当1/(LC) lt; ω2 ,电路呈容抗;
推而广之,n 个阻抗并联,其等效阻抗或导纳及各分电流为:
总阻抗公式及分流公式与直流电阻电路条件下形式完全相同!
3. 阻抗和导纳的等效互换
1。
单元电路的网络参量,可以直接根据未归一化网络参量的 定义求得。
也可以根据网络参量间的互换关系,由另一组网络参量转推得到。
一、串联阻抗图 1 串联阻抗由图 1,根据基尔霍夫定律,有:12121I I U U ZI =-⎧⎨=+⎩ (1-1) 1.1 Y 矩阵根据导纳矩阵定义:11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (1.1-1)将式(1-1)代入,有2111011U I Y U Z ===,1112021U I Y U Z ===-,2221011U I Y U Z===-,1222021U I Y U Z===则[]11122122111=11Y Y Y Y Y Z -⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦(1.1-2)1.2 A 矩阵根据转移矩阵定义:11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (1.2-1)将式(1-1)代入,有2111021I U A U ===,211202-U U A Z I ===,2121020I I A U ===,2122021U I A I ===-则[]111221221=01A A Z A A A ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (1.2-2)1.3 S矩阵根据S矩阵和a矩阵的转换关系:[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS S a a a aa a a aZZ ZZZR ZR Z Z R+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤+-=⎢⎥++-+⎢⎥⎣⎦(1.3-1)考虑Z01=Z02情况,此时R=1,则[]2122ZSZ Z⎡⎤=⎢⎥+⎢⎥⎣⎦(1.3-2) 1.4 T矩阵根据S矩阵和T矩阵的转换关系:[]2211212111111(1)(1)41(1)1111STS SSZ RZ R ZR Z R Z Z R RR Z R ZR Z R ZR Z R Z-⎡⎤=⎢⎥-⎣⎦⎡⎤-+-⎢⎥++⎥=⎥+--+--++⎥++++⎢⎥⎣⎦⎡⎤++--=⎥+--+⎥⎦(1.4-1)考虑Z01=Z02情况,此时R=1,则[]2122Z ZTZ Z⎡⎤+-=⎢⎥-⎢⎥⎣⎦(1.4-2)二、并联导纳图 2 并联导纳由图 2,根据基尔霍夫定律,有:12121U U I I YU =⎧⎨+=⎩ (2-1) 2.1 Z 矩阵根据阻抗矩阵定义,有:11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (2.1-1) 将式(2-1)代入,有2111011I U Z I Y===,1112021I U Z I Y ===,2221011I U Z I Y ===,1222021I U Z I Y===(2.1-2)即[]1112212211111ZZ Z Z Z Y ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦(2.1-3)2.2 A 矩阵根据转移矩阵定义:11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (2.2-1)将式(1-1)代入,有2111021I U A U ===,2112020-U U A I ===,212102I I A Y U ===,2122021U I A I ===-则[]1112212210=1AA A A A Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (2.2-2)2.3 S矩阵根据S矩阵和a矩阵的转换关系:[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS Sa a a aa a a aYRYRR YRR YR R YR+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤--=⎢++--⎢⎣⎦⎥⎥(2.3-1)考虑Y01=Y02情况,此时R=1,则[]2122YSY Y⎡⎤-=⎢⎥+-⎢⎥⎣⎦(2.3-2) 2.4 T矩阵根据S矩阵和T矩阵的转换关系:[]2211212111111(1)(1)41(1)1111STS SSYR RYR R YRR YR R YR YR R RR YR R YRR YR R YRR YR R YR-⎡⎤=⎢⎥-⎣⎦⎡⎤+-⎢⎥++⎥=⎥------+--⎢⎥++++⎢⎥⎣⎦⎡⎤+++-=⎥---+⎥⎦(2.4-1)考虑Y01=Y02情况,此时R=1,则[]2122Y YTY Y⎡⎤+=⎢⎥--⎢⎥⎣⎦(2.4-2)三、无耗传输线段图 3 无耗传输线段根据传输线方程的解:00()cos sin ()cos sin L L L L U z U z jI Z z U I z I z j z Z ββββ=+⎧⎪⎨=+⎪⎩(3-1)根据传输线方程的关系,22,,L L z U U I I θβ===-,则12202120cos sin sin cos U U jI Z U I j I Z θθθθ=-⎧⎪⎨=-⎪⎩(3-2) 3.1 Z 矩阵根据阻抗矩阵定义,有:11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (3.1-1)将式(3-2)代入有:212110021cos cot sin I U U Z jZ U I j Z θθθ====- (3.1-2)11120csc I U Z jZ I θ===- (3.1-3)2221001csc I U Z jZI θ===-(3.1-6) 1222002cot I U Z jZ I θ===- (3.1-7)即[]001112002122cot csc csc cot jZ jZ ZZ Z jZ jZ Z Z θθθθ--⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦(3.1-8)3.2 Y 矩阵根据导纳矩阵定义:11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (3.2-1)将式(3-2)代入,根据定义,U 2=0时,将式(3-2)两式相除,有2121101200cos 1cot sin U I I Y j U jI Z Z θθθ====- (3.2-2)根据定义,U 1=0时,由式(3-2_1)有22200cos 1cot sin U I j j U Z Z θθθ=-=-,代入式(3-2_2)有221200011sin (cot )cos sin U U I j j U j Z Z Z θθθθ=--=,进而1112021csc U I Y jU Z θ=== (3.2-3) 根据定义,U 2=0时,由式(3-2_1)有 2221011csc U I Y jU Z θ=== (3.2-4) 根据定义,U 1=0时,由式(3-2_1)有12220200cos 1cot sin U I Y j U jZ Z θθθ====- (3.2-5)由式(3.2-2)-式(3.2-5)有:[]00111221220011cot csc =11csc cot j j Z Z Y Y Y Y Y j j Z Zθθθθ⎡⎤-⎢⎥⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦-⎢⎥(3.2-6)将式(3.1-8)和式(3.2-6)相乘,有 [][]00000000222211cot csc cot csc csc cot 11csc cot 10csc cot 0010csc cot j jZ Z jZ jZ Z Y jZ jZ j j Z Z θθθθθθθθθθθθ⎡⎤-⎢⎥--⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦-⎢⎥⎣⎦⎡⎤-⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦ (3.2-14)根据式(3-2)以及A 矩阵定义,有211102cos I U A U θ===,2112002sin -U U A jZ I θ===,21210201sin I I A jU Z θ===,212202cos U I A I θ===-。