电阻的串联和并联

电阻在串联和并联中的规律和公式
（实用版）
目录
1.串联电路的电阻规律和公式
2.并联电路的电阻规律和公式
3.电阻串联和并联的实际应用
正文
一、串联电路的电阻规律和公式
串联电路是指多个电阻依次排列在同一电路中，电流在各个电阻之间是相等的。

根据欧姆定律，电阻的计算公式为 R=U/I，其中 R 代表电阻，U 代表电压，I 代表电流。

在串联电路中，总电阻等于各电阻之和，即R_total=R1+R2+R3+...+Rn。

二、并联电路的电阻规律和公式
并联电路是指多个电阻同时连接在电路的两个分支上，电压在各个电阻之间是相等的。

根据基尔霍夫定律，并联电路的总电阻公式为
1/R_total=1/R1+1/R2+1/R3+...+1/Rn。

化简后得到
R_total=R1*R2*R3*...*Rn/(R1+R2+R3+...+Rn)。

三、电阻串联和并联的实际应用
电阻串联和并联在实际电路中应用广泛，例如在家庭用电、工业生产等领域。

在串联电路中，电阻值越大，电流越小，总电阻等于各电阻之和。

在并联电路中，电阻值越小，电流越大，总电阻的倒数等于各电阻阻值的倒数之和。

第1页共1页。

电阻的串联知识点1---电阻的串联1、电路中各处电流，即I1＝I2＝I3＝I；2、串联电路两端总电压等于各部分电路两端的电压，即：U＝U1＋U2＋U3；3、串联电路的总电阻，等于各串联电阻，即：R＝R1＋R2＋R3，若是n个相同的电阻R′串联，则R＝n R′；串联的电阻有作用，每个电阻所分担的电压跟它的电阻成；串联电路的总电阻比任何一个导体的电阻都要，串联时相当于导体长度。

例1．阻值为10Ω的电阻R1与阻值为25Ω的电阻R2串联后的总电阻是．若通过R1的电流为0．2A，则通过电阻R2的电流是，R2两端的电压是．例2．R1与R2串联后的总电阻为350Ω，已知电阻R1=170Ω，则电阻R2= Ω．例3．电阻R1、R2串联在电路中，已知R1∶R2=3∶2，则通过两电阻的电流之比I1∶I2= ，电阻两端的电压之比U1∶U2= ．例4．R1=5Ω，R2=10Ω，串联后接到6V的电源上，则R1两端的电U1为，R2两端的电压U2为，U1∶U2= ．例5．电阻R1=30Ω，与电阻R2串联后总电阻为90Ω，则电阻R2为Ω．例6．粗细相同的两根铝导线，长度关系是L1＞L2，串联接入电路后，其电流和两端电压的关系是（）．A．I1＞I2，U1＜U2 B．I1＜I2，U1＞U2 C．I1=I2，U1＞U2 D．I1=I2，U1＜U2例7．串联电路随着用电器的个数增加，其总电阻（）．A．变大 B．变小C．不变 D．无法判断例8．如图1，R1=6Ω，U2=3V，总电压为7V，求：R2为多大？例9．如图2，R1=2Ω，R2=3Ω，电压表的示数为1V．求：R2两端的电压和电源电压．例10．如图3所示的电路，电压U为24V，电流表的示数为1．2A，电压表的示数为6V，则电阻R1阻值为Ω．例11．电阻R1和R2串联后的总电阻是1．5k Ω，接入电路后，R1两端的电压为6V，R2两端的电压为3V，则R1的阻值是Ω．例12．如图4所示，已知R1=6Ω，U∶U2=4∶1，则R2的阻值是Ω，U1∶U2= ．例13．如图5所示的电路，R1的阻值为10Ω，电流表的示数为0．4A，电压表的示数为3．2V．求：R1两端的电压，R2的阻值及电源电压．例14．如图7所示的电路，电源电压为20V，R1=25Ω，电流表的示数为0．25A，求R2的阻值和电压表的示数．图1图2图5图3图4图7课 后 作 业1．如图1所示，小灯泡正常发光时灯丝的电阻是7．5Ω，电压是1．5V ．如果电源电压为4V ，要使小灯泡正常发光，应串联一个变阻器分去电压 V ，并控制电路中的电流为 A ，调节滑动变阻器的阻值为 Ω．2．如图2所示，电流表的示数是0．3A ，灯泡L 的电阻为3Ω，整个电路的电阻为30Ω，那么，灯泡两端的电压为 V ，电压表的示数是 V ．3．将电阻R 1、R 2串联在电路中，已知：R 1=3R 2，总电压为4V ，则R 1两端的电压为（）A ．4VB ．3VC ．2VD ．1V 4．两根长度相同，粗细不同的锰铜丝，把它们串联在电路中，则（ ）． A ．粗的电流大，且电压也大 B ．细的电流大，且电压也大C ．粗的、细的电流一样大，但细的电压大D ．粗的、细的电流一样大，但粗的电压大 5．一段导体的电阻增加3Ω后，接在原电源上，发现通过该导体的电流是原来的4/5，则该导体原来的阻值是多少？6．如图3所示的电路，R 1=20Ω，变阻器R 2的阻值范围为0～40Ω，当变阻器滑片P 移至变阻器的中点时，电流表的示数为0．5A ，那么当变阻器滑片P 移至阻值最大位置时，电流表的示数多大？7．如图4所示的电路中，当变阻器的滑片在向右移动过程中，变阻器连接入电路的阻值将 ，电路中的电流将 ，电阻R 1两端的电压将 ．（填“变大”、“变小”或“不变”）8．如图5所示当滑动变阻器的滑片自左向右移动的过程中，电路的总电阻、电流表示数和电压表示数的变化情况分别是（ ）． A ．变小、变大、不变 B.不变、变大、变小 C ．变大、变小、变小 D ．变大、变大、变大 9．如图6所示的电路，移动滑片P ，使电压表的示数由U 1变化到U 2，已知U 1∶U 2=5∶2，则滑动变阻器滑片移动前后，通过电阻R 的电流之比为（ ）． A.5∶2 B ．2∶5 C ．1∶1 D ．无法判断10．将电阻R 1和R 2组成串联电阻R 1∶R 2=3∶1，如果电路两端的总电压是12V,R 1两的电压 A ．4V B ．3V C ．8V D ．9V 11．某用电器R 1上标有“10Ω 3A ”，另一用电器R 2上标有“50Ω 1．5A ”，串联后接到电源上，为了使其中一个用电器正常工作，电源电压应不超过何值？12．如图7，R 1=10Ω，R 2是阻值为0～40Ω的变阻器，电源电压为12V ．当P 在B 端时，电压表的示数多大？当P 在AB 中点时，电流表、电压表的示数各多大？图3图1图2图4图5图7图6电阻的并联电阻的并联1、并联电路中的总电流 各支路中的电流之和。

电阻并联和串联公式一、电阻串联。

1. 特点。

- 电流：串联电路中各处的电流相等，即I = I_1=I_2=·s = I_n。

- 电压：总电压等于各部分电路电压之和，即U = U_1 + U_2+·s+U_n。

2. 电阻关系（串联电路总电阻公式）- 根据U = IR，U_1=I_1R_1，U_2 = I_2R_2等，因为I = I_1 = I_2且U=U_1 + U_2，所以IR = I_1R_1+I_2R_2，即R = R_1+R_2+·s+R_n。

串联电路的总电阻等于各串联电阻之和。

例如，有两个电阻R_1 = 3Ω，R_2=5Ω串联，总电阻R = R_1 +R_2=3Ω+ 5Ω = 8Ω。

二、电阻并联。

1. 特点。

- 电压：并联电路中各支路两端的电压相等，即U = U_1=U_2=·s = U_n。

- 电流：总电流等于各支路电流之和，即I = I_1+I_2+·s+I_n。

2. 电阻关系（并联电路总电阻公式）- 根据I=(U)/(R)，I_1=(U_1)/(R_1)，I_2=(U_2)/(R_2)等，因为U = U_1 = U_2且I = I_1+I_2，所以(U)/(R)=(U_1)/(R_1)+(U_2)/(R_2)，即(1)/(R)=(1)/(R_1)+(1)/(R_2)+·s+(1)/(R_n)。

- 对于两个电阻R_1和R_2并联的情况，总电阻R=(R_1R_2)/(R_1 + R_2)。

例如，R_1 = 6Ω，R_2 = 3Ω并联，总电阻R=(6Ω×3Ω)/(6Ω + 3Ω)=(18Ω)/(9Ω)=2Ω。

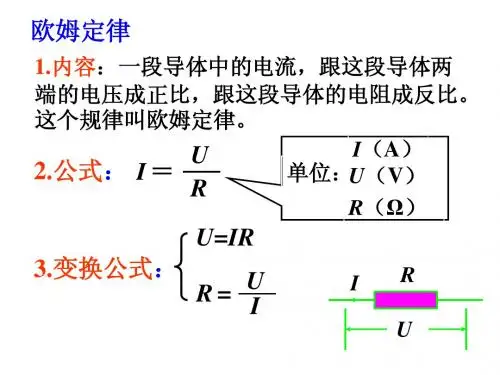
电阻的串并联与电流的分配电阻是电路中常用的元件之一，它用来限制电流的流动。

在电路中，电阻的串并联以及电流的分配是一项基础且重要的知识。

本文将介绍电阻的串并联以及电流的分配原理、公式推导以及应用案例。

一、电阻的串联与并联1. 串联电阻串联电阻是指将多个电阻依次连接在电路中，形成电流依次流过各个电阻的电路连接方式。

根据基尔霍夫电压定律，串联电阻的总电阻等于各个电阻的电阻之和。

假设有两个电阻 R1 和 R2 串联在一起，它们的电流分别为 I1 和 I2，电源电压为 V，根据 Ohm 定律可得：V = I1 * R1 + I2 * R2根据基尔霍夫电压定律可得：V = (I1 + I2) * R_eq其中 R_eq 为串联电阻的等效电阻。

由上述等式可得：R_eq = R1 + R22. 并联电阻并联电阻是指将多个电阻同时连接在电路中，各个电阻之间共享电压源，电流分别流过各个电阻的电路连接方式。

根据基尔霍夫电流定律，并联电阻的总电流等于各个电阻电流之和。

假设有两个电阻 R1 和 R2 并联在一起，它们的电流分别为 I1 和 I2，根据基尔霍夫电流定律可得：I = I1 + I2根据 Ohm 定律可得：I = V / (R1 + R2)由上述等式可得：1/R_eq = 1/R1 + 1/R2二、电流的分配在并联电路中，电流会根据各个分支的电阻大小进行分配。

根据欧姆定律，电流和电阻成反比例关系，电流会优先流过电阻较小的分支。

假设有两个并联电路分支，分别含有电阻 R1 和电阻 R2，电源电压为 V，根据 Ohm 定律可得：I1 = V / R1I2 = V / R2其中 I1 和 I2 分别为各个分支的电流。

根据以上公式，当 R1 < R2 时，电流 I1 将大于 I2；当 R1 > R2 时，电流 I1 将小于 I2。

三、应用案例1. 电路中的灯泡假设一个电路中有三个灯泡串联，分别为 R1、R2 和 R3。

电阻的串并联电阻是电学中的基本元件之一，广泛应用于电路中。

在电路中，电阻可以以串联或并联的方式连接，分别称为电阻的串联和并联。

一、电阻的串联电阻的串联是指将多个电阻依次连接起来，形成一个回路。

在串联电路中，电流只有一条通路可走，电阻依次排列在该通路上。

串联电阻的总电阻为各个电阻值的代数和。

设有电阻R1、R2、R3依次串联，则串联电阻RT的计算公式为：RT = R1 + R2 + R3串联电路中，电流在电阻之间产生的压差会根据电阻的大小而分配。

根据欧姆定律，电流在不同电阻之间的电压满足以下关系：U1 = IR1U2 = IR2U3 = IR3其中U1、U2、U3表示电阻R1、R2、R3两端的电压，I为串联电路的总电流。

二、电阻的并联电阻的并联是指将多个电阻并排连接，形成一个平行的分支。

在并联电路中，电压相同，电流分担在各个分支之间。

并联电阻的总电阻为各个电阻值的倒数之和的倒数。

设有电阻R1、R2、R3并联，则并联电阻RP的计算公式为：1/RP = 1/R1 + 1/R2 + 1/R3并联电路中，各个电阻上的电压相同，电流根据电阻大小进行分担。

根据欧姆定律，电流在并联电阻上的分担满足以下关系：I = I1 + I2 + I3其中I1、I2、I3为分别通过电阻R1、R2、R3的电流。

三、串并联的应用串联和并联电路广泛应用于各个领域，例如家庭用电、通信系统、电子电路等。

在家庭用电中，常见的电器设备往往采用并联电路连接。

由于并联电路中电压相同，当一个设备发生故障时，不会影响其他设备的正常工作。

在通信系统中，电阻的串联和并联用于阻止电流的干扰，确保通信信号的稳定传输。

在电子电路中，串联电阻常用于限制电流大小，保护其他元件不受损坏；并联电阻则用于调节电路的电压，实现电路的稳定工作。

总结：电阻的串联和并联是电路中常见的连接方式。

串联电阻的总电阻为各个电阻值之和，电流依次通过各个电阻；并联电阻的总电阻为各个电阻的倒数之和的倒数，电压相同，电流分担在各个分支上。

电阻的串联和并联1. 电阻的定义电阻（Resistance，符号R）是电路元件对电流的阻碍作用，是电路中电子流动的障碍。

电阻的单位是欧姆（Ohm，符号Ω），常用的单位还有千欧（kΩ）和兆欧（MΩ）。

2. 电阻的串联2.1 串联电路的定义串联电路是指将多个电阻依次连接在一起，形成一个电路。

在串联电路中，电流只有一条路径可以流通，因此电路中的电流在各个电阻中是相同的。

2.2 串联电路的总电阻在串联电路中，各个电阻的总电阻（Req）等于各个电阻的阻值（R1、R2、…、Rn）之和。

即：[ Req = R1 + R2 + … + Rn ]2.3 串联电路的特点（1）电流相等：在串联电路中，通过各个电阻的电流相等。

（2）电压分配：在串联电路中，各个电阻两端的电压之比等于它们的阻值之比。

（3）功率分配：在串联电路中，各个电阻消耗的功率之比等于它们的阻值之比。

3. 电阻的并联3.1 并联电路的定义并联电路是指将多个电阻并排连接在一起，形成一个电路。

在并联电路中，各个电阻的两端电压相同，电流在各个电阻之间分流。

3.2 并联电路的总电阻在并联电路中，各个电阻的总电阻（Req）可以通过以下公式计算：[ = + + … + ]3.3 并联电路的特点（1）电压相等：在并联电路中，各个电阻的两端电压相等。

（2）电流分配：在并联电路中，通过各个电阻的电流之比等于它们的阻值之比的倒数。

（3）功率分配：在并联电路中，各个电阻消耗的功率之比等于它们的阻值之比的倒数。

4. 串联和并联电路的应用4.1 串联电路的应用串联电路在实际应用中主要用于测量电压、电流和功率等。

例如，电压表、电流表和电阻表等都是基于串联电路的原理制成的。

4.2 并联电路的应用并联电路在实际应用中主要用于测量电压和电流等。

例如，多用电表就是基于并联电路的原理制成的。

5. 总结本文介绍了电阻的串联和并联电路的基本概念、公式和特点。

掌握了这些知识，读者可以更好地理解和应用电阻串联和并联电路，为电路设计和分析提供帮助。

电阻在串联和并联中的规律和公式
（实用版）
目录
1.串联电路的电阻规律和公式
2.并联电路的电阻规律和公式
3.电阻在串联和并联中的实际应用
正文
一、串联电路的电阻规律和公式
串联电路是指多个电阻依次排列在同一电路中，电流在各个电阻之间是相同的。

根据欧姆定律，电阻的计算公式为 R=U/I，其中 R 代表电阻，U 代表电压，I 代表电流。

在串联电路中，总电阻等于各部分电路电阻之和，即 R_total=R1+R2+R3+...+Rn。

二、并联电路的电阻规律和公式
并联电路是指多个电阻同时连接在电路的两个分支上，电压在各个电阻之间是相同的。

根据基尔霍夫定律，电阻的计算公式为
1/R_total=1/R1+1/R2+1/R3+...+1/Rn，即
R_total=1/(1/R1+1/R2+1/R3+...+1/Rn)。

三、电阻在串联和并联中的实际应用
在实际应用中，串联电路和并联电路有着不同的特点。

串联电路中，电阻值相加，总电阻随着电阻值的增加而增加；并联电路中，电阻值相乘，总电阻随着电阻值的减小而减小。

因此，在需要限制电流的场合，通常采用串联电路；在需要提高电压的场合，通常采用并联电路。

总之，电阻在串联和并联电路中的规律和公式分别为：串联电路中，总电阻等于各部分电路电阻之和；并联电路中，总电阻的倒数等于各电阻阻值的倒数之和。

电阻并联和串联电阻值1. 引言电阻是电路中常见的元件之一，它用来限制电流的流动。

在电路设计和分析中，我们经常需要计算并联和串联电阻值。

本文将介绍什么是并联和串联电阻以及如何计算它们的值。

2. 并联电阻并联电阻是指将多个电阻以平行的方式连接在一起的情况。

在并联电路中，每个电阻都有相同的电压，而总电流等于各个分支电流之和。

假设有两个并联的电阻R1和R2，它们的等效电阻记作Rp。

根据欧姆定律，我们可以得到以下公式：1/Rp = 1/R1 + 1/R2如果有更多的并联电阻R3、R4、…、Rn，可以推广上述公式为：1/Rp = 1/R1 + 1/R2 + ... + 1/Rn通过以上公式，我们可以计算出并联电路中的等效电阻值Rp。

3. 串联电阻串联电阻是指将多个电阻以连续的方式连接在一起的情况。

在串联电路中，总电压等于各个电阻之间的电压之和，而总电流等于各个电阻上的电流之和。

假设有两个串联的电阻R1和R2，它们的等效电阻记作Rs。

根据欧姆定律，我们可以得到以下公式：Rs = R1 + R2如果有更多的串联电阻R3、R4、…、Rn，可以推广上述公式为：Rs = R1 + R2 + ... + Rn通过以上公式，我们可以计算出串联电路中的等效电阻值Rs。

4. 示例为了更好地理解并联和串联电阻的计算方法，我们来看一个具体的示例。

假设有一个并联电路，其中有三个并联的电阻分别为10欧姆、20欧姆和30欧姆。

我们希望计算出这个并联电路的等效电阻。

根据并联公式：1/Rp = 1/R1 + 1/R2 + 1/R3将具体数值代入公式中：1/Rp = 1/10 + 1/20 + 1/30化简后得到：1/Rp = (3/30) + (2/30) + (1/30)继续化简：1/Rp = 6/30最后得到：Rp = 30/6 = 5欧姆因此，这个并联电路的等效电阻为5欧姆。

接下来，让我们来计算一个串联电路的等效电阻。

假设有一个串联电路，其中有四个串联的电阻分别为5欧姆、10欧姆、15欧姆和20欧姆。

串联电阻与并联电阻的计算方法电阻是电路中常见的元件之一，用来限制电流的流动。

在电路中，我们经常会遇到串联电阻和并联电阻的问题。

本文将介绍串联电阻与并联电阻的计算方法。

一、串联电阻的计算方法串联电阻是指将多个电阻按照顺序连接在一起，电流依次通过各个电阻。

串联电阻的总电阻等于各个电阻的电阻值之和。

设有n个串联电阻R1，R2，…，Rn，其总电阻为RT，则串联电阻的计算公式为：RT = R1 + R2 + … + Rn例如，有三个串联电阻分别为2Ω、3Ω和4Ω，则它们的总电阻为：RT = 2Ω + 3Ω + 4Ω = 9Ω二、并联电阻的计算方法并联电阻是指将多个电阻同时连接在一起，电压相同，电流按照分流原理分别通过各个电阻。

并联电阻的总电阻等于各个电阻电阻值的倒数之和的倒数。

设有n个并联电阻R1，R2，…，Rn，其总电阻为RP，则并联电阻的计算公式为：1/RP = 1/R1 + 1/R2 + … + 1/Rn例如，有三个并联电阻分别为2Ω、3Ω和4Ω，则它们的总电阻为：1/RP = 1/2Ω + 1/3Ω + 1/4Ω = 7/12ΩRP = 12Ω/7三、串联电阻与并联电阻的应用举例1. 串联电阻的应用假设我们有一个电路，其中有一根电线负载了多个电器，每个电器都有不同的电阻值。

我们希望计算整个电路的电阻，以确定电流大小。

这种情况下，就需要使用串联电阻的计算方法。

2. 并联电阻的应用在某个电路中，我们希望将多个电源连接在一起，以提供更大的电流输出。

为了保证电流均匀分配，我们使用并联电阻的方法连接电源，以达到平衡电流的效果。

在这种情况下，就需要使用并联电阻的计算方法。

四、电阻的选择和设计在实际应用中，我们需要根据电路的需求来选择和设计电阻。

如果需要调节电路的电流或电压，可以改变电阻的数值来实现。

通过合理选择和设计电阻，我们可以达到满足电路要求的效果。

总结：本文介绍了串联电阻与并联电阻的计算方法。

串联电阻的总电阻等于各个电阻的电阻值之和，而并联电阻的总电阻等于各个电阻电阻值的倒数之和的倒数。

电阻的串联并联电阻是电路中常见的一种元件，它用于限制电流的流动。

在电路中，电阻可以通过串联或并联的方式连接，以达到不同的电路效果和功能。

本文将就电阻的串联和并联进行详细介绍。

一、电阻的串联连接电阻的串联连接是指将多个电阻依次连接在一起，电流依次流经各个电阻。

串联连接的特点是电流在各个电阻之间是相同的，而总电阻等于各个电阻之和。

例如，如果有三个电阻R1、R2和R3，它们的阻值分别为10欧姆、20欧姆和30欧姆。

将它们串联连接起来，电流首先流经R1，然后流经R2，最后流经R3。

根据串联连接的特点，电流在各个电阻之间是相同的，假设电流为I。

根据欧姆定律，可以得到以下关系：电压V1 = R1 * I电压V2 = R2 * I电压V3 = R3 * I根据电压的分配规律，总电压等于各个电压之和，所以有：V总 = V1 + V2 + V3 = R1 * I + R2 * I + R3 * I根据欧姆定律，电压等于电流乘以电阻，所以有：V总 = (R1 + R2 + R3) * I由此可得，串联连接的电阻总和等于各个电阻之和，即：R总 = R1 + R2 + R3二、电阻的并联连接电阻的并联连接是指将多个电阻同时连接在一起，电流会分别流经各个电阻。

并联连接的特点是各个电阻之间的电压相同，而总电阻的倒数等于各个电阻倒数之和的倒数。

例如，如果有三个电阻R1、R2和R3，它们的阻值分别为10欧姆、20欧姆和30欧姆。

将它们并联连接起来，电压在各个电阻之间是相同的，假设电压为V。

根据欧姆定律，可以得到以下关系：I1 = V / R1I2 = V / R2I3 = V / R3根据电流的分配规律，总电流等于各个电流之和，所以有：I总 = I1 + I2 + I3 = V / R1 + V / R2 + V / R3根据欧姆定律，电流等于电压除以电阻，所以有：I总 = V * (1/R1 + 1/R2 + 1/R3)由此可得，并联连接的电阻的倒数等于各个电阻倒数之和的倒数，即：1/R总 = 1/R1 + 1/R2 + 1/R3三、串联与并联的比较串联和并联是电路中常用的两种电阻连接方式，它们在电路中发挥不同的作用。

电阻的串联与并联电阻是电路中常见的元件，它用于限制电流的流动。

在电路中，电阻可以通过串联和并联的方式连接，以达到不同的电路效果。

本文将介绍电阻的串联和并联及其相关特性。

一、串联电阻串联电阻是指将电阻以直线方式连接在一起，其中的电流依次通过每个电阻。

在串联电路中，电流只有一个路径可以流动，因此串联电阻的总电阻等于各个电阻的阻值之和。

换句话说，串联电阻的总阻值等于R1+R2+R3+...+Rn（R1至Rn分别代表每个电阻的阻值）。

串联电阻的总电流是相同的，因为电流只有一个路径可以流动。

同时，各个电阻所承受的电压与它们的阻值成正比。

例如，如果某个串联电路中有两个电阻，R1和R2，阻值分别为10欧姆和20欧姆，总电压为12伏特，那么R1将承受4伏特的电压，而R2将承受8伏特的电压。

二、并联电阻并联电阻是指将电阻以平行方式连接在一起，其中的电流分流通过各个电阻。

在并联电路中，电流可以选择不同的路径流动，因此并联电阻的总电阻是各个电阻阻值的倒数之和再取倒数。

换句话说，若有n 个并联电阻，它们的阻值分别为R1、R2、R3...Rn，则并联电阻的总阻值等于1/（1/R1+1/R2+1/R3+...+1/Rn）。

并联电阻的总电压是相同的，因为电压在各个电阻之间分配。

此外，各个电阻所承受的电流与它们的阻值成反比。

举例来说，如果某个并联电路中有两个电阻，R1和R2，阻值分别为10欧姆和20欧姆，总电流为2安培，那么R1将承受1安培的电流，而R2将承受2安培的电流。

三、串联与并联的比较串联电阻的总阻值是各个电阻阻值之和，而并联电阻的总阻值是各个电阻阻值的倒数之和再取倒数。

因此，在串联电路中，总阻值始终大于任何一个电阻的阻值，而在并联电路中，总阻值始终小于任何一个电阻的阻值。

另外，串联电阻的总电流是相同的，各个电阻的电压根据它们的阻值分配。

而并联电阻的总电压是相同的，各个电阻的电流根据它们的阻值分配。

四、实际应用串联和并联电阻在电子电路中有广泛的应用。

串联与并联电路电阻的组合方式电阻是电路中常见的元件之一，它在电路中起到调节电流和电压的作用。

在实际应用中，我们经常会遇到需要多个电阻组合的情况，以达到特定的电阻值或起到特定的电路效果。

串联和并联是两种常见的电阻组合方式，本文将详细介绍串联和并联电路电阻的组合方式及其特点。

一、串联电路电阻的组合方式串联电路是将多个电阻依次连接在一起，电流通过每个电阻时都要通过下一个电阻。

串联电路中，各个电阻之间的电流相等，而总电阻等于各个电阻之和。

例如，我们有三个电阻分别为R1、R2和R3，它们依次连接在一起，组成了一个串联电路。

根据串联电路的特点，我们可以得到总电阻Rt的计算公式：Rt = R1 + R2 + R3串联电路中，电阻值越大，总电阻将越大。

此外，电流在串联电路中是恒定的，即经过每个电阻的电流相等。

二、并联电路电阻的组合方式并联电路是将多个电阻同时连接在电路中的分支中，电流可以选择通过其中的任意一个电阻。

并联电路中，各个电阻之间的电压相等，而总电阻是各个电阻电阻值的倒数之和的倒数。

以两个电阻R1和R2的并联电路为例，我们可以得到总电阻Rt的计算公式：1 / Rt = 1 / R1 + 1 / R2从并联电路的特点可以看出，电阻值越小，总电阻将越小。

与串联电路不同，并联电路中的电压是恒定的，即经过每个电阻的电压相等。

三、串联与并联电路电阻的应用特点根据串联电路和并联电路的特点，我们可以在实际应用中选择合适的电阻组合方式。

串联电路适合在需要增加总电阻的情况下使用。

例如，在电子电路中，我们可能需要限制电流的流动，此时可以采用串联电阻的方式来增加电阻值，以降低电流。

同时，串联电路还可以起到分压的作用，即将电压按照一定比例分配给各个电阻。

然而，并联电路则适合在需要减小总电阻的情况下使用。

例如，在家庭配电系统中，我们希望电器设备得到更大的电流供应，此时可以采用并联电阻的方式来降低电阻值，以提高电流。

同时，并联电路还可以起到分流的作用，即将电流按照一定比例分配给各个电阻。

电路中的电阻串联和并联电阻的等效问题在电路中，电阻是一个重要的元件。

在电路设计和分析中，经常会遇到电阻串联和并联电阻的等效问题。

本文将详细讨论电路中电阻串联和并联的概念、计算方法以及等效电阻的计算。

1. 电阻串联的概念和计算方法电阻串联是指将两个或多个电阻按顺序连接在一起的方式。

当电阻串联时，电流依次通过每个电阻。

电阻串联的总电阻可以通过将每个电阻的阻值相加来计算。

假设有两个电阻R1和R2，它们串联在一起，总电阻记为RT。

那么，总电阻的计算公式如下：RT = R1 + R22. 电阻并联的概念和计算方法电阻并联是指将两个或多个电阻同时连接在电路中的方式。

当电阻并联时，电流会分流经过各个电阻。

电阻并联的总电阻可以通过将每个电阻的倒数相加后再取倒数来计算。

假设有两个电阻R1和R2，它们并联在一起，总电阻记为RP。

那么，总电阻的计算公式如下：1/RP = 1/R1 + 1/R2电阻串联和并联的概念和计算方法可以扩展到多个电阻的情况。

例如，对于三个电阻R1、R2和R3的串联电路，总电阻的计算公式为：RT = R1 + R2 + R3对于三个电阻R1、R2和R3的并联电路，总电阻的计算公式为：1/RP = 1/R1 + 1/R2 + 1/R33. 电阻串联和并联的等效问题在电路中，经常需要求解电阻串联和并联电阻的等效问题。

等效问题是指将一个复杂的电路转化为一个简化的电路，该简化电路具有相同的电流电压特性。

电阻串联和并联的等效问题可以通过计算总电阻来实现。

对于电阻串联，可以将多个串联的电阻替换为一个等效电阻。

等效电阻的值与串联的电阻之和相等。

通过使用等效电阻，可以简化电路的分析和计算。

对于电阻并联，可以将多个并联的电阻替换为一个等效电阻。

等效电阻的值可以通过并联电阻的倒数之和再取倒数来计算。

同样地，使用等效电阻可以简化电路的分析和计算。

4. 实例分析现在我们来看一个具体的例子，以帮助理解电阻串联和并联的计算。

串联和并联的电阻
电阻是电路中最常用的一种组件，有两种不同的接地方式：串联和并联。

串联和并联电阻具有不同的功能和特点。

串联接地是将不同阻值的电阻物理连接在一起，它们上面的电流相同，电压则是按电阻值比例分配。

例如，如果一个电路中有一个电阻为10Ω和一个电阻为20Ω，则它们的总电阻值是30Ω，其电压分配为10Ω的12V和2Ω的6V。

串联电阻的优点是可以减小它们的总电阻值，从而减小系统的总电阻值。

并联接地是将相同阻值的电阻物理连接在一起，它们两者的电压相同，但电流则以电阻的个数为比例分配，这就是所谓的阻值共享。

例如，如果一个电路中有两个10Ω电阻，总阻值是10Ω，电压是12V，电流分配为10V和2V。

并联电阻的优点是可以增加它们的总阻值，从而增加系统的总阻值。

在电子电路设计中，有时需要使用串联和并联接地来满足电路的各种需求。

例如，有时候可以使用一组串联的电阻来降低系统的总电阻，减少电流的损耗，从而提高电路的效率。

并联电阻也可以用来实现一些其他的目的，例如电路的功率分配，增加系统的稳定性等等。

因此，串联和并联的电阻在电子电路设计中非常重要，可以帮助我们达到我们想要的电路特性，从而实现一些更复杂的功能。