第二课时、电阻的串联和并联

《电阻的串联与并联》知识清单一、电阻的基本概念电阻是电学中一个非常重要的概念，它是指对电流的阻碍作用。

电阻的大小用电阻值来表示，单位是欧姆（Ω）。

电阻的存在会导致电流在通过时产生能量损耗，表现为发热等现象。

电阻的大小取决于多个因素，包括材料的电阻率、导体的长度、横截面积以及温度等。

一般来说，材料的电阻率越大、导体长度越长、横截面积越小，电阻就越大；而温度升高时，大多数金属的电阻会增大，而一些半导体的电阻则会减小。

二、电阻的串联1、定义电阻的串联是指将多个电阻依次首尾相连，使电流依次通过这些电阻。

2、特点（1）电流处处相等：在串联电路中，通过每个电阻的电流大小是相同的。

（2）总电阻增大：串联电路的总电阻等于各个电阻之和，即 R 总＝ R1 ＋ R2 ＋ R3 ＋……（3）分压作用：各个电阻两端的电压与电阻值成正比，电阻越大，分担的电压越大。

3、计算串联电路总电阻的计算可以通过简单的相加来实现。

例如，有三个电阻分别为 R1 ＝5Ω，R2 ＝10Ω，R3 ＝15Ω，那么串联后的总电阻R 总＝ 5 ＋ 10 ＋ 15 ＝30Ω。

4、实际应用在实际生活中，电阻的串联常用于分压电路，例如在一些需要特定电压的电子设备中，通过串联不同阻值的电阻来获得所需的电压。

三、电阻的并联1、定义电阻的并联是指将多个电阻的两端分别连接在一起，使电流能够同时通过这些电阻。

2、特点（1）电压处处相等：在并联电路中，每个电阻两端的电压是相同的。

（2）总电阻减小：并联电路的总电阻的倒数等于各个电阻倒数之和，即 1/R 总＝ 1/R1 ＋ 1/R2 ＋ 1/R3 ＋……（3）分流作用：通过各个电阻的电流与电阻值成反比，电阻越小，通过的电流越大。

3、计算并联电路总电阻的计算相对复杂一些。

例如，有两个电阻 R1 ＝2Ω，R2 ＝4Ω，它们并联后的总电阻可以通过以下公式计算：1/R 总＝ 1/2＋ 1/4 ＝ 3/4，所以 R 总＝4/3Ω。

电阻的串联和并联关系电阻串联和并联是电路中常见的两种连接方式。

了解电阻的串联和并联关系对于电路设计和故障排查都非常重要。

本文将详细介绍电阻的串联和并联关系以及它们的特点和计算方法。

一、电阻的串联关系电阻的串联是指将多个电阻依次连接起来，电流在电路中顺序通过这些电阻。

串联连接的电阻形成了一个更大的总电阻。

1. 特点：- 串联电阻的总电阻等于各个电阻之和。

假设有两个串联的电阻R1和R2，总电阻Rt可以表示为：Rt = R1 + R2。

- 串联电阻中的电流在各个电阻之间是相等的，即电流保持稳定。

这是因为串联电路中的电流只有一条路径可以流动。

- 串联电路中的电压分配是根据电阻的比例来分配的。

较大的电阻将消耗更多的电压，而较小的电阻将消耗较少的电压。

2. 计算方法：- 对于只有两个串联电阻R1和R2的电路，总电阻Rt可以通过简单相加得到：Rt = R1 + R2。

- 对于多个电阻的串联电路，可以依次将各个电阻的阻值相加得到总电阻。

二、电阻的并联关系电阻的并联是指将多个电阻同时连接在一个节点上，电流在电路中同时通过这些电阻。

并联连接的电阻形成了一个更小的总电阻。

1. 特点：- 并联电阻的总电阻可以通过公式计算得到。

假设有两个并联的电阻R1和R2，总电阻Rt可以表示为：1/Rt = 1/R1 + 1/R2。

- 并联电路中的电压是相等的，各个并联电阻之间的电压相同。

这是因为并联电路中的电流可以根据分支电阻的不同选择流动路径。

- 并联电路中的电流分配是根据电阻的倒数比例来分配的。

较小的电阻将消耗更多的电流，而较大的电阻将消耗较少的电流。

2. 计算方法：- 对于只有两个并联电阻R1和R2的电路，可以使用公式：1/Rt = 1/R1 + 1/R2来计算总电阻Rt。

- 对于多个电阻的并联电路，可以使用类似的公式计算总电阻。

总结：电阻的串联和并联关系在电路中都起着重要作用。

串联电阻形成更大的总电阻，而并联电阻形成更小的总电阻。

电阻的串联和并联教案第一篇：电阻的串联和并联教案一、电阻的串联如果电路中有两个或两个以上电阻一个接一个地顺序相连，并且在这些电阻中通过同一电流，则这样的连接方式称为电阻的串联。

在电路中，电阻的连接形式是多种多样的，其中最简单和最常用的是串联与并联。

一、电阻的串联如果电路中有两个或两个以上电阻一个接一个地顺序相连，并且在这些电阻中通过同一电流，则这样的连接方式称为电阻的串联。

图1(a)所示为N个电阻串联的电路。

图1电阻的串联N个电阻串联可用一个等效电阻R来代替，如图1(b)所示，等效的条件是在同一电压U的作用下电流I保持不变。

等效电阻等于各个串联电阻之和，即eq(1)显然，等效电阻Req必大于任一个串联的电阻。

串联电阻上的电压有如下分压公式(2)可见，串联电阻上电压的分配与电阻成正比。

式(2)称为分压公式。

电阻串联的应用很多。

譬如在负载的额定电压低于电源电压的情况下，通常需要与负载串联一个电阻，以降落一部分电压。

有时为了限制负载中通过过大的电流，也可以与负载串联一个限流电阻。

如果需要调节电路中的电流时，一般也可以在电路中串联一个变阻器来进行调节。

另外，改变串联电阻的大小可以得到不同的输出电压。

二、电阻的并联如果电路中有两个或两个以上电阻连接在两个公共的结点之间，则这样的连接方式称为电阻的并联。

在各个并联支路（电阻）上的电压为同一电压。

图2(a)所示是N个电阻并联的电路。

图2电阻的并联N个电阻并联也可用一个等效电阻R来代替，如图2(b)所示。

等效电导等于并eq联的各电导之和，即(3)或(4)电阻并联时各电阻中的电流为：(5)可见，并联电阻上电流的分配与电导成正比，即与电阻成反比。

当其中某个电阻较其他电阻大很多时，通过它的电流就较其他电阻上的电流小很多，因此，这个电阻的分流作用常可忽略不计。

一般负载都是并联运用的。

负载并联运用时，它们处于同一电压之下，任何一个负载的工作情况基本上不受其他负载的影响。

并联的负载电阻愈多（负载增加），则总电阻愈小，电路中总电流和总功率也就愈大。

电阻的串联与并联规律电阻是电路中常见的元件之一，它可以用来控制电路中的电流和电压。

在电路中，电阻可以通过串联和并联的方式连接在一起。

本文将探讨电阻的串联和并联规律，并介绍它们在电路中的应用。

一、串联电阻规律串联电阻是指将多个电阻依次连接在一起，形成一个闭合的电路。

在串联电路中，电流会依次通过每个电阻，因此对于串联电阻的总电阻，可以使用欧姆定律来计算。

根据欧姆定律，电阻与电流和电压之间存在线性关系，即电阻R等于电压U与电流I之比，即R=U/I。

当电流通过串联电阻时，总电压分为各个电阻上的电压之和，即U=U1+U2+...+Un，根据欧姆定律，可以推导出串联电阻的总电阻Rt等于各个电阻之和，即Rt=R1+R2+...+Rn。

例如，有三个电阻分别为R1，R2，R3，它们依次串联在一起。

电流I从电源进入串联电路，然后依次经过R1，R2，R3。

根据串联电阻的规律，我们可以得出总电阻Rt等于R1+R2+R3。

串联电阻的特点是电流在各个电阻上是相等的，而电压则分担在每个电阻上。

这意味着电流通过串联电路时，阻值较大的电阻会阻碍电流的流动，因此整个电路的总电阻会增加。

二、并联电阻规律并联电阻是指将多个电阻同时连接在电路中，其共同点是两端的电势相同。

在并联电路中，电流会被分到各个电阻上，因此对于并联电阻的总电阻，可以使用欧姆定律来计算。

根据欧姆定律，电阻与电流和电压之间存在线性关系，即电阻R等于电压U与电流I之比，即R=U/I。

当电流通过并联电阻时，总电流等于各个电阻上的电流之和，即I=I1+I2+...+In，根据欧姆定律，我们可以推导出并联电阻的总电阻Rt等于各个电阻电阻值的倒数之和的倒数，即1/Rt=1/R1+1/R2+...+1/Rn。

例如，有三个电阻分别为R1，R2，R3，它们并联在一起。

电压U施加在并联电路上，然后通过R1，R2，R3并返回电源。

根据并联电阻的规律，我们可以得出总电阻Rt等于1/(1/R1+1/R2+1/R3)。

电阻的串联与并联关系电阻在电路中起到控制电流的作用，而电阻的串联与并联则是对多个电阻进行连接的方式。

了解电阻的串联与并联关系对于电路设计与分析非常重要。

一、电阻的串联连接电阻的串联连接是指将多个电阻按照一定顺序连接起来，电流依次通过每个电阻。

串联连接时，多个电阻之间没有分支，形成了一个电阻的总和。

以两个电阻R1和R2的串联连接为例，其电路图如下所示：```—————[R1]—————[R2]—————```在串联连接的电路中，总电阻等于各个电阻之和：R = R1 + R2总电阻的增加使得电流减小，因为电流与电阻成反比。

二、电阻的并联连接电阻的并联连接是指将多个电阻同时连接在电路中，各个电阻之间具有相同的电压。

并联连接时，多个电阻通过并联节点共享电流。

以两个电阻R1和R2的并联连接为例，其电路图如下所示：```—————[R1]—————|—————[R2]—————```在并联连接的电路中，总电阻满足以下计算公式：1/R = 1/R1 + 1/R2总电阻的计算是通过倒数求和得到的。

总电阻的减小使得电流增加，因为电流与电阻成正比。

三、串联与并联关系的实际应用串联与并联连接在电路设计和应用中都有各自的优势和应用场景。

1. 串联连接的应用：- 串联连接可以进行电阻值的叠加，可以实现灵活的电阻调节。

- 在电路中需要分配不同电压给各个电阻时，可以采用串联连接的方式。

- 串联连接可以降低电流，适用于需要控制电流大小的场合。

2. 并联连接的应用：- 并联连接能够分摊电流，适用于需要大电流供应的场合。

- 并联连接可以降低总电阻，提高电路的效率。

- 在需要使各个电阻获得相同电压的情况下，可以采用并联连接。

除了串联与并联之外，电阻还可能存在一些特殊的连接方式，如星型连接和三角形连接。

在实际电路设计中，根据不同的需求选择合适的连接方式可以充分发挥电阻的作用。

总结：电阻的串联与并联关系对电路的设计和分析有重要影响。

串联连接使得电阻值叠加，电流依次通过各个电阻；并联连接能够分摊电流，降低总电阻。

电阻的串联与并联实验电阻串联与并联实验是电路实验中的基础内容之一，通过这个实验可以了解电阻在串联和并联电路中的特性变化，进而深入理解电路的原理。

本文将介绍电阻串联与并联实验的步骤、实验装置以及实验结果的分析。

一、实验步骤1. 准备实验装置：实验时需要用到直流电源、电阻箱、万用表和导线等设备和材料。

将直流电源接通并设置适当的电压，将电阻箱调至所需的电阻值，准备好连接电路所需的导线。

2. 串联实验：将两个或多个电阻依次连接在同一个回路中，电流顺序通过它们。

连接电路时，将电阻箱的正极与直流电源的正极用一根导线连接，将第一个电阻的另一端与第二个电阻的一端用一根导线连接，以此类推，最后将最后一个电阻的另一端与直流电源的负极用一根导线连接。

用万用表测量并记录电路中的总电流和总电压。

3. 并联实验：将两个或多个电阻同时连接在电路中，电流分别通过它们。

连接电路时，将电阻箱的正极与直流电源的正极用一根导线连接，将每个电阻的一端分别与其他电阻的一端用一根导线连接，最后将每个电阻的另一端与直流电源的负极用一根导线连接。

用万用表测量并记录电路中的总电流和总电压。

4. 分析实验结果：根据实验数据计算出串联电路中每个电阻的电压和电流值，以及并联电路中总电压和电流值。

比较串联和并联电路中的电流和电压数值，可以发现串联电路中总电阻较大，电流在各个电阻间分配；而并联电路中总电阻较小，电流在各个电阻上相等。

二、实验装置实验装置包括直流电源、电阻箱、万用表和导线等。

1. 直流电源：提供实验所需的电压，可以通过调节电压大小来改变电路中的总电压。

直流电源应稳定可靠，电压调节范围适宜。

2. 电阻箱：用于串联和并联实验中的电阻值调节。

电阻箱应具有较高的精度和稳定性，可调节的电阻值应覆盖实验需要。

3. 万用表：用于测量电阻、电流和电压等。

万用表应具备较高的测量精度和灵敏度，且操作简便。

4. 导线：连接电路中各个元件。

导线应具备较低的电阻和较好的导电性能，同时也要具备足够的强度和耐久性。

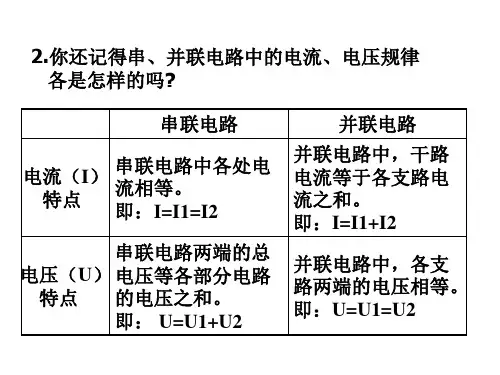
知识点一:；:电阻的串联有以下几个特点：（指R1、R2 串联，串得越多，总电阻越大）①电流：I=I 1=I2（串联电路中各处的电流相等）②电压：U=U 1+U2（串联电路中总电压等于各部分电路电压之和）③电阻：R=R1+R2（串联电路中总电阻等于各串联电阻之和）；如果n 个等值电阻（R）串联,则有R 总=nR注：总电阻比任何一个分电阻都大，其原因是电阻串联相当于增加了导体的长度；④分压作用：U1/U 2=R 1/R 2（阻值越大的电阻分得电压越多，反之分得电压越少）⑤比例关系：电流：I1∶I2=1∶1例题：电阻为12Ω的电铃正常工作时的电压为 6 V ，若把它接在8 V 的电路上，需要给它串联一个多大的电阻?（要求画出电路图，在图上标出有关物理量）例题：把电阻R1=20Ω与电阻R2=15Ω串联起来接入电路中，流过R1、R2的电流之比是，R1、R2两端的电压之比是_______________________ 。

例题：如图所示，电源电压为10V，闭合开关S后，电流表、电压表的示数分别为O.5A和6V。

求：（1）通过R1的电流I1是多少?（2）马平同学在求R2的电阻值时，解题过程如下：根据欧姆定律：R2=U/I=6V/0.5A=12 Ω请你指出马平同学在解题过程中存在的错误，并写出正确的解题过程。

练习1．电阻R1和R2串联后接在电压为 6 V 的电源上，电阻R1=2Ω，R2=4Ω，求：（1）总电阻．（2）R 1两端的电压．（要求画出电路图，在图上标出有关物理量）2．如图所示的电路中，若电源电压保持 6 V 不变，电阻R1=10Ω，滑动变阻器R2的变化范围是O～20Ω．求：（1）欲使电压表的示数为 4 V，则此时电流表的示数为多大?滑动变阻器连入电路的电阻是多大?（2）当滑动变阻器连人电路的电阻为20Ω时，电流表、电压表的示数分别是多大?电阻的串联和并联3．把电阻R1=5Ω与电阻R2=15Ω串联起来接入电路中，流过R1、R2的电流之比是______R 1、R 2两端的电压之比是知识点二；.电阻的并联有以下几个特点： （指 R 1、R 2 并联，并得越多，总电阻越小 ）①电流：I=I 1+I 2（干路电流等于各支路电流之和 ） U=U 1=U 2（干路电压等于各支路电压 ） 1/R=1/R 1＋ 1/R 2 （总电阻的倒数等于各支路电阻的倒数之和 ）； 注：总电阻比任何一个分电阻都小，其原因是电阻并联相当于增加了导体的横截面积；②电压：③电阻：变形式 R=R 1.R 2/（R 1＋R 2）此变形式只适用于两个电阻并联的情况，多于两个电阻并联 则不适用。