第三章阻抗的串联与并联

实验九 阻抗的串联、并联和混联一、实验目的（1）研究阻抗的串联、并联和混联的特点。

（2）加深对复阻抗、阻抗角、相位差等概念的理解。

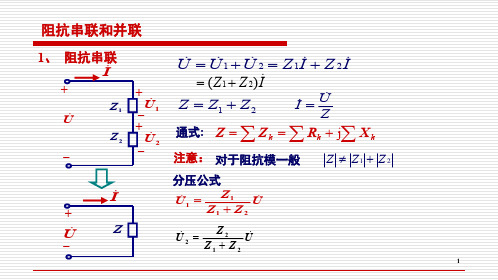
二、实验原理1．阻抗的串联两个元件串联后的总阻抗为两个元件的复阻抗之和：12Z Z Z =+总2．阻抗的并联两个元件并联后的总导纳为两个元件的导纳之和：12Y Y Y =+总3．阻抗的混联两个元件先并联，再与第三个元件串联，混联电路总的阻抗：()12123312//Z Z Z Z Z Z Z Z Z =+=++总4.测量阻抗的方法测量阻抗除用三表法外，还可以用示波器法，即用双踪示波器测量电压与电流的相位差，加上用电压表、电流表测量元件两端的电压和流过的电流，就可以计算出元件的阻抗。

测量元件的电压与电流的相位差，示波器接法如图9-1所示。

其中通道A 接电路的输入端，显示的是电压信号，示波器不能直接测量电流信号，需要在电路中串联一小电阻r ，将流过电阻r 的电流转化为电压信号，示波器的通道B 接电阻r 的两端，因为电阻两端的电压与流过的电流是同相的，所以通道A 和通道B 的相位差就是电压与电流的相位差。

电压与电流的相位关系如图9-2所示，可以看到，电压信号超前电流信号，元件为感性，否则元件为容性。

电压与电流的相位差为：360360tt f Tj D D =窗=D 创则元件的阻抗为：cos sin U Z Z j Z Ij j j =?图9-1 测量元件的电压与电流的相位差三、实验仪器与设备（1）交流电压表、交流电流表、双踪示波器和功率表各1台。

（2）元件：电阻（20W ，2mH ）1个，电感线圈（25mH ，3W ）1个，电容（100uF,1W ）1个。

（3）可调交流电源1台。

四、实验内容1．用示波器法测量电阻与电感线圈串联的阻抗Z 总，并把实验数据记录在表9-1中。

验证12Z Z Z =+总是否成立。

2. 用三表法测量电阻与电感线圈并联的总导纳Y 总，自行设计电路图，并把实验数据记录在表9-2中，验证12Y Y Y=+总是否成立。

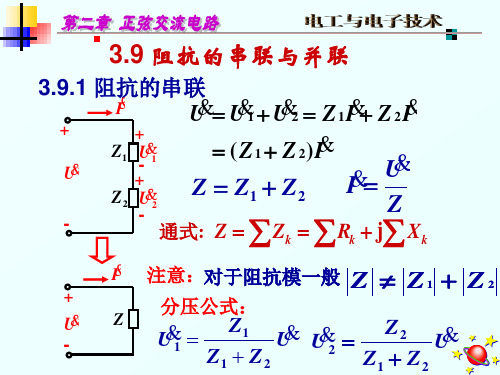
单元电路的网络参量，可以直接根据未归一化网络参量的 定义求得。

也可以根据网络参量间的互换关系，由另一组网络参量转推得到。

一、串联阻抗图 1 串联阻抗由图 1，根据基尔霍夫定律，有：12121I I U U ZI =-⎧⎨=+⎩ (1-1) 1.1 Y 矩阵根据导纳矩阵定义：11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (1.1-1)将式（1-1）代入，有2111011U I Y U Z ===，1112021U I Y U Z ===-，2221011U I Y U Z===-，1222021U I Y U Z===则[]11122122111=11Y Y Y Y Y Z -⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦(1.1-2)1.2 A 矩阵根据转移矩阵定义：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (1.2-1)将式（1-1）代入，有2111021I U A U ===，211202-U U A Z I ===，2121020I I A U ===，2122021U I A I ===-则[]111221221=01A A Z A A A ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (1.2-2)1.3 S矩阵根据S矩阵和a矩阵的转换关系：[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS S a a a aa a a aZZ ZZZR ZR Z Z R+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤+-=⎢⎥++-+⎢⎥⎣⎦(1.3-1)考虑Z01=Z02情况，此时R=1，则[]2122ZSZ Z⎡⎤=⎢⎥+⎢⎥⎣⎦(1.3-2) 1.4 T矩阵根据S矩阵和T矩阵的转换关系：[]2211212111111(1)(1)41(1)1111STS SSZ RZ R ZR Z R Z Z R RR Z R ZR Z R ZR Z R Z-⎡⎤=⎢⎥-⎣⎦⎡⎤-+-⎢⎥++⎥=⎥+--+--++⎥++++⎢⎥⎣⎦⎡⎤++--=⎥+--+⎥⎦(1.4-1)考虑Z01=Z02情况，此时R=1，则[]2122Z ZTZ Z⎡⎤+-=⎢⎥-⎢⎥⎣⎦(1.4-2)二、并联导纳图 2 并联导纳由图 2，根据基尔霍夫定律，有：12121U U I I YU =⎧⎨+=⎩ (2-1) 2.1 Z 矩阵根据阻抗矩阵定义，有：11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (2.1-1) 将式（2-1）代入，有2111011I U Z I Y===，1112021I U Z I Y ===，2221011I U Z I Y ===，1222021I U Z I Y===(2.1-2)即[]1112212211111ZZ Z Z Z Y ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦(2.1-3)2.2 A 矩阵根据转移矩阵定义：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (2.2-1)将式（1-1）代入，有2111021I U A U ===，2112020-U U A I ===，212102I I A Y U ===，2122021U I A I ===-则[]1112212210=1AA A A A Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (2.2-2)2.3 S矩阵根据S矩阵和a矩阵的转换关系：[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS Sa a a aa a a aYRYRR YRR YR R YR+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤--=⎢++--⎢⎣⎦⎥⎥(2.3-1)考虑Y01=Y02情况，此时R=1，则[]2122YSY Y⎡⎤-=⎢⎥+-⎢⎥⎣⎦(2.3-2) 2.4 T矩阵根据S矩阵和T矩阵的转换关系：[]2211212111111(1)(1)41(1)1111STS SSYR RYR R YRR YR R YR YR R RR YR R YRR YR R YRR YR R YR-⎡⎤=⎢⎥-⎣⎦⎡⎤+-⎢⎥++⎥=⎥------+--⎢⎥++++⎢⎥⎣⎦⎡⎤+++-=⎥---+⎥⎦(2.4-1)考虑Y01=Y02情况，此时R=1，则[]2122Y YTY Y⎡⎤+=⎢⎥--⎢⎥⎣⎦(2.4-2)三、无耗传输线段图 3 无耗传输线段根据传输线方程的解：00()cos sin ()cos sin L L L L U z U z jI Z z U I z I z j z Z ββββ=+⎧⎪⎨=+⎪⎩(3-1)根据传输线方程的关系，22,,L L z U U I I θβ===-，则12202120cos sin sin cos U U jI Z U I j I Z θθθθ=-⎧⎪⎨=-⎪⎩(3-2) 3.1 Z 矩阵根据阻抗矩阵定义，有：11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (3.1-1)将式（3-2）代入有：212110021cos cot sin I U U Z jZ U I j Z θθθ====- (3.1-2)11120csc I U Z jZ I θ===- (3.1-3)2221001csc I U Z jZI θ===-(3.1-6) 1222002cot I U Z jZ I θ===- (3.1-7)即[]001112002122cot csc csc cot jZ jZ ZZ Z jZ jZ Z Z θθθθ--⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦(3.1-8)3.2 Y 矩阵根据导纳矩阵定义：11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (3.2-1)将式（3-2）代入，根据定义，U 2=0时，将式（3-2）两式相除，有2121101200cos 1cot sin U I I Y j U jI Z Z θθθ====- (3.2-2)根据定义，U 1=0时，由式（3-2_1）有22200cos 1cot sin U I j j U Z Z θθθ=-=-，代入式（3-2_2）有221200011sin (cot )cos sin U U I j j U j Z Z Z θθθθ=--=，进而1112021csc U I Y jU Z θ=== (3.2-3) 根据定义，U 2=0时，由式（3-2_1）有 2221011csc U I Y jU Z θ=== (3.2-4) 根据定义，U 1=0时，由式（3-2_1）有12220200cos 1cot sin U I Y j U jZ Z θθθ====- (3.2-5)由式（3.2-2）-式（3.2-5）有：[]00111221220011cot csc =11csc cot j j Z Z Y Y Y Y Y j j Z Zθθθθ⎡⎤-⎢⎥⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦-⎢⎥(3.2-6)将式（3.1-8）和式（3.2-6）相乘，有 [][]00000000222211cot csc cot csc csc cot 11csc cot 10csc cot 0010csc cot j jZ Z jZ jZ Z Y jZ jZ j j Z Z θθθθθθθθθθθθ⎡⎤-⎢⎥--⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦-⎢⎥⎣⎦⎡⎤-⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦ (3.2-14)根据式（3-2）以及A 矩阵定义，有211102cos I U A U θ===，2112002sin -U U A jZ I θ===，21210201sin I I A jU Z θ===，212202cos U I A I θ===-。

串联谐振电路和并联谐振电路的阻抗在电路的世界里，串联谐振电路和并联谐振电路就像是一对欢喜冤家，各自有各自的特点和魅力。

想象一下，串联谐振电路就像是一条紧紧相连的链子，每个链接都相互依赖，缺一不可。

电流像水流一样，从一个元件流向另一个元件，电感和电容在这条链子上舞动着，互相配合。

当频率达到某个特定值时，电路的阻抗会达到最低点，电流如同洪水猛兽，尽情地奔腾而过，这就是我们说的谐振。

简直就像一场音乐会，所有乐器合奏得天衣无缝，观众们都陶醉其中。

而说到并联谐振电路，哦，这就像是一场派对，大家各自为政，想怎么玩就怎么玩。

电流在不同的路径上分流，各个元件各自独立，互不干扰。

每当频率合适时，这些独立的元件又齐心协力，产生最低的阻抗，真是热闹非凡，电流像开了挂一样，欢快地在每个支路上游荡。

想想那些独立的乐手，各自弹奏着不同的旋律，但一旦达到和谐的时刻，整个乐队瞬间凝聚成一体，效果真是令人惊艳。

你可能会问，这两者之间有什么区别呢？串联谐振电路的阻抗是由电感和电容的相互作用决定的。

电感像个调皮的小孩，抵抗变化的电流；而电容则像个爱捣乱的朋友，存储能量，随时准备释放。

它们之间的斗智斗勇，构成了串联谐振的精彩部分。

此时，阻抗达到最小，电流流动畅通无阻，这种感觉就像是在拥挤的地铁里突然找到一处空间，舒舒服服地松了一口气。

而并联谐振电路的阻抗就更有意思了。

这种电路的总阻抗是由各个支路的阻抗并行组合而成的，真是让人目不暇接。

电流在每条支路上分流，各自的阻抗犹如一场无形的较量，最终形成一个最低的总阻抗。

这就像在马拉松比赛中，选手们各自发挥，谁也不甘示弱，最后却在终点线前形成了惊人的协作，仿佛共同打破了时间的桎梏。

生活中这些电路又能给我们带来什么启示呢？串联和并联就像生活中的合作与独立。

有时候我们需要团结一心，像串联电路一样，大家齐心协力，才能战胜困难；而我们又要学会独立，像并联电路一样，各自发挥所长，成就自己的目标。

这样的道理，简直是电路给我们的生活上了一课。

实验三 单相交流串联电路一、实验目的1．研究交流串联电路中电压、电流的相位关系，观察电容、电感元件上电压与电流的相位关系。

2．测绘RLC串联电路的频率特性曲线，进一步理解RLC串联电路谐振时的特征。

二、实验表格及数据谐振时的电路参数RLC串联电路的幅频特性1．复习函数发生器及示波器的使用方法。

2．阅读实验指导书，弄清RLC交流串联电路的特性。

了解电路参数对谐振曲线形状及谐振频率的影响。

3. 计算L=35mH和L=30mH时图3.1实验电路的谐振频率f01= 4240Hz、f02= 3926Hz。

4．在RLC串联电路中，当电源频率f =（3926Hz）时，电路发生串联谐振，此时电路的端电压与电流的相位 相同 ，电路呈 阻 性（阻、感、容）。

5. 思考题（1）为保证电源端电压为250mV ，在调节函数发生器的输出幅度旋钮AMPL 时，函数发生器是否接入实验电路？答：接入。

（2）在实验线路图3.2中，元件按CLR 排列顺序。

若按照CRL 排列顺序，还能用示波器观测总电压和电流的相位关系吗？四、实验报告要求1．整理测量数据，将计算值填入表中。

2．在座标纸上绘出RLC 串联电路的幅频特性曲线I=F ( f )。

R =51Ω和R =100Ω的两条曲线画在同一坐标内，注明谐振频率数值及每条曲线的Q 值并在曲线上标出谐振回路的通频带。

3.用测量值计算谐振回路的品质因数Q 。

并分析电阻R 对Q 值、选择性及通频带的影响。

答：利用公式，可得51Q =25.053.2=10.2；100Q =25.064.1=6.56。

电阻R 越大，会使得在电容或电感上的电压相对的减少，从而使得Q 变的小了，由频率特性曲线可知，Q 越大，曲线越尖锐，即选择性越强，通频带越窄。

4．实验表明，当f < f o 时，电压在相位上 滞后 电流，电路呈 容 性。

当f >f o 时，电压在相位上 超前 电流，电路呈 感 性。