当前位置：文档之家 › 阻抗的串联与并联

阻抗的串联与并联

  • 格式：ppt
  • 大小：707.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

阻抗的串联与并联课件-精选文档

阻抗的串联与并联课件-精选文档

注意:对于阻抗模一般 分压公式：
ZZ 1 Z 2
+ U
Z
2019/3/14
Z Z 2 1 U U U U 2 1 Z Z 1 Z 2 1 Z 2
2
2.5 阻抗的串联与并联
例1: 有两个阻抗Z Z 2.5 j4 Ω , 它们 6.16 j9 Ω , 2 1 ， 和 U U 串联接在 U 的电源; 求: I 220 30 V 1 2 I 并作相量图。 + + 解： Z Z Z (6.16 2.5) j(9 4) 1 2 Z1 U 1 8.66 j5 10 30 Ω
Z1
-
I 1
Z2
X 1 R XL C 1 Y j( ) 1 2 2 2 Z Z Z Z 1 1 1 1
I 2
j1 G j( B B ) Y e 1 L 1 C1 1
B B L 1 1 1 arctan C G 1
1 j 2 Y G j( B B ) Y e 同理： 2 2 L 2 C 2 2 Z 2
I
+
Z1 Z2 Z Z1 Z2
U
Z
-
1 1 1 注意：对于阻抗模一般 Z Z1 Z2
1 1 通式: Z Zk
分流公式：I 1
2019/3/14
Z Z 1 2 I I I2 Z Z 1 Z 2 1 Z 2
6
+
,Z , 3 j4 Ω 8 j6 Ω 例2: 有两个阻抗 Z 1 2 、 220 它们并联接在 U 的电源上; 求: I I 0 V 1 2 并作相量图。 和 I Z 5 53 10 37 1Z 2 解: Z I Z1 Z2 3 j48 j6

简述串联电抗器和并联电抗器的作用

简述串联电抗器和并联电抗器的作用

简述串联电抗器和并联电抗器的作用
串联电抗器通常用于限制合闸涌流和抑制高次谐波，它可以与电容器组或密集型电容器串联，限制电容器的合闸涌流，同时也能削减不装设串联电抗器时电力电抗器组对系统谐波的放大作用。

并联电抗器则主要用于改善电力系统的稳定性，降低电力损耗。

它可以补偿电源端的电感，减小线路阻抗，提高电源质量，同时改善负载侧的功率因数，降低线路和设备的损耗，提高能源利用效率。

以上信息仅供参考，如有需要，建议咨询专业技术人员。

阻抗的串联与并联

阻抗的串联与并联

U 1
Z1 Z1 Z2
U
6.16 j9 22030 239.855.6V
8.66 j5
U 1
55.6 30
相量图
UU5 82 I
U 2
Z2 Z1 Z2
U
2.5 j4 8.66 j5
22030
103.6 58V
注意 U U 1 U 2 U U 1 U 2
阻抗串联与并联
U
II试2 求：（I11）电路解中：（各Z1电）1 流设；RU（2j）1画L0出相0量oV图。jL j2 53103 18106 2 j2 53103 18106
I2 I
74.5o 71.6o
U
I1
（2）相量图
2 j6 6.3271.6o
I1
U Z1
10 0o 6.3271.6o
1.58 71.6o 0.5 j1.5A
Z2
1 jC
1 j2 53103 1106
ห้องสมุดไป่ตู้
j3 3 90o
II2I1ZU2
10 0o 3.3 90o 3 90o
I2 (0.5 j1.5) j3
j3.3A
0.5 j1.8 1.87 74.5o A
阻抗串联和并联
1、
阻抗串联 I
+
U
Z1
Z2
_
+_U 1 +_U 2
U
U (Z
1 U 1 Z 2)
2I
Z 1I
Z 2I
Z Z1 Z2
I U Z
通式: Z Zk Rk j X k
注意： 对于阻抗模一般 Z Z1 Z 2
I +
分压公式

阻抗的串联与并联

阻抗的串联与并联

△ ω = ( ω 2- ω 1)
值,对其它频率不会产生这样的结果.因此该电路具 对其它频率不会产生这样的结果. 选频作用.常用于正弦波振荡器. 有选频作用.常用于正弦波振荡器.
1 同相, 仅当 ω = ω0 = RC 时,1与 U2同相,U2=U1/3 为最大 U
3.10.2 串联谐振
谐振的概念: 谐振的概念: 在同时含有L 的交流电路中, 在同时含有 和C 的交流电路中,如果总电压和 总电流同相,称电路处于谐振状态. 总电流同相,称电路处于谐振状态.此时电路与电 源之间不再有能量的交换,电路呈电阻性. 源之间不再有能量的交换,电路呈电阻性. 串联谐振:L 与 C 串联时 u,i 同相 串联谐振: 并联谐振: 并联谐振:L 与 C 并联时 u,i 同相 研究谐振的目的, 研究谐振的目的,就是一方面在生产上充分利 用谐振的特点, 如在无线电工程 如在无线电工程, 用谐振的特点,(如在无线电工程,电子测量技术等 许多电路中应用). 许多电路中应用 .另一方面又要预防它所产生的危 害.
3.8 阻抗的串联与并联 3.8.1阻抗的串联 3.8.1阻抗的串联 I U = U 1 + U 2 = Z 1I + Z 2 I + + Z1 U1 = ( Z 1 + Z 2) I
U
+ Z2 U2
-
Z = Z1 + Z2
通式: 通式 Z =
k
I
∑Z = ∑R + j∑X
k
U I= Z
=
1 1 3 + j( ω R C ) ω RC
频率特性
T (j ω ) =
1 ω 1 ω 3 + j( ω R C ) 3 + j( 0) ω RC ω ω 0 ω ω 0 ω ω 1 0 = arctan 3 2 ω0 2 ω 3 + ω ω 0 =

第8讲RLC串联电路及阻抗串并联

第8讲RLC串联电路及阻抗串并联
方法2：复数运算 解： U 220 20V
220 20 U I A 4.4 73A Z 50 - 53 I R 4.4 73 30V 132 73V U R jI X j4.4 40 73V 176 163V U L L jI X j4.4 80 73V 352 - 17V U C C
Z R 2 ( X L X C ) 2 30 2 (40 80) 2 50 Ω ,
方法1： U 220 (1) I A 4.4A
因为 ψ u ψ i -53, 所以ψi 73
50 X L XC 40 - 80 arctan arctan -53 R 30
239.8 55.6 V Z I (2.5 j4) 22V 103.6 58V 同理： U 2 2
或利用分压公式：
I
+
U
Z1 U 1
Z1 6.16 j9 U1 U 220 30 V + Z Z 8.66 j5 1 2
电路参数与电路性质的关系：
当 XL >XC 时， > 0 ，u 超前 i 当 XL < XC 时 ， < 0 ， u 滞后 i 当 XL = XC 时 ， = 0 ， u. i 同相 呈感性 呈容性 呈电阻性
2) 相量图
+
R
I
参考相量
U
jXL
_ -jXC
U L + U L U U U U R I _R U L C + X < X L C XL > XC UL U U _ L C U U I R + ( > 0 感性) U ( < 0 容性) C U U C _ C

5第一节 复阻抗的串联与并联

5第一节 复阻抗的串联与并联
第5章正弦交流电路的相量分析法
第一节复阻抗的串联与并联
1.阻抗的串联及并联
1）下图给出了多个复阻抗（每个复阻抗都由R、L、C组合而成）串联的电路,电流和电压的参考方向如图中所示。
由KVL可得
其中Z为串联电路的等效阻抗,由上式可得
Z=Z1+Z2+…+Zn
即串联电路的等效复阻抗等于各串联复阻抗之和
2）阻抗并联
上式就是由复阻抗等效为复导纳的参数条件。
2）将复导纳等效为复阻抗
图5.25复阻抗与复导纳的等效变换
例已知加在电路上的端电压为u=311sin(ωt+60°)V,通过电路中的电流为。求|Z|、阻抗角φ和导纳角φ′。
解电压的相量为
所以
多阻抗并联
2.无源二端网络的等效电路
无源二端网络总可以用一个等效复阻抗或等效复导纳来表示。
正弦交流电路的复阻抗Z称为电路的阻抗Z是一个复数,所以又称为复阻抗, |Z|是阻抗的模,φ为阻抗角。复阻抗的图形符号与电阻的图形符号相似。复阻抗的单位为Ω。
3.等效复阻抗及复导纳的相互转换
1）将复阻抗等效为复导纳

实验九 阻抗的串联、并联和混联(共3页)

实验九 阻抗的串联、并联和混联一、实验目的（1）研究阻抗的串联、并联和混联的特点。

（2）加深对复阻抗、阻抗角、相位差等概念的理解。

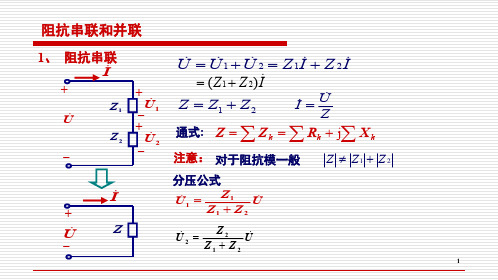
二、实验原理1．阻抗的串联两个元件串联后的总阻抗为两个元件的复阻抗之和：12Z Z Z =+总2．阻抗的并联两个元件并联后的总导纳为两个元件的导纳之和：12Y Y Y =+总3．阻抗的混联两个元件先并联，再与第三个元件串联，混联电路总的阻抗：()12123312//Z Z Z Z Z Z Z Z Z =+=++总4.测量阻抗的方法测量阻抗除用三表法外，还可以用示波器法，即用双踪示波器测量电压与电流的相位差，加上用电压表、电流表测量元件两端的电压和流过的电流，就可以计算出元件的阻抗。

测量元件的电压与电流的相位差，示波器接法如图9-1所示。

其中通道A 接电路的输入端，显示的是电压信号，示波器不能直接测量电流信号，需要在电路中串联一小电阻r ，将流过电阻r 的电流转化为电压信号，示波器的通道B 接电阻r 的两端，因为电阻两端的电压与流过的电流是同相的，所以通道A 和通道B 的相位差就是电压与电流的相位差。

电压与电流的相位关系如图9-2所示，可以看到，电压信号超前电流信号，元件为感性，否则元件为容性。

电压与电流的相位差为：360360tt f Tj D D =窗=D 创则元件的阻抗为：cos sin U Z Z j Z Ij j j =?图9-1 测量元件的电压与电流的相位差三、实验仪器与设备（1）交流电压表、交流电流表、双踪示波器和功率表各1台。

（2）元件：电阻（20W ，2mH ）1个，电感线圈（25mH ，3W ）1个，电容（100uF,1W ）1个。

（3）可调交流电源1台。

四、实验内容1．用示波器法测量电阻与电感线圈串联的阻抗Z 总，并把实验数据记录在表9-1中。

验证12Z Z Z =+总是否成立。

2. 用三表法测量电阻与电感线圈并联的总导纳Y 总，自行设计电路图，并把实验数据记录在表9-2中，验证12Y Y Y=+总是否成立。

第三章阻抗的串联与并联


§3-9 复杂交流电路的分析计算
与第二章所讨论复杂直流电路一样，复杂交流电 路也要应用第二章所介绍的方法进行分析计算。 所不同的是：电压和电流应以相量来表示；电路 中的R、L、C要用相应的复数阻抗或复数导纳来 表示。由此，等效法及叠加法等方法都适用。 分析复杂交流电路的基 U Z I 本依据仍然是欧姆定律 及克希荷夫定律，但须 ( I ) 0 用其相量形式。 以下结合例题来分析复 ( U) 0 杂交流电路。
IS
I

+
-
US

I

Z1
Z2
Z123
+ Z 3 -
Z
IS

Z3
Z12
Z
I

US

Z
I

Z12
例 题
解：
电路如图所示，已知R=R1=R2=10Ω， L=31.8mH，C=318μF，f=50Hz，U=10V， 试求（1）并联支路端电压Uab； （2）求P、Q、S及COS
XL=2πfL
=10Ω
+
u

U

I R 1
jXL

R2 -jXC

I1

I2
U 220 o I 49.2 / 26.5 A o Z 4.47 / 26.5
例 题 分 析

I1 44/ 53o A I 2 22/ 37 A
o

U

I R 1
jXL

R2 -jXC

I 49.2/ 26.5o A
1 ) RC
二. 串联谐振
• 在具有电感和电容元件的电路中，电路两端的 电压与其中的电流一般是相位不同的。如果调 节电路的参数或调节电源的频率而使两者相位 相同，电路中就会发生谐振现象。 • 谐振可分为串联谐振和并联谐振两种情况。 在R、L、C元件的串联电路中， i 当 XL XC 或 2fL 1 2fC 则 arctg X L XC 0 R 即电压 u 与电流 i 同相，这 时电路发生了串联谐振。 R

阻抗的串联与并联


+
Z1 Z 2 5 53 10 37 解: Z I Z1 Z 2 3 j4 8 j6
I1
Z2
U -
Z1
I2
50 16 4.47 26.5Ω 11.8 10.5
U 220 0 I1 A 44 53 A Z1 5 53 U 220 0 同理： 2 I A 22 37 A Z 2 10 37
例4: 图示电路中已知: u 220 2 sin314t V i1 22sin(314 45) A i2 11 2 sin(314t 90) A t 试求: 各表读数及参数 R、L 和 C。 i 解：求各表读数
A
(1)复数计算
+
U 220 V 22 I1 15.6 A 2 I 2 11 A
U 220 0 Z1 14.1 45 10 j10 Ω I1 15.6 45 XL 0.0318H R X L 10Ω L 2π f
U 220 0 Z2 20 90 Ω 所以X C 20 Ω I 2 11 90 1 1 C 159 μ F 2 π f X C 314 20 Z 方法2： XL U Z1 14.1Ω 45 I1 R R Z cos45 10 Ω
-
+ Z2 U 2
239.8 55.6 V
-
- U2
U1
Z2 2.5 j4 220 30V U Z1 Z 2 8.66 j5 103.6 58V
58 U2 U
I
相量图
55.6
注意： U U 1 U 2

单元电路(串联阻抗、并联导纳、无耗传输线)的基本网络参量(Z矩阵、Y矩阵、A矩阵、S矩阵、T巨矩阵)

单元电路的网络参量，可以直接根据未归一化网络参量的 定义求得。

也可以根据网络参量间的互换关系，由另一组网络参量转推得到。

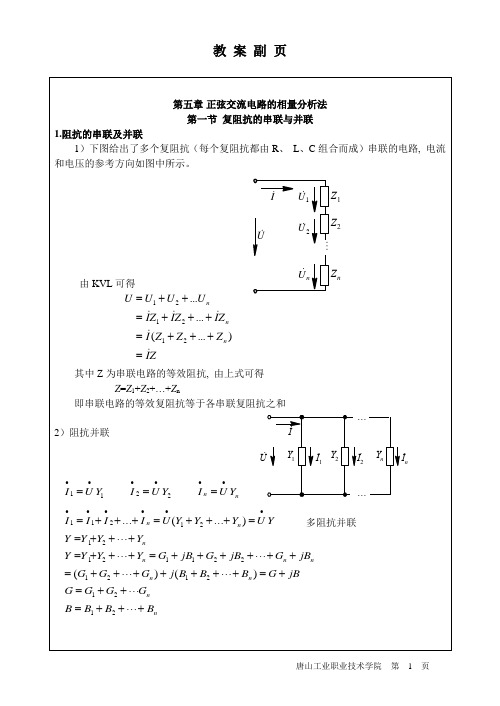
一、串联阻抗图 1 串联阻抗由图 1，根据基尔霍夫定律，有：12121I I U U ZI =-⎧⎨=+⎩ (1-1) 1.1 Y 矩阵根据导纳矩阵定义：11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (1.1-1)将式（1-1）代入，有2111011U I Y U Z ===，1112021U I Y U Z ===-，2221011U I Y U Z===-，1222021U I Y U Z===则[]11122122111=11Y Y Y Y Y Z -⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦(1.1-2)1.2 A 矩阵根据转移矩阵定义：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (1.2-1)将式（1-1）代入，有2111021I U A U ===，211202-U U A Z I ===，2121020I I A U ===，2122021U I A I ===-则[]111221221=01A A Z A A A ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (1.2-2)1.3 S矩阵根据S矩阵和a矩阵的转换关系：[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS S a a a aa a a aZZ ZZZR ZR Z Z R+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤+-=⎢⎥++-+⎢⎥⎣⎦(1.3-1)考虑Z01=Z02情况，此时R=1，则[]2122ZSZ Z⎡⎤=⎢⎥+⎢⎥⎣⎦(1.3-2) 1.4 T矩阵根据S矩阵和T矩阵的转换关系：[]2211212111111(1)(1)41(1)1111STS SSZ RZ R ZR Z R Z Z R RR Z R ZR Z R ZR Z R Z-⎡⎤=⎢⎥-⎣⎦⎡⎤-+-⎢⎥++⎥=⎥+--+--++⎥++++⎢⎥⎣⎦⎡⎤++--=⎥+--+⎥⎦(1.4-1)考虑Z01=Z02情况，此时R=1，则[]2122Z ZTZ Z⎡⎤+-=⎢⎥-⎢⎥⎣⎦(1.4-2)二、并联导纳图 2 并联导纳由图 2，根据基尔霍夫定律，有：12121U U I I YU =⎧⎨+=⎩ (2-1) 2.1 Z 矩阵根据阻抗矩阵定义，有：11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (2.1-1) 将式（2-1）代入，有2111011I U Z I Y===，1112021I U Z I Y ===，2221011I U Z I Y ===，1222021I U Z I Y===(2.1-2)即[]1112212211111ZZ Z Z Z Y ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦(2.1-3)2.2 A 矩阵根据转移矩阵定义：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (2.2-1)将式（1-1）代入，有2111021I U A U ===，2112020-U U A I ===，212102I I A Y U ===，2122021U I A I ===-则[]1112212210=1AA A A A Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (2.2-2)2.3 S矩阵根据S矩阵和a矩阵的转换关系：[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS Sa a a aa a a aYRYRR YRR YR R YR+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤--=⎢++--⎢⎣⎦⎥⎥(2.3-1)考虑Y01=Y02情况，此时R=1，则[]2122YSY Y⎡⎤-=⎢⎥+-⎢⎥⎣⎦(2.3-2) 2.4 T矩阵根据S矩阵和T矩阵的转换关系：[]2211212111111(1)(1)41(1)1111STS SSYR RYR R YRR YR R YR YR R RR YR R YRR YR R YRR YR R YR-⎡⎤=⎢⎥-⎣⎦⎡⎤+-⎢⎥++⎥=⎥------+--⎢⎥++++⎢⎥⎣⎦⎡⎤+++-=⎥---+⎥⎦(2.4-1)考虑Y01=Y02情况，此时R=1，则[]2122Y YTY Y⎡⎤+=⎢⎥--⎢⎥⎣⎦(2.4-2)三、无耗传输线段图 3 无耗传输线段根据传输线方程的解：00()cos sin ()cos sin L L L L U z U z jI Z z U I z I z j z Z ββββ=+⎧⎪⎨=+⎪⎩(3-1)根据传输线方程的关系，22,,L L z U U I I θβ===-，则12202120cos sin sin cos U U jI Z U I j I Z θθθθ=-⎧⎪⎨=-⎪⎩(3-2) 3.1 Z 矩阵根据阻抗矩阵定义，有：11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (3.1-1)将式（3-2）代入有：212110021cos cot sin I U U Z jZ U I j Z θθθ====- (3.1-2)11120csc I U Z jZ I θ===- (3.1-3)2221001csc I U Z jZI θ===-(3.1-6) 1222002cot I U Z jZ I θ===- (3.1-7)即[]001112002122cot csc csc cot jZ jZ ZZ Z jZ jZ Z Z θθθθ--⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦(3.1-8)3.2 Y 矩阵根据导纳矩阵定义：11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (3.2-1)将式（3-2）代入，根据定义，U 2=0时，将式（3-2）两式相除，有2121101200cos 1cot sin U I I Y j U jI Z Z θθθ====- (3.2-2)根据定义，U 1=0时，由式（3-2_1）有22200cos 1cot sin U I j j U Z Z θθθ=-=-，代入式（3-2_2）有221200011sin (cot )cos sin U U I j j U j Z Z Z θθθθ=--=，进而1112021csc U I Y jU Z θ=== (3.2-3) 根据定义，U 2=0时，由式（3-2_1）有 2221011csc U I Y jU Z θ=== (3.2-4) 根据定义，U 1=0时，由式（3-2_1）有12220200cos 1cot sin U I Y j U jZ Z θθθ====- (3.2-5)由式（3.2-2）-式（3.2-5）有：[]00111221220011cot csc =11csc cot j j Z Z Y Y Y Y Y j j Z Zθθθθ⎡⎤-⎢⎥⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦-⎢⎥(3.2-6)将式（3.1-8）和式（3.2-6）相乘，有 [][]00000000222211cot csc cot csc csc cot 11csc cot 10csc cot 0010csc cot j jZ Z jZ jZ Z Y jZ jZ j j Z Z θθθθθθθθθθθθ⎡⎤-⎢⎥--⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦-⎢⎥⎣⎦⎡⎤-⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦ (3.2-14)根据式（3-2）以及A 矩阵定义，有211102cos I U A U θ===，2112002sin -U U A jZ I θ===，21210201sin I I A jU Z θ===，212202cos U I A I θ===-。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则：I2 [100 /(5 j5)]A 10 2 45A
I1 10 90A j10 A I I1 I2 10 0 A 所以A读数为 10安
j10Ω I
A
I1
A I2 C1
B
5Ω j5Ω V
已知：I1=10A、 UAB =100V，
求：A、V 的读数
因为 I I1 I2 10 0 A 所以U L I ( j10 )V j100 V
+ 3
U
4 _
V1 6V V2 8V
+ 6
U
8
_
V1 30V V2 40V
(a)
(b)
Z 7Ω U=14V ? Z 10Ω U=70V ?
两个阻抗串联时,在什么情况下:
Z Z1 Z2 成立。
2.5.2 阻抗并联
I +
U
-
Z1 I1Z2 I2
I I1 I U
Z Z
I2
U Z1
11
Z Z1
一般用相量式计算:
(1) Z1 、Z2 Z I i
(2) I I1、I2 i1 ,i2
解：用相量式计算
I
U 220 0 V
+ 50Ω 100Ω
Z1 R 1 j X L (100 j1200) Ω
Z2 jXC j 140 Ω
U j200Ω I1 I2 - j400Ω
-
Z [50 (100 j200) (j400)] (50 320 j240) 440 33Ω 100 j200 j400
3.9 阻抗的串联与并联
3.9.1 阻抗的串联
I
U U 1 U 2 Z1I Z 2I
+ U
-
+
Z1 -U1
+
Z2
U
-
2
(Z1 Z 2)I
Z Z1 Z2
I U Z
通式: Z Zk Rk j Xk
I 注意：对于阻抗模一般 Z Z 1 Z 2
+
分压公式：
U
-
Z
U 1
Z1 Z1 Z2
-
I2 - j400Ω
0.5 93.8A
所以 i 0.5 2 sin (ωt 33)A
i1 0.89 2 sin (ωt 59.6)A i2 0.5 2 sin (ωt 93.8)A
例2： 下图电路中已知：I1=10A、UAB =100V，
求：总电压表和总电流表 的读数。
j10Ω I
Z 2Ω I=8A ?
两个阻抗并联时,在什么情况下:
1 1 1 成立。
Z Z1 Z2
1. 图示电路中,已知 X L XC R 2Ω
电流表A1的读数为3A,
试问(1)A2和A3的读数为多少? + A1 A2 A3 (2)并联等效阻抗Z为多少? U L R C -

2. 图示电路中,已知 X L XC
U
239.8 55.6V
6.16 8.66
j9 j5
220
30V
-
Z2
U
-
2
U 2
Z2 Z1 Z2
U
2.5 j4 220 8.66 j5
30V
103.6 58V
相量图
U 1
58
55.6
U U
2
注意：U U 1 U 2 U U1 U2
30
I
下列各图中给定的电路电压、阻抗是否正确？
I 解:
Z Z1 Z2 5 53 10 37 Z1 Z2 3 j4 8 j6
+
50 16
U -
Z1
I1Z2 I2
4.47 26.5Ω
11.8 10.5
I1
U Z1
220 0 A 44 5 53
53A
同理：I2
U Z2
220 0 A 22 10 37
37A
I U 220 0 49.2 26.5A Z 4.47 26.5
A
A
I1
I2 C1
B
5Ω j5Ω V
分析：已知电容支路的电流、电压和部分参数
求总电流和电压 解题方法有两种： (1) 用相量(复数)计算
(2) 利用相量图分析求解
j10Ω I
A
I1
A I2 C1
B
5Ω j5Ω V
已知：I1= 10A、 UAB =100V，
求：A、V 的读数
解法1: 用相量计算
设：U AB为参考相量，即：U AB 100 0 V
Z1 Z2
U
Z2
1 Z2
Z1 Z2
+ U
-
I Z
通式: 1 1
Z
Zk
注意：对于阻抗模一般
1 11 Z Z1 Z2
分流公式：I1
Z2 Z1 Z2
I
I2
Z1 Z1 Z2
I
例2:有两个阻抗 Z1 3 j4Ω Z2 8 j6Ω
它们并联接在 U 220 0V的电源上;
求: I1 、I2 和 I 并作相量图。
或 I I1 I2 44 - 53A 22 37A
49.2 26.5A
相量图
26.5
53
I1
37
U
I 注意： I I1 I2
I2
I I1 I2
下列各图中给定的电路电流、阻抗是否正确？
I
I
4A A1 4A A2
4A A1 4A A2
4 4
4 4
(c)
(d)
Z 2Ω I=8A ?
U
U 2
Z2 Z1 Z2
U
3.9阻抗的串联与并联
+
U
例1:
I
有 它两 们个串阻联抗接在Z1U
6.16 220
j9Ω Z 30V
2 2.5
的电源;
求: I 和 U1 、U 2 并作相量图。
j4Ω
Z1
+
-U 1
解：Z
Z1
Z2
(6.16 2.5) j(9
4)
+
8.66 j5 10 30Ω
则该电路呈感性,对不对?
+
U
-
LC
例1：已知: u 220 2 sin ω t V
R 50 Ω , R1 100Ω, X L 200 Ω , XC 400 Ω
求: i i1 , i2
I
分析题目：
+R
已知电源电压和电路参数， 电路结构为串并联。求电流的瞬 时值表达式。
U
-
R1 jX L I1 I2 - jXC
-
Z2
U
-
2
I U 22030 22 0A
Z 1030
U1 Z1I (6.16 j9) 22V 10.9 55.6 22V
239.8 55.6V 同理：U2 Z2I (2.5 j4) 22V 103.6 58V
或利用分压公式：
+ U
I Z1
+
-U 1
+
U 1
Z1 Z1 Z2
U U L U AB 100 j100V
V 读数为141V
100 2 45 V
I U 220 0 A 0.5 33A Z 440 33
I1
Z2 Z1 Z2
I
j400 100 j200
0.5 j400
33A
0.89 - 59.6A
同理：
I2
Z1 Z1 Z2
I
100 j200 0.5 33A 100 j200 j400
I
+ 50Ω 100Ω
U j200Ω I1