拉格朗日方程
- 格式:docx
- 大小:11.88 KB
- 文档页数:2

以约瑟夫·刘易斯·拉格朗日命名的拉格朗日方程是拉格朗日力学的主要方程。
它可以用来描述物体的运动,特别适合于理论物理学的研究。
拉格朗日方程的功能等效于牛顿力学中的牛顿第二定律。
拉格朗日方程:对于一个完整的系统,用广义坐标表示的动力学方程通常指第二种拉格朗日方程,该方程首先由法国数学家J.-L.拉格朗日推导。
通常可以这样写:
其中,t是由广义坐标QJ和广义速度q'j表示的系统动能;QJ 是与QJ对应的广义力;n(= 3n-k)是整个系统的自由度;n是系统的质点数;K是完全约束方程的数量。
完整系统的拉格朗日方程
完整系统的拉格朗日方程
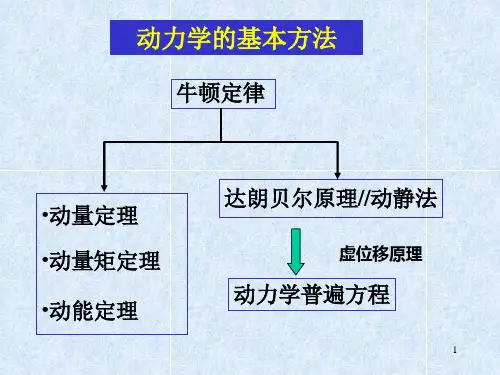
从虚拟位移原理,我们可以得到没有约束力的具有理想约束的粒子系统的平衡方程,而动态静态方法(D'Alembert原理)则采用静态方法来建立粒子系统的动力学方程。
通过将两者结合起来,可以得到没有约束力的粒子系统动力学方程,这是一般的动力学方程。
拉格朗日方程是广义动力学方程在广义坐标系下的具体表达。
拉格朗日方程可用于建立无约束力的动力学方程,也可用于求解在给定运动定律下作用于系统的有功力。
如果要查找约束力,可以将拉格朗日方程与动态和静态方法或动量定理(或质心的运动定理)结合起来。
通常,我们将基于牛顿定律和基于牛顿定律的力学理论称为牛顿力学(也称为矢量力学),将拉格朗日方程和基于其的理论称为拉格朗日力学。
拉格朗日力学描述了机械系统在配置空间中的运动,适合研究受约束粒子系统的运动。
拉格朗日力学在解决微振动和刚体动力学问题中起着重要作用。




拉格朗日方程怎么解
拉格朗日方程,又称为“最优化原理”或“拉格朗日最优化原理”,是一种数
学最优化工具,它可以用来最小化或最大化某一函数。
拉格朗日方程定义如下:
给定n个未知量变量{x1, x2, ..., xn}, 和一个目标函数f(x1, x2, ..., xn) ,
拉格朗日方程的函数由系数与未知变量的函数f(x1, x2, …, xn) 以及拉格
朗日乘子λ的约束条件的乘积组成,即:
L(x1, x2, ..., xn) = f(x1, x2, …, xn) + λ∗g(x1, x2, ..., xn),
其中λ是拉格朗日乘子,g(x1, x2, ..., xn) 是约束条件的乘积。
求解拉格朗日方程的基本思想是:令拉格朗日函数的导数均为零,即L'(x1,
x2, ..., xn)=0.如果给定条件是有界的,那么最优解就是当约束函数值小于0时
达到最小值;而当约束函数值大于0时达到最大值。
拉格朗日方程可以应用于企业管理、最优路线规划、确定最优规模等多领域,
在现实生活中也有着广泛的应用,尤其是在不足以表示信息量和结果的数据中,拉格朗日最优化原理占据重要的地位。
在求解拉格朗日方程时,首先需要确定拉格朗日函数,即把待求解的目标及约束条件全部写入拉格朗日函数,然后令其导数为零,便可求解出拉格朗日方程的最优解。
由此可见,拉格朗日方程是一种有效的最优化方法,它不仅可在数学运算中应用,而且可以在多学科的最优化问题中使用。
拉格朗日方程的使用可以使最优化问题变得简单易行,更方便快捷,对提高企业的管理水平和提升市场竞争力大有裨益。

分析力学拉格朗日方程拉格朗日方程是描述物体在力的作用下运动规律的一个重要工具,是分析力学中的核心内容之一、它由意大利科学家拉格朗日在17世纪末提出,是一种基于能量的方法,对于描述系统的运动非常方便和有效。
拉格朗日方程的形式为:d/dt(dL/dq) - ∂L/∂q = Q,其中L为系统的拉格朗日函数,q表示广义坐标,t表示时间,Q表示外力。
拉格朗日函数L通常由系统的动能和势能函数构成,即L = T - V,其中T表示动能,V表示势能。
拉格朗日方程的推导是基于广义坐标的变分原理,即作用量最小原理。
根据广义坐标的定义,系统的运动可以由广义坐标的函数关系描述。
在运动过程中,系统的作用量S定义为积分∫Ldt,即拉格朗日函数关于时间的积分。
根据变分原理,作用量的真实路径使得作用量的变分δS等于零。
通过变分运算可以得到拉格朗日方程。
拉格朗日方程的形式简洁、便于应用,可以用来描述各种复杂的物体和系统。
它可以用来研究刚体的转动、弹簧振子的运动、多体系统的动力学等。
拉格朗日方程的特点是将系统的动能和势能统一在一个函数中描述,因此能够非常清晰地反映出系统的能量变化情况。
拉格朗日方程的应用可以帮助我们解决物理问题和工程实践中的许多复杂情况。
例如,在机械系统中,可以根据拉格朗日方程求解刚体的绕定轴转动、杆塔的动力学问题等。
在电磁学中,可以使用拉格朗日方程来推导电磁场的变化规律,解决复杂电磁场的问题。
在天体力学中,拉格朗日方程可以用来计算行星、卫星和人造星的轨道运动。
总之,拉格朗日方程是分析力学中的一种重要工具,可以简洁明确地描述物体在力的作用下的运动规律。
它具有普适性和广泛的应用性,对于理解和解决物理问题有着重要的意义。



拉格朗日方程拉格朗日方程(Lagrange Equations)是描述质点系统在广义坐标下的运动的一种方法。
它是由意大利数学家拉格朗日在1755年提出的。
拉格朗日方程是一种非常有用的方法,可以用来解决复杂的力学问题。
本文将阐述拉格朗日方程的概念、定义、推导和应用。
一、拉格朗日方程的概念拉格朗日方程是一种描述物理系统的运动的数学工具。
它是在广义坐标系下描述系统的运动的。
广义坐标系是指可以描述系统运动的坐标系,与传统的笛卡尔坐标系不同。
拉格朗日方程允许我们用少量的代数方程式描述物理系统的运动,而不必考虑物体的确切轨迹。
二、拉格朗日方程的定义拉格朗日方程可以用来描述质点系统的运动。
一个质点系统是由一些质点组成的体系,它们在一起相互作用并受到外力的作用。
拉格朗日方程消除了这些参与到系统运动中的力,并通过一组数学公式描述质点的运动。
这些公式通常由拉格朗日函数和广义坐标定义。
三、拉格朗日方程的推导假设有一个质点系统,它包含了n个质点。
每个质点都有质量m(i),位于位置向量r(i)。
一个质点所受的总力为F(i),则拉格朗日函数为:L = T - V其中,T表示动能,V表示势能,它们都是广义坐标的函数,正好表示质点的位置。
T的公式为:T = 1/2 m(i)*v(i)^2其中,v(i)表示第i个质点的速度向量。
势能V可以描述整个质点系统的势能。
假设在质点系统中有m个约束条件C(k),它们是广义坐标q的函数,如C(k)(q) = 0。
约束条件通常是描述系统中相互作用的限制条件。
根据达朗贝尔原理,可以推导出拉格朗日方程的表达式。
达朗贝尔原理是指系统中所有质点所受力的合力是零,即:∑F(i) = 0假设广义坐标为q = (q1, q2, …, qn),其变化率为dq(i)/dt。
则对于所有的i,可以得到:F(i) = m(i) d^2r(i)/dt^2然后对约束条件C(k)求偏微分:∂C(k) / ∂ri * d^2ri/dt^2 + ∂C(k) / ∂rj * d^2rj/dt^2 = 0其中,i和j分别代表C(k)所属于的质点。

拉格朗日方程式拉格朗日方程式________________________________拉格朗日方程式(Lagrange equation)是物理学中的一个重要概念,主要描述了摩擦力学系统中的动力学特性。
它也是物理学中一个很重要的数学工具,常用于解决简单和复杂力学系统中的力学问题。
它可以用来计算物体在受到外力作用时的动力学行为,从而对物体的运动进行分析和预测。
#### 一、拉格朗日方程式的定义拉格朗日方程式是一种数学方程,它可以用来描述物体在外力作用下的动力学行为。
它的基本形式是:\begin{equation}m\ddot x=F_{ext}-F_{int}\end{equation}其中,$x$是物体的位置向量,$m$是物体的质量,$F_{ext}$是物体受到的外力,$F_{int}$是物体内部受到的内力。
#### 二、拉格朗日方程式的应用拉格朗日方程式在物理学中有广泛的应用,常用于解决各种复杂的力学问题。
例如,在求解物体在受到外力作用时的运动轨迹、求解物体在受到外力作用时的运动规律等问题中,都可以使用拉格朗日方程式来解决。
此外,它还可以用来求解物体在受到外力作用时的运动轨迹、求解物体在受到外力作用时的能量变化、求解物体在受到外力作用时的内部应力等问题。
#### 三、拉格朗日方程式的推导在求解拉格朗日方程式之前,我们需要先了解一些基本概念。
例如,我们需要了解物体受到外力作用时所发生的力学过程,以及物体在这个过程中所受到的力和应力。
具体来说,我们需要了解物体在受到外力作用时所发生的力学过程,以及物体在这个过程中所受到的各种外力和内部应力。
然后,我们就可以使用牛顿定律和能量守恒定律来推导拉格朗日方程式。
依据牛顿定律,我们可以得到:\begin{equation}m\ddot x=F_{ext}-F_{int}\end{equation}而依据能量守恒定律,我们可以得到:\begin{equation}\frac{dK}{dt}+\frac{dU}{dt}=0\end{equation}其中,$K$是物体的动能,$U$是物体的位能。
分析力学拉格朗日方程拉格朗日方程,也称为“拉格朗日原理”,是分析力学中最基本的基本原理,1809年由瑞士物理学家拉格朗日首先提出,被视为一种辩证又统一的基本原理,它给出了复杂系统的一般分析性解,指导着绝大多数物理学问题的研究与解决。
拉格朗日方程提供了一种基本的框架,用于理解物理系统的结构、量子力学,甚至预测物理系统的行为特性,可以说是物理学研究的基础。
拉格朗日方程是一种建立在求解力学问题的基本原理,从基本原理出发,它关注的是力学系统的最优状态。
它强调的是力学系统在力学活动中的最小能量,关注的是力学系统的有效性和稳定性,从而实现力学系统的优化。
拉格朗日方程有两个重要的概念,一个是最小能量原理(也叫拉格朗日能量原理),另一个是最小动力原理(也叫拉格朗日动力原理)。
拉格朗日方程可以用来描述物体在力学影响下的运动,在一定条件下,能够对某些特定物体的运动有判断性的解释,也可以用来求解物体在某特定力学环境下的运动规律。
拉格朗日方程的精髓在于通过研究力学系统的最小能量和最小动力原理,来求解整个力学系统的状态。
这种方法突出了拉格朗日方程求解力学问题的优点:在某一条件下,最小能量原则,可以有效地求解系统中粒子间的最小能量;最小动力原则,可以有效地求解物体在静力学中的最终状态,以及动力学中的力学规律。
拉格朗日方程可以用来推导描述包括机械系统的动力学,量子力学和电动力学等物理系统的最小能量状态和稳定性。
拉格朗日方程的使用对于研究物理系统的最小能量,有效性和稳定性至关重要,它可以帮助科学家们理解和探索物理系统的奥秘,使我们能够实现更精确、更有效地控制物体的运动。
此外,拉格朗日方程也可以用于研究复杂系统中的力学行为,从而推导出复杂系统的力学模型。
对于研究物理系统的运动规律有着关键作用。
总之,拉格朗日方程是一个非常重要的物理系统分析工具,是物理学研究的基础,是分析力学的基本原理。
它的求解可以有效地揭示复杂的力学系统的结构,获得系统的有效性和稳定性,提供物理系统的源泉,对于物理学的研究和理解提供了强有力的指导。
拉格朗日标准方程
拉格朗日标准方程是由法国数学家让·拉格朗日于19世纪中叶首先提出的有关多项式最高次方恒等于零的比较有名的特征方程,它也被称为拉格朗日多项式、拉格朗日多项式方程或L-P方程。
在计算机科学和其他工程领域也被广泛应用。
拉格朗日标准方程一般写为:
a_nx^n + a_{n-1}x^{n-1}+⋯+ a_1x + a_0 = 0
其中,a_n不等于0,n>=1,x是实变量。
拉格朗日标准方程可以通过特征根来求解,特征根就是一组使方程的每个系数都为0的解空间,以及这组解空间的参数值。
特征根的求解方法有很多,例如,可以使用数值积分方法求取,也可以用解析方法解出。
拉格朗日标准方程在计算机科学和其他工程领域应用十分广泛,它可以解决许多工程领域的实际问题。
例如,可以用拉格朗日标准方程来求解最坏情况运行时间,还可以用它来求解最优化问题。
总之,拉格朗日标准方程的实用性已经被证明是极为广泛的。
拉格朗日方程是理论力学中非常重要的方程。
像牛顿力学一样,它是对机械系统的描述。
但是与牛顿力学不同,他从整个系统的角度分析了系统的运动状态,而牛顿力学则分别分析了每个粒子。
这两种方法是等效的,可以相互推论,但使用方案却大不相同。
拉格朗日方程以数学物理学家约瑟夫·拉格朗日(Joseph Lagrange)的名字命名,是分析力学中的重要方程,可用于描述物体的运动,特别适合于理论物理学的研究。
拉格朗日方程的功能等效于牛顿力学中的牛顿第二定律。
假定一个物理系统满足一个完整系统的要求,即所有广义坐标彼此独立,则拉格朗日方程式为:其中,是拉格朗日量,广义坐标,时间函数和广义速度。
以分析力学为指导,有三种方法可以指导拉格朗日方程。
最原始的方法是使用D'Alembert原理来指导Lagrange方程(请参阅D'Alembert原理)。
在更高级的水平上,拉格朗日方程可从哈密顿原理(指哈密顿原理)推导。
最简而言之,它可以通过数学变分方法的欧拉-拉格朗日方程推导:集合函数sum:,,,;哪里是自变量。
如果该函数获得局部平稳值,则Euler-Lagrange方程将保持在区间。
现在,进行以下变换:将自变量设置为时间,将函数设置为广义坐标,并将函数设置为拉格朗日量,从而可以获得拉格朗日方程。
为了满足此转换的正确性,广义坐标必
须彼此独立,因此系统必须是完整的系统。
拉格朗日量是动能减去势,势必须是广义势。
因此,该系统必须是单人系统。