拉格朗日方程

以约瑟夫·刘易斯·拉格朗日命名的拉格朗日方程是拉格朗日力学的主要方程。

它可以用来描述物体的运动，特别适合于理论物理学的研究。

拉格朗日方程的功能等效于牛顿力学中的牛顿第二定律。

拉格朗日方程：对于一个完整的系统，用广义坐标表示的动力学方程通常指第二种拉格朗日方程，该方程首先由法国数学家J.-L.拉格朗日推导。

通常可以这样写：
其中，t是由广义坐标QJ和广义速度q'j表示的系统动能；QJ 是与QJ对应的广义力；n（= 3n-k）是整个系统的自由度；n是系统的质点数；K是完全约束方程的数量。

完整系统的拉格朗日方程
完整系统的拉格朗日方程
从虚拟位移原理，我们可以得到没有约束力的具有理想约束的粒子系统的平衡方程，而动态静态方法（D'Alembert原理）则采用静态方法来建立粒子系统的动力学方程。

通过将两者结合起来，可以得到没有约束力的粒子系统动力学方程，这是一般的动力学方程。

拉格朗日方程是广义动力学方程在广义坐标系下的具体表达。

拉格朗日方程可用于建立无约束力的动力学方程，也可用于求解在给定运动定律下作用于系统的有功力。

如果要查找约束力，可以将拉格朗日方程与动态和静态方法或动量定理（或质心的运动定理）结合起来。

通常，我们将基于牛顿定律和基于牛顿定律的力学理论称为牛顿力学（也称为矢量力学），将拉格朗日方程和基于其的理论称为拉格朗日力学。

拉格朗日力学描述了机械系统在配置空间中的运动，适合研究受约束粒子系统的运动。

拉格朗日力学在解决微振动和刚体动力学问题中起着重要作用。

支持。
其他应用领域
要点一
机器人学
在机器人学中，拉格朗日方程被用于描述机器人的运动规 律。通过建立机器人运动的拉格朗日方程，可以求解出机 器人的关节角度和速度，为机器人的运动控制提供理论依 据。
要点二
生物力学
在生物力学中，拉格朗日方程也被应用于描述生物体的运 动规律。例如，在分析动物的运动行为或人体姿势控制时 ，可以使用拉格朗日方程来描述生物体的运动状态和变化 规律。
解析解法的优缺点分析
优点
解析解法可以得到系统的精确解，适用 于简单模型和特定条件下的复杂模型。
VS
缺点
对于复杂模型，解析解法可能非常困难甚 至无法求解，需要借助数值方法或其他近 似方法。
04
拉格朗日方程的数值解法
数值解法的概念和步骤
概念
数值解法是一种通过数学计算来求解数学问 题的方法，它通过将问题离散化，将连续的 问题转化为离散的问题，然后使用计算机进 行计算求解。
步骤
1.建立数学模型：根据实际问题建立数学模 型，将实际问题转化为数学问题。2.离散化 ：将连续的问题离散化，将连续的时间和空 间划分为若干个小的单元，每个单元称为一 个网格点或节点。3.求解离散化后的方程： 使用数值方法求解离散化后的方程，得到每 个网格点的数值解。4.后处理：对计算结果 进行后处理，提取所需的信息，并进行分析
分析力学基础-拉格 朗日方程
目录
• 引言 • 拉格朗日方程的推导 • 拉格朗日方程的解析解法 • 拉格朗日方程的数值解法 • 拉格朗日方程的应用领域
01
引言
拉格朗日方程的背景和重要性
背景
拉格朗日方程是分析力学中的基 本方程，它描述了系统的运动规 律。
重要性
拉格朗日方程在理论物理、工程 技术和科学研究等领域有着广泛 的应用，是理解和研究复杂系统 运动行为的关键工具。

记
3.1 拉格朗日方程
拉格朗日关系
3.1 拉格朗日方程
由拉格朗日关系
又
3.1 拉格朗日方程
3.1 拉格朗日方程
3.1 拉格朗日方程
（1）动能的显式： 直角坐标 平面极坐标 柱坐标 球坐标
ቤተ መጻሕፍቲ ባይዱ
1 2 T mi r i i 1 2
n
单个质点
x, y , z
r ,
, , z
3.1 拉格朗日方程
[思考2] 滑块作简谐运动
自由度 s 1 ，广义坐标为 ：
X x0 cos t l sin
X l cos
Y l cos Y l sin 约束力 T T sin i T cos j
约束力的虚功
3.2 运动积分 诺特定理
3.2 运动积分 诺特定理
讨论：质点在有心力场中的动能和势能
1 2 2 r 2 T m r 2


k 2m V r
2 1 k m 2 2 2 r L T V m r 2 r


广义坐标：r，
L 0
对应一个循环积分：
3.1 拉格朗日方程
（2）系统势能：（以弹簧原长为弹性势能零点，滑块A所在 平面为重力势能零点）
1 2 V kx m2 gl cos 2
（3）拉格朗日函数：
L T V 1 1 1 2 2 2 2 m 2 l m 2 xl cos kx m 2 gl cos ( m1 m 2 ) x 2 2 2
r Fi i q
n
3.1 拉格朗日方程
3.1 拉格朗日方程

d ∂L ∂L ( )− =0 & dt ∂θ ∂θ
d ∂L 1 2 && & = 3 ml θ d t ∂θ
∂L = −kb 2θ ∂θ
1 2 && ( ml )θ + kb 2θ = 0 3
3kb 2 & θ& + 2 θ = 0 ml
3kb 2 2 ωn = ml 2
n
ωn为圆频率
2 2
ωn 频率：f n = 2π
ri = ri ( q1 , q 2 , L , q k , t ) 则： v i = dri = 因： dt & & & 即： vi = vi (q1 , q2 , L , qk , q1 , q2 , L , qk , t )
广义速度
∂ri ∂r &j + i ∑ ∂q q ∂t j =1 j
k
'
m2 g
δθ
B
δ Wθ Qθ = =0 δθ
δθ ≠ 0
代入拉格朗日方程： 代入拉格朗日方程：
& & (m1 + m2 )&& + m2 Lθ&cosθ − m2 Lθ 2 sinθ + kx = F (t ) x 1 & m2 (2l )2θ& + m2 L&&cosθ + m2 gLsinθ = 0 x 3
动力学的基本方法
牛顿定律
•动量定理 动量定理 •动量矩定理 动量矩定理 •动能定理 动能定理
达朗贝尔原理//动静法 达朗贝尔原理 动静法
虚位移原理
动力学普遍方程

xl
cos

1 2
k
x2

m2
gl
cos
L x

(m1

m2
)
x

m2
l
cos
,
L x

kx
d dt
L x

(m1

m2
)
x
m2
lcos

m2
l
2
sin
L


m2
l
2

m2
xlcos
,
L


m2
xl
sin

m2
glsin
(c)
代入质点系动力学普遍方程，得：
n
n
n
(Fi miai )ri Fi ri miairi 0 (d )
i 1
i 1
i 1
n
Fi
i 1
ri
n
Fi
i 1
( jk1qrij
q
j
kn
) (F
j1 i1
i
ri q j
)q j
kn
质点 M i : mi , 。ri 若取系统的一组广义坐标为
q，1则, q2 ,qk
ri ri (q1,q2 ,qk ,t) (i1,2,n)
(a)
vi
dri dt
jk1qrij
q j
ri t
(i 1,2n)
( b)
称
q j

dq j为广义速度。 dt
7
ri jk1qrij q j (i1,2,n)
22
dL dt

拉格朗日方程是理论力学中非常重要的方程。

像牛顿力学一样，它是对机械系统的描述。

但是与牛顿力学不同，他从整个系统的角度分析了系统的运动状态，而牛顿力学则分别分析了每个粒子。

这两种方法是等效的，可以相互推论，但使用方案却大不相同。

拉格朗日方程以数学物理学家约瑟夫·拉格朗日（Joseph Lagrange）的名字命名，是分析力学中的重要方程，可用于描述物体的运动，特别适合于理论物理学的研究。

拉格朗日方程的功能等效于牛顿力学中的牛顿第二定律。

假定一个物理系统满足一个完整系统的要求，即所有广义坐标彼此独立，则拉格朗日方程式为：其中，是拉格朗日量，广义坐标，时间函数和广义速度。

以分析力学为指导，有三种方法可以指导拉格朗日方程。

最原始的方法是使用D'Alembert原理来指导Lagrange方程（请参阅D'Alembert原理）。

在更高级的水平上，拉格朗日方程可从哈密顿原理（指哈密顿原理）推导。

最简而言之，它可以通过数学变分方法的欧拉-拉格朗日方程推导：集合函数sum：,,,;哪里是自变量。

如果该函数获得局部平稳值，则Euler-Lagrange方程将保持在区间。

现在，进行以下变换：将自变量设置为时间，将函数设置为广义坐标，并将函数设置为拉格朗日量，从而可以获得拉格朗日方程。

为了满足此转换的正确性，广义坐标必
须彼此独立，因此系统必须是完整的系统。

拉格朗日量是动能减去势，势必须是广义势。

因此，该系统必须是单人系统。

分析力学拉格朗日方程拉格朗日方程是描述物体在力的作用下运动规律的一个重要工具，是分析力学中的核心内容之一、它由意大利科学家拉格朗日在17世纪末提出，是一种基于能量的方法，对于描述系统的运动非常方便和有效。

拉格朗日方程的形式为：d/dt(dL/dq) - ∂L/∂q = Q，其中L为系统的拉格朗日函数，q表示广义坐标，t表示时间，Q表示外力。

拉格朗日函数L通常由系统的动能和势能函数构成，即L = T - V，其中T表示动能，V表示势能。

拉格朗日方程的推导是基于广义坐标的变分原理，即作用量最小原理。

根据广义坐标的定义，系统的运动可以由广义坐标的函数关系描述。

在运动过程中，系统的作用量S定义为积分∫Ldt，即拉格朗日函数关于时间的积分。

根据变分原理，作用量的真实路径使得作用量的变分δS等于零。

通过变分运算可以得到拉格朗日方程。

拉格朗日方程的形式简洁、便于应用，可以用来描述各种复杂的物体和系统。

它可以用来研究刚体的转动、弹簧振子的运动、多体系统的动力学等。

拉格朗日方程的特点是将系统的动能和势能统一在一个函数中描述，因此能够非常清晰地反映出系统的能量变化情况。

拉格朗日方程的应用可以帮助我们解决物理问题和工程实践中的许多复杂情况。

例如，在机械系统中，可以根据拉格朗日方程求解刚体的绕定轴转动、杆塔的动力学问题等。

在电磁学中，可以使用拉格朗日方程来推导电磁场的变化规律，解决复杂电磁场的问题。

在天体力学中，拉格朗日方程可以用来计算行星、卫星和人造星的轨道运动。

总之，拉格朗日方程是分析力学中的一种重要工具，可以简洁明确地描述物体在力的作用下的运动规律。

它具有普适性和广泛的应用性，对于理解和解决物理问题有着重要的意义。

理想弹性振子的振动分析
总结词
理想弹性振子是一个简化的模型，用于研究振动的规 律。通过拉格朗日方程，可以分析其振动行为。
详细描述
理想弹性振子是一个质量为m的质点，连接到一个无 质量的弹簧上。当振子受到一个外部力作用时，它会 开始振动。通过应用拉格朗日方程，可以计算出振子 的振动频率和振幅。
地球的运动分析
详细描述
分离变量法是一种求解偏微分方程的常用方法。它通过假设解可以表示为多个独立变量的乘积，将偏微分方程转 化为多个常微分方程，从而简化了求解过程。这种方法在求解波动方程、热传导方程等偏微分方程时非常有效。
哈密顿正则方程法
总结词
利用哈密顿原理和正则方程推导出系统 的运动方程，适用于完整约束系统。
VS
相对论力学中的拉格朗日方程
总结词
相对论力学中的拉格朗日方程是经典拉格朗 日方程的进一步发展，它考虑了相对论效应 ，适用于高速运动和高能量密度的物理系统 。
详细描述
在相对论力学中，由于物体的高速运动和相 对论效应的影响，经典拉格朗日方程需要进 行相应的修正。相对论力学中的拉格朗日方 程能够更好地描述高速运动和高能量密度下 的物理过程，如相对论性粒子的运动、高能
要点一
总结词
地球的运动是一个复杂的系统，涉及到多个力和力的矩。 通过拉格朗日方程，可以分析地球的运动轨迹和规律。
要点二
详细描述
地球的运动包括自转和公转，受到太阳和其他天体的引力 作用。通过应用拉格朗日方程，可以计算出地球的运动轨 迹和周期，以及地球上不同地区的重力加速度和潮汐现象 等。
非保守系统的拉格朗日方程
总结词
非保守系统中的拉格朗日方程需要考虑非保 守力的影响，这需要引入额外的变量和方程 来描述系统的运动。

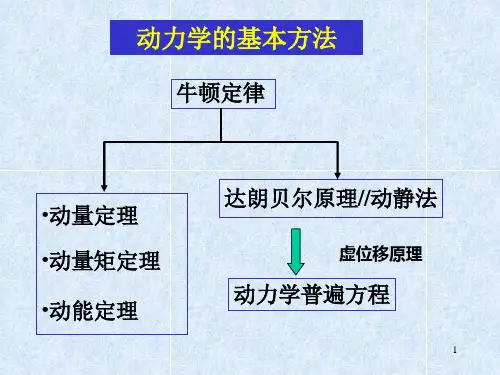
第3章拉格朗日方程以动力学普遍方程为基础，拉格朗日导出了两种形式的动力学方程，分别称为第一类和第二类拉格朗日方程。

将达朗贝尔原理与虚位移原理相结合，建立起动力学普遍方程，避免了理想约束力的出现；再把普遍方程变为广义坐标形式，进一步转变为能量形式，导出了第二类拉格朗日方程，实现了用最少数目的方程描述动力系统；应用数学分析中的乘子法，采用直角坐标形式的普遍方程和约束方程而建立的一组动力学方程，是第一类拉格朗日方程，便于程式化处理约束动力系统问题。

拉格朗日方程是分析力学得以发展之源。

3.1 第二类拉格朗日方程第二类拉格朗日方程是分析力学中最重要的动力学方程，它给出动力学问题一个普遍、简单而又统一的解法。

拉格朗日方程只适用于完整约束的质点系。

3.1.1 几个关系式的推证为方便起见，在推导拉格朗日方程前，先推证几个关系式。

质点系由n个质点、s个完整的理想约束组成，它的自由度数为k＝3n–s，广义坐标数与自由度数相等。

该系统中，任一质点M i的矢径r i可表示成广义坐标q1，q2，…，q k和时间t的函数，即r i＝r i(q1，q2，…，q k，t)i＝1,2,…,n它的速度(3-1)i＝1,2,…,n式中称为h个广义坐标的广义速度，分别为广义坐标和时间的函数，与广义速度没有直接的关系。

式(3-1)对求偏导数，则有(3-2)这是推证的第一个关系式，它表明，任一质点的速度对广义速度的偏导数等于其矢径对广义坐标的偏导数。

为推证第二个关系式，将式(3-1)对广义坐标q j求偏导数，或(3-3)这是第二个关系式，它表明，任一质点的速度对广义坐标的偏导数等于其矢径对广义坐标的偏导数，再对时间的一阶导数。

再看看质点的动能对广义坐标的偏导数。

有(A)又式(3-2)、式(3-3)代入上式，并注意式(A)的关系，(3-4)3.1.2 第二类拉格朗日方程动力学普遍方程可以改写为(3-5)左侧的第一项主动力的虚功之和，可以用广义力Q h在广义虚位移q h上所做的功之和表示，即(3-6)值得指出，这里的主动力并非平衡问题中的主动力，因此，这里的广义力Q h不等于零。

拉格朗日方程拉格朗日方程(Lagrange Equations)是描述质点系统在广义坐标下的运动的一种方法。

它是由意大利数学家拉格朗日在1755年提出的。

拉格朗日方程是一种非常有用的方法，可以用来解决复杂的力学问题。

本文将阐述拉格朗日方程的概念、定义、推导和应用。

一、拉格朗日方程的概念拉格朗日方程是一种描述物理系统的运动的数学工具。

它是在广义坐标系下描述系统的运动的。

广义坐标系是指可以描述系统运动的坐标系，与传统的笛卡尔坐标系不同。

拉格朗日方程允许我们用少量的代数方程式描述物理系统的运动，而不必考虑物体的确切轨迹。

二、拉格朗日方程的定义拉格朗日方程可以用来描述质点系统的运动。

一个质点系统是由一些质点组成的体系，它们在一起相互作用并受到外力的作用。

拉格朗日方程消除了这些参与到系统运动中的力，并通过一组数学公式描述质点的运动。

这些公式通常由拉格朗日函数和广义坐标定义。

三、拉格朗日方程的推导假设有一个质点系统，它包含了n个质点。

每个质点都有质量m(i)，位于位置向量r(i)。

一个质点所受的总力为F(i)，则拉格朗日函数为：L = T - V其中，T表示动能，V表示势能，它们都是广义坐标的函数，正好表示质点的位置。

T的公式为：T = 1/2 m(i)*v(i)^2其中，v(i)表示第i个质点的速度向量。

势能V可以描述整个质点系统的势能。

假设在质点系统中有m个约束条件C(k)，它们是广义坐标q的函数，如C(k)(q) = 0。

约束条件通常是描述系统中相互作用的限制条件。

根据达朗贝尔原理，可以推导出拉格朗日方程的表达式。

达朗贝尔原理是指系统中所有质点所受力的合力是零，即：∑F(i) = 0假设广义坐标为q = (q1, q2, …, qn)，其变化率为dq(i)/dt。

则对于所有的i，可以得到：F(i) = m(i) d^2r(i)/dt^2然后对约束条件C(k)求偏微分：∂C(k) / ∂ri * d^2ri/dt^2 + ∂C(k) / ∂rj * d^2rj/dt^2 = 0其中，i和j分别代表C(k)所属于的质点。

17.2
板上有半径为 r 、 质量为m2的均质圆柱， 圆柱在板
上作纯滚动而不滑动，今有一水平常力F 拉动金属
板，试求圆柱纯滚的角加速度和金属板的加速度。
拉
解：以系统为研究对象，
格
系统具两个自由度。选取 x A、
为广 义坐标。
C m2 g
A
朗 日 方
系统的动能为
xA
m1g
T

1 2
m1xA2

1 2
(1 12
m2 L2
)2
整理后得
T

3 4
m1x2

1 2
m2 (x2

1 4
L22

Lxcos)
1 24
m2 L22
系统的广义力为 Qx 0
17.2
Q

W ( )

m2 g
L 2

cos (90
)

xm2 g
L sin
一、拉格朗日方程
设有n个知点组成的知点系，受完整的理想约束，
17.2 具有k个自由度，其位置可由k个广义坐标 q1, q2 ,, qk
来确定。则有
拉 格
d ( T ) T dt qj q j
Qj
( j 1,2,, k)
朗
日
式中
T

n i 1
12mi vi2 为质点系的动能；
M
r
O
拉 为R。今在曲柄上作用一不变的力
R
格
偶，其矩为M，使机构运动。求曲 柄的运动方程。
朗
解：以整个系统为研究对象，系统具有一个自
日 由度，取曲柄转角 为广义坐标。

d dt
(
L qr
)
L qr
0
24
积分得：
L qr
C
(常数)
(rk)
循环积分
因L = T - U，而U中不显含 qr ，故上式可写成
L qr
qr
(T
U
)
T qr
Pr
C
(常数)
Pr称为广义动量，因此循环积分也可称为系统的广义动量积分。 保守系统对应于循环坐标的广义动量守恒。
能量积分和循环积分都是由保守系统拉格朗日方程积分一 次得到的，它们都是比拉格朗日方程低一阶的微分方程。
12 g
W ( ) M
Q
W (
)
M
T
1 6
2P
9Q g
(R r)2
;
d dt
T
1 6
2P
9Q g
(
R
r)
2
;
T
0
15
代入拉氏方程：
1 2P 9Q (R r)2 0 M
6g
6M
g
(2P 9Q)(R r)2
积分，得：
3M (2 P 9Q )(R r ) 2
gt
2
C1t
C2
代入初始条件，t =0 时， 0 0 , 0 0 得 C1 C2 0
故：
3M
gt 2
(2P9Q)( Rr)2
16
[例2] 与刚度为k 的弹簧相连的滑块A，质量为m1,可在光 滑水平面上滑动。滑块A上又连一单摆，摆长l ， 摆锤质量为 m2 ，试列出该系统的运动微分方程。
解：将弹簧力计入主 动力，则系统成为具 有完整、理想约束的 二自由度系统。保守
系统。取x , 为广义

拉格朗日方程（Lagrange's equations）和虚功原理（Principle of Virtual Work）都是理论力学中常用的分析方法，用于描述物体的运动和力学系统的行为。

拉格朗日方程是描述质点或物体在广义坐标下的运动的方程。

它是源自哈密顿原理（Hamilton's principle），通过定义一个称为拉格朗日量（Lagrangian）的函数来推导得到。

拉格朗日量是系统动能与势能的差，其定义为L = T - V，其中T 是动能，V 是势能。

拉格朗日方程可以统一描述多自由度系统中质点或刚体的运动，通过求解其中的偏微分方程可以得到物体的运动方程。

虚功原理是一个广义的力学原理，用于分析力学系统中的约束。

它通过平衡约束力和虚位移所作的虚功为零来得到系统的运动方程。

虚功原理要求系统在一组虚位移下保持等势，即满足约束条件。

通过应用虚功原理，可以推导出与拉格朗日方程等价的运动方程。

虚功原理和拉格朗日方程都是建立在能量守恒原理的基础上，它们提供了一种简洁而深入的方法来描述物体的运动和约束行为。

它们在理论力学、动力学、弹性力学等领域具有重要的应用价值。

拉格朗日方程（Lagrange's equations）给出了描述力学系统中物体运动的一阶微分方程。

在一般的情况下，拉格朗日方程可以表示为：d/dt (∂L/∂ᶲ̇ᵢ) - ∂L/∂ᶲᵢ = Qᵢ其中，L 是系统的拉格朗日量，ᶲ是广义坐标（generalized coordinates），ᶲ̇是对应的广义速度（generalized velocities），Qᵢ是外力对应的广义力（generalized forces）。

在使用拉格朗日方程求解力学系统时，我们首先选择适当的广义坐标，构建系统的拉格朗日量。

然后，对拉格朗日量分别对广义速度和广义坐标求偏导，并对时间求导，得到上述方程中的项。

最后，根据外力对应的广义力，求解该方程可以得到系统的运动方程。

拉格朗日方程式拉格朗日方程式________________________________拉格朗日方程式（Lagrange equation）是物理学中的一个重要概念，主要描述了摩擦力学系统中的动力学特性。

它也是物理学中一个很重要的数学工具，常用于解决简单和复杂力学系统中的力学问题。

它可以用来计算物体在受到外力作用时的动力学行为，从而对物体的运动进行分析和预测。

#### 一、拉格朗日方程式的定义拉格朗日方程式是一种数学方程，它可以用来描述物体在外力作用下的动力学行为。

它的基本形式是：\begin{equation}m\ddot x=F_{ext}-F_{int}\end{equation}其中，$x$是物体的位置向量，$m$是物体的质量，$F_{ext}$是物体受到的外力，$F_{int}$是物体内部受到的内力。

#### 二、拉格朗日方程式的应用拉格朗日方程式在物理学中有广泛的应用，常用于解决各种复杂的力学问题。

例如，在求解物体在受到外力作用时的运动轨迹、求解物体在受到外力作用时的运动规律等问题中，都可以使用拉格朗日方程式来解决。

此外，它还可以用来求解物体在受到外力作用时的运动轨迹、求解物体在受到外力作用时的能量变化、求解物体在受到外力作用时的内部应力等问题。

#### 三、拉格朗日方程式的推导在求解拉格朗日方程式之前，我们需要先了解一些基本概念。

例如，我们需要了解物体受到外力作用时所发生的力学过程，以及物体在这个过程中所受到的力和应力。

具体来说，我们需要了解物体在受到外力作用时所发生的力学过程，以及物体在这个过程中所受到的各种外力和内部应力。

然后，我们就可以使用牛顿定律和能量守恒定律来推导拉格朗日方程式。

依据牛顿定律，我们可以得到：\begin{equation}m\ddot x=F_{ext}-F_{int}\end{equation}而依据能量守恒定律，我们可以得到：\begin{equation}\frac{dK}{dt}+\frac{dU}{dt}=0\end{equation}其中，$K$是物体的动能，$U$是物体的位能。

定义：拉格朗日方程，因约瑟夫·路易斯·拉格朗日而命名，是拉格朗日力学的主要方程，可以用来描述物体的运动，特别适用于理论物理的研究。

拉格朗日方程的功能相等于牛顿力学中的牛顿第二定律。

拉格朗日方程：对于完整系统用广义坐标表示的动力方程，通常系指第二类拉格朗日方程,是法国数学家J.-L.拉格朗日首先导出的。

通常可写成：式中T为系统用各广义坐标qj和各广义速度q'j所表示的动能；Qj为对应于qj 的广义力;N(=3n-k)为这完整系统的自由度；n为系统的质点数；k为完整约束方程个数。

从虚位移原理可以得到受理想约束的质点系不含约束力的平衡方程，而动静法(达朗贝尔原理)则将列写平衡方程的静力学方法应用于建立质点系的动力学方程，将这两者结合起来，便可得到不含约束力的质点系动力学方程,这就是动力学普遍方程。

而拉格朗日方程则是动力学普遍方程在广义坐标下的具体表现形式。

拉格朗日方程可以用来建立不含约束力的动力学方程，也可以用来在给定系统运动规律的情况下求解作用在系统上的主动力。

如果要想求约束力，可以将拉格朗日方程与动静法或动量定理(或质心运动定理)联用。

通常，我们将牛顿定律及建立在此基础上的力学理论称为牛顿力学(也称矢量力学)，将拉格朗日方程及建立在此基础上的理论称为拉格朗日力学。

拉格朗日力学通过位形空间描述力学系统的运动，它适合于研究受约束质点系的运动。

拉格朗日力学在解决微幅振动问题和刚体动力学的一些问题的过程中起了重要的作用。

拉格朗日插值公式（外文名Lagrange interpolation formula）指的是在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值的一种插值多项式。

公式线性插值也叫两点插值，已知函数y = f(x)在给定互异点x0, x1上的值为y0= f(x0)，y1= f(x1)线性插值就是构造一个一次多项式P1(x) = ax + b使它满足条件P1(x0) = y0P1(x1) = y1其几何解释就是一条直线，通过已知点A (x0, y0)，B(x1, y1)。

拉格朗日方程公式拉格朗日方程公式是经典力学中一种重要的数学工具，它描述了物体在给定势能场下的运动规律。

拉格朗日方程公式的提出，极大地简化了力学问题的求解，使得我们能够更轻松地研究物体的运动轨迹和力学性质。

拉格朗日方程公式由法国数学家约瑟夫·路易斯·拉格朗日于18世纪提出，它是一种基于能量守恒原理的描述力学系统的数学表达式。

拉格朗日方程公式的基本思想是，一个力学系统的运动可以通过一个称为拉格朗日量的函数来描述，该函数是广义坐标和广义速度的函数。

通过对拉格朗日量求导数，再根据欧拉-拉格朗日方程，我们可以得到描述系统运动的微分方程。

拉格朗日方程公式的形式为：d/dt(∂L/∂q i) - ∂L/∂qi = 0其中，L是拉格朗日量，qi是广义坐标，q i是广义速度，t是时间。

这个方程描述了力学系统的运动方程，它将系统的运动规律与系统的势能、动能以及约束条件联系起来。

拉格朗日方程公式的优点在于它可以将力学问题转化为求解一组常微分方程的问题，避免了传统的牛顿力学中需要解决大量的二阶常微分方程的困难。

通过拉格朗日方程公式，我们可以更加直观地理解力学系统的运动规律，并且可以应用于各种复杂的力学问题的求解。

除了在经典力学中的应用，拉格朗日方程公式在其他物理学领域也有广泛的应用。

例如，在电动力学中，我们可以通过拉格朗日方程公式来推导出麦克斯韦方程组，描述电磁场的传播和相互作用规律。

在量子力学中，拉格朗日方程公式也被广泛应用于描述微观粒子的运动和相互作用。

拉格朗日方程公式是一种重要的数学工具，它在经典力学和其他物理学领域中具有广泛的应用价值。

它的提出极大地简化了力学问题的求解，使得我们能够更加深入地研究物体的运动规律和力学性质。

通过掌握和应用拉格朗日方程公式，我们可以更好地理解和解决各种力学问题，推动科学的发展和进步。

拉格朗日标准方程
拉格朗日标准方程是由法国数学家让·拉格朗日于19世纪中叶首先提出的有关多项式最高次方恒等于零的比较有名的特征方程，它也被称为拉格朗日多项式、拉格朗日多项式方程或L-P方程。

在计算机科学和其他工程领域也被广泛应用。

拉格朗日标准方程一般写为：
a_nx^n + a_{n-1}x^{n-1}+⋯+ a_1x + a_0 = 0
其中，a_n不等于0，n>=1，x是实变量。

拉格朗日标准方程可以通过特征根来求解，特征根就是一组使方程的每个系数都为0的解空间，以及这组解空间的参数值。

特征根的求解方法有很多，例如，可以使用数值积分方法求取，也可以用解析方法解出。

拉格朗日标准方程在计算机科学和其他工程领域应用十分广泛，它可以解决许多工程领域的实际问题。

例如，可以用拉格朗日标准方程来求解最坏情况运行时间，还可以用它来求解最优化问题。

总之，拉格朗日标准方程的实用性已经被证明是极为广泛的。