当前位置：文档之家 › 拉格朗日方程漫谈(第二讲)

拉格朗日方程漫谈(第二讲)

  • 格式：pdf
  • 大小：351.24 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

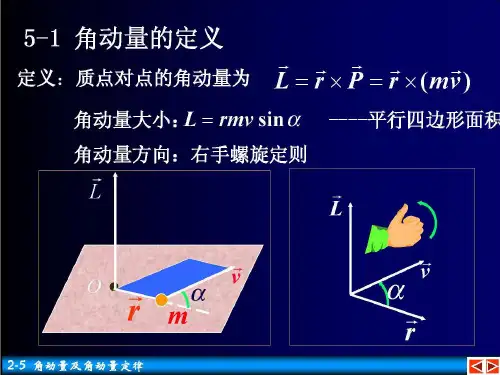
2_拉格朗日方程

2_拉格朗日方程

O

(x1,y1)

A
P1
(x2,y2) B(x3,y3)
P2
F
(1)
由已知条件可得
x1
1 2
l1 sin 1 l 2 sin (2)
x 2 l1 sin
2 y 3 l1 cos l 2 cos
把(2) 式代入(1) 式得
P1 (
1 2
l1 sin ) P2 ( l1 sin
x i x i ( q1 , q 2 , , q s , t ) y i y i ( q1 , q 2 , , q s , t ) z i z i ( q1 , q 2 , , q s , t )
或 式中
( i 1, 2 , , n , s 3 n )
ri ri ( q 1 , q 2 , , q s , t )
以上分量式若改用s 个独立广义坐标表示，然后令s 个独立的 虚位移前的乘数等于零，则可得出所求的平衡条件。 若求约束力，则要利用拉格朗日未定乘数。 广义坐标下 ri 的虚位移为
ri

n
s
ri
由此得广义坐标下的平衡方程是
W

Q
1
q
q 0
s
F
i 1 s
n
i n
i 1
虚功原理：受理想约束的力学体系平衡的充要条件是此力学 体系的诸主动力在任意虚位移中所做的元功之和为零。这就 是虚功原理，也叫虚位移原理。是1717年伯努利首先发现。 对于理想约束体系，利用虚功原理可以方便的求出主动力满 足的平衡条件，但无法求出约束反力。 由于约束，3n 个坐标不独立，即作用在任一质点上的合外 力在虚位移方向上的投影，一般不会全令之为零。否则就可 能变成n 个自由质点的平衡方程。

拉格朗日第二类方程

拉格朗日第二类方程

拉格朗日第二类方程
拉格朗日第二类方程是经典力学中的基础概念之一。

它描述的是质点
在一定约束下的运动，是建立在尺度不变性原理的基础上的。

下面我
将按照以下列表分别介绍拉格朗日第二类方程的定义、推导过程以及
其应用。

1. 定义：
拉格朗日第二类方程是描述系统动力学的数学模型，它是由勒让德在1797年建立的，具体形式为：
d/dt (∂L/∂qᵢ) − ∂L/∂qᵢ = Qᵢ
其中，L是系统的拉格朗日函数，q是系统的广义坐标，Q是系统的非
保守力。

2. 推导过程：
拉格朗日第二类方程的推导主要分为以下几个步骤：
第一步，构建系统的拉格朗日函数，即L=T-V，其中T是系统的动能，V是系统的势能。

第二步，求出系统的广义动量pᵢ=∂L/∂qᵢ。

第三步，对广义动量求导得到系统的加速度aᵢ= d/dt (∂L/∂qᵢ)。

第四步，根据牛顿第二定律F=ma以及广义动量的定义pᵢ=∂L/∂qᵢ，将非保守力Q用广义动量表示为Qᵢ=∂V/∂qᵢ。

第五步，代入广义动量和非保守力的表达式，得到拉格朗日第二类方程d/dt (∂L/∂qᵢ) − ∂L/∂qᵢ = Qᵢ。

3. 应用：
拉格朗日第二类方程是经典力学中最基础的方程之一，它在物理学的各个领域都有广泛的应用，如
（1）陀螺的运动学研究
（2）杆的运动学研究
（3）学习简谐振动的方程
（4）学习经典电动力学中的运动方程
（5）学习光学中的光路方程等
总之，拉格朗日第二类方程在物理学研究中有着重要的地位，熟练掌握它的概念和应用对于探究自然界的规律和解决实际问题都具有重要作用。

拉格朗日方程2

拉格朗日方程2
n
∂r & m&i ⋅ i ∑ ir ∂q i= 1 k
n n ∂r d d ∂r & ⋅ i ) −∑ ir ⋅ ( i ) & = ∑ i (r m mi i dt ∂qk dt ∂qk i= 1 i= 1 n
∂r N ∂r & & r = i +∑ i qk i ∂t k=1 ∂qk
& qk =
x
解：2、施加惯性力
y A δx OC a1
FI 2 r
MI2
δϕ D C2 α
m2 g FI 2 e
F = ma I1 1 1
F =m a I2e 2 1
ae C1
FI1
F = m ar I2r 2
MI2 = J2 α2 1 J2 = m R2 2 2
ar B
x
m1g
解：3、确定虚位移 考察三棱柱和圆盘组成的 系统，系统具有两个自由度。 系统，系统具有两个自由度。 二自由度系统具有两组虚 位移： 位移： 第一组
q = (q1 ,q2 ,⋅⋅⋅,qN )
ri =ri (q , q2,⋅⋅⋅, qN ,t) 1
∑F ⋅δ r −∑ma ⋅δ r =0
i= 1 i i i= 1 i i i N k k
n
n
∑F ⋅δ r = ∑Q δq
1 i= i i 1 k=
n
Qk——广义力
N n ∂r ∂r i & & mr ( mr mai ⋅δ ri = ∑ i&i ⋅ ∑ δqk = ∑ ∑ i&i ⋅ i )δqk ∑i ∂qk i= 1 k= ∂ k 1 q k= i= 1 1 i= 1
y A δx OC

简称拉格朗日方程

简称拉格朗日方程
本章研究拉格朗日第二类方程（简称拉格朗日方程）。他是研究动力学问 题的又一有力手段，在解决非自由质点系的动力学问题时，显得十分简捷、规 范。
§17-1 广义力 以广义力表示的质点系的平衡条件
一、广义力 设有n个质点组成的质点系，具有k个自由度，可由k个广义坐标q1， q2，... ，
qk 确定其位置。在非定常约束下，质点系中任一质点Mi的矢径
一、拉格郎日方程
设有n个质点组成的质点系，具有k个自由度，可由k个广义坐标q1， q2，... ， qk 确定其位置。在非定常约束下，质点系中任一质点Mi的矢径
Mi的虚位移（固定时间t）：
代入质点系动力学普遍方程：
第一项：主动力在质点系的虚位移的元功之和：
n
k
Fi ri Qj q j
i 1
i
yi q j
j zi k ) q j
2、实际应用时，由
k
W Qjq j Q1q1 Q2q2 ... Qkqk j 1
由于各广义坐标彼此独立，所以在求某个广义力Qj时，仅使对应的广义坐 标qj变分 qj，而其余的广义坐标则保持不变。即：令 qj≠0， qi=0（i=1，2， ...n，i ≠ j），
d dt
(mi
vi
ri q j
)
mi
vi
d ri dt q j
为简化上式 , 需要用到以下两个关系式：
(f)
①Mi点的速度： 由(a)式
vi
dri dt
ri q1
q1
ri q2
q2 ...
ri qk
qk
ri t
k
ri
j1 q j
qj
ri t
(g)
式中：qj — 广义速度

理论力学(Ⅱ)—拉格朗日方程59页PPT

理论力学(Ⅱ)—拉格朗日方程59页PPT

46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特
理论力学(Ⅱ)—拉格朗日方程
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克

第2章 拉格朗日方程

第2章 拉格朗日方程
在数论方面，拉格朗日也显示出非凡的才能。他对费马提出的许多问题作出了解答。如，一个正整数是不多于4个平方数的和的问 题等等，他还证明了圆周率的无理性。这些研究成果丰富了数论的内容。 在《解析函数论》以及他早在1772年的一篇论文中，在为微积分奠定理论基础方面作了独特的尝试，他企图把微分运算归结为代数运 算，从而抛弃自牛顿以来一直令人困惑的无穷小量，并想由此出发建立全部分析学。但是由于他没有考虑到无穷级数的收敛性问题， 他自以为摆脱了极限概念，其实只是回避了极限概念，并没有能达到他想使微积分代数化、严密化的目的。不过，他用幂级数表示函 数的处理方法对分析学的发展产生了影响，成为实变函数论的起点。
2. 具有简单统一的微分方程；
力学体系不同
分析力学：力学量 L(T,V) 或 H(T,V) 不同. 牛顿力学：运动微分方程不同.
3. 使用范围更广
能量概念适用于量子力学，甚至非力学体系；
..
量子力学中的 r, , r, 等是没有意义的.
4. 扩大了坐标的概念、引入广义坐标
n 个质点，k 个约束
牛顿力学：3n k 个方程；
分析力学
分析力学主要内容:
约束与广义坐标 虚功原理 拉格朗日方程 小振动 哈密顿正则方程 泊松括号与泊松定理 哈密顿原理 正则变换 哈密顿—雅科比理论
导论
一. 研究机械运动的着眼点
牛 顿 力 学 （ 矢 量 力 学）力动量F 2pm2V(Tr)动势能能分 析 力 学
二. 分析力学的特点
1. 把力学系统作为一个整体考虑 (牛顿力学是先质 点、再质点系 );
如果约束方程不仅包含质点的坐标, 还包含坐标对 时间的导数或坐标的微分, 而且不能通过积分使之 转化为仅包含坐标和时间的完整约束方程, 则这种 约束称为非完整约束, 其约束方程形式为

06-分析力学基础-第二类拉格朗日方程资料

06-分析力学基础-第二类拉格朗日方程资料

保守体系的拉格朗日方程为：
d dt
(qLk)qLk
0
想一想：上式的成立、适用条件是什么？
M1-6
3. 对拉格朗日方程的评价
(1) 拉氏方程的特点（优点）： 是一个二阶微分方程组，方程个数与体系的自由度相同。形式简 洁、结构紧凑。而且无论选取什么参数作广义坐标，方程形式不变。 方程中不出现约束反力，因而在建立体系的方程时，只需分析已 知的主动力，不必考虑未知的约束反力。体系越复杂，约束条件越 多，自由度越少，方程个数也越少，问题也就越简单。
M1-10
系统动能：
T1 2m 1x21 2JBB 21 2JI
2 A
1 2 m 1 x 2 1 2 1 2 m 2 R 2B 2 1 2 2 3 m 2 R 2A 2
m1
2m2 2
x2
系统的拉格朗日函数（动势）
LTV m 1 2 2 m 2x 2 1 2 k (0 x )2 m 1 g x
5. 求出上述一组微分方程的积分。
M1-9
[例] 物块C的质量为m1，A，B两轮 皆为均质圆轮，半径R，质量为m2， 求系统的运动微分方程。
解：图示机构只有一个自由度，所受
约束皆为完整、理想、定常的，以物 块平衡位置为原点，取x 为广义坐标。
系统势能： (以弹簧原长为弹性势能零点)
V1 2k(0x)2m1gx
2. 计算质点系的动能T，表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j(j 1 ,2 , ,k)，计算公式为：
Q j i n1(Xi q xijYi q yijZi q zij) 或
Qj
W ( j) qj
若主动力为有势力，也可将势能 V 表示为广义坐标的函数。

分析力学基础-第二类拉格朗日方程

分析力学基础-第二类拉格朗日方程

i n1mid dtr& iq & r& iki n1mir& iqr& ik
d d ti n1 m ir & i q & r & ik qki n11 2m ir & ir & i
d d t q & ki n11 2m ivi2 qki n11 2m ivi2
d dt
qT&k
Qj
W ( j) qj
若主动力为有势力，也可将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理，得出k个二阶常微分方程。
5. 求出上述一组微分方程的积分。
.
M1-9
[例] 物块C的质量为m1，A，B两轮 皆为均质圆轮，半径R，质量为m2， 求系统的运动微分方程。
解：图示机构只有一个自由度，所受
约束皆为完整、理想、定常的，以物 块平衡位置为原点，取x 为广义坐标。
系统势能： (以弹簧原长为弹性势能零点)
V1 2k(0x)2m1gx
.
M1-10
系统动能：
T1 2m 1x & 21 2JBB 21 2JI
2 A
1 2 m 1 x & 2 1 2 1 2 m 2 R 2B 2 1 2 2 3 m 2 R 2A 2
应用拉氏方程解题的步骤：
1. 判定质点系的自由度k，选取适宜的广义坐标。必须注意： 不能遗漏独立的坐标，也不能有多余的（不独立）坐标。
2. 计算质点系的动能T，表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j(j1,2,L,k)，计算公式为：
Q j i n1(Xi q xijYi q yijZi q zij) 或

第二类拉格朗日方程

第二类拉格朗日方程

[1/1页][返回]达朗伯原理能将动力学问题转化为静力学问题，虚位移原理是分析静力学的普遍原理；因而，两者结合就能导出分析动力学的普遍方程。

对完整系统，拉格朗日方程是实用的建立动力学方程的方法。

§18-1 动力学普遍方程质系由n 个质点组成。

根据达朗伯原理，在每个质点的主动力F i 、约束力及惯性力平衡。

再根据虚位移原理，它们在质系虚位移上元功之和应为零。

即对受理想约束系统有(18-1)上式称为达朗伯-拉格朗日原理或动力学普遍方程，其直角坐标表达式为(18-2)例18-1 动滑轮上悬挂重物质量为，另一重物质量为，忽略轮、绳的质量及轮轴摩擦，求下降的加速度。

解：（1）考虑整个系统为研究对象，系统具有理想约束，主动力为重力g及g。

引入假想的惯性力F g1及 F g2，方向如图，其大小为则系统平衡。

（2）给系统以虚位移及，则由动力学普遍方程(18-2) 有系统具有一个自由度，由约束关系代入上式，故有例18-2 二均质轮的，求在重力作用下轮Ⅱ中心的加速度。

解：（1）解法一：考虑整个系统，引入惯性力F g及惯性力偶，大小为, ,其中，，为轮Ⅱ中心的加速度及二轮的角加速度。

由动力学普遍方程由约束关系有,①代入上式系统有二自由度，与相互独立，故有,解之得（2）解法二：加惯性力后，按下法给虚位移。

令，，计算虚功(考虑约束关系)∴令，，计算虚功∴与前面一样可解出§18-2 拉格朗日方程1. 动力学普遍方程在广义坐标中的表达式设系统的广义坐标为,则有（18-3）（18-4）代入动力学普遍方程（18-1）引入 ,（18-5）其中按第十七章称为广义力；仿此，称为广义惯性力。

∴受完整约束的系统中，相互独立，上式中前的系数必为零。

∴（18-6）这就是动力学普遍方程在广义坐标中的表达式，其文字表达式为：广义力与广义惯性力相平衡。

2. 拉格朗日方程进一步研究的表达式（18-5）。

由式（18-3）得（18-7）用直接代入法可以证明下述关系式成立,（18-8）上二式称为拉格朗日关系式，它们在下面的推导中起重要作用。

第十四章 拉格朗日方程

第十四章 拉格朗日方程
FB g mBaB , FAgr mAa Ar ,
FAge mAaB ,
1）x A 0,xB 0 a Ar g sin aB cos , 2）x A 0 ,xB 0
FAgr
xB a B m Bg
mAg FBg FN
FAge aAr xA
( FAgr mg sin FAge cos )x A 0,
例14-4 质量为50kg的匀质杆,其A端与地面光滑接触以匀速2m/s 向左运动. 已知:杆长l=3m,b=1.2m,求:水平力F的大小与绳拉力 FT。 2 2 解: D vB vA n , aBn 瞬时平动: AB 0 , a B b b b aB B aB b BD , v B v A , a A 0, c n AB aB a cos300 l AB cos30 , AB aAB 对A点: mg 2 F A vB 300 2 1.28 1 / s ,
（ FBg FAge FAgr cos )xB 0, m B a B m Aa B m A g sin 2 a Ar , aB , 2 m A cos 2( m A sin mB )
例14-3 解:
调速器稳定在b时求:与b关系,弹簧原长为2l。 2e
2Fgx A 2mgy A ( m2 g F )yC 0,
定义拉氏函数：L=T-V
d (T V ) (T V ) 0, dt q j q j
V Qj , q j
d V ( ) 0, dt q j
d L L ( ) 0, dt q j q j
或: d L L ( ) Q'j , dt q j q j

拉格朗日第二类方程

拉格朗日第二类方程

A M A Q M
T 1 2 P 9Q ; ( R r )2 6 g d T 1 2 P 9Q T 2 ; (R r) 0 dt 6 g
r t 0 对定常系统，r i 中不显含时间t，即 ，于是 i/
T1 =0，T0 =0
k k 1 T T a q q 2 j j 2 j 1 1
( 6 . 1 . 6 )
故定常系统的动能是广义速度的二次齐次函数（二次型）。
由于动能恒为正，故只有当系统所有质点全部静止时动能才 有零值，因而以广义速度表示的动能的二次型是正定的。
于是：
r r i i r q i j q t j 1 j
k
( 6 . 1 . 2 )
其中 r q , r t 都是qj和t的函数 i/ j i/
系统的动能：
1 n1 2 T m r r m r i i i i i 2 2 i 1 i 1
( c )
第一项：主动力在质点系的虚位移的元功之和：
F r Q q i i j j
i 1 j 1
n
k
( d )
第二项：惯性力在质点系的虚位移的元功之和：
r i m a r m a ( qj ) i i i i i qj i 1 i 1 j 1
1n r r i i m i 2i t t 1 k n 1k k n r r r r i i i i ( m ) q q ( m ) q i j i j 2j q q q t 1 1 i 1 j 1 i 1 j j
9
式中： q 广义速度 j—

0027第二类拉格朗日方程

0027第二类拉格朗日方程

i1
i1
n
对理想约束 N i ri 0 i 1
n
(Fi miri )ri 0
i1
达朗伯-拉格朗日原理的证明
由理想约束的定义和达朗伯-拉格朗日原理：
n
n
(Fi miri)ri Niri 0
i1
i1
n
(Fi Ni miri)ri 0
i1
用约束反力代替约束后，质系就变成了自 由质系，所有虚位移都是相互独立的，故
F i N i m ir i 0 , i 1 ,2 , ,n
例1
圆轮固定于O点，不考虑圆轮在质量和摩擦。 建立系统的运动微分方程。
o y
m1
x m2
解法1 几何法
n
(Fi miri )ri 0
i1
r1 r2 a1 a2
( m 1 g m 1 a 1 ) r 1 ( m 2 g m 2 a 2 ) r 2 0
xr
C 纯滚动
x
x
O
水平面光滑
y
解
O
xr
Cx
取x和xr为广义坐标。
x
Vmgxrsin O
xr vC
x
T1 2M x21 2m(x2xr22xxrcos)1 21 2mr2x r2 r2 1 2(Mm)x24 3mxr2mxxrcos
L 1 2 (M m )x 2 4 3 m x r 2 m x x rc o s m g x rs in
T qk
qTk
qVk
Qk
V qk
V 0 qk
d dt q L k q L k 0, k1,2, ,N主的动拉力格为朗势日力方时程
L = T – V — 拉格朗日函数，或动势

传动力学第2讲_拉格朗日运动方程

传动力学第2讲_拉格朗日运动方程
（6）
动能 mV
2
2 对速度求导
是动量 mV
同理“把拉函 L 对 x 、 y 求偏导数，就与把- U 对 x 、 y 求偏导数的结果相同” ，即
L U x x
L U y y
（7）
势能对位移求导是力
通过拉函L，就把位移和速度与能量联系在一起。我们又前进了一步。
3. 拉格朗日运动方程和牛顿运动方程的数学联系
忽略摩擦内力等，则右边为 0
（10-b）
这就是本节开始所介绍的拉格朗日运动方程的表达式，Now 觉得不神秘吧，
M 0 。这里的F或M是指 说白了是ma-F=0。此式也包括转动情况，相当于 J
合力或合转矩，但不包括弹簧内部的摩擦内力等损失。 如果考虑到摩擦内力损失，上式的右边就不是0，而是体现摩擦内力的 Qx 和

m 2 y 2 U (x , y ) x 2
（5）
，势能 U 依存于 x 、 y 。把拉格朗日函数 L 对 x 求偏导数， 、y 、y 要点是：动能 T 依存于 x 求偏导数的结果相同，即 、 y 就与把动能 T 对 x L T mx x x L T my y y
-1/6-
电气传动的力学原理科普读物之二
拉格朗日运动方程
往深度里琢磨了一下：力能产生加速度，那么这个力是从哪里来的呢？无过乎就是弹簧、绳 子的拉力，这是物体变形产生的弹力；地球吸引的重力（包括斜面上的重力分量）----这是 势能。还有由速度产生冲撞的冲力，虽然属于动量和冲量的范畴，这是动能。这样一想，就 恍然大悟了，于是他把 F ma 这个公式改换为另一种写法，春雷一声震天响，一
再来看看该式的右边的
) d L d (mx dt dt x

课件：拉格朗日方程

课件：拉格朗日方程

7
第二类拉格朗日方程 几种形式
d dt
T q j
T q j
Qj
( j 1,2,, k)
1、当主动力均为有势力时
Qj
V (q1,,qk ) q j
d T dt q j
T q j
V
q j
设：L＝T-V
（拉格朗日函数）
d dt
T q j
(T V q j
)
0
2、当主动力部分为有势力时
m2g x2 x1 m1g
解： 2个自由度，取广义坐标（x1, x2） 系统的动能：
b
T
1 2
m1x12
1 2
m2 x22
1 2
J C 2
T
12（m1
m2）x12
m2 x22
x2
m2 x2 x1
r
x1
系统的势能： 以x1 =x2 =0处为零势能位置
V m1gx1 sin m2gx2 sin b
拉格朗日函数： L T V 18
3、求非有势主动力的广义力
I
vC
21
例、车厢质量为m，质心C，转动惯量 JC m，2 弹簧刚度如图 所示。水平位置为静平衡位置，建立运动微分方程。
解：系统自由度 2
广义坐标： z 静平衡位置为坐标原点
该系统外力均为有势力，
选取零势能位置：静平衡位置
系统动能： T 1 mz2 1 m 2 2
系统势能： 2
)
L z
0
mz k1(z l1 ) k2 (z l2) 0
23
mg
l 2
k 0b
0)
衡位置的伸长量有关。
拉格朗日函数: L 1 (1 ml 2 ) 2 k 2b2

拉格朗日方程

拉格朗日方程

拉格朗日函数为
L 1 m( x 2 y 2 ) 1 m(l r )22 （1）
2
2
将
L

m(l r )
和 L mr(l r )2 代入拉氏方程得质点的运动微分方
程为
积分得
(l r ) r2 0
d [(l r )] 0
V 0 , 1,2,, s
q
（2.19）
（2.18）和（2.19）式即是体系的拉格朗日平衡方程。
[例3] 求体系的平衡位置
教材：P.46 [例1]
解：体系自由度：2，广义坐标： 1 , 2
x1

l1 2
si n 1
,
y1

l1 2
cos1 ,
x2

l1
si n 1

l2 2
si n 2
,
y2

l1
cos1

l2 2
cos 2
x2

l1
si n 1

l2 2
si n 2
,
y2

l1
cos1

l2 2
第2章 拉格朗日方程
内容: • 基本概念 • 理想完整系的拉格朗日方程 • 对称性和守恒定律
重点: 完整保守系的拉格朗日方程 难点: 拉格朗日方程的推导

牛顿力学理论几乎都以力 F 为基础，因此它的应用只局限于纯力 学问题的范畴，运算也比较烦琐。18世纪伯努利、达朗贝尔、欧拉 等人发展了经典力学的分析形式。1788年拉格朗日发表了名著《分 析力学》，建立了经典力学的拉格朗日形式，用体系的动能和势能 取代了牛顿形式的加速度和力，将力学的研究和应用范围开拓到整 个物理学。

第二讲 拉格朗日定理及推论

第二讲 拉格朗日定理及推论

从而 f= +′( x0 ) f= −′( x0 ) k, 即 f= ′( x0 ) k.
数学分析 第六章 微分中值定理及其应用
高等教育出版社
那么在开区间 (a ,b)内 ( 至少 ) 存在一点ξ , 使得 f ′(ξ ) = f (b) − f (a) .
b−a
数学分析 第六章 微分中值定理及其应用
高等教育出版社
§1 拉格朗日定理和函数的单调性
罗尔定理与拉格朗日定理
函数单调性的判别
注 当 f (a) = f (b) 时,拉格朗日定理就是罗尔定理,
这就是说, f ( x) 在区间I上的任何两个值都相等, 所以为常值函数.
f (b) − f= (a) f ′(ξ )(b − a), a < ξ < b.
数学分析 第六章 微分中值定理及其应用
高等教育出版社
§1 拉格朗日定理和函数的单调性
罗尔定理与拉格朗日定理
函数单调性的判别
推论2
若函数 f 和 g均在区间I上可导,且 f ′( x) ≡ g′( x), x ∈ I ,
推论1
设 f ( x)在区间 I上的导函数 f ′( x) ≡ 0 , 则 f ( x) 在 I上是一个常值函数.
证 对于区间 I上的任何两点 x1与 x2 , x1 < x2 , f ( x) 在[x1, x2]上满足拉格朗日定理的条件, 则有
f ( x2 ) − f ( x1=) f ′(ξ )( x2 − x1 )= 0 , ξ ∈ ( x1 , x2 ).
数学分析 第六章 微分中值定理及其应用
高等教育出版社
§1 拉格朗日定理和函数的单调性
罗尔定理与拉格朗日定理
函数单调性的判别

第二章 用拉格朗日方程建立 系统数学模型

第二章 用拉格朗日方程建立 系统数学模型

第二章用拉格朗日方程建立系统的数学模型§2.1概述拉格朗日方程——属于能量法，推导中使用标量，直接对整个系统建模特点：列式简洁、考虑全面、建模容易、过程规范适合于线性系统也适合于非线性系统，适合于保守系统，也适合于非保守系统。

§2.2拉格朗日方程1．哈密尔顿原理系统总动能（2－1）系统总势能（2－2）非保守力的虚功（2－3）哈密尔顿原理的数学描述：（2－4）2．拉格朗日方程：拉格朗日方程的表达式：（2－5）（推导：）将系统总动能、总势能和非保守力的虚功的表达式代入哈密尔顿原理式中（变分驻值原理），有（2－6）利用分步积分（2－7）并注意到端点不变分（端点变分为零）（2－8）故（2－9）从而有（2－10）由变分学原理的基本引理：（设 n维向量函数M(t)，在区间内处处连续，在内具有二阶连续导数，在处为零，并对任意选取的n维向量函数，有则在整个区间内，有）我们可以得到：（2－11）即（2－12）对非保守系统，阻尼力是一种典型的非保守力，如果采用线性粘性阻尼模型，则阻尼力与广义速度成正比，在这种情况下，可引入瑞利耗散（耗能）函数D，（2－13）阻尼力产生的广义非保守力为：（2－14）对于仅受有势力和线性阻尼力作用的系统，其拉格朗日方程为：（2－15）如果系统上还作用了除有势力和阻尼力以外的非保守力，如结构受到的外激励力（对应的广义非保守力可通过非保守力的虚功求得，仍记为），则系统的拉格朗日方程为：（2－16）§2.3 拉格朗日方程在振动系统建模中应用在某些结构振动问题中，取分离体、确定各分离体的受力情况，然后利用牛顿第二定律建立方程的方法不一定可用，或者很不方便，这时，采用拉格朗日方程来建立振动方程就很方便。

1．集中参数模型中应用LuO【例】质量为M的长直杆上有一个集中质量m可在杆上滑动。

杆绕固定点摆动，建立其自由振动方程。

势能( 以O点为势能零点)动能选广义坐标为，且，代入拉格朗日方程得到：以上是对离散系统应用拉格朗日方程建立振动方程，如果利用拉格朗日方程建立连续系统的方程，则它是一种同时将系统离散化、变量分离并达到系统降阶的途径。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 2 1 2 L lv gu 2 2 u
gu
dv l gu 0 dt d 2u l 2 gu 0 dt
沿着一个弯曲 的面滑动
小结

最小作用量原理；这个世界有个最基本的原则。“能量” 偷懒原则。机械能守恒、动量取极小值。
哈密顿原理：定义了作用量能量泛函，动能-势能 拉格朗日方程也是一个原理；也可以从哈密顿原理来。
L q, q, t 的时间积分以真实运动路线上的值为驻值。
Ldt 0;
t1
t2
t2
Ldt 0
t1
t2
T V dt 0;
t1
在各种能量泛函的取值中，取驻值的那个是真实的。 最小作用量原理： 能量守恒 L V dt 0; 的情况下，动能的全变分为零；



几个理论力学的例子，挺方便的，但不是我们的目标。
拉格朗日方程漫谈
第二讲
1、怎样理解最小作用量原理？ 2、哈密顿原理； 3、拉格朗日方程的推导 4、几个理论力学的例子
中国科学院力学研究所 研究员 中国科学院大学 岗位教授
李世海 博士
最小作用量原理:



最小作用量原理（principle of least action）是物理学中描述客 观事物规律的一种方法。 从功能角度去考察和比较客体一切可能的运动（经历），认为客体的 实际运动（经历）可以由作用量求极值得出，是其中作用量最小的那 个。 自然界总是通过最短的途径发生作用的。 最小作用量原理还可详述为：对于定常保守系统，在广义坐标
t2
ab ab ab
t2
Ldt
t1
t
d L d L L u u u dt 0 dt v u dt v t1
在两个时 间端点上 q 为零
2 2 L d L L u u u dt 0 v dt v u t1 t1
qi和时间t的联合空间(q1,q2,…,qN;t)里,对于机械能E保持不
变（即δE＝0)的各条路径中,如果路径的端点（包括始点和终 点）的全变分为零,则积分
Tdt 0
t1 t2
对于真实运动的路径和邻
近的旁路比较，真实路径的积分是驻值。
机械能最小 动能最小
哈密顿原理
在N+1维空间 ( q1 , q2 ....., qN 1 , t ) 中，任两点之间连线上动势
对速度变分： 动量； 对时间求导 得到惯性项。
1 2 1 2 L mv ku 2 2
dv m ku 0 dt d 2u m 2 ku 0 dt
泛函对位移的变分：力
ku
拉格朗日方程举例：自由落体
L T V
d L L 0 dt v u
u
h
1 2 L mv mg (h u ) 2
d mv mg 0 dt dv m mg dt
hu
mg
质量乘加速度
这是一个从高度h的质量块，在重力作用下运动的方程。
拉格朗日方程举例：一条绳子沿着桌边下落
L T V
d L L 0 dt v u
t
t2
d L L dt v u udt 0 t1
t2
dt 0 dt v u
t1
d L L
d L L 0 dt v u
认识拉格朗日方程
t2 t1
哈密顿原理：是动能与势能的差的全变分为零；
拉格朗日方程：表达的更具体些。
从哈密顿原理可以得到拉格朗日方程
L L u , v, t
Ldt Ldt 0t1 t1ຫໍສະໝຸດ t2t2L
dq d L L q q v u 因为： q dt dt v u L L d d L d L v u u u v v dt dt v dt v
从基本原理得到的方程
泛函对两个函数变分
L L u , v, t
泛函：
d L L 0 dt v u
力：能量相对 位移的变化 动量：能量相 对速度的变化
L T V
对动量求时 间的导数
拉格朗日方程举例：弹簧振子
泛函的构成
L T V
d L L 0 dt v u