《理论力学 动力学》 第三讲 第二类拉格朗日方程的应用
- 格式：pdf
- 大小：280.35 KB
- 文档页数：8
下载文档原格式
合集下载
第二类拉格朗日方程适用范围
第二类拉格朗日方程适用范围
（最新版）
目录
一、引言
二、第二类拉格朗日方程的概述
三、第二类拉格朗日方程的适用范围
四、结论
正文
一、引言
拉格朗日方程是分析力学的重要方程，由约瑟夫·路易斯·拉格朗日提出，可以用来描述物体的运动，特别适用于理论物理的研究。
拉格朗日方程的功能相等于牛顿力学中的牛顿第二定律。
本文主要讨论第二类拉格朗日方程的适用范围。
二、第二类拉格朗日方程的概述
第二类拉格朗日方程是拉格朗日方程的一种，主要用于描述物体在非自由运动状态下的运动，即物体受到约束条件的运动。
第二类拉格朗日方程的形式为：δλ/δq[L/q - G/q] = 0，其中，L 表示拉格朗日量，q 表示广义坐标，G 表示广义力。
三、第二类拉格朗日方程的适用范围
第二类拉格朗日方程适用于以下情况：
1.物体受到约束条件：在实际物理系统中，物体的运动通常受到一定的约束条件，如滑动摩擦力、弹簧力等。
第二类拉格朗日方程可以用来描述物体在约束条件下的运动。
2.理论物理研究：第二类拉格朗日方程在理论物理研究中具有广泛的
应用，如在量子力学、相对论、凝聚态物理等领域。
3.工程领域：第二类拉格朗日方程在工程领域也有广泛的应用，如在机械工程、航空航天、土木工程等领域。
4.数学建模：第二类拉格朗日方程可以用来建立物体运动的数学模型，从而可以用来进行仿真和模拟。
四、结论
第二类拉格朗日方程是描述物体在约束条件下运动的重要方程，在理论物理研究、工程领域以及数学建模等方面具有广泛的应用。
拉格朗日第二类方程
拉格朗日第二类方程
拉格朗日第二类方程是经典力学中的基础概念之一。
它描述的是质点
在一定约束下的运动，是建立在尺度不变性原理的基础上的。
下面我
将按照以下列表分别介绍拉格朗日第二类方程的定义、推导过程以及
其应用。
1. 定义：
拉格朗日第二类方程是描述系统动力学的数学模型，它是由勒让德在1797年建立的，具体形式为：
d/dt (∂L/∂qᵢ) − ∂L/∂qᵢ = Qᵢ
其中，L是系统的拉格朗日函数，q是系统的广义坐标，Q是系统的非
保守力。
2. 推导过程：
拉格朗日第二类方程的推导主要分为以下几个步骤：
第一步，构建系统的拉格朗日函数，即L=T-V，其中T是系统的动能，V是系统的势能。
第二步，求出系统的广义动量pᵢ=∂L/∂qᵢ。
第三步，对广义动量求导得到系统的加速度aᵢ= d/dt (∂L/∂qᵢ)。
第四步，根据牛顿第二定律F=ma以及广义动量的定义pᵢ=∂L/∂qᵢ，将非保守力Q用广义动量表示为Qᵢ=∂V/∂qᵢ。
第五步，代入广义动量和非保守力的表达式，得到拉格朗日第二类方程d/dt (∂L/∂qᵢ) − ∂L/∂qᵢ = Qᵢ。
3. 应用：
拉格朗日第二类方程是经典力学中最基础的方程之一，它在物理学的各个领域都有广泛的应用，如
（1）陀螺的运动学研究
（2）杆的运动学研究
（3）学习简谐振动的方程
（4）学习经典电动力学中的运动方程
（5）学习光学中的光路方程等
总之，拉格朗日第二类方程在物理学研究中有着重要的地位，熟练掌握它的概念和应用对于探究自然界的规律和解决实际问题都具有重要作用。
理论力学中的拉格朗日方程
理论力学中的拉格朗日方程在理论力学中，拉格朗日方程是一种重要的数学工具，用于描述系统的运动行为和力学规律。
拉格朗日方程由意大利数学家和物理学家约瑟夫·拉格朗日于18世纪提出，被广泛应用于经典力学的各个领域。
1. 拉格朗日方程的引入拉格朗日方程的引入是为了解决在复杂的力学系统中，尤其是多体系统中，求解运动方程困难的问题。
拉格朗日方程通过引入广义坐标和广义速度的概念，将原来的N个质点受力问题转化为2N个一阶偏微分方程组的求解问题。
2. 广义坐标和广义速度在拉格朗日方程中，将系统的坐标由笛卡尔坐标系转化为广义坐标系，这样可以更好地描述系统的自由度。
广义坐标的数目等于系统的自由度，它们可以用来完全描述系统的构型。
广义速度则是对广义坐标的时间导数，表示系统的运动状态。
3. 拉格朗日量在拉格朗日力学中，拉格朗日量是一个以广义坐标、广义速度和时间为变量的函数，代表系统的能量和动力学性质。
拉格朗日量可以通过系统的动能和势能函数得到。
对于自由度为n的系统，拉格朗日量可以表示为L(q, q', t)，其中q表示广义坐标，q'表示广义速度，t表示时间。
4. 欧拉-拉格朗日方程欧拉-拉格朗日方程是拉格朗日方程的数学形式，它由拉格朗日原理引出。
欧拉-拉格朗日方程可以描述系统在运动过程中的动力学规律。
它可以表示为d/dt(dL/dq') - dL/dq = 0，其中d/dt表示对时间求导数。
通过求解这个方程组，我们可以得到系统的运动方程。
5. 应用与例子拉格朗日方程在经典力学中的应用非常广泛。
例如，它可以用于求解刚体的运动，弹性体的振动，以及受约束的质点系等问题。
通过将系统的动能和势能函数表示为广义坐标和广义速度的函数，可以得到相应的拉格朗日量，进而求解运动方程。
总结：拉格朗日方程是一种在理论力学中广泛应用的工具，用于描述系统的运动行为和力学规律。
它通过引入广义坐标和广义速度的概念，将系统的受力问题转化为求解一阶偏微分方程的问题。
拉格朗日第二类方程
代入初始条件，t =0 时， 0 0 , 0 0 得 C1 C2 0
故：
3M
gt 2
(2P9Q)( Rr)2
20
[例]图示系统，物块C质量为m1 ，均质轮A、B质量均为m2， 半径均为R，A作纯滚动，求系统的运动微分方程。 解：系统具有一自由度，保守
系统。以物块C的平衡位置为
原点，取x为广义坐标：
AF q j
（4）不含约束力。
二、保守系统的拉格朗日方程
如果作用于质点系的力是有势力，则：
Qj
V q j
而拉氏方程为：
15
d dt
T q j
T q j
V q j
由于V=V（q1，q2，...，qk），不含广义速度，所以
V q j
0,
d dt
V q j
0
上式为：
d dt
T q j
T q j
d dt
V q j
V q j
或：d dt
(T V q j
)
(T V q j
)
0
令L=T-V——拉格朗日函数
d dt
(
L q j
)
L q j
0 ( j1,2,,k )
保守系统的拉格朗日第二类方程。
16
应用拉氏方程解题的步骤：
1. 判定质点系的自由度 f，选取适宜的广义坐标。必须注意： 不能遗漏独立的坐标，也不能有多余的（不独立）坐标。
Q
A
M
T
1 2P 6
9Q (R g
r ) 2
;
d T
dt
1 2P 9Q (R r)2
6
g
;
T 0
19
理论力学-第13章 动力学普遍方程和第二类拉格朗日方程
需要指出的是，上述各式适用于任何理想、双侧约束系统， 不论约束是否完整、是否定常，也不论作用力是否有势。
*第13章 动力学普遍方程和第二类拉格朗日方程
第二类拉格朗日方程
返回
第二类拉格朗日方程
在动力学普遍方程中，由于系统存在约束，一般情形下，各 质点的虚位移并不完全独立，应用时须建立各虚位移与广义坐标 之间的关系。
第二类拉格朗日方程
N
(Qk Qk*) δ qk 0
k 1
其中Qk为对应于广义所标qk的广义力（generalized forces）; Qk*为广义惯性力（generalized inertia forces）
Qk
n i 1
Fi
ri qk
Qk*
n i 1
miai
ri qk
由于在完整约束下，δq1， δq2，…， δqN 相互独立，
Qk*
n i 1
miri
ri qk
d dt
n
(
i 1
miri
ri qk
)
n i 1
miri
d dt
( ri qk
)
d dt
n i1
mi
ri
ri qk
n i1
mi
ri
ri qk
d dt
qk
n
(
i 1
1 2
miri2 )
qk
n
(
i 1
1 2
miri2 )
d dt
(
T qk
理论力学
第3篇 工程动力学基础
第3篇 工程动力学基础
*第13章 动力学普遍方程 和第二类拉格朗日方程
*第13章 动力学普遍方程和第二类拉格朗日方程
*第13章 动力学普遍方程和第二类拉格朗日方程
第二类拉格朗日方程
返回
第二类拉格朗日方程
在动力学普遍方程中，由于系统存在约束，一般情形下，各 质点的虚位移并不完全独立，应用时须建立各虚位移与广义坐标 之间的关系。
第二类拉格朗日方程
N
(Qk Qk*) δ qk 0
k 1
其中Qk为对应于广义所标qk的广义力（generalized forces）; Qk*为广义惯性力（generalized inertia forces）
Qk
n i 1
Fi
ri qk
Qk*
n i 1
miai
ri qk
由于在完整约束下，δq1， δq2，…， δqN 相互独立，
Qk*
n i 1
miri
ri qk
d dt
n
(
i 1
miri
ri qk
)
n i 1
miri
d dt
( ri qk
)
d dt
n i1
mi
ri
ri qk
n i1
mi
ri
ri qk
d dt
qk
n
(
i 1
1 2
miri2 )
qk
n
(
i 1
1 2
miri2 )
d dt
(
T qk
理论力学
第3篇 工程动力学基础
第3篇 工程动力学基础
*第13章 动力学普遍方程 和第二类拉格朗日方程
*第13章 动力学普遍方程和第二类拉格朗日方程
理论力学：第二类拉格朗日方程的总结
θ&&(θ ) = ? x&(θ ) = ?
L中无 x, t
∂T ∂x&
=
5 2
mx& +
1 2
mLθ& cosθ
=
C
&x&(θ ) = ?
5 mx&2 + 1 mL2θ&2 + 1Lmg(1− cosθ ) = E
4
6
2
2014-3-25
8
理论力学
习题课
∂T ∂x&
2014-3-25
根据对z轴的动量矩守恒和初始条件，可得关系式： ϕ&
=
1
sin2 θ
15
理论力学
习题课
问题：B 点的运动轨迹？
θ0
=
π
4
=
0.7854,ϕ0
=
0,θ&0
=
0,ϕ&0
=
2.0rad/s
m = 1kg L = 1m k = 10N/m
∂T
∂ϕ&
=
1 mL2 3
sin2 θϕ&
=
C1
2014-3-25
mL&x&cosθ
+
1 mL2θ&&+
3
1 2
mgL sinθ
=
0
2014-3-25
10
理论力学
习题课
x
A
aA
θ&&= −15 2 g,
17L
&x&
=3g 17
求地面的约束力
F
aCt A
第二类拉格朗日方程的应用
第二类拉格朗日方程的应用
黄秋华
【期刊名称】《河池师专学报》
【年(卷),期】1991(011)003
【摘要】本文运用分析力学中的第二类拉格朗日方程,建立弹簧振子及LRC振荡电路的微分方程和计算出它们的固有周期。
【总页数】6页(P65-69,88)
【作者】黄秋华
【作者单位】无
【正文语种】中文
【中图分类】O175.1
【相关文献】
1.第二类拉格朗日方程建模在自动武器上的应用 [J], 石韬
2.基于第二类拉格朗日方程的水雷内末弹道仿真 [J], 秦锋;逢洪照
3.从动能定理到第二类拉格朗日方程 [J], 陆明万;张雄
4.动能定理与第二类拉格朗日方程推导方法 [J], 张毅
5.第二类拉格朗日方程在无初速释放动力学问题中的应用 [J], 李海龙; 刘海燕因版权原因，仅展示原文概要，查看原文内容请购买。
清华大学本校用理论力学课件8-1第二类拉格朗日方程
第 1节
第二类拉格朗日方程
2019年2月21日
广义坐标中的达伦伯-拉格朗日原理
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
理想完整约束系统：广义坐标为q1, q2, …, qN
质点i矢径： ri ri ( q1 , q2 ,
, qN , t )
n i 1
n
ri ri qk qk k 1
Qk Q 0
* k
T d Q dt qk
* k
T q k
V 如主动力都是有势力： Qk qk
d T dt qk T V q qk k
d T dt qk
T q Qk , k 1,2, k
O
y x R
R
m
L ( J mR 2 sin 2 )
d L ( J mR2 sin2 ) 2mR2 sin cos dt
例4
解
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
d L L Q dt
第 二 类 拉 格 朗 日 方 程 及 其 应 用
应用拉格朗日方程的解题步骤为 判断系统是否为完整约束，主动力是否 有势，以决定能否应用拉格朗日方程以 及应用何种形式的拉格朗日方程。 确定系统的自由度数，选择合适的广义 坐标。
按所选的广义坐标，写出系统动能、势 能或广义力。
把动能、广义力或拉格朗日函数代入拉格 朗日方程。
n n d 1 1 2 2 mi ri mi ri dt qk i 1 2 qk i 1 2
第二类拉格朗日方程
2019年2月21日
广义坐标中的达伦伯-拉格朗日原理
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
理想完整约束系统：广义坐标为q1, q2, …, qN
质点i矢径： ri ri ( q1 , q2 ,
, qN , t )
n i 1
n
ri ri qk qk k 1
Qk Q 0
* k
T d Q dt qk
* k
T q k
V 如主动力都是有势力： Qk qk
d T dt qk T V q qk k
d T dt qk
T q Qk , k 1,2, k
O
y x R
R
m
L ( J mR 2 sin 2 )
d L ( J mR2 sin2 ) 2mR2 sin cos dt
例4
解
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
d L L Q dt
第 二 类 拉 格 朗 日 方 程 及 其 应 用
应用拉格朗日方程的解题步骤为 判断系统是否为完整约束，主动力是否 有势，以决定能否应用拉格朗日方程以 及应用何种形式的拉格朗日方程。 确定系统的自由度数，选择合适的广义 坐标。
按所选的广义坐标，写出系统动能、势 能或广义力。
把动能、广义力或拉格朗日函数代入拉格 朗日方程。
n n d 1 1 2 2 mi ri mi ri dt qk i 1 2 qk i 1 2
《理论力学 动力学》 第三讲 第二类拉格朗日方程的推导
第二类拉格朗日方程曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、第二类拉格朗日方程的推导2、第二类拉格朗日方程的应用3、拉格朗日方程的初积分1、第二类拉格朗日方程的推导设由n 个质点组成的系统受m 个理想完整约束作用，系统具有N=3n-m 个自由度。
设q 1, q 2, …, q N 为系统的一组广义坐标,则每个质点的位置：12(,)(12)i i N q q q t i n =×××=×××r r ，，，，，，上式两端进行等时变分运算得到：11...i i i i N N q q t q q t d d d d ¶¶¶=+++¶¶¶r r r r 1N ikk kq q d =¶=¶år 主动力在任意虚位移上所作的虚功之和为：1δnii =×åiF r 1δNkkk Qq ==×å1、第二类拉格朗日方程的推导将以上两式代入动力学普遍方程：1()0nii iii m d =-×=åF rr &&11(δ0N nik i i k k i k Q m q q ==¶-×=¶åår r &&对于完整约束系统，广义坐标相互独立，因此δq k 是任意的，上式成立的话，恒有：0(1,2,...,)nik i i Q m k N q ¶-×==¶år r &&1、第二类拉格朗日方程的推导k Q 广义惯性力上式不便于直接应用，为此可作如下变换：(1)i i k k q q¶¶=¶¶r r &&证明：12()(12)i i N q q q t i n =×××=×××r r ，，，，，，11d d i i i ii k k q qt q q t¶¶¶==++++¶¶¶r r r r r &&&L L 注意和是广义坐标和时间的函数（不含有广义速度项），并且上式只在第k 项含有i k q ¶¶r t ¶¶ir i iq q ¶¶=¶¶r r &&k q&(2)d d i i kkt q q æö¶¶=ç÷¶¶èør r &证明：这实际是一个交换求导次序的问题12()(12)i i N q q q t i n =×××=×××r r ，，，，，，12()i i N k kq q q t q q ¶¶=¶¶r r L ，，，，对时间t 求微分1d d N ii j j kjkk q t q q q t q =æöæöæö¶¶¶¶¶=+ç÷ç÷ç÷¶¶¶¶¶èøèøèøåi r r r &221Ni j j k jk q q q q t =¶¶=+¶¶¶¶åir r &而1()N i i i j j k k j qq q q t=¶¶¶¶=+¶¶¶¶år r r &&111Ni i i i ii N j j N jq q q q q t q t =¶¶¶¶¶=+++=+¶¶¶¶¶år r r r r r &&&&L 221Ni i j j k j k q q q q t =¶¶=+¶¶¶¶år r&d d i i k kt q q æö¶¶=ç÷¶¶èør r&若函数的一阶和二阶偏导数连续12()i i N q q q t =r r L ，，，，1、第二类拉格朗日方程的推导将和代入动力学普遍方程的广义惯性力项中：i i k k q q ¶¶=¶¶r r &&d d i i kkt q q æö¶¶=ç÷¶¶èør r&1ni i i i k m q =¶×¶år r &&11d d )()d d n ni i i i i i i k k m m t q t q ==¶¶=×-׶¶åår r r r &&11d d nn i i i i i i k k m m t q q ==éù¶¶=×-×êú¶¶ëûåår rr r &&&&&11d1()d 2nni i i i i i i i k k m m t qq ==éù¶¶=×-×êú¶¶ëûåår r r r &&&&&2211d 11()()d 22nni i i i i i k km v m v t q q ==éù¶¶=-êú¶¶ëûåå&记21()ni i T m v =åd ()d k kT Tt q q ¶¶=-¶¶&1、第二类拉格朗日方程的推导将前述结果代入动力学普遍方程：11()δ0N ni k i i k k i k Q m q q ==¶-×=¶åår r &&得到d 0(12)d k k kTTQ k N t qq æö¶¶--==ç÷¶¶èøL &，，，—第二类拉格朗日方程二阶常微分方程组，方程式的数目等于质点系的自由度数。
理论力学(Ⅱ)—拉格朗日方程
B
B
解：以系统为研究对象，系统所 受的主动力有圆柱的重力。设两轮的 角加速度为 1 、 2 ，轮B质心的加速 度为 a 。假想加上惯性力，如图。
1 其中 M mR 21 2
g A
C
2
yC
1 2
mg
g MB
a
2
g FBg ma M B mR 2 2
此系统具有两个自由度，取轮A、轮B的转 角1 、 2 为广义坐标。给系统一组虚位移，如图。
q (q1 , q2 , , q N )
ri ri (q1 , q2 , , qN , t )
由动力学普遍方程，得
F δ r m a δ r 0
i 1 i i i 1 i i i
(m1 m2 ) g m1lcos
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
求：1、三棱柱后退的加速度a1； 2、圆轮质心C2相对于三棱 柱加速度ar。 解：1、分析运动 三棱柱作平动，加速度为 a1。 y D ae a1 C1
引
言
本章是将达朗伯原理和虚位移原理结合起来 推导出动力学普遍方程和拉格朗日方程。动力学 普遍方程中系统的运动是直角坐标来描述的，而 拉格朗日方程是用广义坐标来描述系统的运动， 两者都是用来解决非自由质点系的动力学问题， 它是用分析的方法解决动力学问题的出发点，因 此它是分析力学的基础。对于解决复杂的非自由 质点系的动力学问题，应用拉格朗日方程往往要 比用动力学普遍方程简便得多。
2 aC g sin 3
0
mgsin x - FIR x M IC
B
解：以系统为研究对象，系统所 受的主动力有圆柱的重力。设两轮的 角加速度为 1 、 2 ，轮B质心的加速 度为 a 。假想加上惯性力，如图。
1 其中 M mR 21 2
g A
C
2
yC
1 2
mg
g MB
a
2
g FBg ma M B mR 2 2
此系统具有两个自由度，取轮A、轮B的转 角1 、 2 为广义坐标。给系统一组虚位移，如图。
q (q1 , q2 , , q N )
ri ri (q1 , q2 , , qN , t )
由动力学普遍方程，得
F δ r m a δ r 0
i 1 i i i 1 i i i
(m1 m2 ) g m1lcos
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
求：1、三棱柱后退的加速度a1； 2、圆轮质心C2相对于三棱 柱加速度ar。 解：1、分析运动 三棱柱作平动，加速度为 a1。 y D ae a1 C1
引
言
本章是将达朗伯原理和虚位移原理结合起来 推导出动力学普遍方程和拉格朗日方程。动力学 普遍方程中系统的运动是直角坐标来描述的，而 拉格朗日方程是用广义坐标来描述系统的运动， 两者都是用来解决非自由质点系的动力学问题， 它是用分析的方法解决动力学问题的出发点，因 此它是分析力学的基础。对于解决复杂的非自由 质点系的动力学问题，应用拉格朗日方程往往要 比用动力学普遍方程简便得多。
2 aC g sin 3
0
mgsin x - FIR x M IC
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、第二类拉格朗日方程
的应用
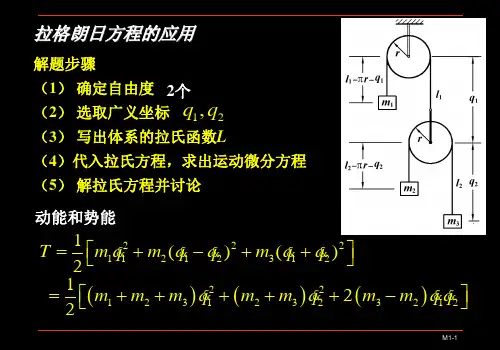
例1质量为m 1的物块C 以细绳跨过定滑轮B 联于点A, A ，B 两轮皆为均质圆盘，半径为R ，质量为m 2, 弹簧刚度为k ，质量不计。
A
C
O
x
A
O
C
x
例2已知：如图所示的运动系统中，重物M 1的质量为m 1，可沿光滑水平面移动。
摆锤M 2的质量为m 2，两个物体用长为l 的无重杆连接。
M 1
M 2
φ
C 求：此系统的运动微分方程。
2、第二类拉格朗日方程的应用
解：系统有两个自由度，选M 1的水平坐标x 1和φ为广
义坐标, 并将质点位置用广义坐标表示：
111212,0;sin ,cos x x y x x l y l j j
===-=将上式两端对时间t 求导数得：
111212,0;cos sin x x y
x x l y l j j j j ===-=-&&&&&&&&，系统的动能为:222122211()22T m x m x y =++&&&2
2212111()(2cos )22
m l m m x l x j j j =++-&&&&选质点M 2在最低处时的位置为系统的零势能位置，则系统的势能为：
)
cos 1(2j -=gl m V 系统的主动力为有势力，此为保守系统，可写出系统的动势，运用保守系统的拉格朗日方程求解，此处我们运用一般形式的第二类拉格朗日方程求解。
d 0(12)d k T T
Q k N t q q æö¶¶--==ç÷¶¶L &，，，注意：零势能位置的选取不是唯一的。
选取原则：计算方便
代入拉格朗日方程得到：
1212110()cos T T
m m x
m l x x
j j ¶¶==+-¶¶&&&，2
121221d ()()cos sin d T m m x m l m l t x j j j j
¶=+-+׶&&&&&&1
0x V Q x ¶=-=¶先计算)cos 1(2j -=gl m V 22
212111()(2cos )22
m l T m m x l x
j j j =++-&&&&2
21221sin cos T T m lx m l m
lx j j j
j j j
¶¶==-¶¶&&&&&，2
22121d ()cos sin d T m l m lx m lx t j
j j j j ¶=-+׶&&&&&&&2sin V Q m gl j j j
¶=-=-¶2
12122()cos sin 0m m x
m l m l j j j j +-+×=&&&&&(cos sin )sin 0m l l x x m gl j
j j j j -+×+=&&&&&&2、第二类拉格朗日方程的应用
x 1φ
再计算
如果质点M 2摆动很小，可以近似地认为1cos sin »»j j j ，
且可以忽略含和的高阶小量，2
j &1x
j &&微分方程可改写为:
1212()0m m x
m l j +-=&&&&1l x g j
j -=-&&
&&从以上两式中消去，得到1x
&&1210m m g
m l
j j ++=&&这是自由振动的微分方程，其通解为:)
sin(0q w j +=t A 固有角频率:
l
g
m m m 1210+=
w 摆动周期
:如果2
1m m >>则质点M 1的位移x 1将很小，
质点M 2的摆动周期将趋于普通单摆的周期
:
1lim 2m T ®¥=也可以从微分方程中消去，得到:j
&&可见质点M 1沿x 方向也作自由振动。
2、第二类拉格朗日方程的应用
这种机构又被称为椭圆摆，原因是M 1永远做水平运动，而M 1和M 2的质心C 点只能做
例3已知：均质圆轮半径为r 质量为m ，受到轻微扰动后，在半径为R 的圆弧上往复滚动，如图所示. 设表面足够粗糙，使圆轮在滚动时无滑动. 求:质心C 的运动规律
.
C
解：系统只有一个自由度，选θ为广义坐标。
系统的动能为:22
1122C T mv J w
=+2
222
111()()222R r m R r mr r q q æö-=-+×ç÷èø&&223
()4
m R r q =-&选圆弧轨道的圆心A 为零势能位置，则系统的势能为：()cos V mg R r q =--此为保守系统，系统的拉格朗日函数为：
22
3()()cos 4
L T V m R r mg R r q q
=-=-+-&代入保守系统的拉格朗日方程：d ()0d L L
t q
q ¶¶-=¶¶&得
3()2sin 0R r g q
q -+=&&与列刚体平面运动微分方程计算结果相同，
但显然此处更加简洁方便！
2、第二类拉格朗日方程的应用
利用拉格朗日方程解题的步骤及注意事项
步骤：
1、确定系统的自由度并选择合适的广义坐标；
2、利用广义坐标表示出系统的动能；
3、确定每个质点上的主动力，判断是否是保守系统；
4、对于保守系统，利用广义坐标表示系统的势能，写出系统的动势；
5、对于非保守系统，计算每个广义坐标所对应的广义力；
6、将动势或者是动能和广义力分别代入保守系统的拉格朗日方程或一般
形式的拉格朗日方程进行计算。
注意：
1、表示系统的势能时，需要选取系统的零势能位置，这个位置选取是灵
活的，需要表示的是系统相对该位置的相对势能，选取的原则是：相
对势能表示越方便、越简单越好。
2、涉及广义力的计算时，可以利用广义力的定义计算，也可以利用广义
虚位移的任意性进行计算，保守系统还可以通过势能函数对广义坐标
的偏导数来计算。