刚体平面运动习题
- 格式:doc
- 大小:311.50 KB
- 文档页数:7

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A += (2) α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R =ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为hv AC v AP v ABθθω2000cos cos ===6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:R v R v A A ==ωR v R v B B 22==ω B A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度=12 rad/s ,=30,=60,BC =270mm 。




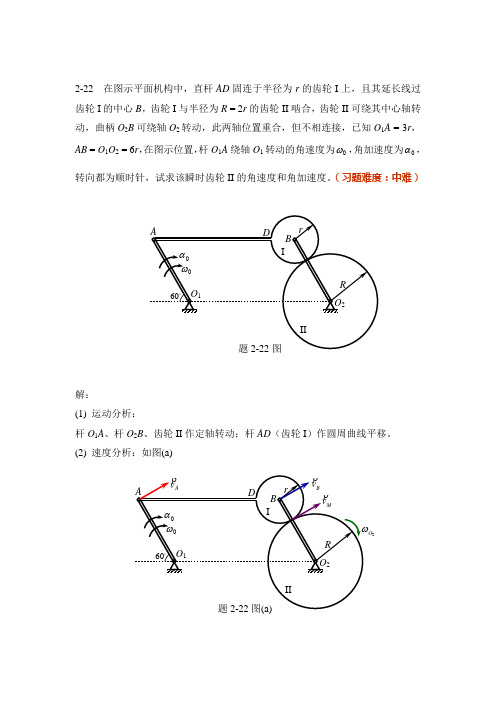
2-22 在图示平面机构中,直杆AD 固连于半径为r 的齿轮I 上,且其延长线过齿轮I 的中心B ,齿轮I 与半径为R = 2r 的齿轮II 啮合,齿轮II 可绕其中心轴转动,曲柄O 2B 可绕轴O 2转动,此两轴位置重合,但不相连接,已知O 1A = 3r ,AB = O 1O 2 = 6r ,在图示位置,杆O 1A 绕轴O 1转动的角速度为0ω,角加速度为0α,转向都为顺时针,试求该瞬时齿轮II 的角速度和角加速度。
(习题难度:中难)解:(1) 运动分析:杆O 1A 、杆O 2B 、齿轮II 作定轴转动;杆AD (齿轮I )作圆周曲线平移。
(2) 速度分析:如图(a)2O假设齿轮I 上点M '和齿轮II 上点M ''相啮合,则M M v v '''= ,且tt M M a a '''= 。
杆O 1A :0013ωωr A O v A =⋅=(A O 1⊥)杆AD (齿轮I ):A B v v = 03ωr v v A B ==(B O 2⊥) 03ωr v v B M =='(B O 2⊥) 齿轮II(3) 加速度分析:如图(b)杆O 1A : 2n 3ωr a A =(1//) 0t 3αr a A =(A O 1⊥) 杆AD (齿轮I ):A B a a = 20n n 3ωr a a A B ==(2//BO ) 0tt 3αr a a A B ==(B O 2⊥)tn t n M M B B B M a a a a a a '''+=+==齿轮I 上M '点:0tt 3αr a a B M =='(B O 2⊥) 齿轮II : 0t t t 3αr a a a B M M ==='''(注意:齿轮啮合点的切向加速度相同,但是齿轮啮合点的法向加速度并不相同。
刚体平面运动一、是非题(正确或是用√,错误或否用×,填入括号内。
)1. 刚体的平动和定轴转动均是刚体平面运动的特例。
( √ )2. 刚体作瞬时平动时,刚体的角速度和角加速度在该瞬时一定都等于零。
( × )3. 轮子作平面运动时,如轮上与地面接触点C 的速度不等于零,即相对地面有滑动,则此时轮子一定不存在瞬时速度中心。
( × )4. 若在作平面运动的刚体上选择不同的点作为基点时,则刚体绕不同基点转动的角速度是不同的。
( × )5. 某刚体作平面运动,若A 和B 是其平面图形上的任意两点,则速度投影定理[][]AB B AB A v v =永远成立。
( √ )6. 作平面运动的刚体,某瞬时若角速度、角加速度同时为零,则此时刚体上各点的速度与加速度均相等。
( √ )7. 接上题,在上述条件下,有结论:刚体作平动。
( × )8. 设A 为平面运动刚体上的任意一点,I 为刚体在某时刻的速度瞬心,则A 点的运动轨迹在此处的曲率半径等于A 、I 间的距离。
( × )9. 我们知道,作平面运动的刚体上任意两点A 、B 之间有相对速度,因此,如果将一坐标系固定在此刚体上,在此坐标系中所观察到的A 、B 点之速度一般来说不相等。
( × )10. 刚体作平面运动时,若某瞬时其上有二点加速度相同,则此瞬时刚体上各点的速度都相同。
( √ )11. 平面图形上任意两点的速度在任一直线上的投影始终相等。
( × )12. 平面图形瞬时平动时,其上任意两点的加速度在这两点连线上的投影相等。
( √ )13. 刚体平动必为刚体平面运动的特例,但刚体定轴转动不一定是刚体平面运动的特例。
( × )14. 请判断下述说法是否正确:A. 刚体的平动是平面运动的特殊情况。
( × )B. 刚体的平面运动是平动的特殊情况。
( × )C. 刚体的定轴转动是平面运动的特殊情况。
第8章 刚体平面运动习题
1.是非题(对画√,错画×)
8-1.刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动。
( ) 8-2.平面图形的运动可以看成是随着基点的平移和绕基点的转动的合成.( ) 8-3.平面图形上任意两点的速度在某固定轴上投影相等。
( ) 8-4.平面图形随着基点平移的速度和加速度与基点的选择有关。
( ) 8-5.平面图形绕基点转动的角速度和角加速度与基点的选择有关。
( ) 8-6.速度瞬心点处的速度为零,加速度也为零。
( ) 8-7.刚体的平移也是平面运动。
( ) 2.填空题(把正确的答案写在横线上)
8-8.在平直轨道作纯滚动的圆轮,与地面接触点的速度为 。
8-9.平面图形上任意两点的速度在 上投影相等。
8-10.某瞬时刚体作平移,其角速度为 ;刚体上各点速度 ;各点加速度 。
3.简答题
8-11.确定图示平面运动物体的速度瞬心位置。
题8-11图
(a) (b)
(c)
8-12.若刚体作平面运动,下面平面图形上A 、B 的速度方向正确吗? 题8-12图
(a) (b) (c)
8-13.下面图形中O 1A 和AC 的速度分布对吗?
8-14.圆轮做曲线滚动,某瞬时轮心的速度o v 和加速度o a ,轮的半径为R ,则轮心的角
加速度等于多少?速度瞬心点处的加速度大小和方向如何确定?
题8-13图
B
8-15.用基点法求平面图形个点的加速度时,为什么没有科氏加速度? 4.计算题
8-16.椭圆规尺AB 由曲柄OC 带动,曲柄以匀角速度o ω绕O 轴转动,如图所示,若取C 为基点,OC=BC=AC=r ,试求椭圆规尺AB 的平面运动方程。
8-17.半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动,如图所示。
曲柄以匀角加速度α绕O
轴转动,设初始时角速度0=ω、角加速度0=α、转角0=ϕ,若选动齿轮的轮心C 点为基点,试求动齿轮的平面运动方程。
题8-16图
题8-17图
8-18.曲柄连杆机构,已知OA =40cm ,连杆AB =1m ,曲柄OA 绕O 轴以转速180=n r/min 匀速转动,如图所示。
试求当曲柄OA 与水平线成o 45角时,连杆AB 的角速度和中点M 的速度大小。
8-19.已知曲柄OA =r ,杆BC=2r ,曲柄OA 以匀角速度4rad/s =ω顺时针转动,如图所示。
试求在图示瞬时点B 的速度以及杆BC 的角速度。
题8-18图
题8-19图
B
8-20.如图所示筛料机,由曲柄OA 带动筛子BC 摆动。
已知曲柄OA 以转速40=n r/min 匀速转动,OA =0.3m ,当筛子BC 运动到与点O 在同一水平线时,o BAO 90=∠,摆杆与水平线夹角为060时,试求在图示瞬时筛子BC 的速度。
8-21.如图所示四连杆机构,曲柄OA 以匀角速度绕O 轴转动,当曲柄OA 处于水平位
置时,曲柄O 1B 恰好在铅锤位置。
设OA =O 1B=AB 2
1
=l ,试求和曲柄O 1B 的角速度。
题8-20图
A
题8-21图
A
1
8-22.如图所示平面机构,曲柄OA 以匀角速度o ω绕O 轴转动,并带动连杆AB 使圆轮在地面作纯滚动,圆轮的半径为R ,在图示瞬时曲柄OA 与连杆AB 垂直,曲柄OA 与水平线的夹角为060角,OA =r ,试求该瞬时圆轮的角速度。
8-23.如图所示的曲柄连杆机构中,连杆AB 的中点C 以铰链与杆CD 相连,而杆CD 又与杆DE 相连,杆DE 绕E 轴转动,已知曲柄OA 以角速度8rad/s =ω绕O 轴转动,OA =25cm ,DE =100cm ,当B 、E 两点在同一铅垂线上时,O 、A 、B 三点共线,且o CDE 90=∠,试求杆DE 的角速度。
题8-22图
题8-23图
8-24.如图所示的平面机构中,曲柄OA =r ,以匀角速度o ω绕O 轴转动,连杆CD =6r ,在图示瞬时与铅垂线成o α30=角,杆DE 、AB 处于水平位置,试求点D 的速度和连杆CD 的角速度。
8-25.如图所示的平面机构中,已知OA =BD=DE =0.1m ,310.EF =m ;曲柄OA 以角速度4rad/s =ω绕O 轴转动,在图示瞬时曲柄OA 与水平线OB 垂直,且B 、D 、F 在同一铅垂线上,又DE 垂直于EF 。
试求杆EF 的角速度和点F 的速度。
题8-24图
题8-25图
A
8-26.如图所示的瓦特行星齿轮机构中,平衡杆O 1A 绕O 1轴转动,并借连杆AB 带动曲OB ;而曲柄OB 活动地装在O 轴上。
在O 轴上装有齿轮Ⅰ,齿轮Ⅱ与连杆AB 固连于一体。
已知33021.r r ==m ,O 1A=0.75m ,AB=1.5m ,平衡杆的角速度6rad/s =ω,试求当o 60=γ且o 90=β时,曲柄OB 和齿轮Ⅰ的角速度。
8-27.如图所示齿轮Ⅰ在齿轮Ⅱ内滚动,其半径分别为r 和R=2r 。
曲柄1OO 绕O 轴以等角速度o ω转动,并带动行星齿轮Ⅰ。
试求轮Ⅰ速度瞬心P 点的加速度。
题8-26图
I
题8-27图
8-28.半径为r 的圆柱体在半径为R 的圆弧内作无滑动的滚动,如图所示,圆柱中心C 的速度为c v ,切向加速度为τc a ,试求圆柱的最低点A 和最高点B 的加速度。
8-29.曲柄OA 以匀角速度2rad/s =ω绕O 轴转动,,并借连杆AB 驱动半径为r 的轮子在半径为R 的圆弧内作无滑动的滚动。
设OA=AB=R=2r=1m ,试求图示瞬时轮子上的点B 、C 的速度和加速度。
题8-28图
题8-29图
8-30.如图所示的平面机构中,曲柄OA =r ,以匀角速度o ω绕O 轴转动,AB=6r ,r BC 33=,试求图示瞬时,滑块C 的速度和加速度。
8-31.如图所示曲柄OA =20cm 绕O 轴以匀角速度rad/s 01=ω转动,并借连杆AB 带动滑块B 沿铅直滑道运动,AB=100cm ,当曲柄OA 与连杆AB 相互垂直并与水平线的夹角分别为o α45=、o β45=时,试求此瞬时连杆AB 的角速度、角加速度以及滑块B 的加速度。
题8-30图
题8-30图
8-32.在曲柄齿轮椭圆规中,齿轮A 和曲柄O 1A 固结为一体,齿轮C 和齿轮A 半径均为
r 并互相啮合,如图所示。
已知AB=21O O ,4021.B O A O ==m ,A O 1以匀角速度rad/s 20.ω=绕O 1轴转动。
M 为轮C 上的点,CM =0.1m 。
图示瞬时,CM 为铅直,试求此瞬时点M 的
速度和加速度。
8-33.圆轮在平直的轨道上作纯滚动,图示瞬时点O 在铰C 的正下方,连杆OA 在水平的导轨中运动,其速度为v =1.5m/s ,o 30=θ,并带动摇杆CD 绕点C 转动,轮的半径为R =100mm ,OC=200mm ,试求摇杆CD 的角速度。
题8-32图
题8-33图
8-34.如图所示,轮O 在水平面上滚动,而不滑动,轮心以匀速v o =0.2m/s 运动,轮缘上固连销钉B ,此销钉在摇杆O 1A 的槽内滑动,并带动摇杆绕O 1轴转动。
已知轮的半径R =0.5m ,图示瞬时O 1A 是轮的切线,摇杆与水平线的夹角为060,试求此瞬时摇杆O 1A 角速度和角加速度。
8-35.平面机构的曲柄OA 长为2l ,以匀角速度o ω绕O 轴转动。
图示瞬时AB=BO ,并且o OAD 90=∠,试求此瞬时套筒D 相对于杆BC 的速度和加速度。
题8-34图
题8-35图
8-36.如图所示曲柄导杆机构,曲柄OA=120mm ,OB =160mm ,图示瞬时o AOB 90=∠。
曲柄以角速度rad/s 4=ω,角加速度2rad/s 2=α绕O 轴转动。
试求此瞬时导杆AC 的角加速度以及导杆相对于套筒B 的加速度。
8-37.图示机构中,曲柄O 1A 以匀角速度ω绕O 1轴转动。
已知O 1A=r ,图(a )、(b)、(c)中,l=4r ,图(d)中l=2r ,试求图示瞬时水平杆的速度和加速度。
ωα
C
题8-37图
(c)
(d)
(a) (b)
题8-36图。