理论力学课后习题答案 第6章 刚体的平面运动分析(2020年7月整理).pdf

第六章 分析力学滔滔长江东逝水，浪花淘尽英雄。

达朗贝尔，拉格朗日，哈密顿等许多前贤相聚于此“力学论剑”，其“冲击波”使非线性问题也不攻自破。

长江后浪推前浪，你或许在此能够加倍“忘乎因此‘。

微分方程将叱咤风云。

[要点分析与总结]1虚功原理：（平稳时）理想条件下，力学系的平稳条件是各质 点上的主动力所作的虚功之和为零：10ni i i W F r δδ==•=∑用广义坐标来表述：310n ii i x W F q q ααδδ=∂==∂∑ 2达朗贝尔原理（动力学下的虚功原理）： 1()0ni i i i i W F m r r δδ==-•=∑〈析〉r δ，W δ均是在时刻未转变（0dt =）时所假想的量，而广义坐标a q 能够是角度，长度或其它的独立的坐标变量。

3拉格朗日方程()d T TQ dt q q ααα∂∂-=∂∂ (1,2,3,,)a s =在保守力下，取拉氏数 L T V =-方程为：()0d L L dt q q αα∂∂-=∂∂ 假设拉氏数中L 不显含广义坐标q β，那么：0Lq β∂=∂ 即 循环积分： Lp const q ββ∂==∂ 4微振动非线性系统在小角度近似下，对拉氏方程的应用 5哈密顿函数与正那么方程 （1） 哈密顿函数1(,,)sH p q t L p q ααα==-+∑式中T Lp q q ααα∂∂==∂∂为广义坐标动量 （2） 正那么方程Hq P Hp q H Lt tαααα∂=∂∂=-∂∂∂=-∂∂ (1,2,3,,)a s =假设哈氏函数H 中不显含广义坐标q β，那么：0Hp q ββ∂=-=∂ 即：循环积分 Tp const q ββ∂==∂ 在稳固条件下（H 中不显含t ），12sp q T ααα==∑那么有能量积分：H T V =+6泊松括号1[,]()sG H G HG H q p p q ααααα=∂∂∂∂=-∂∂∂∂∑ 7哈密顿原理与正那么变换 （1）哈密顿原理保守力系下：210t t Ldt δ=⎰概念：21t t S Ldt =⎰为主函数（3） 正那么变换通过某种变数的变换，找到新的函数*H ，使正那么方程的形式不变（相当于坐标变换）。

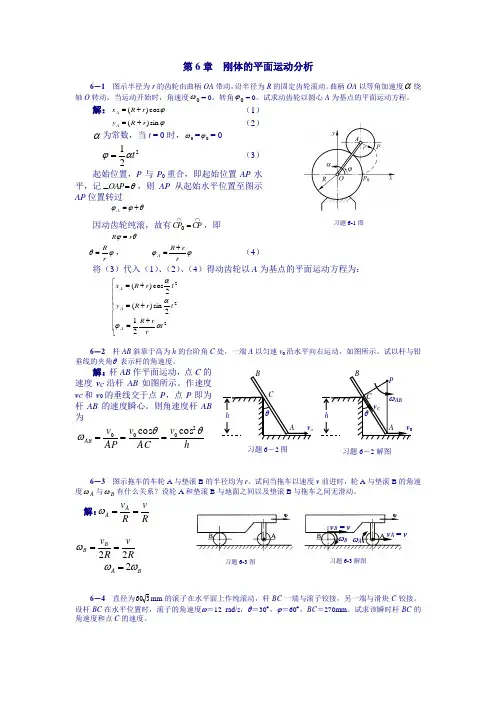
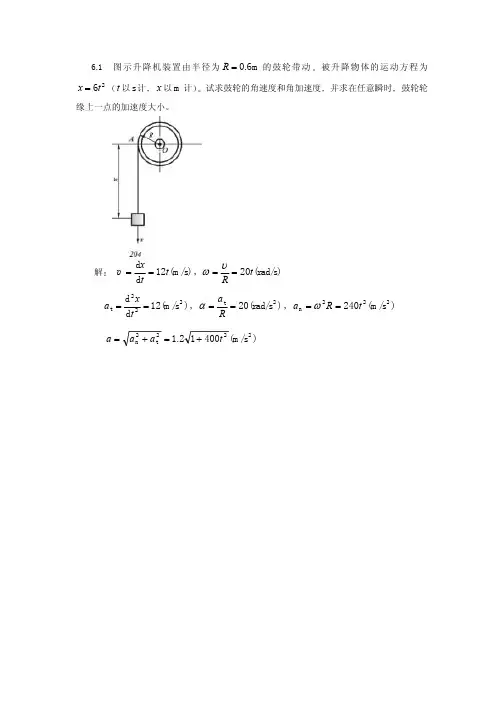
第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。

试求动齿轮以圆心A 为基点的平面运动方程。

解：ϕcos )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。

试以杆与铅垂线的夹角θ 表示杆的角速度。

解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。

作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。

则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。

试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。

解：RvR v A A ==ωR v R v B B 22==ωB A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。

设杆BC 在水平位置时，滚子的角速度ω＝12 rad/s ，θ＝30︒，ϕ＝60︒，BC ＝270mm 。

试求该瞬时杆BC 的角速度和点C 的速度。

hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6－2图PωABv CABCv ohθ习题6－2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解：杆BC 的瞬心在点P ，滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6－5 在下列机构中，那些构件做平面运动，画出它们图示位置的速度瞬心。

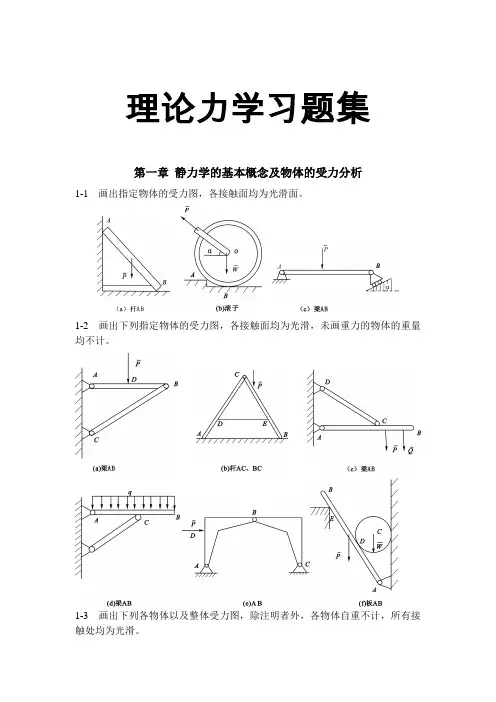
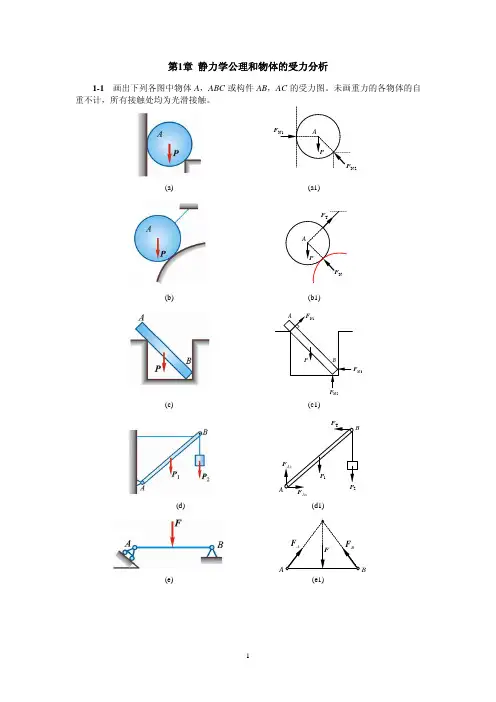
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图，各接触面均为光滑面。

1-2 画出下列指定物体的受力图，各接触面均为光滑，未画重力的物体的重量均不计。

1-3 画出下列各物体以及整体受力图，除注明者外，各物体自重不计，所有接触处均为光滑。

(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在铰车D 上，如图所示。

转动铰车，物体便能升起，设滑轮的大小及滑轮转轴处的摩擦忽略不计，A、B、C三处均为铰链连接。

当物体处于平衡状态时，试求拉杆AB和支杆CB所受的力。

2-2 用一组绳悬挂重P=1kN的物体，求各绳的拉力。

2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN，P2=800kN及制动力T=193kN，桥墩自重W=5280kN，风力Q=140kN。

各力作用线位置如图所示，求将这些力向基底截面中心O简化的结果，如能简化为一合力，试求出合力作用线的位置。

2-4 水平梁的支承和载荷如图所示，试求出图中A、B处的约束反力。

2-5 在图示结构计算简图中，已知q=15kN/m，求A、B、C处的约束力。

2-6 图示平面结构，自重不计，由AB、BD、DFE三杆铰接组成，已知：P=50kN，M=40kN·m，q=20kN/m，L=2m，试求固定端A的反力。

图2-6 图2-72-7 求图示多跨静定梁的支座反力。

2-8 图示结构中各杆自重不计，D、E处为铰链，B、C为链杆约束，A为固定端，已知：q G=1kN/m，q=1kN/m，M=2kN·m，L1=3m，L2=2m，试求A、B、C 处约束反力。

图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成，O、B处为铰链，A、E是固定铰支座，尺寸如图，已知：r=20cm，在滑轮上吊有重Q=1000N的物体，杆及轮重均不计，试求支座A和E以及AO杆上的O处约束反力。

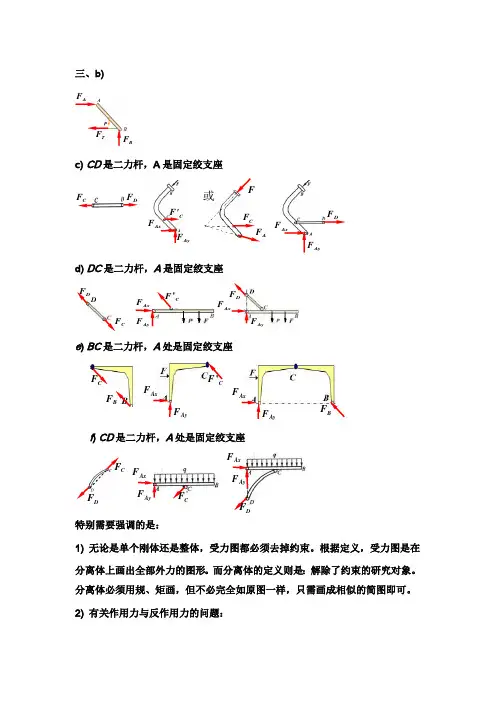
三、b)c) CD 是二力杆，A 是固定绞支座d) DC 是二力杆，A 是固定绞支座e ) BC 是二力杆，A 处是固定绞支座f ) CD 是二力杆，A 处是固定绞支座特别需要强调的是：1) 无论是单个刚体还是整体，受力图都必须去掉约束。

根据定义，受力图是在分离体上画出全部外力的图形。

而分离体的定义则是：解除了约束的研究对象。

分离体必须用规、矩画，但不必完全如原图一样，只需画成相似的简图即可。

2) 有关作用力与反作用力的问题：AyF Ax F 'C F CDF AyF AxF DF CF BFAyF AxF CF 'AyF AxF BF CF 'AyF Ax F DF AyF AxF DF CF AF FCF 或AyF AxF C 'F AyF AxF DF DF CF AF B F TFa ) 习惯上，先找出二力杆，并标示一约束反力(如F D ，将其认为是作用力)。

在另一受力图上的相联点(如D 点)，然后根据作用力与反作用力定律确定的约束反力当作反作用力，标示为F'D 。

其中，符号 ' 是为了表示它是F D 的反作用力。

所以，它是有确切含义的。

标注符号时，要注意先后顺序，先确定的约束反力不标注 ' 符号，后确定的约束反力一定要标注符号 ' 。

两者必须成对、反向画。

b ) 为了明确地表示两者的作用力与反作用力关系，两个力的下脚标必须一致，如上述的D 。

不能随手写其它符号，以免产生误解。

下脚标通常用该点的符号表示，不宜象中学物理中那样，标示成数字。

3) 整体受力图一般最后画，整体受力图上的约束反力，应该与各单个刚体上已经画出的约束反力方向一致，以免产生岐义。

一、b ) k 点是光滑面约束，A 是光滑铰链，B 、O 是固定铰支座。

c ) 先确定斜杆(标注为DE )是二力杆，A 是固定绞支座，B 是可动绞支座。

BC 杆带铰，C 铰与AC 杆上C 孔铰接，力F 作用在铰上。

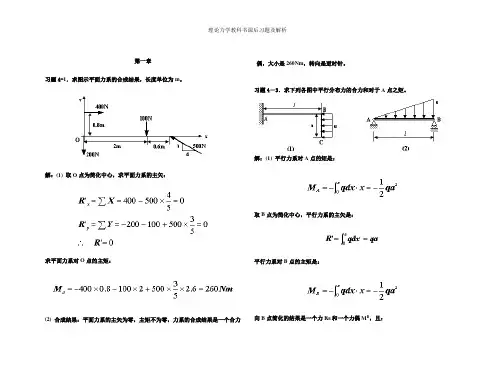
第一章习题4-1．求图示平面力系的合成结果，长度单位为m。

解：(1) 取O点为简化中心，求平面力系的主矢：求平面力系对O点的主矩：(2) 合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力偶，大小是260Nm，转向是逆时针。

习题4－3．求下列各图中平行分布力的合力和对于A点之矩。

解：(1) 平行力系对A点的矩是：取B点为简化中心，平行力系的主矢是：平行力系对B点的主矩是：向B点简化的结果是一个力R B和一个力偶M B，且：如图所示；将R B向下平移一段距离d，使满足：最后简化为一个力R，大小等于R B。

其几何意义是：R的大小等于载荷分布的矩形面积，作用点通过矩形的形心。

(2) 取A点为简化中心，平行力系的主矢是：平行力系对A点的主矩是：向A点简化的结果是一个力R A和一个力偶M A，且：如图所示；将R A向右平移一段距离d，使满足：最后简化为一个力R，大小等于R A。

其几何意义是：R的大小等于载荷分布的三角形面积，作用点通过三角形的形心。

习题4-4．求下列各梁和刚架的支座反力，长度单位为m。

解：(1) 研究AB杆，受力分析，画受力图：列平衡方程：解方程组：反力的实际方向如图示。

校核：结果正确。

(2) 研究AB杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。

校核：结果正确。

(3) 研究ABC，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。

校核：结果正确。

习题4-5．重物悬挂如图，已知G=1.8kN，其他重量不计；求铰链A的约束反力和杆BC所受的力。

解：(1) 研究整体，受力分析（BC是二力杆），画受力图：列平衡方程：解方程组：反力的实际方向如图示。

习题4-8．图示钻井架，G=177kN，铅垂荷载P=1350kN，风荷载q=1.5kN/m，水平力F=50kN；求支座A的约束反力和撑杆CD所受的力。

理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

8-1 图示四杆机构1OABO 中，AB B O OA 211==；曲柄OA 的角速度s rad /3=ω。

求当090=ϕ而曲柄B O 1重合于1OO 的延长线上时，杆AB 和曲柄B O 1的角速度。

参考答案：因OA 杆作定轴转动，故OA v A ⋅=ω。

AB 杆做平面运动其速度瞬心为O 点，s rad OAv AAB /3===ωω，而OA OB v AB B ⋅=⋅=ωω3， 所以s rad s rad BO OAB O v B B O /2.5/3333111≈==⋅==ωωω（逆时针）8-2 四连杆机构中，连杆AB 上固联一块三角板 ABD 。

机构由曲柄A O 1带动。

已知：曲柄的角速度s rad A O /21=ω；曲柄cm A O 101=，水平距离cm O O 521=；AD=5cm ,当A O 1铅垂时，AB 平行于21O O ，且AD 与1AO 在同一直线上；角030=ϕ。

求三角板ABD 的角速度和D 点的速度。

参考答案：三角板 ABD C ，由此可得：s rad ctg O O AO AO AC v A O A/07.121111=⋅+⋅==ϕωωs cm CD v D /35.25=⋅=ω8-7 如图所示，在振动机构中，筛子的摆动由曲柄连杆机构所带动。

已知曲柄OA 的转速cm OA r n 30min,/40==。

当筛子BC 运动到与点O 在同一水平线上时，090=∠BAO ，求此瞬时筛子BC 的速度。

解：由图示机构知BC 作平行移动，图示位置时，B v 与CBO 夹角为30°，与AB 夹角为60°。

Av Bv Dv Av CωAv Bv由题意知 m/s π40.030.03040π=⨯⨯=⋅=OA v A ω 由速度投影定理 AB B AB A v v )()(= 得 ︒=60cos B A v vm/s 2.51π8.060cos ==︒==AB BC v v v8-6 图示机构中，已知cm EF cm DE cm BD cm OA 310,10,10,10==== OA ωs rad /4=，在图示位置，曲柄OA 与水平线OB 垂直，且B 、D 和F 在同一铅直线上。

6－1在图示四连杆机构中，已知：匀角速度O ω，OA =B O 1=r 。

试求在°=45ϕ且AB ⊥B O 1的图示瞬时，连杆AB 的角速度AB ω及B 点的速度。

解：连杆AB 作平面运动，由基点法得BA A B v v v +=由速度合成的矢量关系，知φcos v A BA =v杆AB 的角速度)(/AB /O BA AB 2122+==ωωv （逆时针）B 点的速度2245/r cos v O A B ω=°=v （方向沿AB ）6－2. 在图示四连杆机构中，已知：3.021===L B O OA m ，匀角速度2=ωrad/s 。

在图示瞬时，11==L OB m ，且杆OA 铅直、B O 1水平。

试求该瞬时杆B O 1的角速度和角加速度。

解：一．求1ω60230..OA v A =×=⋅=ω m/s取A 为基点，则有BA A B v v v += 得 23.0/6.0ctg v v A B ===ϕ m/sm09.2)3.01()3.0/6.0(sin /v v 2/122A BA =+×==ϕ杆B O 1的角速度67630211../BO /v B ===ω rad/s 顺时针 二．求1ε取点A 为基点，则有n BA A a a a a a ++=+ττBA nB B将上式向X 轴投影21222857s /m .B O /ctg v )sin AB /v (OA ctg a )sin /a (a a a sin a cos a sin a BBA n B n BA A B nBA A n B B +=⋅+⋅+⋅−=++−=−=+−ϕϕωϕϕϕϕϕττ杆B O 1的角加速度7.1923.0/8.57/11===B O a B τεrad/s 2逆时针6－3.图示机构中，已知：OA =0.1m ， DE =0.1m ，m 31.0=EF ，D 距OB 线为h=0.1m ；rad 4=OA ω。