静定桁架课堂练习 结构力学 哈工大
- 格式:ppt
- 大小:1.04 MB
- 文档页数:7

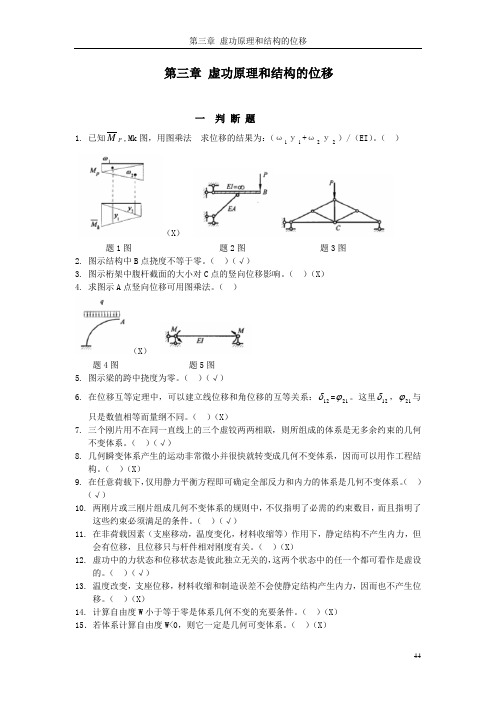
第三章 虚功原理和结构的位移一 判 断 题1. 已知P M ,Mk 图,用图乘法 求位移的结果为:(ω1у1+ω2у2)/(EI )。
( ) (X ) 题1图 题2图 题3图2. 图示结构中B 点挠度不等于零。
( )(√)3. 图示桁架中腹杆截面的大小对C 点的竖向位移影响。
( )(X )4. 求图示A 点竖向位移可用图乘法。
( )(X )题4图 题5图5. 图示梁的跨中挠度为零。
( )(√)6. 在位移互等定理中,可以建立线位移和角位移的互等关系:12δ=21ϕ。
这里12δ,21ϕ与只是数值相等而量纲不同。
( )(X )7. 三个刚片用不在同一直线上的三个虚铰两两相联,则所组成的体系是无多余约束的几何不变体系。
( )(√)8. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
( )(X )9. 在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
( )(√)10. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
( )(√)11. 在非荷载因素(支座移动,温度变化,材料收缩等)作用下,静定结构不产生内力,但会有位移,且位移只与杆件相对刚度有关。
( )(X )12. 虚功中的力状态和位移状态是彼此独立无关的,这两个状态中的任一个都可看作是虚设的。
( )(√)13. 温度改变,支座位移,材料收缩和制造误差不会使静定结构产生内力,因而也不产生位移。
( )(X )14. 计算自由度W 小于等于零是体系几何不变的充要条件。
( )(X )15.若体系计算自由度W<0,则它一定是几何可变体系。
( )(X )16.平面几何不变体系的三个基本组成规则是可以相互沟通的。
( )(√)17.三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
( )(X )18.图示三铰刚架,EI 为常数,A 铰无竖向位移。




5-1 用静力法作图示梁的支杆反力F N1、F N2、F N3及力M K 、F Q K 、F N K 的影响线。
解:取隔离体如图(a)所示∑M A =0F N3 = 52l (x−32l)∑F x =0F N1 =F N2∑F y = 0F N1 = 52 (4−x l )x<3l 时取隔离体如图(e)所示M K = F N3lF Q K =−F N3F N K =0x >3l 时取隔离体如图(f)所示M K = F N3l −1×(x−3l)=−x+l8 2F Q K =1−F N3 = − x5 5lF N K =0由求出的影响系数方程可作出影响线如图所示。
5-2 用静力法作图示梁的F By 、M A 、M K 和F Q K 的影响线。
解:取隔离体如图(a)所示∑F y =0F By =1∑M B =0M A =x x <l/2时, 取隔离体如图(f)所示M K =l/2F Q K =−1x >l/2时, 取隔离体如图(e)所示M K =l −xF Q K =0由影响系数方程可作出影响线如图所示。
5-3 用静力法作图示斜梁的F Ay、F Ax、F By 、M C 、F Q C 和F N C 的影响线。
(1)解:∑M A =0F By = x/l∑F y =0F Ay =1−x/l∑F x =0F Ax =0x<a,取右侧∑M c =0 M C= bx/l∑F r =0 F Q C =−x l cosα∑Fβ=0 F N C = x l sinαx>a,取左侧∑M c =0 M C = a(1−x/l)∑F r =0 F Q C = (1−x l )cosαx ∑Fβ=0 F N C =−(1−l )sinα由影响系数方程可作出影响线如图所示。
5-3(2)解:∑M A =0F By = x l tanαx∑F y = 0F Ay =− l tanα∑F x =0 F Ax =−1x<a,取右侧∑M c =0 M C = b l x tanα∑F r =0 F Q C =−x l sinα∑Fβ= 0 F N C = x l sinα⋅tanαx>a,取左侧∑M c =0 M C = tanα⋅a(1−x/l)∑F r =0 F Q C = sinα−x l sinα∑Fβ= 0 F N C = cosα+ x l tanα⋅sinα由影响系数方程可作出影响线如图所示。
第七章影响线一判断题1. 图示梁AB与A0B0,其截面C与C0弯矩影响线和剪力影响线完全相同。
(X)题1图题2图2. 图示结构Q E影响线的AC段纵标不为零。
(X)3. 图示梁K截面的M K影响线、Q K影响线形状如图a、b所示。
4. 图示梁的M C影响线、Q C影响线形状如图a、b所示。
5. 图示梁的M C影响线、M B影响线形状如图a、b所示。
第七章影响线6. 图示结构M B影响线的AB段纵标为零。
7. 图示梁跨中C截面弯矩影响线的物理意义是荷载P=1作用在截面C的弯矩图形。
(X)8. 用静力法作静定结构某量值的影响线与用机动法作该结构同一量值的影响线是不等价的。
(X)9. 求某量值影响线方程的方法,与恒载作用下计算该量值的方法在原理上是相同的。
(√)10. 影响线是用于解决活载作用下结构的计算问题,它不能用于恒载作用下的计算。
(X)11. 移动荷载是指大小,指向不变,作用位置不断变化的荷载,所以不是静力荷载。
(X)12. 用静力法作影响线,影响线方程中的变量x代表截面位置的横坐标。
(X)13. 表示单位移动荷载作用下某指定截面的内力变化规律的图形称为内力影响线。
(√)14. 简支梁跨中截面弯矩的影响线与跨中有集中力P时的M图相同。
(X)15. 简支梁跨中C截面剪力影响线在C截面处有突变。
(√)16. 绝对最大弯矩是移动荷载下梁的各截面上最大的弯矩。
(√)17. 静定结构及超静定结构的内力影响线都是由直线组成。
(X)18. 图示结构Q C影响线的CD段为斜直线。
19. 图示结构K断面的剪力影响线如图b所示。
(√)题19图20. 用机动法作得图a所示Q B左结构影响线如图b。
题20图题21图21. 图示结构a杆的内力影响线如图b所示22. 荷载处于某一最不利位置时,按梁内各截面得弯矩值竖标画出得图形,称为简支梁的弯矩包络图。
(X)23. 单位力P=1沿图a所示桁架上移动,杆K内力影响线如图b.第七章影响线24. 图为图所示结构Q C右的影响线。
第一章平面体系的几何组成分析一判断题1. 图示体系是几何不变体系。
(×)题1图题2图题3图题4图2. 图示体系为几何可变体系。
(×)3. 图示体系是几何不变体系。
(×)4. 图示体系是几何不变体系。
(√)5. 图示体系是几何不变体系。
(×)题5图题6图题19图题20图6. 图示体系为几何不变有多余约束。
(×)7. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
(×)8. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
(√)9. 在任意荷载下,仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
(√)10. 计算自由度W小于等于零是体系几何不变的充要条件。
(×)11. 几何可变体系在任何荷载作用下都不能平衡。
(×)12. 三个刚片由三个铰相联的体系一定是静定结构。
(×)13. 有多余约束的体系一定是超静定结构。
(×)14. 有些体系为几何可变体系但却有多余约束存在。
(√)15. 平面几何不变体系的三个基本组成规则是可以相互沟通的。
(√)16. 三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
(×)17. 两刚片用汇交于一点的三根链杆相联,可组成几何不变体系。
(×)18. 若体系计算自由度W<0,则它一定是几何可变体系。
(×)19. 在图示体系中,去掉其中任意两根支座链杆后,所余下都是几何不变的。
(×)20. 图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
(×)21. 有多余约束的体系一定是几何不变体系。
(×)22. 几何不变体系的计算自由度一定等于零。
(×)23. 几何瞬变体系的计算自由度一定等于零。
(×)24. 图中链杆1和2的交点O可视为虚铰。
静定桁架结构的内力分析——典型例题【例1】求如图1(a)所示桁架中所有杆件的轴力。
图1【解】(1)取截面Ⅰ-Ⅰ以右部分作研究,由有:,解得:从而有:(2)再依次由结点8、4、3、7、6、5、1的平衡条件,求得其它杆轴力,如图1(b)所示。
【例2】求如图2所示桁架中杆件a 、b 的轴力。
图2【解】经几何组成分析,此结构为三铰桁架。
(1)求支座反力取铰7右边部分为隔离体分析,由有:10M =∑89230x F d F d F d ⨯-⨯-⨯=892x F F=892)3N F F d ==拉力70M =∑22x y F F =由整体平衡条件有:从而有: , 再分别由整体平衡条件、有:, (2)作截面Ⅰ-Ⅰ,取左边作为隔离体研究,由得:(3)作截面Ⅱ-Ⅱ,取右边作为隔离体研究,由有:,解得: 从而得:。
【例3】求如图3所示桁架中杆件a 、b 的轴力。
图3【解】经几何组成分析,此结构为主从结构,截面Ⅰ-Ⅰ左边为附属部分,右边为基本部分。
杆件58、78为零杆。
(1)作截面Ⅰ-Ⅰ,取左边作为隔离体研究,由得:10M =∑2224x y F d F d F d ⨯+⨯=⨯()223x F F =←()223y F F =↑0x F =∑0y F =∑()123x F F =→()113y F F =↑0y F =∑()13Na F F =-压力80M =∑222xb x y F d F d F d ⨯+⨯=⨯23xb F F =-()Nb F =压力0y F =∑()1V F F =↑由整体平衡条件得 ,由有 (2)作截面Ⅱ-Ⅱ,取右边作为隔离体研究研究 由有:,从而得: 由有:,从而得:【例4】求如图5-7所示桁架中杆件a 、b 的轴力。
图4【解】(1)取截面Ⅰ-Ⅰ以上部分为隔离体分析,由有:,从而得:(2)取截面Ⅱ-Ⅱ以左部分为隔离体,由有:,从而得:【例5】求如图5(a)所示桁架中杆件a 、b 的轴力。