结构力学李廉锟版-静定平面桁架全解
- 格式:ppt
- 大小:4.55 MB
- 文档页数:80

第5章静定平面桁架复习思考题1.桁架的计算简图作了哪些假设?它与实际的桁架有哪些差别?答:(1)桁架的计算简图假设①各结点都是无摩擦的理想铰;②各杆轴都是直线,并在同一平面内且通过铰的中心;③荷载只作用在结点上并在桁架的平面内。
(2)桁架的计算简图与实际桁架的差别①结点的刚性。
②各杆轴线不可能绝对平直,在结点处也不可能准确交于一点。
③非结点荷载(例如杆件自重、风荷载等)。
④结构的空间作用,等等。
2.如何根据桁架的几何构造特点来选择计算顺序?答:根据桁架的几何构造特点来选择计算顺序的方法(1)找出零杆根据节点的几何特征和外部受力特点判断出零杆。
(2)选择合适的方法求解桁架①用节点法解简单桁架时,在求出支座反力后,可按与几何组成相反的顺序,从最后的结点开始,依次倒算回去,便能顺利地用结点法求出所有杆件的内力。
②求解联合桁架时,用结点法将会遇到未知力超过两个的结点,可以先用截面法将联合杆件的内力求出,再用结点法求解其它杆件的内力。
③求解复杂桁架时,根据桁架的几何构造特点看,可先算出截面单杆的内力,再选择合适的计算方法求解剩余杆的内力。
3.在结点法和截面法中,怎样尽量避免解联立方程?答:在结点法和截面法中,尽量避免解联立方程的方法:(1)采用结点法时,为避免解联立方程,可改选投影轴方向或者改用力矩平衡方程(向力的汇交点取矩)。
(2)采用截面法时,使用力矩法的关键在于选取合理的力矩中心,因此应尽量选取多力汇交点作为力矩中心;使用投影法的过程中,应尽量选择多个力所在方向作为力分解的坐标轴。
4.零杆既然不受力,为何在实际结构中不把它去掉?答:在实际结构中不把零杆去掉的原因:(1)在实际结构中,工况更复杂,荷载不是一成不变的,荷载改变后,“零杆”可能变为非零杆。
因此,为了保证结构的几何形状在任何载荷作用下都不会改变,零杆不能从桁架中除去。
(2)在理想桁架(做了诸多假设)中“零杆”才是零杆,而实际结构中,零杆的内力也不是零,只是较小而已。


第3章 静定梁与静定刚架
3.1 复习笔记【知识框架】
【重点难点归纳】
一、单跨静定梁 ★★★★
1.内力
表3-1-1 内力的基本概念
图3-1-1
图3-1-22.内力与外力间的微分关系及积分关系(1)由平衡条件导出的微分关系式
计算简图如图3-1-3所示,微分关系式为
(Ⅰ)
d d d d d d s
s N
F q x
x M F
x F p x
x ⎧=⎪⎪⎪=
⎨⎪⎪=-⎪⎩-()()
图3-1-3
(2)荷载与内力之间的积分关系
如图3-1-4
所示,结合式(Ⅰ)可得梁的内力积分公式,积分公式及其几何意义见表3-1-2。
图3-1-4
表3-1-2 内力的积分公式及几何意义
3.叠加法作弯矩图
表3-1-3 常用叠加法及其作图步骤
图3-1-5
图3-1-6
二、多跨静定梁 ★★★★
多跨静定梁是由构造单元(如简支梁、悬臂梁)多次搭接而成的几何不变体系,其计算简图见图3-1-7,几何构造、计算原则、传力关系见表3-1-4。
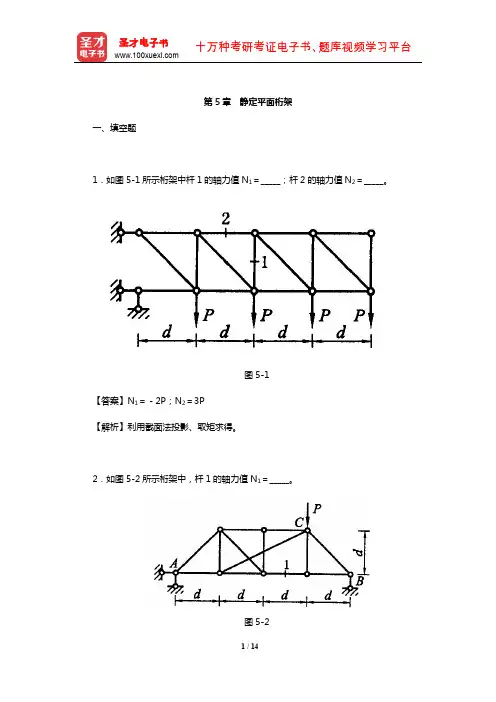
第5章静定平面桁架一、填空题1.如图5-1所示桁架中杆1的轴力值N1=_____;杆2的轴力值N2=_____。
图5-1【答案】N1=-2P;N2=3P【解析】利用截面法投影、取矩求得。
2.如图5-2所示桁架中,杆1的轴力值N1=_____。
图5-2【答案】【解析】先以A点取矩求得B处支座反力,再利用截面法取矩求杆1轴力。
3.如图5-3所示结构中,杆1的轴力值N1=_____;杆2的轴力值N2=_____。
图5-3【答案】N1=P;N2=-2P【解析】取上半部分分析,对右上角的结点取矩得出N2,再求出支座反力即可求出N1。
二、判断题1.如图5-4所示桁架中杆1的轴力为1kN。
()图5-4【答案】对【解析】用截面法、取矩。
2.如图5-5所示桁架中杆1的轴力为零。
()图5-5【答案】对【解析】左右支座竖向反力均为向上的P,用截面法,由∑Y=0即可得出。
3.如图5-6所示桁架中杆1的轴力为P。
()图5-6 【答案】错【解析】反对称荷载,对称杆轴为零。
4.如图5-7所示桁架中杆1的轴力为2P。
()图5-7 【答案】错【解析】截面法,三、选择题1.如图5-8所示桁架中零杆(含零支杆)个数为()。
A.0根B.1根C.2根D.3根图5-8【答案】D【解析】利用对称性可知,水平支杆和内部的两根杆为零杆。
2.如图5-9所示桁架中杆1的轴力值N1为()。
A.-pB.-2pC.D.-1.414p图5-9【答案】C【解析】先结点A后结点B,两次用结点法可求得。
3.如图5-10所示结构中杆1的轴力值N0为()。
A.0B.1.414PC.-1.414PD.0.707P图5-10。