当前位置：文档之家 › 1-2自然坐标系

1-2自然坐标系

  • 格式：pdf
  • 大小：984.74 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

自然坐标系

自然坐标系

r

t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a

an

v2 R


vB

B vA
R

O
A
大小，方向，作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er

ds dt
er


ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动， 法向加速度
v vB
vA

v vB
vA
Δv vB vA ,

AB R
lim lim ar
t 0
则：a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略：
（1）分析问题特点，建立恰当的坐标系 （2）由运动方程求解速度随时间变化的表达式 （3）分别计算出切向加速度与法向加速度，再 求解合加速度的大小和方向
解：根据加速度的定义：
ar
anern
a er

v2 R
ern

dv dt
er
a an2 a 2
v

ds dt
2
R
a

d
dt
1.2t

工程力学-弧坐标系中研究点的运动

工程力学-弧坐标系中研究点的运动
v vt s 2RAcost
y
O
v
an
O1
a
M at
M0
B x
at v s 2R2 Asin t
an
v2
4R2 2 A2
R
cos2 t
4R 2 A2
cos2 t
v 2RAcostet
a at an
12
例1.4 半径r的车轮在直线轨道上纯滚动(滚而不滑)， 已知轮心A的速度为常矢量 u ，求轮缘上一点M
的轨迹、速度、加速度、轨迹曲率半径。
y
Au
根据纯滚动的条件： 轮心A的坐标：
M
xA=OC= MC=ut
O
C
x 轮子转过的角度：
= MC/r = ut / r= xA/ r 即 xA r
选择 为广义坐标（也可选xA）。
点M运
xM
OC r sin
ut r sin ut r
动方程
yM
AC r cos
vB ——B点的速度
38
rB
O
B
vBA
B
rrABvAvABAvABvA以B BvvB为vvABA基A关以(点3A于)两为((21v基)点)指Bv点ABv速A向(BBA的的度与相方大关对向的小系于：转：式A垂向的vvB直一BA速=于致度vAA。)A B应B连v注B线A意，中：
vBA表示以A为基点时B点相对于
(1.15)
et
eb
en
en
lim
S0 S
d dS
(1.17)
可视为副法线 eb 绕切线 et 的转角
5
已知对单位矢量 a ：
da d a
对自然轴系的活动标架，有：

1-2马克思主义自然观的形成与发展(系统自然观)

1-2马克思主义自然观的形成与发展(系统自然观)

• 著名物理学家玻尔兹曼(Ludwig Boltzmann， 1844-1906) 1886年在皇家科学院的一次讲演中直 截了当地宣告：“如果你要问我 截了当地宣告： 如果你要问我，我们的世纪是 我们的世纪是 钢铁世纪、蒸汽世纪，还是电气世纪，那么我会 毫不犹豫地回答 我们的世纪是机械自然观的世 毫不犹豫地回答，我们的世纪是机械自然观的世种 坚信化学元素之间 定有某种秩序各种 元素周期表：被认为彼此孤立、无关的元素 成为内在联系的统一整体。
1.2机械唯物主义自然观的方法论危机
• 恩格斯指出 恩格斯指出，18世纪末以后，经验自然科学积累 世纪末以后 经验自然科学积累 了如此庞大数量的确实的知识材料，以至于在每 一个研究领域中 都不可避免地出现把这些材料 一个研究领域中，都不可避免地出现把这些材料 有系统地和依据其内在联系加以整理的要求。 • 观察、实验、归纳和演绎等经验方法远不够，必 观察 实验 归纳和演绎等经验方法远不够 必 须重视理论方法 • 分析方法有局限 有 • 比较、假说等思维方法获得了较大发展
4、辩证唯物主义自然观的作用
• 是对古希腊有机论自然观和机械论自然观的 扬弃 • 它消除了神秘主义、神创论、目的论、物种 它消除了神秘主义 神创论 目的论 物种 不变论的自然观 • 批判了自然依赖于外部作用而运动的观点， 指出了机械唯物论的某些不足之处，是具有 革命性、科学性特点的自然观。 • 辩证自然观不是人类自然观的终结，辩证自 然观也没有终结机械论自然观
（2）挽救以太的尝试和经典物理学的努力
• 1892年爱尔兰物理学家菲兹杰拉德（George FitzGerald，1851-1901）对迈克耳逊—莫雷实验 的零结果提出了一种新奇的解释：物体在以太风 中的收缩假说。 • 他认为在运动方向上，物体长度将会缩短，包括 他认为在运动方向上 物体长度将会缩短 包括 一切可能的测量装置以及人的感官在内，都以同 样的方式相应地收缩 以致我们无法在光学实验 样的方式相应地收缩，以致我们无法在光学实验 中探测出以太漂移的迹象。

2第二讲自然坐标系圆周运动的角量描述

2第二讲自然坐标系圆周运动的角量描述
dx
vx
u
dt
dy
gt
vy
dt
v u2 g 2 t 2
2
g
t
dv d
2
2 2

u g t
a
dt dt
u2 g 2 t 2
an a a
2
ug
2
u g t
2
2 2
相对运动
球
垂
直
往
返
运动具有相对性
球作曲线运动
如何变换？
描述运动三参量合成的约定
绝对量
建立自然坐标系：（P的切向）（P的法向）
p
o
ˆ
n̂
规定：切向单位矢量 ˆ ， 指向运动方向
法向单位矢量 n̂
指向轨道的凹侧
用这样一对正交的切向、法向单位矢量构成坐
标系统称为自然坐标系。
在自然坐标系中，切向、法向单位矢量并不固
定，它们随质点的位置而变。
p
ˆ
o
ˆ
n̂
n̂
直角坐标系是静坐标系
教学基本要求：
能计算质点在平面内运动时的速度和加速度；
能计算质点作圆周运动时的角速度、角加速度
、切向加速度和法向加速度。
本节内容提纲
一，自然坐标系
1，运动方程
2，速度
3，加速度
二，圆周运动的角量描述
1，角位置
2，角速度
3，角加速度
三，角量与线量的关系
四，一般曲线运动
一、自然坐标系中的运动方程，速度及加速度表示：

=

‫ ׬‬tgα


=


−

tgα

自然坐标圆周运动相对运动

自然坐标圆周运动相对运动
《关于两门新科学的对话和数学证明对话集》 一书，总结了他的科学思想以及在物理学和天文学 方面的研究成果。
伽利略所取得的巨大成就，开创了近代物理学 的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
（1）位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略（Galileo Galilei，1564—1642）
伽利略杰出的意大利物理学家和 天文学家，实验物理学的先驱者。
他提出著名的相对性原理、惯性 原理、抛体的运动定律、摆振动的等 时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结：自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变 化的快慢
反映速度方向变 化的快慢程度
dv a dt
an
v2
aa
a 2 an 2

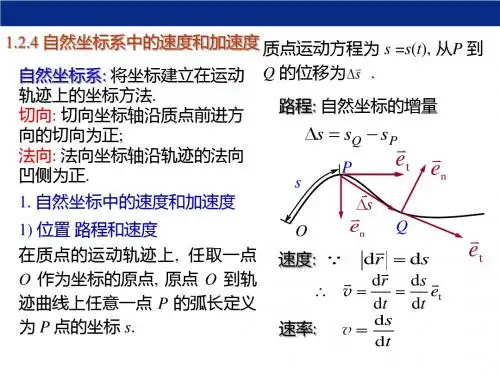
2 自然坐标系 圆周运动 相对运动

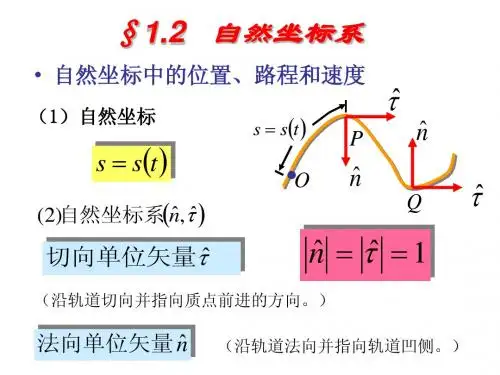
2 自然坐标系 圆周运动 相对运动

(3) 匀变速率圆周运动基本公 式的角量表示
0 t
1 2 2 2 0 2 0
(1) 一般圆周运动
0 0 t t 2
dv at dt
at 0
v2 an R
(2) 匀速圆周运动
与匀变速直线运动基本公式 的数学形式相同.

总加速度
a a t an
改变 改变 速度方向
速度大小
dv et 切向加速度 at at et dt
法向加速度 总加速度
v2 an en
at
an

et

a a t an
改变
讨论: (1) at = 0 匀速率运动; at≠ 0 变速运动. (2) an = 0 直线运动; an≠ 0 曲线运动 例1-7. 抛体运动 y u0
y = u0 sina t -
自然坐标:
du at dt a a a
2 2 t 2 n
1 2 gt 2 u2 an
a at
an
A g
g sin g cos
2 v0 gcos
B g
C
g

0 g
2 v0 cos2 g
g sin g cos
2 v0 gcos
ag
相对速度 牵连速度 注意: 暗含两个参考系时间与空 绝对速度 （风对地） （风对人） （人对地） 间测量的绝对性(绝对时空观).
aOP aOP aOO
例1-9. 某人骑自行车以速率 v0向 东行驶.有风以同样的速率由北偏 西 30方向吹来.问: 人感到风是 从那个方向吹来？
a
vax vab v xb

质点运动学

质点运动学

r ∆r = ∆r r ∆s = ∆r
r ∆ r = ∆r
∆s = ∆r
r ∆s = ∆ r
质点的运动学方程为x=6+3t-5t3(SI),判断正误 判断正误: 质点的运动学方程为 判断正误 质点作匀加速直线运动，加速度为正。 质点作匀加速直线运动，加速度为正。 质点作匀加速直线运动，加速度为负。 质点作匀加速直线运动，加速度为负。 质点作变加速直线运动，加速度为正。 质点作变加速直线运动，加速度为正。 质点作变加速直线运动，加速度为负。 质点作变加速直线运动，加速度为负。
Y
1.角位移
t时刻 P点 角位置θ
P′ ω (t + ∆t ) ω (t ) R ∆θ P
t＋∆t时刻 P′点 角位置θ + ∆θ
角位移
顺时针为负 ∆θ 逆时针为正
θ
s
X
O
2.角速度
平均角速度：
∆θ dθ = ds = v 瞬时角速度（角速度）： ω＝ lim = Rdt R ∆t →0 ∆t dt 角速度方向： 右手螺旋，四指指向质点旋转方向，则大拇指 表示角速度方向。
Z
r r r ∆v d v d 2 r r a = l im = = 2 ∆ t → 0 ∆t dt dt
p1
r v1 ( t )
•
r dvx r dv y r dvz r r r • r a = ax i + a y j + az k = i+ j+ k r r r1 dt dt dt r2 d 2x r d 2 y r d 2z r = 2i + 2 j+ 2k dt dt dt
r v = | v |=
v +v +v =

自然坐标系

自然坐标系
dv a dt
v 2 (t ) an R
ˆ v v(t )
3 一般平面曲线运动
dv v 2 a n dt
曲线变化缓慢大 曲线变化急大
详细推导
ˆ v v
ˆ dv dv d ˆ a v dt dt dt

ˆ d的大小为 d 1
• 随质点一起运动，自然变换位置和方向。
举例：圆周运动 1 匀速圆周运动 速度 大小：v=衡量
ˆ n
ˆ
方向：切向
ˆ v v
v ˆ ˆ a an n n R
2
a 加速度 大小： n v / R
2
方向：指向圆心
2 变速率圆周运动 速度 加速度
ˆ ˆ a a an a an n
dv a dt 2 v an

a
a a
a 2 an 2
2 2 2
dv v dt
a tg an

加速度总是指向曲线的凹侧，因为正是加速 度的法向分量改变了质点的运动方向。
1.3 角量描述
v2 B v1
§1.2 自然坐标系
• 自然坐标中的位置、路程和速度
（1）自然坐标
s st
ˆ
s st
ˆ ˆ (2) 自然坐标系n,
P
ˆ n
Q
O
ˆ n
ˆ
ˆ 切向单位矢量
ˆ ˆ n 1
（沿轨道法向并指向轨道凹侧。）
（沿轨道切向并指向质点前进的方向。）
ˆ 法向单位矢量 n
自然坐标的特点
ˆ 方向为n
dˆ d d dr v ˆ ˆ ˆ ˆ n n n n dt dt dt dt

01-2自然坐标系中的描述及相对运动

01-2自然坐标系中的描述及相对运动

(1) a 0 匀速率运动； a 0 变速率运动
(2) an 0 直线运动; an
0
曲线运动
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
例1.由楼窗口以水平初速度v0射出一发子弹，取枪 口为原点，沿v0为x轴，竖直向下为y轴，并取发射 时t=0.试求： (1)子弹在任一时刻t的位置坐标及轨道方程； (2)子弹在t时刻的速度，切向加速度和法向加速度。

C
v2
法向加速度大小等于速率平方除以曲率半径， 方向沿轨道的法线指向。
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
dv v a a an n dt
a a
2
a an

a
a an
2 2 2
2
2 v dv dt
2 2
相对性：参照系、坐标系
直角坐标
22Leabharlann 2222
x
x
x
x
x
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
2-1. 在自然坐标中描述质点的运动
1. 位置：在轨道上取一固定点O，用质点距离O的路程
长度 s，可唯一确定质点的位置。位置 s有正负之分
2. 位置变化: s 3. 速度： 沿切线方向。
解：(1) x v0 t
2
1 2 y gt 2
o
v0
x

1 x g y 2 2 v0
an
y g
a
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
(2) v x v0 , v y gt
o
2 0 2 2

直角坐标系极坐标系自然坐标系的定义

直角坐标系极坐标系自然坐标系的定义

直角坐标系、极坐标系和自然坐标系的定义在数学和物理学中，直角坐标系、极坐标系和自然坐标系是描述空间中点的位置和关系的工具。

它们各自具有不同的特点和应用场景。

本文将介绍这三种坐标系的定义及其基本特点。

直角坐标系直角坐标系，又称笛卡尔坐标系，是最为常见和基础的坐标系。

它由两条彼此垂直的坐标轴组成，通常为x轴和y轴，并以原点作为坐标轴的交点。

直角坐标系中的点的位置可以用两个数值表示，即横坐标x和纵坐标y。

这两个数值分别表示点在x轴和y轴上的投影长度。

在直角坐标系中，任意两点之间的距离可以通过勾股定理计算。

直角坐标系在几何学、物理学、计算机科学等领域被广泛应用。

它可以方便地描述平面上的几何图形，同时也可以用于描述三维空间中的物体位置。

极坐标系极坐标系是一种二维坐标系，它由一个原点和一个极轴组成。

与直角坐标系不同的是，极坐标系使用极径和极角来表示点的位置。

极径表示点与原点的距离，而极角表示点与极轴的夹角。

在极坐标系中，点的位置可以通过一个有序对(r, θ)表示。

其中，r为极径，θ为极角。

极径可以为正或者负，而极角通常在范围[0, 2π)内取值。

极坐标系可以方便地描述围绕原点的对称性，例如圆形、花瓣状和螺旋形的几何图形。

此外，在天文学、物理学、工程学等领域，极坐标系也具有独特的应用。

例如，描述天体运动中的角度和距离，以及雷达中的目标定位等。

自然坐标系自然坐标系是一种用于描述曲线、曲面等的坐标系。

它的特点是将点的位置表示为离散对象沿曲线或曲面的位置参数。

自然坐标系中的坐标值通常为0到1之间的数值，表示点在曲线或曲面上的相对位置。

自然坐标系的引用点通常选择为曲线或曲面上具有特殊含义的点，例如极值点、交点或重心等。

通过自然坐标系，可以用简洁的方式描述和计算曲线或曲面上的各种性质和变化。

自然坐标系在计算机图形学、有限元分析、仿真等领域被广泛应用。

例如，可以使用自然坐标系来表示二维和三维几何图形中的点、线和面，以及描述物体的形变和变形等。

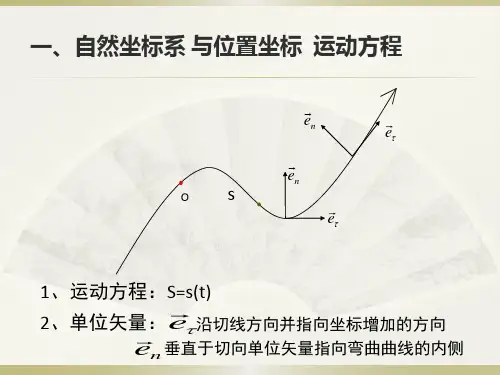
自然坐标系

自然坐标系
系下的加速度
1. 匀速圆周运动， 法向加速度
v vB
vA
v vB
vA
Δv vB vA ,
AB R
lim lim a
t 0
t
t 0
AB .
t R
en
v2 R
en
法向加速度
a
an
v2 R
vB
B vA
R
O
A
大小，方向，作用
2. 一般圆周运动的
切向加速度和法向加速度
ds dt
e
3、自然坐标系下的加速度：a
anen
a e
v2 R
en
dv dt
e
a a n 为法向加速度 为切向加速度
vA
a
d
dt
切向加速度的方向为切线方向 它反映了速度大小的变化, 作用是改变质点的速度大小.
an a
a
a
an2 a2
2
R
2
d
dt
2
a
tg a
an
arctg a ,
an
a an2 a2
an
例题：汽车在半径为200m的圆弧形公路上刹车，刹
车开始阶段的运动方程为 s 20t 0.2t3（单位：m,s）
tg an
a
12233'
总结解题策略：
（1）分析问题特点，建立恰当的坐标系 （2）由运动方程求解速度随时间变化的表达式 （3）分别计算出切向加速度与法向加速度，再 求解合加速度的大小和方向
小结本节内容：
1、自然坐标系下的运动方程及其单位矢量：
S=s(t) en e
2、自然坐标系下的速度：
v
分析方法

地形图的坐标表示方式

地形图的坐标表示方式

１、地形图坐标‎系：我国的地形‎图采用高斯‎－克吕格平面‎直角坐标系‎。

在该坐标系‎中，横轴：赤道，用Ｙ表示；赤道以南为‎负，以北为正；纵轴：中央经线，用Ｘ表示；中央经线以‎东为正，以西为负。

坐标原点：中央经线与‎赤道的交点‎，用Ｏ表示。

我国位于北‎半球，故纵坐标均‎为正值，但为避免中‎央经度线以‎西为负值的‎情况，将坐标纵轴‎西移５００‎公里。

２、北京５４坐‎标系：１９５４年‎我国在北京‎设立了大地‎坐标原点，采用克拉索‎夫斯基椭球‎体，依此计算出‎来的各大地‎控制点的坐‎标，称为北京５‎４坐标系。

３、ＧＳ８４坐‎标系：即世界通用‎的经纬度坐‎标系。

４、６度带、３度带、中央经线。

我国采用６‎度分带和３‎度分带：１∶２．５万及１∶５万的地形‎图采用６度‎分带投影，即经差为６‎度，从零度子午‎线开始，自西向东每‎个经差６度‎为一投影带‎，全球共分６‎０个带，用１，２，３，４，５，……表示．即东经０～６度为第一‎带，其中央经线‎的经度为东‎经３度，东经６～１２度为第‎二带，其中央经线‎的经度为９‎度。

１∶１万的地形‎图采用３度‎分带，从东经１．５度的经线‎开始，每隔３度为‎一带，用１，２，３，……表示，全球共划分‎１２０个投‎影带，即东经１．５～４．５度为第１‎带，其中央经线‎的经度为东‎经３度，东经４．５～７．５度为第２‎带，其中央经线‎的经度为东‎经６度．地形图上公‎里网横坐标‎前２位就是‎带号，例如：河北省１：５万地形图‎上的横坐标‎为２０３４‎５４８６，其中２０即‎为带号，３４５４８‎６为横坐标‎值。

在分层设色‎地形图中,绿色表示的‎地形是A高‎原B平原C‎山地D盆地‎一.什么是地图‎地图是按一‎定的数学法‎则和综合法‎则，以形象－符号表达制‎图物体(现象)的地理分布‎、组合和相互‎联系及其在‎时间中的变‎化的空间模‎型，它是地理信‎息的载体，又是信息传‎递的通道。

二.地图制图学‎及其理论基‎础地图制图学‎属地球科学‎中的一门学‎科。

《自然坐标系》课件

《自然坐标系》课件

自然坐标系的定义
基本概念
• 不同于常规的笛卡尔坐标系、极坐标 系、球坐标系
• 能够更准确地表达物体的真实形状、 大小和位置
特点
• 包含坐标与方位信息 • 内站洼凸性自动转化 • 合理的分带分区结构 • 与国际通用地图厂商软件兼容
自然坐标系的计算方法
点坐标的计算方法 距离的计算方法
根据已知坐标和对应的偏角和距离，可得 出所求点的坐标
自然坐标系
本PPT课件将介绍自然坐标系的基本概念、应用场景及计算方法，以及它在地 图制作和工程设计中的具体应用。希望这份课件能为您带来全新的体验。
相关概念
直角坐标系
由x,y构成的平面直角坐标系
极坐标系
以某点为原点，以该点到直线的距离和该点与极轴正方向的夹角表示平面上其它点的坐标。
球坐标系
将空间点的位置用径向距离r、极角θ、方位角φ这三个参数来表示的坐标系。
国际上常用的大比例尺地图所采用的坐标系统 是自然坐标系。
工程设计
在公路、铁路、港口等大型工程和建筑物的设 计建造中，自然坐标系被广泛用于数据管理和 信息加工。
总结
1 优缺点
2 发展前景
自然坐标系能够更准确地表达物体的真 实形状、大小和位置，但是其计算方法 相对较为繁琐。
在大数据处理和智能交通等领域的应用 逐渐增多，自然坐标系的应用将更加广 泛。
根据正反算公式和高斯投影的方式，通过 计算两点之间的投影距离，得出两点间的 实际距离
自然坐标系的转换
1
自然坐标系和直角坐标系之间的转换
通过正反算公式将自然坐标系的坐标转换为直角坐标系的坐标，间的转换
按一定的方式将自然坐标系转换为极坐标系。
自然坐标系的应用
地图制作

坐标系分类

坐标系分类
2
2、造型坐标系
造型坐标系（MCS：Modeling Coordinate System） 是右手坐标系。它是用来描述世界坐标系中每个具体物体的 形状，每个物体均由其自身的造型坐标系定义。
造型坐标系 局部坐标系 世界坐标系 整体坐标系。
3、观察坐标系
观察坐标系（VCS：View Coordinate System）是为了 将三维物体投影到显示屏幕（观察平面）上而建立起来的， 是左手坐标系。

一、点与字符的裁剪 点的裁剪比较简单，当图形系统的窗口确定之后，
设被裁剪的点的坐标为（x，y），则只有当该点的坐标
满足下式
该点才位于窗口之内，并经过窗口-视图变换后送视 区中显示，否则该点位于窗口之外而被舍去。
16
字符的裁剪，根据裁剪精度不同，可分为三种情况。 如图所示。 （1）字串裁剪
用一个限界矩形来包含整个文本字符串，判断该限界矩 形是否全部位于裁剪窗口的内部，如果是，则字符串全部 保留，如果不是，则字符串全部不可见。这是字符裁剪的 最简单方法，裁剪速度最快，但精度最低。
2、视区(Viewport)
设备坐标系中的一个矩形区域，在图形设备上用来输出图
形的最大区域称之为屏幕域，它是有限的整数域，任何小于
或等于屏幕域的区域都可定义为视区。视区由用户在屏幕
域中用设备坐标定义，一般也由左下角点和右上角
点坐标来表示，同样视区也可以是多层的。而
且，在同一屏幕还可以定义多个视区。
6
视区 窗口
视区
13
3、如果视区的纵横比与窗口的纵横比不一致时，经 变换后的图形在视区中输出时会产生失真现象，因此在定 义窗口和视区时，要保证它们的纵横比一致。
窗口
视区
视区

运动学

运动学

忽略物体的形状和大小， 忽略物体的形状和大小，保留物体原有质量的一个理想 的物理点模型。 的物理点模型。
1）运动过程中，物体各部分运动相同 如物体的平动 )； ）运动过程中，物体各部分运动相同(如 ；
2）物体的尺寸相对运动范围很小。 ）物体的尺寸相对运动范围很小。
▲选择合适的参考系
以方便确定物体的运动性质； 以方便确定物体的运动性质； ▲建立恰当的坐标系 以定量地描述物体的运动； 以定量地描述物体的运动； ▲提出较准确的物理模型 以确定所提问题最基本运动律. 以确定所提问题最基本运动律
2
∆θ t A θ
O
参考
弧度/秒 弧度 秒2（rad/s2)
为恒量的圆周运动，称为匀变速圆周运动。 角加速度β为恒量的圆周运动，称为匀变速圆周运动。
dω = β dt
∫ω
∫θ
θ
0
ω
0
dω = ∫ β dt
0
t 0
t
ω = ω0 + βt
1 2 θ = θ0 +ω0t + βt 2 3 2 ω −ω0 = 2(θ −θ0 )
dv aτ = τ dt
dv d s aτ = = 2 dt dt
沿切向方向
2
描述速度大小随时间的变化快慢，即速率对时间的变化率。 描述速度大小随时间的变化快慢，即速率对时间的变化率。
dτ an = v dt
an =
v
2
ρ
沿法线方向。 沿法线方向。若是圆周运动则指向圆心 描述速度方向随时间的变化快慢，即速度方向的变化率。 描述速度方向随时间的变化快慢，即速度方向的变化率。
dv y
2
2
2
dv x d 2 x = 2 ax = dt dt dv y d 2 y 中 a y = = 2 dt dt 2 a = dvz = d z 2 z dt dt

1-2 质点运动学 (角速度 角加速度 相对运动)

1-2 质点运动学 (角速度 角加速度 相对运动)

在自然坐标系中的质点加速度：
a
d
dv d
dt dt
d
n
(v) dv
dt
d
d
n
v d
dt d ds
dv
dt
n
1
vn
v2
n
dt dt ds dt
ds
v
d
5
a
dv
d
(v)
dv
v2
n
dt dt
dt
切向加速度
a
a
反映速度大小变化
法向加速度
an
v2
n
反映速度方向变化
角加速度
lim d d 2
t0 t dt dt 2
单位：rad/s2
角加速度等于质点的角速度对时间的一阶导数
考虑矢量性 质点的 角d坐标对时间的二阶导数
加速转动
dt
方向一致
减速转动
方向相反
11
角量之间的关系：
匀速圆周运动 是恒量
d dt
d
t dt
0
0
0 t
匀角变速圆周运动
§1-3 自然坐标系 圆周运动
一、自然坐标系
物体的运动状态的物理量：位矢、位移、速度和加速 度。通常建立直角坐标系进行描述。
但直角坐标系统并非总是很方便。例如：汽车在公路 上行使；运动员沿操场跑道跑步；物体沿圆周运动。
通常做法是：是选取一个起点，然后用路程、速度和 加速度描述其运动。
当质点做曲线运动，且运动的轨道已知时，选取一 个起点，然后用路程、速度和加速度描述其运动。
质点作变速直线运动 质点作匀速圆周运动 质点作任意圆周运动
13

自然坐标系

自然坐标系

B
（1）角位置
质点所在位置的矢径与x轴 的夹角θ。
A
R
O
X
（2）角位移
t时刻：
A点，角位置为 t
t t时刻：B点，角位置为 t t
在t时间内，矢径转过角度 ，称为质点
对O点的角位移。
t t t
大小：dθ 方向规定： 逆时针方向 dθ＞0；
顺时针方向 dθ＜0。
单位：弧度rad
（3）角速度
a
dv dt
an
dv n dt
a 由于速度大小变化产生的加速度；
an 由于速度方向变化产生的加速度。
切向加速度、法向加速度/二、2 r
r 为运动轨迹的曲率半径。
大小
a
a 2
a
2 n
dv
2
v 2
2
dt r
对于平面曲线运动 a dv dv dt dt
vn 为速度增量在法线方向的分量； 0 切线方向的单位矢量；
n0 法线方向的单位矢量。
切向加速度、法向加速度/二、a、an
将（1）式两边同除 t 后取极限，
lim v
Δt 0 t
lim
Δ t 0
v t
0
Δlitm0
vn t
n0
有
dv dt
dv dt
0
dv n dt
n0
即 a a0 ann0
其中：
切向加速度、法向加速度/二、a、an
例：一质点作半径为R的圆周运动，其速
率满足 v kRt， k为常数，求：切向加 速度、法向加速度和加速度的大小。
解： 切向加速度
a
dv dt
kR
法向加速度
an

1.3 自然坐标系及运用

1.3 自然坐标系及运用
1.3 自然坐标系及运用 s (t )
1、自然坐标系 (natural coordinates)
利用 t 时刻质点所在处与原点之间轨迹曲线的
长度s(t) 就可以确定质点的位置，s(t) 称为弧坐
标。弧坐标下的质点运动方程：
s s(t)
质点的速率，为弧坐标对时间的一阶变化率
v ds dt
将两个相互垂直的切向和法向所组成的平面
24tR
a an
an R 2 144t 4R
a
a an
24t 144t 4
3 3
2 4t3 2
2
t3 1/2 3 3.15rad
3
0 t t 0 5s
例2：质点沿半径R=0.1m作圆周运动，其角坐标与
时间的关系为 2 4t 3 （SI），当切向加速度的
大小恰为总加速度的一半时，则
。
解：切向加速度大小为总加速度的一半，则
30 a / an tan 30
v R R d 12t 2R
dt
a
R
d 2
R dt 2
an
v
dˆ
dtv2nˆFra bibliotek aa
an
dv ˆ
dt
v2
nˆ
大小：a
a2 an2
( dv )2 (v2 )2
dt
当质点做直线运动时 ，因此法向加速度为零；
当质点做圆周运动时， 为圆周运动的半径 R ；
如果 v 为常数，则切向加速度为零，合加速度方
向指向圆心，称为向心加速度；
3 圆周运动的角量描述
0t
0
0t
1 2
t2
2
2 0
2
(
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
加速度
速度、
2、题设加速度关于时间（坐标）的函数
积分
速度、
运动学方程。需注意积分常量和积分上下限。
2015/3/16
DUT 常葆荣
6

例题
一质点运动轨迹为抛物线
x t 2 y t 4 2t 2
z0
求：x = - 4 m 时（t >0) 的位移、速度、速率、加速度。
2 4 2 解 r t x t i y t j z t k t i t 2t
10
圆周运动 速度
v R j
2 v an R 2 R
沿切线方向
法向加速度
沿半径方向指向圆心
切向加速度
dv a R dt
沿切线方向
2015/3/16
DUT 常葆荣
11
三、自然坐标系
速度：
r r s v lim lim ( ) t 0 t t 0 s t r s r ds ( lim )( lim ) ( lim ) t 0 s t 0 t t 0 s d t

j
r 4i 8 j m
x = -4 t= 2
dr v 2ti 4t 3 4t j d t 1 1 2 2 v 4i 24 j ms v 4 24 4 37 ms
a 2i 12t 4 j
2
a 2 i 4 4 j m s 2
所以
的方向 τ / / n 法线方向指向圆心 d( R ) ds v dτ d n n n n dτ d n Rdt Rdt R dt dt
dv v a n dt R
2



圆周运动 的半径
13
2015/3/16
DUT 常葆荣
dv v a n dt R
v k (l x )
dx 质点沿x方向运动 v k (l x ) dt
O
P
A
x
dx kdt (l x )

x 0
dx (l x )

t 0
kdt
x l e kt
a
DUT 常葆荣
v
2015/3/16
dx ke kt dt
dv k 2 e kt dt
2015/3/16
DUT 常葆荣
20
ds (2) v dt
ds vd t
s

t 0
a τ td t
1 2 s aτ t 2
此即用自然坐标法表示的质点的运动学方程
第2秒内通过的路程
1 s 3 ( 2 2 12 ) 4 .5 m 2
2015/3/16
DUT 常葆荣
在自然坐标系中，只要知道质点的运动学方程s=f(t), 就可 以求出质点在任意时刻速度的大小和方向。
2015/3/16
DUT 常葆荣 12
加速度——对于圆周运动 由定义
dv d ( v ) a dt d t dv a v dt dt d ？
n

当t0， 的大小

v
v
加速度 a 的大小
a 2 a n 2
14
一般的曲线运动
其中 为曲率半径，n的方向指向曲率圆中心
引入曲率圆后，整条曲线就可看成是由许多不同曲率半 径的圆弧所构成 P v aτ A •
d dv dτ dv v2 a (v τ ) τv τ n dt dt dt dt
2015/3/16
dt
DUT 常葆荣
8
例题
一质点沿X轴运动，采用SI单位制，其加速度和位置 在数值上满足a=2+6x。已知在x=0处，速度v=10，求 质点的速度与位置的关系。
解：根据加速度的定义
dv d v d x d x d v dv a v dt dt dx dt dx dx
dv v 2 6x dx
an

a
an

a
v2 an R
变化
a
a
2 2 n
a a a
变化
DUT 常葆荣
a
2015/3/16
an tg a
变化
18
均匀=不变
例题 一汽车在半径 R=200 m 的圆弧形公路上行驶，其运动 学方程为s =20t 0.2 t 2 (SI) . 求 汽车在 t = 1 s 时的速度和加速度大小。
v d v ( 2
6 x )d x
1 2 v 2x 3x2 c 2
根据初始条件，x=0时，v=10.确定积分常数：c=50
1 2 v 2 x 3 x 2 50 2
2015/3/16
v 4 x 6 x2 100
DUT 常葆荣 9
例题 如图，质点沿x轴正方向向A点运动，已知OA=l,设 t=0时，质点位于坐标原点，质点在任意时刻的速率 正比于它所在的位置到A点的距离，比例常量为k， 试求：x,v,a随时间变化的规律。 解：设任意时刻质点位于P点，根据题意
a R 2i R j
d2r 0 2 dt
dr vr 0 dt
2015/3/16
DUT 常葆荣
2
加速度
a R i R j
2
j
O
i

O/
2 v 法向加速度—— 沿半径方向指向圆心 an R 2 R
dv a R dt
只改变速 度的方向
切向加速度——沿切线方向 只改变速 度的大小 质点做圆周运动时线量（速度、 加速度）和角量（角速度、角 加速度）之间的关系


B
an

2 2


a
a aτ a n
2015/3/16
an , tan θ aτ
DUT 常葆荣
15
线量
R
关
系
角量
角位 移 角速 度 角加 速度
o

S 线量S
S=R
d dS R 速度v v R dt dt
圆 周 运 动
切向加 a 速度 法向加 速度
d dv R R dt dt 2 v 2 an R R
2 τ 2 n
dv aτ 0 .4 dt

2
( 20 0 .4 1) a (1) 0 .4 200
2
2015/3/16
DUT 常葆荣
2
2 1 . 44 m/s
19
2
例题 质点沿半径R=3m的圆周运动，已知切向加速度 a=3m/s2, t=0时质点位于O1点，其速度为vO1=0. 试求（1）t=1s时质点速度和加速度的大小（2） 第2秒内质点所通过的路程。 R 解： t=0时质点位于O1点，就以 O1点作为自然坐 标的原点，以质点运动的方向为自然坐标的 正方向。设t时刻质点速度大小为v，自然坐 标为s. v t d v (1) a dv a dt dv a dt
v
dx 2 dy 2 ( ) ( ) dt dt
a
d2x 2 d2 y 2 ( 2) ( 2 ) dt dt

先求矢量的各分量对时间的导数，再求速度和加速度 的模。 正确区别矢量导数的模与矢量模的导数的不同。
2015/3/16
DUT 常葆荣 5
运动学的两类问题
求导
1、题设+坐标系+初始条件运动学方程
21
例题 在离水面高度为h的岸边，有人用v0 的速度收绳拉船靠 岸，求船被拉到离岸边x处的速率。 v0 解：设船速为 。在∆t时间内，船发生的位移为 r 绳缩短的距离为 r r h r dr dr
1
曲线运动的特例——圆周运动
圆周运动：指质点的轨迹在平面极坐标内的投影是一个半 径为R的圆，并且圆心在极点上。
速度
dr v i r j dt dr dR 0 dt dt
v R j
速度只有 沿切线方 向的分量
加速度
d2r a ( 2 r 2 )i ( r 2vr ) j dt
第一项： 切向加速度
2
dv a dt
v n ann R
加速 减速
DUT 常葆荣
dv 大小：a dt
方向：

意义： 反映速度大小变化的快慢
2
第二项： 法向加速度
v2 大小： an R
方向：
n
意义： 反映速度方向变化的快慢
a a a n n
2015/3/16
1、基本概念： 位置矢量 r ：坐标原点质点
dv d r 速度： v d r 加速度： a 2 dt dt dt 2、速度和加速度在不同坐标系中的分量表示
位移 r ：位置矢量的增量
2
直角坐标系
dr 速度 v i r j 平面极坐标系 dt d2r 2 法向加速度 a r 2vr 切向加速度 ar 2 r dt
DUT 常葆荣 3
2 v 2 an R R dv a R dt
2015/3/16
v R
圆周运动 速度
v R j
2 v an R 2 R
沿切线方向
法向加速度
沿半径方向指向圆心
切向加速度
dv a R dt
沿切线方向
2015/3/16
DUT 常葆荣
DUT 常葆荣
2015/3/16
16
讨论
分析行星通过M、N点时速率分别是增大
还是减小？

相关主题