当前位置：文档之家 › 1.3 自然坐标系及运用

1.3 自然坐标系及运用

  • 格式：ppt
  • 大小：608.50 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

坐标系的认识与运用

坐标系的认识与运用

坐标系的认识与运用一、引言在数学和物理学中，坐标系是一种重要的概念，它用于描述和定位空间中的点或物体。

了解和掌握坐标系的基本知识对于解决各种问题是至关重要的。

本文将介绍坐标系的认识与运用。

二、二维坐标系二维坐标系是最基本且常见的坐标系形式。

它由两条互相垂直的数轴组成，分别称为x轴和y轴。

x轴和y轴的交点被称为原点，通常表示为O。

在二维坐标系中，每个点可以用一个有序数对(x, y)来表示，其中x表示点在x轴上的位置，y表示点在y轴上的位置。

三、三维坐标系三维坐标系是在二维坐标系的基础上引入了第三个轴，通常称为z 轴。

在三维坐标系中，每个点可以用一个有序数对(x, y, z)来表示，其中x、y和z分别表示点在x轴、y轴和z轴上的位置。

四、直角坐标系直角坐标系是指坐标轴两两垂直的坐标系。

二维直角坐标系由x轴和y轴组成，而三维直角坐标系则由x轴、y轴和z轴组成。

直角坐标系在几何学、物理学和工程学等领域中广泛应用，可以用于描述和解决各种空间问题。

五、极坐标系极坐标系是一种用极径和极角来表示点的坐标系。

在极坐标系中，每个点用一个有序数对(r, θ)来表示，其中r表示点到原点的距离，θ表示点与x轴之间的夹角。

极坐标系常用于描述圆形、旋转和周期性变化等问题。

六、坐标系的应用坐标系在各种领域中都有广泛的应用。

在数学中，坐标系可以用于解决代数和几何问题，如求解方程、计算距离和求解图形的面积等。

在物理学中，坐标系可以用于描述物体的位置、运动和力的作用方向等。

在工程学中，坐标系可以用于设计和建模，如绘制平面图和三维模型等。

七、小结通过本文的讲解，我们了解了坐标系的基本概念和应用。

无论是二维坐标系还是三维坐标系，无论是直角坐标系还是极坐标系，掌握坐标系的知识和技巧对于解决各种问题都具有重要意义。

希望读者通过学习和实践，能够更好地认识和运用坐标系，提高自己的数学和物理素养。

自然坐标圆周运动相对运动

自然坐标圆周运动相对运动

《关于两门新科学的对话和数学证明对话集》 一书，总结了他的科学思想以及在物理学和天文学 方面的研究成果。
伽利略所取得的巨大成就，开创了近代物理学 的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
（1）位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略（Galileo Galilei，1564—1642）
伽利略杰出的意大利物理学家和 天文学家，实验物理学的先驱者。
他提出著名的相对性原理、惯性 原理、抛体的运动定律、摆振动的等 时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结：自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变 化的快慢
反映速度方向变 化的快慢程度
dv a dt
an
v2
aa
a 2 an 2
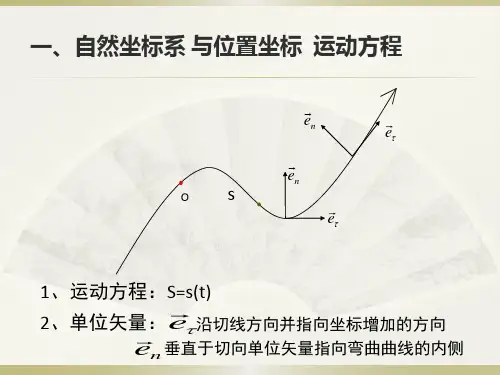
自然坐标系

自然坐标系

2 ω 2 − ω0 = 2 β (θ − θ 0 )
1 2 βt 2
****************************************************** 匀速圆周运动 匀速直线运动 θ = θ 0 + ωt x = x0 + Vt 匀变速圆周运动 匀加速直线运动 ω = ω 0 + βt V = V0 + at 1 1 θ − θ 0 = ω 0t + βt 2 x − x0 = V0 t + at 2 2 2 2 2 2 2 ω − ω 0 = 2 β (θ − θ 0 ) V − V0 = 2 a ( x − x 0 ) ******************************************************
4
V2
V2 ⇒ρ= ：计算曲率半径 （4） a n = ρ an 例： R =800m 的圆形轨道，汽车，静止开始，
速率均匀增加， t =3（分） ， V =20m/s r ， a ， at ， a n 求： t =2（分） 解：设 V = kt ，t=3（分）=180s， V =20m/s
k =20/180=1/9， V = t /9 dV at = = 1 / 9 = 0.111(m / s 2 ) dt t =2（分）=120s， V =120/9(m/s) V2 = 0.222m / s 2 an = R
at
α
an R
O
r a
2 a = at2 + a n = 0.248m / s 2 ， tgα = a n / at =2， α = 63.4 o
第5节
P
相对运动
S ′ 相对于 S 作平动运动 r r r r = r ′ + r0 r r r ∆r = ∆r ′ + ∆r0 r r r dr dr ′ dr0 = + dt dt dt
自然坐标系

自然坐标系


2. a C , an 0
3. a 0 , an C 4. a 0 , an 0
匀变速直线运动；
匀速率圆周运动； 变速曲线运动；
切向加速度、法向加速度/二、a、an
三、圆周运动的角量描述
（1）角位置
质点所在位置的矢径与x轴 的夹角θ。


Y
B
R
A
O

X
（2）角位移
A点，角位置为 t t t时刻：B点，角位置为 t t 在t时间内，矢径转过角度 ，称为质点 对O点的角位移。 t时刻：

t t t
大小：dθ



方向规定： 逆时针方向
顺自然坐标系 切向加速度 法向加速度
一、自然坐标系
自然坐标系
•问题的提出： 在直角坐标系中，加速度公式无法看 出哪一部分是由速度大小变化产生的加速 度，哪一部分是由速度方向变化产生的加 速度，所以引入自然坐标系来描写。 1.自然坐标系 自然坐标系是建立在物体运动的轨 迹上的，有两个坐标轴，切向坐标和法 向坐标。
2
2
r 为运动轨迹的曲率半径。
大小
a a a
2
2 n
dv v dt r
dv dv a dt dt
2
2
对于平面曲线运动
切向加速度、法向加速度/二、a、an
例：一质点作半径为R的圆周运动，其速 率满足 v kRt ， k为常数，求：切向 加速度、法向加速度和加速度的大小。
（3）角速度


d lim t 0 t dt
d 大小： dt

方向：如图
自然坐标系

自然坐标系

系下的加速度
1. 匀速圆周运动， 法向加速度
v vB
vA
v vB
vA
Δv vB vA ,
AB R
lim lim a
t 0
t
t 0
AB .
t R
en
v2 R
en
法向加速度
a
an
v2 R
vB
B vA
R
O
A
大小，方向，作用
2. 一般圆周运动的
切向加速度和法向加速度
ds dt
e
3、自然坐标系下的加速度：a
anen
a e
v2 R
en
dv dt
e
a a n 为法向加速度 为切向加速度
vA
a
d
dt
切向加速度的方向为切线方向 它反映了速度大小的变化, 作用是改变质点的速度大小.
an a
a
a
an2 a2
2
R
2
d
dt
2
a
tg a
an
arctg a ,
an
a an2 a2
an
例题：汽车在半径为200m的圆弧形公路上刹车，刹
车开始阶段的运动方程为 s 20t 0.2t3（单位：m,s）
tg an
a
12233'
总结解题策略：
（1）分析问题特点，建立恰当的坐标系 （2）由运动方程求解速度随时间变化的表达式 （3）分别计算出切向加速度与法向加速度，再 求解合加速度的大小和方向
小结本节内容：
1、自然坐标系下的运动方程及其单位矢量：
S=s(t) en e
2、自然坐标系下的速度：
v
分析方法
自然坐标系

自然坐标系

自然坐标系
自然坐标系是指一个基于自然规律和观测事件的坐标系。

在物理学、地理学、
生物学等领域中，自然坐标系被广泛应用于描述和研究自然现象。

自然坐标系的建立通常以某个客观参照物或事件为基准点，以此构建具有一定方向和单位的坐标轴。

在物理学中，自然坐标系常用于描述空间位置、运动和力等物理量。

其中，笛
卡尔坐标系是最常见的一种自然坐标系，由三个垂直的坐标轴构成，分别代表空间中的长度、宽度和高度。

物体在笛卡尔坐标系中的位置可以通过三个坐标值来确定，这种描述方法简单直观。

在地理学中，地球表面的经纬度坐标就是一种自然坐标系。

经线和纬线交叉形
成网格状结构，用于描述地球表面上的位置。

经纬度坐标在导航、地图绘制等方面有着重要的应用，能够准确描述地球上任意点的位置。

生态学中也常常使用自然坐标系来描述生物群落的分布和生态系统的结构。

例如，树种分布图就是利用自然坐标系进行绘制的，通过对树木种类和数量在空间中的分布进行记录和统计，可以帮助研究者了解生态环境的特点和动态变化。

总的来说，自然坐标系是描述和研究自然现象不可或缺的工具之一。

通过建立
合适的坐标系，可以更好地理解和解释自然规律，促进科学研究和技术发展的进步。

对于不同领域的研究者来说，熟练掌握各种自然坐标系的原理和应用方法非常重要，能够帮助他们更准确地进行科学分析和实验推断。

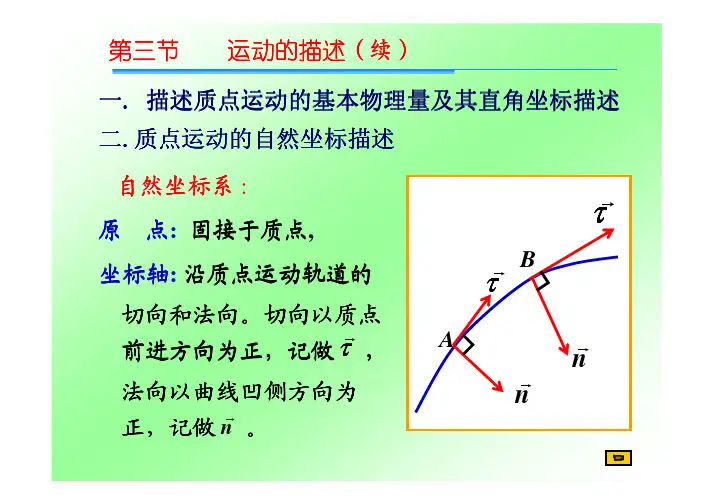
自然坐标极坐标

自然坐标极坐标


dt
dt 2
注意：角加速度不是矢量 （参看《教与学参考》Ｐ71）
5.角量与线量的关系 s = Rθ ∆s = R∆θ
P′( t + ∆t )
∆s
R ∆θ
Oθ
P( t )
s
O' 参考
方向
v = ds = R dθ = Rω
dt
dt
aτ
=
dv dt
=
R dω
dt
=
Rβ
an
=
v2
ρ
=
( Rω
R
)2
=
Rω 2
A
B
第一项
r
∆ vτ
lim
∆t→ 0
∆t
=
lim
∆t→ 0
∆v ∆t
τr
=
d v τv
dt
v
v
∆v
v
A
v ∆s
v A
B
A
v
r
v B
rD r
vA ∆vn
∆v
∆v r C
∆ vτ
∆θ
r vB
E
B
第二项
r
lim
∆t→ 0
∆vn ∆t
=
v∆θ
lim
∆t→ 0
∆t
r n
=
vdθ
dt
r n
y
∆s ∆θ
A
x
o
=
练习
教材第44页例6
某发动机工作时，主轴边缘一点作圆周运动方程为
θ = t 3 + 4 t + 3 ( SI )
（1）t =2s 时，该点的角速度和角加速度为多大？
自然坐标系中的描述及相对运动

自然坐标系中的描述及相对运动


(2) vx v0 , v y gt
o v0
x
v
vx2
v
2 y
v02 g 2t 2
tan1( gt )
v0
y
an
a
g
切向加速度
at
dv dt
g2t v02 g2t 2
与速度同向
总加速度总是竖直向下的重力加速度 g
法向
an
g2 at2
v0 g 与切向加速度垂直 v02 g2t 2
A v1
n B
C
v2
法向加速度大小等于速率平方除以曲率半径， 方向沿轨道的法线指向。
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
a
a
an
dv dt
v2
n
a
an
a
a a a 2 an 2
dv dt
2
v2
2
tg a
an
加速度总是指向曲线的凹侧，因为正 是加速度的法向分量改变了质点的运动方向。
2-2 圆周运动 角量
1、圆周运动中的切向加速度和法向加速度
曲率半径是恒量 a dv v2 n
dt R
匀速圆周运动v c a v2 n 向心加速度
R
2、圆周运动的角量描述
t A
角位置
t t B 角位移
v2 B v1
R s A
沿逆时针转动，角位移取正值
O
X
沿顺时针转动，角位移取负值
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
例2：手球运动员以初速度v0与水平方向成α0 角抛出一球，如图所示。当球到达M点处，与水 平线夹角为θ，求(1)球在M点速度的大小；(2)球 在M点处的切向加速度和法向加速度大小；(3)M 点处的曲率半径。
坐标系的认识和使用

坐标系的认识和使用


坐标系的建立
坐标系的定义：用于描述物体位置和方向的数学工具 坐标系的分类：直角坐标系、极坐标系、柱坐标系等 坐标系的建立方法：选择原点、确定坐标轴、确定单位长度 坐标系的应用：工程设计、科学研究、地图绘制等领域
坐标系的表示方法
直角坐标系
直角坐标系的定义：由两个互相垂直的数轴组成的坐标系 直角坐标系的表示方法：用x、y、z表示坐标值，其中x、y表示平面坐标，z表示空间坐标 直角坐标系的应用：在数学、物理、工程等领域广泛应用 直角坐标系的特点：直观、简单、易于理解和使用
转换应用：在实 际应用中，需要 根据具体需求选 择合适的坐标系 和转换方法，并 注意转换精度对 结果的影响
THANK YOU
汇报人：XXX
球坐标系：由r、 θ、φ三个坐标轴 组成，其中r表示 距离原点的距离， θ表示与x轴的夹 角，φ表示与z轴 的夹角。
变换关系：直角 坐标系中的x、y、 z坐标可以通过球 坐标系中的r、θ、 φ坐标进行转换， 反之亦然。
变换公式： x=r*sin(θ)*cos (φ)， y=r*sin(θ)*sin (φ)， z=r*cos(θ)。
柱坐标系：x轴和y轴相互垂直，z轴 垂直于xy平面
球坐标系：以原点为中心，半径为r， 角度为θ，φ
空间直角坐标系：x轴、y轴、z轴相 互垂直，构成一个立方体
空间极坐标系：以原点为中心，半径 为r，角度为θ，φ，构成一个球体
单位长度和单位选择
单位长度：选择合 适的单位长度，如 厘米、毫米等
单位选择：根据实 际需要选择合适的 单位，如长度、角 度、时间等
坐标系的注意事项
坐标系的原点选择
原点是坐标系的核心，决定了坐标系的位置和方向 原点的选择应根据实际需要和方便计算来确定 原点的选择应避免在坐标轴上，以免引起混淆 原点的选择应尽量在坐标轴的交点处，以便于计算和表示
《自然坐标系》课件

《自然坐标系》课件


自然坐标系的定义
基本概念
• 不同于常规的笛卡尔坐标系、极坐标 系、球坐标系
• 能够更准确地表达物体的真实形状、 大小和位置
特点
• 包含坐标与方位信息 • 内站洼凸性自动转化 • 合理的分带分区结构 • 与国际通用地图厂商软件兼容
自然坐标系的计算方法
点坐标的计算方法 距离的计算方法
根据已知坐标和对应的偏角和距离，可得 出所求点的坐标
自然坐标系
本PPT课件将介绍自然坐标系的基本概念、应用场景及计算方法，以及它在地 图制作和工程设计中的具体应用。希望这份课件能为您带来全新的体验。
相关概念
直角坐标系
由x,y构成的平面直角坐标系
极坐标系
以某点为原点，以该点到直线的距离和该点与极轴正方向的夹角表示平面上其它点的坐标。
球坐标系
将空间点的位置用径向距离r、极角θ、方位角φ这三个参数来表示的坐标系。
国际上常用的大比例尺地图所采用的坐标系统 是自然坐标系。
工程设计
在公路、铁路、港口等大型工程和建筑物的设 计建造中，自然坐标系被广泛用于数据管理和 信息加工。
总结
1 优缺点
2 发展前景
自然坐标系能够更准确地表达物体的真 实形状、大小和位置，但是其计算方法 相对较为繁琐。
在大数据处理和智能交通等领域的应用 逐渐增多，自然坐标系的应用将更加广 泛。
根据正反算公式和高斯投影的方式，通过 计算两点之间的投影距离，得出两点间的 实际距离
自然坐标系的转换
1
自然坐标系和直角坐标系之间的转换
通过正反算公式将自然坐标系的坐标转换为直角坐标系的坐标，间的转换
按一定的方式将自然坐标系转换为极坐标系。
自然坐标系的应用
地图制作
自然坐标系

自然坐标系


B
r(t t)
(2)位移的大小一般不等于路程。 o
x
即 Δ r Δ s
z
当Δt 很小时近似相等，即 r s
当Δt → 0 时
lim r lim s 即 dr ds
t0
t0
1.1.4 速度（描述物体运动快慢及运动方向的物理量）
1.平均速度 t r
总结：确定运动学方程的步骤：
（1）建立（参考系）坐标系 （2）明确起始条件 （3）找出质点坐标随时间变化的函数关系。
1.1.3 位移与路程 1. 位移(描述质点位置变化的物理量)
r r(t t) r(t)
y
B(xB, yB, zB)
A(xA, yA, zA )
r(t)
r r(t t)
a

dv dt

d 2 r dt 2
只要知道运动方程，就可以确定质点在任意时刻的位置、 速度和加速度。
例 如图所示，以恒定
v
xvx (l0 v t)v
速率v 收绳，绳跨 一定滑轮拉湖面上
l0
v
2 x

xax
v2
的船，已知绳初始
h
l(t)
长度 l 0，岸高 h
求 t 时刻船的速度


lim v v //
t 0
t
lim
t 0
v t


lim
t 0
v // t

an
a
讨结论论:：速度r大小r(无t)变化，速v度方d向r 无变化a时的d情v 况 .d2
dt
dt dt
r
2
直角坐标系：
r xi yj zk

1.3坐标系的运用


s ∆
θ
x
υ = rω
dθ
O
ds
r
x
角速度矢量
方向： 方向：角速度矢量 ω 的方向垂直于质点运动 的平面，其指向由右手螺旋定则确定。 右手螺旋定则确定 的平面，其指向由右手螺旋定则确定。 可以得出， r 可以得出，质点的线 r ω 速度 等于角速度 υ r等于角速度 与质 r 的矢量积： 矢量积： 点位矢
ω
r
ω
r
r
r
r υ
r
ω
r
r r υ =ω×r
d ω d 2θ 角加速度： 角加速度： β = = 2 dt dt
r
P
3、 角加速度 (Angular Acceleration ) 、
圆周运动的角量与线量的关系： 圆周运动的角量与线量的关系： 的关系
ds r dθ υ= = = rω dt dt dυ dω aτ = =r = rβ dt dt
τ ∆ˆ
ˆ ˆ dτ = τ dθ= dθ
ˆ ˆ dτ // n, ˆ ˆ dτ = dθ n
法向加速度： 法向加速度：
ˆ r dτ dθ ˆ an =υ =υ n dt dt 2 υ ˆ dθ ds ˆ n =υ n= ρ ds dt
P L
r υ(t)
•
Q
∆θ
•
O•
ρ
r υ(t +∆t)
2 r dυ υ 总加速度： 总加速度： a = aττ + ann = ˆ ˆ ˆ n τˆ + ρ dt
ds = v0 −bt 解：1） v = ） dt dv = −b 2） at = ） dt 2 2 v (v0 − bt ) an = = R R

自然坐标系


B
（1）角位置
质点所在位置的矢径与x轴 的夹角θ。
A
R
O
X
（2）角位移
t时刻：
A点，角位置为 t
t t时刻：B点，角位置为 t t
在t时间内，矢径转过角度 ，称为质点
对O点的角位移。
t t t
大小：dθ 方向规定： 逆时针方向 dθ＞0；
顺时针方向 dθ＜0。
单位：弧度rad
（3）角速度
a
dv dt
an
dv n dt
a 由于速度大小变化产生的加速度；
an 由于速度方向变化产生的加速度。
切向加速度、法向加速度/二、2 r
r 为运动轨迹的曲率半径。
大小
a
a 2
a
2 n
dv
2
v 2
2
dt r
对于平面曲线运动 a dv dv dt dt
vn 为速度增量在法线方向的分量； 0 切线方向的单位矢量；
n0 法线方向的单位矢量。
切向加速度、法向加速度/二、a、an
将（1）式两边同除 t 后取极限，
lim v
Δt 0 t
lim
Δ t 0
v t
0
Δlitm0
vn t
n0
有
dv dt
dv dt
0
dv n dt
n0
即 a a0 ann0
其中：
切向加速度、法向加速度/二、a、an
例：一质点作半径为R的圆周运动，其速
率满足 v kRt， k为常数，求：切向加 速度、法向加速度和加速度的大小。
解： 切向加速度
a
dv dt
kR
法向加速度
an

1.3 自然坐标系及运用

1.3 自然坐标系及运用 s (t )
1、自然坐标系 (natural coordinates)
利用 t 时刻质点所在处与原点之间轨迹曲线的
长度s(t) 就可以确定质点的位置，s(t) 称为弧坐
标。弧坐标下的质点运动方程：
s s(t)
质点的速率，为弧坐标对时间的一阶变化率
v ds dt
将两个相互垂直的切向和法向所组成的平面
24tR
a an
an R 2 144t 4R
a
a an
24t 144t 4
3 3
2 4t3 2
2
t3 1/2 3 3.15rad
3
0 t t 0 5s
例2：质点沿半径R=0.1m作圆周运动，其角坐标与
时间的关系为 2 4t 3 （SI），当切向加速度的
大小恰为总加速度的一半时，则
。
解：切向加速度大小为总加速度的一半，则
30 a / an tan 30
v R R d 12t 2R
dt
a
R
d 2
R dt 2
an
v
dˆ
dtv2nˆFra bibliotek aa
an
dv ˆ
dt
v2
nˆ
大小：a
a2 an2
( dv )2 (v2 )2
dt
当质点做直线运动时 ，因此法向加速度为零；
当质点做圆周运动时， 为圆周运动的半径 R ；
如果 v 为常数，则切向加速度为零，合加速度方
向指向圆心，称为向心加速度；
3 圆周运动的角量描述
0t
0
0t
1 2
t2
2
2 0
2
(

自然坐标系中的速度、加速度


速度的矢量表示
总结词
速度的矢量表示包括大小和方向两个方 面，通常用箭头表示方向，用绝对值表 示大小。
VS
详细描述
矢量表示法是速度最常用的表示方法，它 能够完整地描述速度的大小和方向。在自 然坐标系中，速度的大小由箭头的长度表 示，箭头的指向代表速度的方向。
速度的标量表示
总结词
速度的标量表示只考虑速度的大小，忽略方向，通常用绝对值表示。
特点
自然坐标系与质点运动的具体轨迹相 关，可以直观地描述速度和加速度的 方向和大小。
自然坐标系的应用
描述曲线运动
自然坐标系常用于描述质点在曲线上 的运动，如行星绕太阳的椭圆轨道运 动。
分析动力学
在分析力学中，自然坐标系用于描述 质点的速度和加速度，进而研究其动 力学行为。
自然坐标系与直角坐标系的区别与联系
02
03
健康管理
在健康管理中，个人的速度和加速度 可以用来监测身体的运动状态，从而 进行科学的健身计划和健康管理。
THANKS FOR WATCHING
感谢您的观看
定义法
根据加速度的定义式计算，即加速度等于速度的变化量除以时间的变化量。
公式法
根据加速度的公式计算，即加速度等于速度的导数或切向加速度。
02
速度在自然坐标系中的 表示
速度的定义
总结词
速度是描述物体运动快慢的物理量，定义为物体在单位时间内通过的位移。
详细描述
速度是矢量，具有大小和方向，通常用符号"v"表示。在自然坐标系中，速度的 大小等于物体在单位时间内通过的直线距离，方向则与物体位移的方向相同。
详细描述
匀速直线运动是指物体在直线轨道上以恒定速度进行的运动，其方程为 $s = v_0t$，其中 $s$ 是位移， $v_0$ 是初始速度，$t$ 是时间。

大学物理课件复习资料坐标系的运用


例1：一质点作匀速率圆周运动，半径为 r ，角速度 ：一质点作匀速率圆周运动， 质点的运动学方程。 为 ω 。求：质点的运动学方程。 1）用直角坐标、位矢表示；2）用自然坐标表示。 ）用直角坐标、位矢表示； ）用自然坐标表示。 以圆心O 为原点。 解： 以圆心 为原点。建立直角 坐标系Oxy ，O ′点为初始位置， 点为初始位置， 坐标系 设 t 时刻质点位于 P（x , y）， （ ）， 质点的运动学方程为： 质点的运动学方程为： 1） x = r cosω t , y = r sinω t ） 用位矢表示为： 用位矢表示为：
∆s
θ
x
υ = rω
dθ
O
ds
r
x
角速度矢量
方向： 方向：角速度矢量 ω 的方向垂直于质点运动 的平面，其指向由右手螺旋定则确定。 右手螺旋定则确定 的平面，其指向由右手螺旋定则确定。 可以得出， 可以得出，质点的线 ω 速度 等于角速度 υ 等于角速度 与质 r 的矢量积： 矢量积： 点位矢
ω
r
ω − kθ
2 0
2
例8：已知运动方程 x = ut y = − gt 2 / 2 ： u , g 为常量，求： at , an 为常量， 解： 这显然是平抛运动（依据迭加原理） 这显然是平抛运动（依据迭加原理） 方程在直角坐标系中给出， 方程在直角坐标系中给出，在自然坐标系中求解
θ
a
1）一般曲线运动的法向加速度指向瞬时曲率中心； ）一般曲线运动的法向加速度指向瞬时曲率中心； 2）在曲线运动中，加速度的方向总是指向曲线 ）在曲线运动中， 凹的一侧。 凹的一侧。
讨论
dυ υ ˆ ˆ ˆ a = aττ + ann = n τˆ + dt ρ

自然坐标系的概念

自然坐标系的概念
自然坐标系是用来模拟多体系统的一系列点的笛卡尔坐标或单位向量的三个笛卡尔分量，这些点往往取在运动副或感兴趣的点上，单位向量常取在运动副的轴线或特定方向上。

自然坐标系是沿质点的运动轨迹建立的坐标系，在质点运动轨迹上任取一点作为坐标原点O，两个方向是这样定义的：“切向”（用字母τ表示），沿质点所在点的轨迹切线方向；“法向”（用字母n表示），垂直于在同一点的切向而指向曲线的凹侧。

在自然坐标系中，表示质点的速度非常简单，因为无论质点处在什么位置上速度都只有“切向”分量，而没有“法向”分量。

在该坐标系下，力也是按照这两个方向分解的。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

定义角速度(angular velocity)为
d dt


以及角加速度为
d d 2 dt dt
2

在圆周运动中，角速度、角加速度的方向都 沿转轴，因此一般不用矢量表示，而是写成对转 轴ds d (r ) v r dt dt
若a=恒量，则
o 2ax
1 2 x ot at 2 2 2
o at
若恒量,则
o t 1 2 ot t
o 2
2 2
2
讨论
对于作曲线运动的物体，以下几种说法中哪一种 是正确的： （A）切向加速度必不为零； （B）法向加速度必不为零（拐点处除外）； （C）由于速度沿切线方向，法向分速度必为零， 因此法向加速度必为零； （D）若物体作匀速率运动，其总加速度必为零；
质点的加速度
ˆ dv d dv d ˆ ˆ a (v ) v dt dt dt dt
d dt
沿切向 (ˆ) 的速 dv ( )称 率变化率 dt 切向加速度 a dv a ˆ dt d 2s 2 ˆ dt
其中
是 ˆ 的时间变化率,
ˆ 是切向单位矢量,
当质点做圆周运动时， 为圆周运动的半径 R ； 如果 v 为常数，则切向加速度为零，合加速度方 向指向圆心，称为向心加速度；
3 圆周运动的角量描述
一质点A作圆周运动
角坐标 ，其值随时间变化
r
(t )
角位移 ，
(t t ) (t )
有限大角位移 不是 矢量，而无限小角位 移是矢量，用d 表示
将两个相互垂直的切向和法向所组成的平面 ˆ ˆ 坐标系称为自然坐标系 ( , n) 。
速度矢量在自然坐标系中表述为：
ds ˆ ˆ v v dt
2 自然坐标系下 加速度的表达式
ˆ dv d dv d ˆ ˆ a (v ) v dt dt dt dt
0 t
0 0t 1 t 2 2 2 02 2 ( 0 )
圆周运动(circular motion)与直线运动的比较：
直线运动 坐标 x
圆周运动 角坐标
速度 加速度
dx dt d a dt
角速度 角加速度
d dt d dt
ˆ 沿法向(n)，称法向加速度 an ˆ v2 d ˆ an v n dt
v dv ˆ a a an ˆ n dt
dv 2 v 2 大小：a a a ( ) ( ) dt
2 2 n 2
2
当质点做直线运动时 ，因此法向加速度为零；
1.3 自然坐标系及运用
1、自然坐标系 (natural coordinates)
s(t )
利用 t 时刻质点所在处与原点之间轨迹曲线的 s 长度 s(t ) 就可以确定质点的位置， (t ) 称为弧坐 标。弧坐标下的质点运动方程：
s s (t )
质点的速率，为弧坐标对时间的一阶变化率
ds v dt
其大小恒为1（即单位长度） 故
d dt
是指
切线方向的时间变化率
切向变化率
d dt
分析
t 0, 0,
大小 ˆ ＝ ˆ ˆ 方向 n dˆ d d ( ) ˆ ˆ 则 n n dt dt dt 1 ds v ˆ ˆ n n dt
v2
ˆ2
ˆ n2
o
v1
ˆ1
ˆ n1

2
ˆ

ˆ1
ds 曲率半径 . 其中 d
质点的加速度
ˆ dv d dv d ˆ ˆ a (v ) v dt dt dt dt
沿切向 (ˆ) 的速 dv ( )称 率变化率 dt 切向加速度 a dv a ˆ dt d 2s 2 ˆ dt
dv d (r ) a r dt dt
v 2 an r r
2
匀速率圆周运动和匀变速率圆周运动 ① 匀速率圆周运动：速率 v 和角速度 都为 常量 .
at 0
如
ˆ ˆ a an n r 2n
② 匀变速率圆周运动
t 0 时,
常量 0 , 0
an
2
0 10rad/s
再由 求得
0 t 0 t 5s
例2：质点沿半径R=0.1m作圆周运动，其角坐标与 时间的关系为 2 4t 3 （SI），当切向加速度的 大小恰为总加速度的一半时，则 。
解： 切向加速度大小为总加速度的一半，则 a / an tan 30 30 d 2 v R R 12t R dt 2 a d a R R 2 24tR dt an R 2 144t 4 R a a 24t 3 4 t 3 1/ 2 3 an 144t 3 2 3 3.15rad 2 4t 2 3
（E）若物体的加速度 速率运动 .
a为恒矢量，它一定作匀变
例1： 一飞轮，从静止开始以恒角加速度2 rad s 转动，经过某一段时间后开始计时，在 5s 内飞轮 转过75 rad，问在开始计时以前，飞轮转动了多长时 间？ 1 2 解： 匀角加速运动， 0 t t 2 t 5s 代入 2rad/s 75rad 75 50 25