自然坐标系优秀课件

已知： vA 1940km h1 vB 2192km h1
（2）在时间
t
t 3s
内矢径
r
AB 3.5km
所转过的角度
为
A
At
v A
1 2
t2 vA t 1 at t2
r 2r
飞机经过的路程为
r an
o
B
a
at
v B
s
r
v At
1 2
att
2
代入数据得
s 1722m
第11页/共26页
an (t) a 2 at2
[例 (旧考题)] 某质点的运动方程为 r (t) ti t2 j t3 k
23
(采用SI单位制) ，则t=1秒时该质点运动的切向加速
度大小为(单位：米/秒2)
（C ）
(A) 0 (B) 2 (C) 3 (D) 5
第15页/共26页
第二类运动学问题技巧举例——
例 如图示，一实验者 A 在以 10 m/s 的速率沿水 平轨道前进的平板车上控制一台射弹器, 此射弹器以与 车前进方向呈120 度角斜向上射出一弹丸 . 此时站在地 面上的另一实验者 B 看到弹丸铅直向上运动, 求弹丸上 升的高度 . [分析：有相对运动，参考系间联系？]
v' v
解 设地面参考系为 S 系
[分析] 求什么？怎么求? (定义?原理?) 已知什么情形?
A
v A
r an
o
a
B
at
v B
解（1）因飞机作匀变速率
运动所以 at 和 为常量 .
at
dv dt
分离变量有
vB dv
vA
t
0 atdt

r

t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a

an

v2 R


vB

B vA
R

O
A
大小，方向，作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er

ds dt
er


ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动， 法向加速度
v vB
vA

v vB
vA
Δv vB vA ,

AB R
lim lim ar
t 0
则：a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略：
（1）分析问题特点，建立恰当的坐标系 （2）由运动方程求解速度随时间变化的表达式 （3）分别计算出切向加速度与法向加速度，再 求解合加速度的大小和方向
解：根据加速度的定义：
ar
anern
a er

v2 R
ern

dv dt
er
a an2 a 2
v

ds dt
2
R
a

d
dt
1.2t

表示天体在天球上的位置 东度量，自0-24h。
黄道坐标系：黄纬和黄经
• 基圈是黄道
• 原点是春分点，始圈是 无名圈
• 纬度为黄纬，是天体相 对于黄道的方向和角距 离0-90度
表示日明行星在星 空间的位置和运动
• 经度称黄经，是天体所 在黄经圈相对于春分点 所在黄经圈的方向和角 距离，0-360度。以春 分点为起点向东度量。
天顶
天北极
天赤道
地平圈
天底
天南极
• 地平圈：两极为天顶、天底
• 天赤道：两极为天北极、天南 极
• 黄道：两极为黄北极、黄南极
天球视运动—周日运动
• 地外的天空，包括日月星辰均以与地球 自转相反的方向和相同的周期运动，即 天球周日运动。
• 在北半球，天球周日运动绕转中心是天 北极，紧邻天北极较明亮的恒星即为北 极星。
用于时间的度量
• 经度称时角，是天体所在 赤经圈相对于午圈的方向 和角距离，以上点为起点， 沿天赤道向西度量，为的 是使天体的时角与时俱增。
第二赤道坐标系：赤纬和赤经
• 基圈是天赤道，
• 原点是春分点，始圈是 春分圈。
• 纬度是赤纬，与第一赤 道坐标系相同
• 经度为赤经，天体所在 时圈相对于春分圈的方 向与角距离。赤经以春 分点为起点沿天赤道向
• 基圈是地平圈
• 原点通常是南点， 始圈是午圈
• 地平纬度称为高度， 是天体相对于地平 圈的方向和角距离，
• 地平经度为方位， 天体所在地平经圈 相对于午圈的方向 和角距离，以南点 为起点沿地平圈向 西度量。
第一赤道坐标系：赤纬和时角
• 基圈是天赤道
• 原点是上点，始圈是午圈
• 纬度称赤纬，是天体相对 于天赤道的南北方向与角 距离。

(－ )/2 ，当 0, d
当 t 0 时
τ τ (t ) θ θ
τ // n τ θ n
θ θ s 1 dτ τ lim n lim n vn lim t 0 s t ρ dt t 0 t t 0 t
2
a an 2 aτ 2 230.5 m/s2
(2) 设t′时刻，质点的加速度与半径成45 角，则
o
aτ an
4
rω2 rβ
144t ' 24t ' t ' 0.55 s
2 4t ' 2.67 rad
3
2015-2-18 第1章 质点运动学 16
例4 一质点在水平面内以顺时针方向沿半径为2 m 的 圆形轨道运动。此质点的角速度与运动时间的平方成 正比，即ω=kt 2 ，k 为待定常数.已知质点在2 s 末的线 速度为 32 m/s 。求t =0.5 s 时质点的线速度和加速度。
1s t2 3s 之间的路程
。
解 质点运动速度为 速率为
dr d ˆ t2 ˆ ˆ 2t ˆ v (2ti j ) 2i j dt dt
2 2 2 2 2
v v x v y 2 4t 2 1 t
2
路程满足 ds v dt 2 1 t dt
ds dτ 1 v2 v v n n an dt dt ρ ρ
法向加速度： 大小为
2015-2-18
曲率半径
2 ρ 方向为
第1章 质点运动学
n
意义： 反映速度方向变化的快慢
它是与该点切 向垂直并指向 曲线凹侧的法 向单位矢量
4
法向加速度与切向加速度

证明以上两式22naaa???222vdtdv?????????????????????????????????对于平面曲线运动dtdav?dtdv?大小2切向加速度法向加速度二a??an例
第二节 自然坐标系 切向加速度 法向加速度
一、自然坐标系 •问题的提出： 在直角坐标系中，加速度公式无法看 出哪一部分是由速度大小变化产生的加速 度，哪一部分是由速度方向变化产生的加 速度，所以引入自然坐标系来描写。 1.自然坐标系 自然坐标系是建立在物体运动的轨 迹上的，有两个坐标轴，切向坐标和法 向坐标。
2. a C , an 0
3. a 0 , an C 4. a 0 , an 0
匀变速直线运动；
匀速率圆周运动； 变速曲线运动；
§2切向加速度、法向加速度/二、a、an
例
解：
vห้องสมุดไป่ตู้
a

g
an
v
想一想：何处 曲率半径最大？ 何处最小？
dv a kR 解： 切向加速度 dt 2 2 ( kRt) v 2 2 法向加速度 a n k Rt R 2 2 加速度 a a an

kR k Rt
2 2
2 2
§2切向加速度、法向加速度/二、a、an
讨论下列几种运动情况：
1. a 0 , an 0 匀速直线运动；
v v 0 vnn0 （1）
v A n B v vB τ 其中 v 为速度增量在切线方向的分量；
vn
vn 为速度增量在法线方向的分量； 0 切线方向的单位矢量；
n0
vA
vA
法线方向的单位矢量。
§2切向加速度、法向加速度/二、a、an

1.3 自然坐标系及运用 s (t )
1、自然坐标系 (natural coordinates)
利用 t 时刻质点所在处与原点之间轨迹曲线的
长度s(t) 就可以确定质点的位置，s(t) 称为弧坐
标。弧坐标下的质点运动方程：
s s(t)
质点的速率，为弧坐标对时间的一阶变化率
v ds dt
将两个相互垂直的切向和法向所组成的平面
24tR
a an
an R 2 144t 4R
a
a an
24t 144t 4
3 3
2 4t3 2
2
t3 1/2 3 3.15rad
3
0 t t 0 5s
例2：质点沿半径R=0.1m作圆周运动，其角坐标与
时间的关系为 2 4t 3 （SI），当切向加速度的
大小恰为总加速度的一半时，则
。
解：切向加速度大小为总加速度的一半，则
30 a / an tan 30
v R R d 12t 2R
dt
a
R
d 2
R dt 2
an
v
dˆ
dtv2nˆFra bibliotek aa
an
dv ˆ
dt
v2
nˆ
大小：a
a2 an2
( dv )2 (v2 )2
dt
当质点做直线运动时 ，因此法向加速度为零；
当质点做圆周运动时， 为圆周运动的半径 R ；
如果 v 为常数，则切向加速度为零，合加速度方
向指向圆心，称为向心加速度；
3 圆周运动的角量描述
0t
0
0t
1 2
t2
2
2 0
2
(

10
许多图形应用涉及到几何变换，主要包括平移、旋转、缩放。以矩 阵表达式来计算这些变换时，平移是矩阵相加，旋转和缩放则是矩 阵相乘，综合起来可以表示为p' = p *m1+ m2(m1旋转缩放矩阵， m2为平移矩阵， p为原向量 ，p'为变换后的向量)。引入齐次坐标 的目的主要是合并矩阵运算中的乘法和加法，表示为p' = p*M的形 式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点 集从一个坐标系变换到另一个坐标系的有效方法。
6
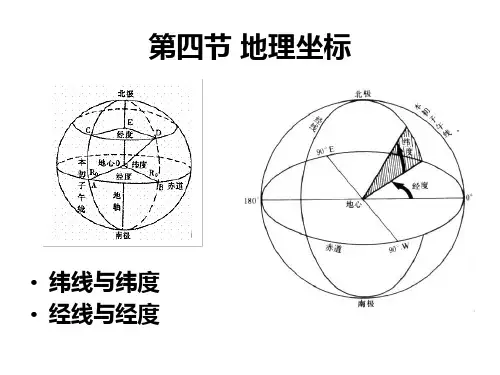
极坐标系
极坐标中会定一点为极点，再将一条通过极点的射线定 为极轴。若给定一角度θ，则可绘出通过极点，和极轴 夹角为θ的唯一射线（角度是以从极轴，依逆时针方向 旋转到射线），若再给定一实数r，可找出上述射线上， 距极点距离为有号整数r的一点[7]。
在极坐标系中，一坐标（r, θ）只会其对应唯一的一 点 ， 但 每 一 点 均 可 对 应 许 多 个 坐 标 。 例 如 坐 标 （ r, θ）、 （r, θ+2π）及（−r, θ+π）都是对应同一 点的不同坐标。而极点的坐标为（0, θ），θ可为任 意值。
当汽车呼啸着从我们身边驶过，在我们的眼中，显然它 的运动就是在标系
所谓齐次坐标就是将一个原本是n维的向量用一个n+1维 向 量 来 表 示 。 例 如 ， 二 维 点 (x,y) 的 齐 次 坐 标 表 示 为 (hx,hy,h)。由此可以看出，一个向量的齐次表示是不 唯一的，齐次坐标的h取不同的值都表示的是同一个点， 比 如 齐 次 坐 标 (8,4,2) 、 (4,2,1) 表 示 的 都 是 二 维 点 (4,2)。
4
笛卡儿坐标系
笛卡儿坐标系也称为直角坐标系，是最常用到的 一种坐标系。在平面上，选定二条互相垂直的线 为坐标轴，任一点距坐标轴的有号距离为另一轴 的坐标，这就是二维的笛卡儿坐标系，一般会选 一条指向右方水平线称为x轴，再选一条指向上方 的垂直线称为y轴

切向加速度、法向加速度 二 切向加速度、法向加速度/二、aτ、an
三、圆周运动的角量描述
（1）角位置 ）
质点所在位置的矢径与x轴 的夹角θ。
∆θ
v
Y
B
R
A X
O
v
θ
（2）角位移 ）
A点，角位置为θ (t ) v t + ∆t时刻：B点，角位置为θ (t + ∆t ) v 在∆t时间内，矢径转过角度∆θ ，称为质点 t时刻：
自然坐标系 切向加速度 法向加速度
一、自然坐标系 自然坐标系 •问题的提出： 问题的提出： 问题的提出 在直角坐标系中， 在直角坐标系中，加速度公式无法看 出哪一部分是由速度大小变化 速度大小变化产生的加速 出哪一部分是由速度大小变化产生的加速 哪一部分是由速度方向变化 速度方向变化产生的加 度，哪一部分是由速度方向变化产生的加 速度，所以引入自然坐标系来描写。 速度，所以引入自然坐标系来描写。 1.自然坐标系 自然坐标系 自然坐标系是建立在物体运动的轨 迹上的，有两个坐标轴，切向坐标和 迹上的，有两个坐标轴，切向坐标和法 向坐标。 向坐标。
n0
法线方向的单位矢量。 法线方向的单位矢量。
切向加速度、法向加速度 二 切向加速度、法向加速度/二、aτ、an
后取极限， 将（1）式两边同除 ∆t 后取极限， ） ∆v lim ∆vτ ∆vn lim = lim τ 0 + Δt→0 n0 Δ →0 ∆t t Δ →0 ∆t t ∆t 有 即
dv dvτ dvn = τ0 + n0 dt dt dt
线量
ds v= dt
v2 an = r
s = rθ
=r
角量 dθ
dt
= rω