2013-01-2自然坐标系下的速度-加速度

自然坐标系的加速度公式推导详解在物理学中，加速度是描述物体速度变化率的物理量。

在自然坐标系中，我们可以通过推导得到加速度的计算公式。

假设一个物体在自然坐标系中运动，我们可以用矢量表示其位置、速度和加速度。

考虑一个时间间隔Δt内，物体的速度从v1变为v2，位移从r1变为r2。

根据定义，平均加速度a平均可以表示为：a平均 = (v2 - v1) / Δt为了得到瞬时加速度a，我们需要让时间间隔Δt趋近于0。

这样，我们可以写出加速度的定义：a = lim(Δt→0) [(v2 - v1) / Δt]接下来，我们将推导加速度的具体计算公式。

首先，我们将速度v 与位移r之间的关系进行分析。

根据定义，速度可以表示为位移对时间的导数：v = dr / dt其中，dr表示位移的微小变化，dt表示时间的微小变化。

我们可以将位移r表示为速度v对时间t的积分：r = ∫v dt现在，我们对上述等式两边进行微分，得到：dr = v dt将上式代入加速度的定义公式，得到：a = lim(Δt→0) [(v2 - v1) / Δt]= lim(Δt→0) [(dr2 / dt - dr1 / dt) / Δt]我们可以对上式进行化简。

首先，将分子展开得到：a = lim(Δt→0) [(∆r / ∆t - ∆r / ∆t)]= lim(Δt→0) [∆r / ∆t - ∆r / ∆t]然后，我们可以将上式中的分式展开：a = lim(Δt→0) [(∆r1 / ∆t - ∆r2 / ∆t)]= lim(Δt→0) [(r1 - r2) / ∆t]我们可以将分式中的∆t约去，得到最终的加速度公式：a = lim(Δt→0) [(r1 - r2) / ∆t]= d(r1 - r2) / dt我们得到了自然坐标系中加速度的计算公式：a = d(r1 - r2) / dt这个公式描述了物体在自然坐标系中的加速度，它表示了速度的变化率。

§2、速度、加速度的分量表达式上一次课，我们为了将运动的一些特征能直接的表示出来，而定义了速度和加速度，22;dt r d dt v d a dt r d v =≡≡ 。

在一般情况下它们往往都是时间t 的函数。

何谓定义呢？定义它本身不是可以用什么方法或者数学手段加以证明得到的，而是根据实际需要常常用到而定义下来的名称和概念。

例如过两点成一条直线……。

由于速度和加速度都是矢量，因此都可以将它们表示成分量的形式。

这次课将准备讨论速度、加速度在各种坐标系中的表达式。

一、 直角坐标系——直角坐标系又称笛卡儿坐标系在直角坐标系中，质点的位置矢径可以写成为：........z k y j x i r ++= （1）根据速度的定义可知dtr d v ≡将（1）代入，则有 1、速度： z y x v k v j v i dt dz k dt dy j dt dx i z k y j x i dt d dt r d v ++=++=++==...........................................)(于是，我们比较上面的等式，就可得到速度在直角坐标系中的分量表达式为：z dtdz v y dt dy v x dt dx v z y x ======;;可见速度沿三直角坐标轴的分量（即分速度）就等于其相应的坐标对时间t 的一阶导数。

速度的大小：222z y x v v v v v ++== 速度的方向就用方向余弦来表示：vv k v v v j v v v i v z y y ===),cos(;),cos(;),cos( 。

同理，我们由加速度的定义不难得到它的分量表达式。

2、加速度根据加速度的定义：zy x z y x a k a j a i dt dv k dt dv j dt dv i dt z d k y d j x d i dt dz k dy j dx i dt d dt v d a ++=++=++=++==2222)(比较这些恒等式可得加速度的直角坐标分量表达式：z dt z d v dv a y dt y d v dt dv a x dtx d v dt dv a z t z y y y x x x ============222222 于是可得加速度的大小为：222z y x a a a a a ++== 加速度的方向用方向余弦表示。

自然坐标系的加速度公式推导详解在物理学中，加速度是描述物体运动状态的重要物理量。

加速度可以通过自然坐标系的公式进行推导和计算。

本文将详细解释自然坐标系的加速度公式的推导过程。

我们需要明确什么是自然坐标系。

自然坐标系是一种用来描述物体运动的参考系，它的基底与物体的运动方向一致。

在自然坐标系中，我们可以使用一组向量来表示物体的位置、速度和加速度。

假设一个物体在自然坐标系中的位置为P，其位置矢量为r。

我们可以将r表示为r = xi + yj + zk，其中i、j、k分别表示坐标轴x、y、z的单位向量。

当物体运动时，其位置会随时间发生变化。

假设物体在t时刻的位置为P(t)，则其位置矢量r(t)也会随时间变化。

我们可以通过求导的方式来描述物体的速度和加速度。

首先我们求解速度。

速度是位置矢量对时间的导数，即v = dr/dt。

由于位置矢量r = xi + yj + zk，我们可以将速度v表示为v = (dx/dt)i + (dy/dt)j + (dz/dt)k。

这就是自然坐标系中的速度公式。

接下来，我们求解加速度。

加速度是速度对时间的导数，即 a = dv/dt。

我们已经知道速度v = (dx/dt)i + (dy/dt)j + (dz/dt)k，因此我们需要对速度进行求导。

对速度的各个分量进行求导，得到加速度的公式：ax = d²x/dt²ay = d²y/dt²az = d²z/dt²这就是自然坐标系中的加速度公式。

根据这个公式，我们可以计算物体在自然坐标系中的加速度。

需要注意的是，自然坐标系中的加速度公式是基于时间的二阶导数计算得到的。

因此，在实际应用中，我们需要通过测量物体的位置随时间的变化来计算加速度。

可以使用传感器或者运动学实验来获取位置和时间的数据，从而计算出加速度。

总结一下，自然坐标系的加速度公式是通过对速度进行求导得到的。

加速度是描述物体运动状态的重要物理量，可以通过测量物体的位置随时间的变化来计算。

自然坐标系
作者：Michaelexe
自然坐标系中的速度和加速度
在质点的平面曲线运动中，当运动轨迹已知时，常用自然坐标系表述质点的位置、路程、速度和加速度。

如图所示，在某质点运动的轨迹线上任取一点O为自然坐标原点，以质点所在位置P点与O点间轨迹的长度s来确定质点的位置，则称s为质点的自然坐标，即
当质点经Δt从P点达Q点时，Δt内质点运动的路程为
设t时刻质点处于P点，在质点上做相互垂直的两个坐标轴，一个轴沿轨道切向指向质点前进方向，其单位矢量用表示；另一轴沿轨道法向指向轨道凹侧，其单位矢量用表示。

由于切向和法向坐标轴随
质点沿轨道的运动自然变换位置和方向，通常称这种坐标系为自然坐标系。

当质点沿平面曲线运动时，其速度矢量的大小（速率）可以写为
考虑其速度方向为轨道的切向，则速度矢量可表示为
下面我们讨论质点的加速度
为质点的切向加速度，它只改变速度的大小，所以
为质点的法向加速度，它只改变速度方向，所以
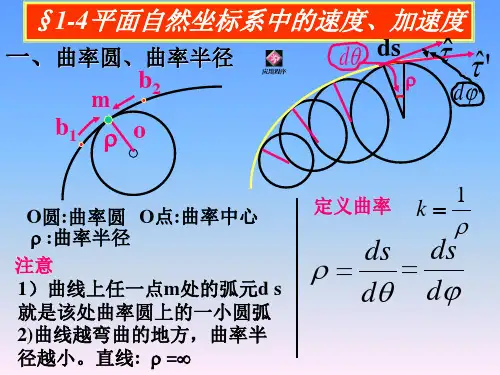
，其中为轨道曲线在该点的曲率半径（因为始终指向轨道内侧，故ρ始终大于0，所以ρ也可以定义为）
所以，
现在来求平面曲线y=f(x)的曲率和曲率半径
曲率的定义：
曲率半径的定义：
下面来求k和ρ的公式所以，。

自然坐标系的加速度公式推导详解在物理学中，加速度是描述物体速度变化率的量。

在自然坐标系中，加速度可以通过公式推导得出。

本文将详细解释自然坐标系下的加速度公式推导过程。

我们需要了解自然坐标系的基本概念。

自然坐标系是一种以物体所在位置为原点的坐标系，它的坐标轴与物体的运动方向相一致。

在自然坐标系中，物体的加速度可以分解为水平加速度和垂直加速度两个分量。

接下来，我们来推导自然坐标系下的加速度公式。

假设物体的水平加速度为a_x，垂直加速度为a_y。

根据牛顿第二定律，物体的合力等于质量乘以加速度。

在自然坐标系中，合力可以分解为水平分力和垂直分力。

水平分力可以用物体质量乘以水平加速度来表示。

垂直分力可以用物体质量乘以垂直加速度来表示。

根据分力的定义，我们可以得到以下两个方程：F_x = m * a_x (1)F_y = m * a_y (2)其中，F_x和F_y分别代表物体的水平分力和垂直分力，m代表物体的质量。

我们可以利用三角函数来表示加速度和分力之间的关系。

根据三角函数的定义，我们可以得到以下两个方程：F_x = F * cosθ (3)F_y = F * sinθ (4)其中，F代表物体的合力，θ代表合力与水平方向的夹角。

将方程(3)和方程(4)代入方程(1)和方程(2)，我们可以得到以下两个方程：m * a_x = F * cosθ (5)m * a_y = F * sinθ (6)接下来，我们可以通过方程(5)和方程(6)来推导自然坐标系下的加速度公式。

我们将方程(6)除以方程(5)，得到以下等式：a_y / a_x = (F * sinθ) / (F * cosθ)化简后可以得到：a_y / a_x = tanθ根据三角函数的定义，我们知道tanθ等于斜率。

因此，我们可以得到以下等式：a_y / a_x = 斜率这意味着自然坐标系下的加速度的垂直分量与水平分量之间的比值等于斜率。

我们可以通过求导来得到自然坐标系下的加速度公式。