当前位置：文档之家 › 塑性理论应力应变关系例题

塑性理论应力应变关系例题

  • 格式：doc
  • 大小：34.50 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

塑性应力应变关系

塑性应力应变关系

2 加载条件
单轴情况
f 0, 且 f 0, 且 f 0, 且
多轴情况
f d ij 0时，加载 ij f d ij 0时，中性变载 ij f d《0时，卸载 ij ij
对理想塑性材料，则为
f f 0, and d ij 0 ij f f 0, and d ij 0 ij
5 塑性应力应变关系的推导
有
0
p ii
（塑性体积应变为零）
令
f f n / σ σ
（屈服面外法向单位向量）
f f f f f : σ σ σ ij ij
n :n 1
f d nij σ
p ij
（流动法则）
作为塑性变形的度量，引进等效塑性变形及其增量
加载或中性变载
卸载
f<0 and f>0是什么？
3 强化模型
各向同性强化：假设屈服面均匀膨胀，没有崎 变和移动，此时屈服面可表达为
f ( ij , k ) f ( ij ) k ( ) 0
强化模型实际上表示后继屈服面的变化规律， 即如何随硬化参数而变。强化参数可以取累积 塑性变形。
e d ij
1 1 d ij dsij d kk ij dsij 2G 9K 对刚塑性材料，不计弹性部分，为 d ij dsij 此为Levy Mises方程
d的确定 理想塑性
对理想塑性J 2材料，有 2 2 2 sij sij e2 y (1) 3 3 两边求导，有 2 sij dsij 0 (2) 偏应变增量可写为 1 dsij dsij (3) 2G 上式两边同乘以sij并求和有 deij sij deij 1 sij dsij dsij sij dsij sij 2G ( 4)

塑性理论课件-塑性变形时的应力应变关系

塑性理论课件-塑性变形时的应力应变关系
下一頁 返回
3、如果從初始狀態先加純剪應力通過 屈服點B到達D點，這時的應力和應變見表 5.1的第3行。
4、如同樣經後繼屈服軌跡裏面的任意 路線變載到F點，則應力應變見表5.1第4行。
5、如果從初始狀態沿真線OF`F到達F 點，則應力和應變見表5.1第5行，這時主軸 重合。
下一頁 返回
上述的第1、3、5種加載路線就是簡單加載。 由表中可看出，同樣的一種應力狀態σf、τf，由於 加載路線不同，就有好幾種應變狀態（如C、D點 應變）；同樣，一種應變狀態（如εc），也可有 幾種應力狀態（如C、F點應力），而且應力應變 主軸不一定重合。從上述簡單的例子中，我們可 以看到，離開加載路線來建立應力與全量塑性應 變之間的普遍關係是不可能的。因此，一般情況 下只能建立起應力和應變增量之間的關係爭然後 根據具體的加載路線，具休分析。另一方面，我 們從上述例子中也看到，在簡單加載的條件下， 應力和應變的主軸重合，而且它們之間有對應關 係，因此可以建立全量理論。
下一頁 返回
另一方面，從工程角度來看，對於一 些繁雜的問題，那怕是能給出定性結果也 很可貴，具體的定量問題可以從實驗中進 一步探索（由於如摩擦條件等數學模型還 未給出，要精確計算也很難辦到）。鑒於 壓力加工理論中關於成形規律闡述上存在 的一些問題，吸取了增量理論及全量理論 的共同點，提出了應力應變順序對應規律， 並使該規律的闡述逐漸簡明和便於應用。 現簡述如下：
返回
5.2增量理論（流動理論） 一、列維-密席斯方程 二、普朗特-勞斯方程
返回
一、列維-密席斯方程
列維-密席斯方程適用條件：
（1)材料是理想剛塑性材料，即彈性應變增 量為零，塑性應變增量就是總應變增量；
（2）材料符合密席斯屈服準則，即 s

(完整版)弹塑性力学作业(含答案)(1)

(完整版)弹塑性力学作业(含答案)(1)

第二章 应力理论和应变理论2—3．试求图示单元体斜截面上的σ30°和τ30°（应力单位为MPa ）并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时，其符号及正负值应作何修正。

解：在右图示单元体上建立xoy 坐标，则知 σx = -10 σy = -4 τxy = -2 （以上应力符号均按材力的规定）代入材力有关公式得： 代入弹性力学的有关公式得： 己知 σx = -10 σy= -4 τxy = +2由以上计算知，材力与弹力在计算某一斜截面上的应力时，所使用的公式是不同的，所得结果剪应力的正负值不同，但都反映了同一客观实事。

2—6. 悬挂的等直杆在自重W 作用下（如图所示）。

材料比重为γ弹性模量为 E ，横截面面积为A 。

试求离固定端z 处一点C 的应变εz 与杆的总伸长量Δl 。

解：据题意选点如图所示坐标系xoz ，在距下端（原点）为z 处的c 点取一截面考虑下半段杆的平衡得：c 截面的内力：N z =γ·A ·z ；c 截面上的应力：z z N A zz A Aγσγ⋅⋅===⋅；所以离下端为z 处的任意一点c 的线应变εz 为：z z z E Eσγε==；则距下端（原点）为z 的一段杆件在自重作用下，其伸长量为：()22z z z z z z z z y zz l d l d d zd EEEγγγε=⎰⋅∆=⎰⋅=⎰=⎰=ooooV ；显然该杆件的总的伸长量为（也即下端面的位移）：()2222ll A l lW ll d l EEAEAγγ⋅⋅⋅⋅⋅=⎰∆===oV ；（W=γAl ） 2—9.己知物体内一点的应力张量为：σij =50030080030003008003001100-⎡⎤⎢⎥+-⎢⎥⎢⎥--⎣⎦应力单位为kg ／cm 2 。

试确定外法线为n i（也即三个方向余弦都相等）的微分斜截面上的总应力n P v、正应力σn 及剪应力τn 。

《弹塑性力学》第四章 应力应变关系(本构方程)-精品文档42页

《弹塑性力学》第四章 应力应变关系(本构方程)-精品文档42页
ji,j+ fi = 0 ij =( ui,j+ uj,i)/2
28.09.2019
2
第四章 应力应变关系（本构方程）
共9个方程，但需确定的未知函数共15个：
ui，ij=ji， ij=ji，
还需要根据材料的物理性质来建立应力与 应变间的关系：
ij = ji = fij ( kl )
Wijij
——W为
的函数。
ij
28.09.2019
11
§4-1 应变能、应变能密度与弹性材料的
本构关系
因为W只取决于弹性体的初始应变状态和最 终应变状态，与变形过程（加载路线）无关，
所以W 为它的全微分
W

W
ij
ij
28.09.2019
12
§4-1 应变能、应变能密度与弹性材料的
时刻达到 t +t：位移有增量 uuiei
应变增量 ijeiej 外力功增量：A Vfu d V S F u d S
28.09.2019
8
§4-1 应变能、应变能密度与弹性材料的
A 本构f关u 系d VF u d ：函S 数增量
则 [C] 为对称矩阵 [C]= [C]T。
28.09.2019
19
§4-2 线弹性体的本构关系
2.1 各向异性材料 Eijkl 的独立系数为21个——材料为各向
异性线弹性材料。
*对各向异性材料的本构关系可见，剪应 变引起正应力，正应变也产生剪应力。 弹性材料性质一般都具有某些对称性， 利用对称可进一步简化 [C] 中系数。
V
S
Vfiuid V sF iuid SU V Wd
应变能增量A 中有体积分和面积分，利用

弹性与塑性力学基础-第五章屈服准则与塑性应力应变关系

弹性与塑性力学基础-第五章屈服准则与塑性应力应变关系

0
m

0 0 m
Uv
1 3 ( m m m m m m ) m m 2 2 1 m ( 1 2 3 ) 3
1 m ( 1 2 3 ) 3
弹性与塑性 力 学 基 础
第五章 屈服准则与塑性应力应变关系
积之和的一半(主坐标系中)
U
1 ( 1 1 2 2 3 3 ) 2
1 0 ij T 0 2 0 0
0 0 3
1 0 ij T 0 2 0 0
0 0 3
弹性与塑性 力 学 基 础
第五章 屈服准则与塑性应力应变关系
§5-2 米塞斯屈服准则
5.2.1 米塞斯屈服准的物理意义 米塞斯屈服准则 5.2.2
由广义虎克定律
1
1 2 [ 2 ( 1 3 )] E 1 3 [ 3 ( 1 2 )] E
式中， 为波桑系数，于是可得
弹性与塑性 力 学 基 础
第五章 屈服准则与塑性应力应变关系
§5-2 米塞斯屈服准则
5.2.1 米塞斯屈服准的物理意义 米塞斯屈服准则 5.2.2
单位体积变化位能Uv确定
取应力球张量及应变球张量
m T0
由此得
0
m

0 0 m
m T0
§5-10 全量理论
5.10.1 问题的背景及引出 5.10.2 亨盖理论(1924年) 5.10.3 那达依理论(1937年) 5.10.4 伊留申理论(1943年) 5.10.5 全量理论的问题与发展
弹性与塑性 力 学 基 础

塑性力学复习题

塑性力学复习题

塑性力学复习题一、填空题1．塑性变形不仅与当前的应力状态有关，还和（）有关。

2．对一般金属，体积应变完全是（）的，静水压力不产生（）。

它对屈服极限的影响（）。

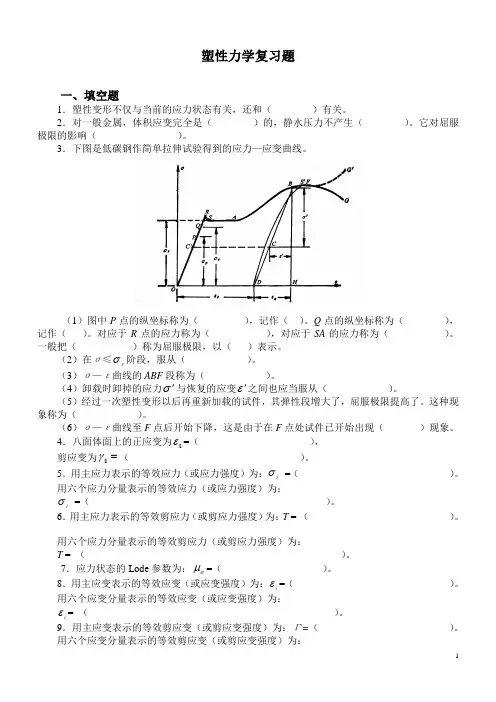
3．下图是低碳钢作简单拉伸试验得到的应力—应变曲线。

（1）图中P点的纵坐标称为（），记作（）。

Q点的纵坐标称为（），记作（）。

对应于R点的应力称为（），对应于SA的应力称为（）。

一般把（）称为屈服极限，以（）表示。

σ阶段，服从（）。

（2）在σ≤s（3）σ—ε曲线的ABF段称为（）。

（4）卸载时卸掉的应力σ'与恢复的应变ε'之间也应当服从（）。

（5）经过一次塑性变形以后再重新加载的试件，其弹性段增大了，屈服极限提高了。

这种现象称为（）。

（6）σ—ε曲线至F点后开始下降，这是由于在F点处试件已开始出现（）现象。

ε=（），4．八面体面上的正应变为8γ（）。

剪应变为=8σ=（）。

5．用主应力表示的等效应力（或应力强度）为：i用六个应力分量表示的等效应力（或应力强度）为：σ=（）。

i6．用主应力表示的等效剪应力（或剪应力强度）为：T = （）。

用六个应力分量表示的等效剪应力（或剪应力强度）为：T = （）。

μ=（）。

7．应力状态的Lode参数为：σε=（）。

8．用主应变表示的等效应变（或应变强度）为：i用六个应变分量表示的等效应变（或应变强度）为：ε= （）。

i9．用主应变表示的等效剪应变（或剪应变强度）为：Γ=（）。

用六个应变分量表示的等效剪应变（或剪应变强度）为：Γ=（ ）。

10．表示应变状态特征的Lode 参数为：εμ=（ ）。

11．第一应力不变量为：1I =（ ）=（ ）。

第二应力不变量为：2I =（ ）=（ ）。

第三应力不变量为：3I =（ ）=（ ）。

12．第一应变不变量为：1I '=（ ）=（ ）。

第二应变不变量为：2I '=（ ）=（ ）。

第三应变不变量为：='3I （ ）=（ ）。

13．应力偏张量的第一不变量为：=1J （ ）。

第五节塑性成形时应力应变关系-2013年编辑

第五节塑性成形时应力应变关系-2013年编辑

21
由于加载路线不同，同一种应力状态可以对
应不同的应变状态; 而且应力与应变主轴不一定重合。
同一种应变状态，也可以对应几种应力状态，
因此，一般情况下只能建立起应力和应变增 量之间的关系，仅在简单加载的条件下，应力主
轴与应变主轴重合，才可以建立全量关系。
22
τ D B I
初始屈服轨迹
F ( f , f )
及
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
应 力 应 变 关 系
上式表明：应变莫尔圆与应力莫尔圆几何相似，且成 正比。
13
弹性变形时的应力应变关系的特点
20
清是哪条路径下的σ-ε关系。
加载路线A→C，应力为σc ，而应变为ε1=εc ， ε2=ε3 = -εc/2。 若卸载至E点，由于塑性变形不可逆，E点应变仍然为C 点应变，再施加切应力E→F，此时应力为σF、τF，而F 点应变仍然为C点应变，因此，F点C点应变状态相同(即 ε1=εc，ε2=ε3=-εc/2。)，而应力不同，不一一对应。
§应力与应变完全成线性关系。 §应力主轴与全量应变主轴重合
§弹性变形是可逆的，与应变历史 （加载过程无关），应力与应变 之间存在统一的单值关系.
§弹性变形时，应力张量使物体产 生体积变化，泊松比小于0.5.
1 2 m m 0,即： 1 2 0， 0.5 E
14
5.2
同理

'
y
1 ' y 2G
' ij

'
z
1 ' z 2G

第十七章 塑性应力应变关系(本构关系)

第十七章 塑性应力应变关系(本构关系)

• 广义胡克定律的比例式：
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
弹性应力应变关系的特点
• 应力与应变完全呈线性关系，应力主轴与应变主 轴重合。 • 弹性变形是可逆的，应力与应变单值对应。 • 弹性变形时，应力球张量使物体产生体积变化， 泊松比υ＜0.5

' y

z

' z

xy
xy

yz
yz

zx
zx
d
d 3 2

x y
z x d x y y z z x 1 2 2 3 3 1 d 1 2 2 3 3 1
• 流动理论是描述材料处于塑性状态时，应 力与应变增量或应变速率之间关系的理论。 该理论针对是加载过程的任一瞬间，认为 应力状态确定的不是全量应变，而是该瞬 时的应变增量，从而撇开了加载路线和加 载历史的影响。
Levy—Mises方程
' ' ij ij d
x

' x

y
第五节 塑性应力应变关系（本构关系）
• 一、弹性应力应变关系———Hooke’s Law 对于各向同性材料，有广义虎克定律：
1 1 x y z ; xy xy E 2G 1 1 y y x z ; yz yz E 2G 1 1 z z x y ; zx zx E 2G
• 弹塑性
塑性应变

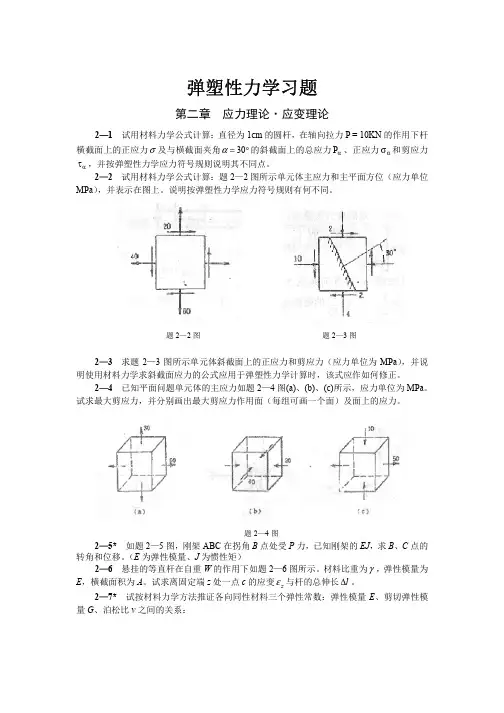
弹塑性力学习题集 很全有答案

弹塑性力学习题集 很全有答案
3—8 有一处于二向拉伸应力状态下的微分体（ σ1 ≠ 0, σ 2 ≠ 0, σ 3 = 0 ），其主应变
为 ε1 = 1.7 ×10−4 ， ε 2 = 0.4 ×10−4 。已知ν = 0.3，试求主应变 ε 3 。 3—9 如题 4—9 图示尺寸为 1×1×1cm 的铝方块，无间隙地嵌入——有槽的钢块中。
2—9 已知一点的应力张量为：
50 50 80
σ ij
=
0 − 75MPa
(对称)
− 30
试求外法线
n
的方向余弦为： nx
=
1 2
，ny
=
1 2
， nz
=
1 2
的微斜面上的全应力 Pα
，正
应力 σ α 和剪应力τ α 。
2—10 已知物体的应力张量为：
50 30 − 80
σ ij
=
0 − 30MPa
主应变的表达式。 2—41* 已知如题 2—41 图所示的棱柱形杆在自重作用下的应变分量为：
εz
=
γz E
,
εx
=εy
=
− νγz E
;
γ xy = γ yz = γ zx = 0;
试求位移分量，式中 γ 为杆件单位体积重量，E、ν 为材料的弹性常数。
2—42 如题 2—42 图所示的圆截面杆扭转时得到的应变分量为：ε x = ε y = ε z = γ xy = 0,
2
3
各弹性常数的物理意义。
3—4* 如设材料屈服的原因是形状改变比能（畸形能）达到某一极值时发生，试根据
单向拉伸应力状态和纯剪切应力状态确定屈服极限 σ s 与τ s 的关系。 3—5 试依据物体单向拉伸侧向不会膨胀，三向受拉体积不会缩小的体积应变规律来

工程塑性理论应力应变关系

工程塑性理论应力应变关系

2
E
m
y
m
1 E
y
z
x
1 2
E
m
z
m
1 E
z
x y ｛｝
1
2
E
m
x m , y m ,
x y
x m , y m ,
xy y z
xyzymmmm
,
z z m
z
z
m
Gz 2z1Em
x
1 2G
x
,
y
1 2G
y
,
z
1 2G
z
,
xy
yx
1 2G
xy
即应变增量张量就是应变增量偏张量。
在上述假设基础上，可假设应变增量与 应力偏张量成正比，即
d ij ij d
d x d y d z d xy d yz d zx d x m y m z m xy yz zx
式中：dλ—正的瞬时常数，在加载的不同 瞬时是变化的，在卸载时，dλ=0。
d ij ij d
d x x m d
x
x
y
3
z
d
2 3
d
x
1 2
y
z
d x
2 3
d
x
1 2
y
z
,
d y
2 3
d
y
1 2
z
x ,
d z
2 3
d
z
1 2
x
y
,
d xy
xy
d
d yz yzd
d zx zx d
将上式正应变两两相减，并写出切应变公式：
yz
2G
zx

3-5 应力应变关系(本构关系)

3-5 应力应变关系(本构关系)

例题：
有一立方块金属，分别在x、y和z方向 上作用200MPa、 200MPa和250MPa的压应 力，试求金属块的体积变化率（设E＝ 2.07×105MPa，ν＝0.3）
金属塑性成形原理
z 250MPa
200MPa
x
200MPa
y
解：
各方向应力为：σx＝－200MPa、 σy ＝－200MPa、 σz ＝－250MPa，
1 2G
ij
该式表明：应变偏张量与应力偏张量成正比，表明物体形状的改变只是
由应力偏张量引起的。
金属塑性成形原理
所以，广义虎克定律可写成张量形式：
ij
ij
ijm
1 2G
ij
1 2
E
ij m
广义虎克定律还可以写成比例及差比的形式
比例形式：
x y z yz zx xy 1 x y z yz zx xy 2G
金属塑性成形原理
3.5： 金属塑性变形的力学基础 ——本构关系
金属塑性成形原理
内容提纲
一、弹性变形时应力应变关系 二、塑性变形时应力应变关系的特点 三、增量理论 四、全量理论 五、应力应变顺序对应规律 六、屈服椭圆的应力分区及与成形时工作尺寸变化关系 小结
金属塑性成形原理
第五节 塑性变形时应力应变关系（本构关系）
[( x
y )2
( y
z )2
( z
x )2
6(
2 xy
2 yz
2 xz
)]
E i
i 称为弹性应变强度，且：
i
1
21
[பைடு நூலகம் x
y )2
( y
z )2
( z
x )2

弹塑性力学大题

弹塑性力学大题

已知某材料在纯剪作用下应力—应变关系如图所示，弹性剪切模量为G ，Poisson 比为ν，剪切屈服极限为s τ，进入强化后满足const G d d ==,/γτ。

若采用Mises 等向硬化模型，试求（1）材料的塑性模量（2）材料单轴拉伸下的应力应变关系。

解：（1）因为τττγ221232*123121J d J h d p⎥⎥⎦⎤⎢⎢⎣⎡= 所以τγd hd p *3*1=,3*3G d d h p==γτ （2） 弹性阶段。

因为)1(2υ+=EG ，所以)1(2υ+=G E 由于是单轴拉伸，所以εσE = 塑性阶段。

ijp ij fd d σλε∂∂= 1111)1(σσσε∂∂∂∂=fd f h d kl kl p解：在板的固定端，挠度和转角为零。

显然：()0)(b y ==±=±=ωωa x 满足0)(2)(2)(222221=-⋅-=∂∂±=b y x a x C xa x ω故222222111)()(b y a x C w C w --==满足所有的边界条件。

02))((2)y(222221=⋅--=∂∂±=y b y a x C b y ω2、用Ritz 法求解简支梁在均布荷载作用下的挠度（位移变分原理）步骤：（1）设挠度的试验函数 w (x ) = c 1x (l -x )+c 2x 2(l 2-x 2)+…显然，该挠度函数满足位移边界w (0) =0，w (l ) = 0。

（2）求总势能()⎰⎰-''=+=∏l 002qwdx dx w EI 21lV U 仅取位移函数第一项代入，得()()⎰⎥⎦⎤⎢⎣⎡---=∏l 0121dxx l qx c c 2EI 21（3）求总势能的极值EI24ql c 0c 211==∂∏∂ 代入挠度函数即可1.假定矩形板支承与承受荷载如图所示， 试写出挠度表示的各边边界条件： 解：简支边OC 的边界条件是：()00==y ω()0022220)(M xy D M y y y -=∂∂+∂∂-===ωνω自由边AB 的边界条件是：()0)(2222=∂∂+∂∂===b x by y x y M ωνω，()()q y x y D V by b y y -=⎪⎪⎭⎫ ⎝⎛∂∂∂-+∂∂-===23332ωνω两自由边的交点B ：()0,===b y a x ω()B by a x xy R M ===,2是B 点支座的被动反力。

塑性应力应变关系

塑性应力应变关系

习题
7-1 工程法求解变形力的原理是什么？有何特点？
7-2 工程法的基本要点和基本假设有哪些？
7-3 工程法求解的基本步骤如何？
7-4 何谓多余应变与多余功？
7-5 在锻压机上将φ50×500mm 的LD 2铝合金圆柱体平锤横向锻压成断面积相等
的方坯，若终锻温度（420℃）下的T σ=40MPa ，使用油基石墨作润滑剂时的摩擦系数f =0.3，所需锻压力为多少？若不进行润滑的锻压力又是多少？ 7-6 试用工程法导出润滑砧面平锤压缩圆盘时的平均单位压力公式。

7-7 不变薄拉深将t 0=0. 8mm 的纯铝圆片生产内径φ10mm 、深12mm 的筒形件，
问圆片的直径应为多少？若拉深时的压力边Q =200MPa ，f 1=f 2=0.1, r d =5mm, δ=1. 2mm ，平均变形抗力80=f K MPa ，试问拉深至h =8mm 时的拉深力为多少？
7-8 某厂有1600吨铝材热挤压机一台，常用挤压筒为φ170mm ，铝锭规格为φ162×450mm ，为了保证挤压制品的组织性能合格，最小挤压比不得低于8；以及正常使用的挤压机吨位为80%。

试问当不计挤压模孔定径带部分的摩擦阻力时，该挤压机用单孔模挤压的最小和最大圆棒直径为多少？计算时取45=T σMPa ，︒=60α。

弹塑性力学 应力和应变之间的关系

弹塑性力学 应力和应变之间的关系

我所认识的应力和应变之间的关系在单向应力状态下，理想弹性材料的应力和应变之间的关系是满足胡克定律的一一对应的关系。

在三维应力状态下描述一点处的应力状态需要9个分量，相应的应变状态也要用9个应变分量来表示。

对于一个具体的理想弹性体来讲，如果在三维应力状态下，应力与应变之间仍然有线性一一对应关系存在，则称这类弹性体为线性弹性体。

所谓各向弹性体，从力学意义上讲，就是弹性体内的每一点沿各个方向的力学性质都完全相同的。

这类线性弹性体独立的唐兴常数只有两个。

各向同性体本构关系特点：1.主应力与主应变方向重合。

2.体积应力与体积应变成比例。

3.应力强度与应变强度成比例。

4.应力偏量与应变偏量成比例。

工程应用中，常把各向同性弹性体的本构方程写下成11()11()11()x y z xy xy y x z yz yz z y x xz xz E G E G E G εσμσσγτεσμσσγτεσμσσγτ⎧⎡⎤=-+=⎣⎦⎪⎪⎪⎡⎤=-+=⎨⎣⎦⎪⎪⎡⎤=-+=⎪⎣⎦⎩，式中分别为弹性模量、泊松比和剪切模量。

在E G μ、、这三个参数之间，实际上独立的常量只有两个，它们之间存在关系为()21E G μ=+。

屈服条件:弹性和塑性的最主要区别在于变形是可以恢复。

习惯上，根据破坏时变形的大小把工程材料分为脆性材料和塑性材料两类。

对于加载过程如图1OA: 比例阶段；线性弹性阶段AB: 非弹性变形阶段 BC ： 初始屈服阶段 s σσ≤ CDE ：强化阶段；应变强化硬化阶段EF ： 颈缩阶段；应变弱化，软化阶段s σσ≥ C 点为初始屈服点具有唯一性。

在应力超过屈服应力后，如果在曲线上任意一点D 处卸载，应力和应变之间将不再遵循原有的加载曲线规律，而是沿一条接近平行于OA 的直线DO ’变化，直到应力下降为零，这时应变并不为零，即有塑性应变产生。

如果用OD ’表示总应变ε，O ’D ’表示可以恢复的弹性应变eε，OO ’表示不能恢复的塑性应变p ε，则有e p εεε=+，即总应变等于弹性应变加上塑性应变。

弹塑性力学习题集_很全有答案_

弹塑性力学习题集_很全有答案_

σ y = cx + dy − γy , τ xy = − dx − ay ，其它应力分量为零。试根据
直边及斜边上的边界条件，确定常数 a、b、c、d。 2—16* 已知矩形截面高为 h， 宽为 b 的梁受弯曲时的正 My 12 M 应力 σ z = = y， 试求当非纯弯时横截面上的剪应力公 J bh 3 式。 （利用弹塑性力学平衡微分方程）
题 2—15 图
12 6 0 2—17 已知一点处的应力张量为： σ ij = 6 10 0 MPa ，试求该点的最大主应力及 0 0 0 其主方向。 2—18* 在物体中某一点 σ x = σ y = σ z = τ xy = 0 ，试以 τ yz 和 τ zx 表示主应力。
3—1
为 ε 1 = 1.7 × 10 −4 ， ε 2 = 0.4 × 10 −4 。已知ν = 0.3，试求主应变 ε 3 。
3—9 如题 4—9 图示尺寸为 1×1×1cm 的铝方块，无间隙地嵌入——有槽的钢块中。 设钢块不变形，试求：在压力 P = 6KN 的作用下铝块内一点应力状态的三个主应力及主应 变，铝的弹性常数 E=70Gpa，ν = 0.33。 3—10* 直径 D = 40mm 的铝圆柱体， 无间隙地放入厚度为 δ = 2mm 的钢套中， 圆柱受
v = b0 + b1 x + b2 y + b3 z w = c 0 + c1 x + c 2 y + c3 z
式中 a 0 L , a1 L , a 2 L 为常数，试证各点的应变分量为常数。 2—29 设已知下列位移，试求指定点的应变状态。
(1) u = (3x 2 + 20) × 10 −2 , v = (4 yx) × 10 −2 ，在（0，2）点处。 (2) u = (6 x 2 + 15) × 10 −2 , v = (8 zy ) × 10 −2 , w = (3z 2 − 2 xy) × 10 −2 ，在（1，3，4）点处。 2—30 试证在平面问题中下式成立： εx + εy =ε′ x + ε′ y

金属塑性变形理论习题集

金属塑性变形理论习题集

《金属塑性变形理论》习题集第一部分：塑性加工力学第一章 应力状态分析1． 金属塑性加工中的外力有哪几种？其意义如何？2． 为什么应力分量的表达需用双下标？每个下标都表示何物理意义？ 3． 已知应力状态如图1-1所示，写出应力分量，并以张量形式表示。

4． 已知应力状态的六个分量7-=x σ，4-=xy τ，0=y σ，4=yz τ，8-=zx τ，15-=z σ(MPa)，画出应力状态图，写出应力张量。

5． 作出单向拉伸、单向压缩、三向等值压缩、平面应力、平面应变、纯剪切应力状态的应力Mehr 圆。

图1-1⎪⎪⎪⎭⎫⎝⎛------=1548404847σT xy z6． 已知应力状态如图1-2所示，当斜面法线方向与三个坐标轴夹角余弦31===n m l 时，求该斜面上的全应力S 、全应力在坐标轴上的分量x S 、y S 、z S 及斜面上的法线应力n σ和切应力n τ。

7． 将下列应力状态用单元体表示。

（1）⎪⎪⎪⎭⎫⎝⎛---=6040504050705070100σT N/mm 2 （用直角坐标系）（2）⎪⎪⎪⎭⎫ ⎝⎛-=2007090701000900120σT N/mm 2 （用柱面坐标系）8． 单元体上各面所作用的应力分量如图1-3所示。

根据应力分量的正负规定，在相应的圆圈内填上适当的“+”、“－”。

9． 何谓求和约定？什么是哑标？什么是自由标？y±z±图1-3图1-210． 已知jn m nim ij βσασ='，找出哑标和自由标，并写出12σ'的展开式。

33332333232233132132322332222232122131312331212231112123βσαβσαβσαβσαβσαβσαβσαβσαβσασ++++++++='11． 任举一例利用求和约定对公式进行展开和合并。

12． 你是如何理解“应力张量”这一概念的？试用自己的语言描述之。

塑性变形时的应力应变关系

塑性变形时的应力应变关系

x
1 2
y z
;
xy xy
y
2
3
y
1 2
z
x ;
yz yz
z
2 3
z
1 2
x y
;
zx zx
例3-10 塑性应力应 变关系应用
受内压薄壁圆筒屈服，
半径r ，内压p，材料屈服应力S ，求应变增量各分量的比值 。
p 0;
p2r 2t
pr ; t
z
p r2 2r t
d ?
dx d y
2
x y
2 d 2
d y dz
2
y z
2 d 2
d z d x 2 z x 2 d 2
6d xy2 6 xy2d 2 6d yz2 6 yz2d 2 6d zx2 6 zx2d 2
dx dy
2
d y dz
2
dz dx
2 6 d xy2 d yz2 d zx2
2 yz
2 zx
1 E
2 1
x y
2
y z
2
z x
2 6
2 xy
2 yz
2 zx
i
1
2 1
x y
2
y z
2
z x
2 6
2 xy
2 yz
2 zx
应变强度
i
2
3
1
Ei
弹性变形时应力应变关系的特点
应力与应变成线性关系，是一一对应的关系；
弹性变形是可逆的，加载与卸载的规律完全相同；
材料是理想刚塑性材料，即 diej 0 ，dij dijp ；
材料符合密席斯屈服准则，即 S ；
每一加载瞬间，应力主轴与应变增量主轴重合； 塑性变形时体积不变，即dx dy dz d1 d2 d3 0 和 dij dij； 应变增量与应力偏量成正比（列维－密席斯方程）。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。