初一数学答案doc20132014学年度第二学期南

南京市高淳区2013～2014学年度第二学期期末质量调研检测七年级数学试卷一、选择题（每小题2分，共16分．请将正确答案的字母代号填在下面的表格中）1．某种花粉颗粒的直径约为32微米（1微米=610-米），则将32微米化为米并用科学计数法表示为( ▲ )A ．6102.3-⨯米 B ．61032-⨯米 C ．5102.3-⨯米 D ．51032.0-⨯米 2．下列计算正确的是( ▲ )A ．6332a a a =+B ．623a a a =⋅C ．326a a a =÷ D ．623)(a a =3．在下列长度的四根木棒中，能与两根长度分别为cm 4和cm 9的木棒构成一个三角形的是( ▲ ) A ．cm 4 B ．cm 5 C ．cm 9 D ．cm 134．不等式组的解集在数轴上可以表示为( ▲ )A ．B ．C ．D ．5．如图，能判定EC ∥AB 的条件是( ▲ ) A ．∠B ＝∠ACE B ．∠A ＝∠ECD C ．∠B ＝∠ACBD ．∠A ＝∠ACE6．下列算式中，结果为224y x -的是( ▲ )A.2)2(y x - B.)2)(2(y x y x --+- C.)2)(2(y x y x +- D. )2)(2(y x y x +--7．下列命题：①同旁内角互补；②若1<n ，则012<-n ；③直角都相等；④相等的角是对顶角．其24357x x -⎧⎨-⎩＞≤DCBEA(第5题)中，真命题的个数有( ▲ ) A ．1个B ．2个C ．3个D ．4个8．若)4)(2(--=x x P ，2)3(-=x Q ，则P 与Q 的关系为( ▲ ) A ．P ＝QB ．P >QC ．P <QD ．P 与Q 的大小无法确定二、填空题（每小题2分，共20分）9．=-0)2( ，=-121( ．10. 命题“垂直于同一直线的两直线平行”的条件是 ， 结论是 .11．已知21x y =⎧⎨=-⎩是二元一次方程12=+my x 的一个解，则m ＝ ．12．如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2. 若∠3=40°，则∠4等于 ．13．若2-=+b a ，4=-b a ，则=-22b a .14．命题“直角三角形的两个锐角互余”的逆命题为： . 15．一个多边形每个外角的大小都是其相邻内角大小的21，则这个多边形是 边形． 16. 课本上，公式 (a －b )2＝a 2－2ab ＋b 2 是由公式 (a ＋b )2＝a 2＋2ab ＋b 2 推导得出的．已知 (a ＋b )4＝a 4＋4a 3b ＋6a 2b 2＋4ab 3＋b 4，则 (a －b )4＝ ．17．如图，五边形ABCDE 中，AB ∥CD ，∠1、∠2、∠3分别是∠BAE 、∠AED 、∠EDC 的外角，则∠1+∠2+∠3等于 ．18．如图，将面积为5的△ABC 沿BC 方向平移至△DEF 的位置，平移的距离是边BC 长的两倍，那么图中的四边形ACED 的面积为 ．a b1 4c 3 2 （第12题）ABCD23 E三、解答题（本大题共10小题，共64分） 19．计算：(1) （3分）232)()(a a -÷；(2) （4分）)(3))(2(b a a b a b a +-++.20．（ 4分）因式分解：n mn n m 8822+-．21．（5分）解方程组 ⎩⎨⎧=-=+.132,42y x y x①②22．（ 5分）解不等式 2321xx <-- ．23．（5分）把下面的证明过程补充完整.已知：如图，AD ⊥BC 于D ，EF ⊥BC 于F ，交AB 于G ，交CA 延长线于E ，∠1=∠2． 求证：AD 平分∠BAC ．证明：∵ AD ⊥BC ，EF ⊥BC （已知）∴90=∠=∠EFC ADC ( ) ∴AD ∥EF （ ）. ∴BAD ∠=∠1（ ） ________ = _______（两直线平行，同位角相等） ∵ 21∠=∠（已知）∴ _________ ，即AD 平分∠BAC （ ）.24．（6分）小明有1元和5角的硬币共15枚，其中1元的硬币不少于2枚，这些硬币的总币值少于10元.问小明可能有几枚1元的硬币？（第23题）25．（8分）如图，在ABC ∆中，C B ∠>∠,BC AD ⊥,垂足为D ,AE 平分BAC ∠． （1）已知60=∠B ，30=∠C ，求DAE ∠的度数； （2）已知C B ∠=∠3，求证：C DAE ∠=∠.26．（ 7分）已知关于x ，y 的方程组325x y a x y a-=+⎧⎨+=⎩的解x ，y 都为正数．（1）求a 的取值范围； (2)化简2a a --．（第25题）AB D E C27.（8分）在四边形ABCD 中，若DC AB //,且BC AD //,则称四边形ABCD 为平行四边形（即两组对边分别平行的四边形叫做平行四边形）.（1）已知：如图（1），四边形ABCD 为平行四边形，求证：D B ∠=∠；（2）已知：如图（2），四边形EFGH 中,HG EF //, G E ∠=∠，求证：四边形EFGH 为平行四边形.ADCB(第27题(2）)EHGF(第27题(1）)28．（9分）某商店经营甲、乙两种商品，其进价和售价如下表：已知该商店购进了甲、乙两种商品共160件．（1）若商店在销售完这批商品后要获利1000元，则应分别购进甲、乙两种商品各多少件?（2）若商店的投入资金少于4300元，且要在售完这批商品后获利不少于1250元，则共有几种购货的方案? 其中，哪种购货方案获得的利润最大？2013～2014学年度第二学期期末质量调研检测试卷七年级数学参考答案一、选择题（每小题2分，共16分．请将正确答案的字母代号填在下面的表格中）二、填空题（每小题2分，共20分）9.1，2 10. 两条直线垂直于同一直线，这两条直线平行 11.3 12.70° 13.-8 14. 两个锐角互余的三角形是直角三角形 15.六 16. a 4-4a 3b ＋6a 2b 2-4ab 3＋b 4 17. 180° 18.15 三、解答题（本大题共10小题，共64分）19．（1）原式26a a ÷= ………………………………2分4a = ………………………………3分（2）原式ab a b ab a 3323222--++= ………………………3分 2222b a +-= ………………………4分20．原式)44(22+-=m m n ………………………2分 2)2(2-=m n ………………………4分 21.解：②-①×2，得 77-=-y1=y ………………………3分 把1=y 代入①得 2=x ………………………4分∴原方程组的解为⎩⎨⎧==12y x ………………………5分22.解：x x 3)2(26<-- ………………………1分 x x 3426<+- ………………………2分 1032-<--x x ………………………3分 105-<-x ………………………4分 2>x ………………………5分 23. 垂直定义； ………………………1分 同位角相等，两直线平行；………………………2分两直线平行，内错角相等；………………………3分 D A C ∠=∠2； ………………………4分 D A C B A D ∠=∠,角平分线定义………………………5分24.解：设小明有1元的硬币x 枚，则5角硬币有)15(x -枚. ……………1分 由题意得：⎩⎨⎧<+-≥10)15(5.02x x x ………………………3分解得：52<≤x ………………………4分x 的整数值为2、3、4. ………………………5分答：小明1元的硬币可能有2、3或4枚. ………………………6分 25.（1）在△ABC 中,∠BAC =180°－∠B －∠C =90°……………………1分 ∵AE 平分∠BAC ∴∠BAE =21∠BAC =45° ………………………2分 ∵AD ⊥BC∴∠BAD=90°－∠B =30° ………………………3分 ∴ ∠DAE =∠BAE －∠BAD =15° ………………………4分 （2）在△ABC 中, ∵∠B =3∠C∴ ∠BAC =180°－∠B －∠C =180°－4∠C ………………………5分 ∵AE 平分∠BAC ∴∠BAE=21∠BAC =90°－2∠C ………………………6分 ∵AD ⊥BC∴∠BAD =90°－∠B =90°－3∠C ………………………7分 ∴ ∠DAE =∠BAE －∠BAD =(90°－2∠C )－(90°－3∠C )=∠C即C DAE ∠=∠ ………………………8分26.（1）解方程组得⎩⎨⎧-=+=212a y a x ………………………2分∵ 方程组的解x ，y 都为正数∴⎩⎨⎧>->+02012a a ………………………4分解得2>a∴a 的取值范围是2>a ………………………5分 （2）由（1）得2>a ，故02<-a∴原式)2(--=a a ………………………6分2= ………………………7分 27. （1）∵四边形ABCD 为平行四边形∴DC AB //,BC AD // ………………………2分∴∠A +∠D =180°, ∠A +∠B =180°（两直线平行，同旁内角互补）∴∠B ﹦∠D (同角的补角相等) ………………………4分 （2）∵EF //HG (已知)∴∠E +∠H =180°（两直线平行，同旁内角互补）………………………5分 ∵∠E ﹦∠G∴∠G +∠H =180°(等量代换) ………………………6分 ∴EH //FG (同旁内角互补, 两直线平行) ………………………7分 ∴四边形EFGH 为平行四边形(平行四边形定义) ………………………8分28.（1）设商店甲、乙两种商品分别购进了x 件、y 件， 由题意得⎩⎨⎧=+=+1000105160y x y x ………………………2分解得⎩⎨⎧==40120y x答：商店甲、乙两种商品分别购进了120件、40件. ………………………4分 （2）设商店甲商品购进了z 件，则乙商品购进了（160-z ）件， 由题意得： ⎩⎨⎧≥-+<-+1250)160(1054300)160(3515z z z z ………………………6分解得7065≤<z∴z 的整数值为66,67,68,69,70. ………………………7分 即共有5种购货的方案：①甲购进66件、乙购进94件，②甲购进67件、乙购进93件，③甲购进68件、乙购进98件，④甲购进69件、乙购进91件，⑤甲购进 70件、乙购进90件. ……………………8分 其中，购货方案①获得的利润最大. ……………………9分。

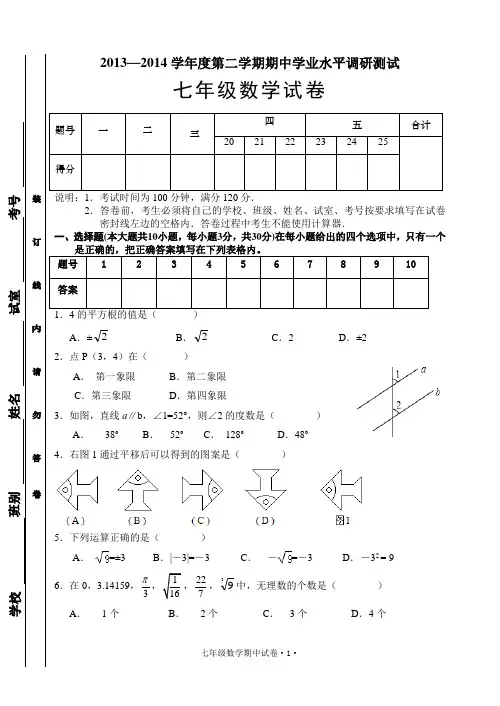
2013—2014学年度第二学期期中学业水平调研测试七年级数学试卷2．答卷前，考生必须将自己的学校、班级、姓名、试室、考号按要求填写在试卷密封线左边的空格内．答卷过程中考生不能使用计算器．一、选择题(本大题共10小题，每小题3分，共30分)在每小题给出的四个选项中，只有一个A ．±2B ．2C ．2D ．±22．点P （3，4）在（ ） A ． 第一象限B ．第二象限C ．第三象限D ．第四象限3．如图，直线a ∥b ，∠1=52°，则∠2的度数是（ ） A ． 38°B ． 52°C ． 128°D ．48°4．右图1通过平移后可以得到的图案是（ ）5．下列运算正确的是（ ） A ．=±3B ． |－3|=－3C ． －=－3D ． －32 = 96．在0，3.14159，3 ，227，39中，无理数的个数是（ ）A ． 1个B ． 2个C ． 3个D ． 4个7．点A 的坐标为（﹣2，﹣3），现将点A 向下平移2个单位，则经过平移后的对应点A′的坐标是（ ） A ．（﹣2，﹣1）B ．（﹣2，﹣5）C ．（0，﹣3）D ．（﹣4，﹣3）8．点到直线的距离是指（ ） A ．从直线外一点到这条直线的垂线 B ．从直线外一点到这条直线的垂线段 C ．从直线外一点到这条直线的垂线的长 D ．从直线外一点到这条直线的垂线段的长9．有下列四个命题：（1）相等的角是对顶角；（2）两条直线被第三条直线所截，同位角相等；（3）如果两条直线都和第三条直线平行，那么这两条直线也互相平行；（4）垂直于同一条直线的两条直线互相垂直。

其中是假命题．．．的有（ ） A ．1个 B ．2个 C ． 3个 D ．4个 10．如图2，直线a ∥b ，则|x ﹣y |=（ ） A ． 20 B ． 80 C ． 120D ． 180二、填空题(本大题共6小题，每小题4分，共24分)请将下列各题的正确答案填写在相应位置上。

高淳区2013～2014学年度第二学期期中质量调研检测七年级数学试卷一、选择题（每题2分，共16分. 请把正确答案的字母代号填在下面的表格中）1．某流感病毒的直径大约是000000081.0米，用科学记数法可表示为（▲） A .9101.8-⨯米 B .8101.8-⨯米 C .91081-⨯米 D .71081.0-⨯米 2．下列运算正确的是（▲）A . 623aa a =⋅B .222)(b a b a +=+C . 428aa a =÷D .22))((b a b a b a -=-+3．已知三角形的两边长分别为4和9，则此三角形的第三边长可以是（▲） A .4 B .5 C .9 D .13 4．下列各式能用平方差公式计算的是（▲） A .)2)(2(a b b a -+ B .)121)(121(--+-x x C .)2)((b a b a -+ D .)12)(12(+--x x 5．如图，点E 在BC 的延长线上，下列条件中能判断CD AB //的是（▲）A .43∠=∠B .DCE D ∠=∠C .D B ∠=∠ D .21∠=∠6．下列各式从左到右的变形，是因式分解的为（▲） A .623ab a b =⋅ B .()()103252-+=-+x x x x12 34EDC BA(第5题)C .()224168-=+-x x x D .x x x x x 6)3)(3(692+-+=+-7．如图，将三角尺的直角顶点放在直尺的一边上， 301=∠, 203=∠,则2∠的度数 等于（▲）A .50 B .30 C . 20D . 158．如图，两个正方形的边长分别为a 和b ，如果10=+b a ,20=ab ，那么阴影部分的 面积是（▲）A .10B .20C .30D .40二、填空题（每题2分，共20分）9．多项式mab ma 632-的公因式是 .10．如果一个多边形的内角和是1440，那么这个多边形的边数是 . 11．计算1112(0.25)(4)-⨯-= .12．若3,2-=-=+b a b a ，则=-22b a .13．已知等腰三角形的周长为17，一边长为4，则它的另两边长为 . 14．已知⎩⎨⎧==n,2y x 是方程组 ⎩⎨⎧=-=+122,2y x m y x 的解，则=m ，n = ．15．如图，将边长为cm 4的等边△ABC 沿边BC 向右平移cm 2得到△DEF ，则四边形ABFD 的周长为 .16．如图，将一个长方形纸条折成如图的形状，若已知1301=∠，则=∠2 °.17．若032=-+y x ，则yx42⋅的值为__________．18. 如图，△ABC 中,点E 是BC 上的一点，BE EC 2=，点D 是AC 的中点.123 (第7题)F b(第8题)(第15题)EDC BAF(第16题)12若△ABC 的面积12=∆ABC S ,则=-∆∆BEF ADF S S . 三、解答题（本题共8个小题，共64分）19.计算:(本题13分)(1)(3分) .21(3212---+-(2)(3分) .)3()()2(23a a a ⋅---(3) (3分)).2(4)32(2b a a b a ---(4) (4分))32)(32(-++-n m n m .20. 分解因式:(本题11分)(第18题)EDCBAF(1) (3分)a a a 36323+-.(2)(4分))()(22x y b y x a -+-.(3)(4分)22)(9)(16b a b a --+.21. (5分)先化简，再求值：2)2()2)(12(x x x ---+, 其中2-=x .22. (5分)解方程组 ⎩⎨⎧=+=-.42,132y x y x23.（6分）如图，在ABC ∆中， 40=∠B ，110=∠C .（1）画出下列图形：①BC 边上的高AD ；②A ∠的角平分线AE . （2）试求DAE ∠的度数.24.(6分)某停车场的收费标准如下：中型汽车的停车费为6元/辆，小型汽车的停车费为4元/辆.现在停车场共有36辆中、小型汽车，这些车共缴纳停车费176元.问中、小型汽车各有多少辆？(第23题)ACB①②25.(7分)如图，四边形ABCD 中，90=∠=∠C A ，BE 平分ABC ∠交CD 于E ，DF 平分ADC ∠交AB 于F .（1）若60=∠ABC ,则=∠ADC °,∠AFD （2）BE 与DF 平行吗？试说明理由.ED（第25题）E D1P图(2)CBA 2αP图(1)CBA 12αE D26.（11分）在等边ABC ∆中，点D 、E 分别是边AC 、AB 上的点(不与A 、B 、C 重合)，点P 是平面内一动点。

2013学年第二学期第二次教学质量分析(考试时间120分钟，满分120分)一 、 选择题(每题3分，共36分)1、下列所示的四个图形中，1∠和2∠是同位角．．．的是（ ）A 、 ② ③B 、 ① ② ③C 、 ① ② ④D 、 ① ④2、下列各方程：①4x-9=7-3x ；②2x +7y =15；③xy-y=1；④2x+3y=17．其中是二元一次方程的个数有几个（ ）A 、0B 、1C 、2D 、33、下列运算正确的是（ ）A 、 954a a a =+B 、33333a a a a =⋅⋅C 、954632a a a =⨯ D 、()743a a =-4、如图，能判断直线AB ∥CD 的条件是（ ）A 、∠1=∠2B 、∠3=∠4C 、∠1+∠3=180 oD 、∠3+∠4=180 o5、在二元一次方程x+3y=1的解中，当x=2时，对应的y 的值是（ ）A 、31B 、31-C 、1D 、46、用科学记数方法表示0000907.0，得……………………………………………（ ）A 、错误！未找到引用源。

B 、错误！未找到引用源。

C 、错误！未找到引用源。

D 、错误！未找到引用源。

7、为了保护生态环境，某县将一部分耕地改为林地。

改变后，林地的面积和耕地面积共有180平方千米，耕地面积是林地面积的25%，为求改变后林地面积和耕地面积各为多少平方千米，设耕地面积为x 平方千米，林地面积为y 平方千米，根据题意，列出如下四个方程组，其中正确的是（ ）A 、⎩⎨⎧==+x y y x %25180B 、⎩⎨⎧==+y x y x %25180C 、⎩⎨⎧=-=+%25180y x y x D 、⎩⎨⎧=-=+%25180x y y x8、计算（a －b ）（a+b ）（a 2+b 2）（a 4－b 4）的结果是（ ）A 、a 8+2a 4b 4+b 8B 、a 8－2a 4b 4+b 8C 、a 8+b 8D 、a 8－b 89、 如图，AB ∥CD ，且∠BAP=60°－α，∠APC=45°+α，∠PCD=30°－α，则α=( )A 、10°B 、15°C 、20°D 、30°10、如图，用8块相同的长方形地砖拼成一个宽为40cm 矩形，那么每块小长方形地砖的面积为( )A 、200cm 2B 、300cm 2C 、600cm 2D 、2400cm 211、已知X 2-5X-1=0，则代数式2X 2-5X+X -2的值是 ( )A 、22B 、24C 、26D 、2812、已知12216++n是一个有理数的平方，则n 不能取以下各数中的哪一个（ ）A 、30B 、 32C 、－18D 、9二 、填空题 （每题3分，共18分）13、如图，安装某管道，需经过两次拐弯，若要求拐弯后的管道与拐弯前的管道平行，第一次拐弯处的∠B ＝142°，那么第二次拐弯处的∠C ＝ 。

2013—2014学年度第二学期 七年级数学期中测试卷一、选择题（每小题2分，共20分）1、三条直线相交于1点，形成小于平角的对顶角共有( ) A 、3对 B 、4对 C 、5对 D 、6对2、如图所示，下列说法错误的是（ ）A 、∠1和∠3是同位角B 、∠1和∠2是同旁内角C 、∠1和∠4是内错角D 、∠4和∠5是同旁内角3、如图所示，DE 是过点A 的直线，下列条件中能判定DE ∥BC 的是（ ） A 、∠ACB=∠BAD B 、∠ACB=∠BAC C 、∠ACB=∠CAE D 、∠ACB=∠ABC24531D EBCA第1题图 第2题图 第3题图 4、在同一平面内，下列说法正确的是（ ）A 、不相交的两线段平行B 、不相交的两射线平行C 、线段与直线不平行就相交D 、不相交的两直线平行 5、下列命题中真命题的是（ ） A 、同位角相等 B 、同旁内角互补C 、同旁内角相等，两直线平行D 、平行于同一直线的两直线平行 6、下列说法中，正确的是（ ）A、任何数的平方根都有两个B、只有正数才有平方根C、不是正数，没有平方根D、正数的平方根的平方就是这个数7、的平方根是（）A、B、C 、D、8、若，则a与b的关系是（）A、a<bB、a>bC、a与b互为相反数D、2a=b9、若点P（x，y）在第四象限，|x|=3，|y|=2，则点P的坐标为（）A、（3，2）B、（-3，-2）C、（-3，2）D、（3，-2）10、若点M在（x，y）在第二象限，则点B（-x，-y）在（）A、第一象限B、第二象限C、第三象限D、第四象限二、填空题（每小题3分，共15分）11、把“对顶角相等”改写成“如果……那么……”的形式。

如果那么。

12、如图所示，已知两条直线a、b相交于点O，且∠1：∠2=1：2，则∠3= 度。

13、（—4）²是，16的算术平方根是。

14、若=5，则x= 。

15、点M（m+1，m+3）在x轴上，则点M的坐标为。

江苏省2013版13—14学年第二学期初一数学期终考试模拟三（时间：90分钟 满分：100分）班级_______ 姓名_______ 得分_______一、选择题（每小题2分，共20分）1．（2013．德阳）已知空气的单位体积质量为1.24×10－3克／厘米3，将 1.24×10－3用小数表示为( )A ．0.000124 B ．0.0124 C ．－0.00124 D ．0.001242．（2013．温州）下列各组数可能是一个三角形的边长的是 ( )A ．1，2，4B ．4，5，9C ．4，6，8D ．5，5，113．（2010．茂名）下列命题是假命题的是 ( )A ．三角形的内角和是180°B ．多边形的外角和都等于360°C ．五边形的内角和是900°D ．三角形的一个外角等于和它不相邻的两个内角的和4．（2013．广州）在6×6方格中，将图①中的图形Ⅳ平移后位置如图②所示，则图形N 的平移方法中，正确的是 ()题4题5题10A ．向下移动1格B ．向上移动1格C ．向上移动2格D ．向下移动2格5．（2013．永州）如图，下列条件中能判断直线l 1//l 2的是 ( )A ．∠1＝∠2B ．∠1＝∠5C ．∠1＋∠3＝180°D ．∠3＝∠56．（2013．锦州）下列运算正确的是 ( )A ．(a ＋b)2＝a 2＋b 2B ．x 3＋x 3＝x 6C ．(a 3)2＝a 5D ．（2x 2）（－3x 3)＝－6x 57．（2013．佛山）分解因式a 3－a 的结果是 ( )A ．a （a 2－1）B ．a(a －1)2C ．a （a ＋1）（a －1）D ．(a 2＋a)（a －1）8．（2013．郴州）在一年一度的“安仁春分药王节”市场上，小明的妈妈用280元买了甲、乙两种药材，甲种药材每斤20元，乙种药材每斤60元，且甲种药材比乙种药材多买了2斤，设买了甲种药材x 斤，乙种药材y 斤，你认为小明应该列出的方程组为 ( )A ．20602802x y x y +=⎧⎨-=⎩B ．60202802x y x y +=⎧⎨-=⎩C ．20602802x y y x +=⎧⎨-=⎩D ．60202802x y y x +=⎧⎨-=⎩9．（2013．南充）不等式组()3112323x x x ⎧+>-⎪⎨-+≥⎪⎩的整数解是 ( )A ．－1，0，1B ．0，1C ．－2，0，1D ．－1，110．（2013．内江）把一块直尺与一块三角板如图放置．若∠1＝40°，则∠2的度数为( )A ．125°B ．120°C ．140°D ．130°二、填空题（每小题3分，共18分）11．（2013．义乌）计算：3a ·a 2＋a 3＝_______．12．（2013．无锡）六边形的外角和等于_______．13．不等式（a －3）x>1的解集是x<1，则a 的取值范围_______．14．在△ABC 中，∠A ＝60°，∠B ＝2∠C ，则∠B ＝_______°．15．（2013．株洲）把多项式x 2＋mx ＋5因式分解得(x ＋5)（x ＋n ），则m ＝_______，n ＝_______．16．（2013．绥化）某班组织20名同学去春游，同时租用两种型号的车辆，一种车每辆有8个座位，另一种车每辆有4个座位，要求租用的车辆不留空座，也不能超载，有_______种租车方案．三、解答题（共62分）17．（12分）计算：(1)（－2ab 2）2·（3a 2b －2ab －1）； (2)22122a b ⎛⎫- ⎪⎝⎭；(3)(1＋x －y)(x ＋y －1)； (4)4（a －b)2－（2a ＋b ）(－b ＋2a)．18．（6分）（2013．荆州）用代入消元法解方程组23514x y x y -=⎧⎨+=⎩19．（9分）分解因式：(1)(a －3)2＋(3－a)； (2)a n ＋2＋a n ＋1－3a n ； (3)(a 2＋4)2－16a 2．20．（6分）（2013．镇江）解不等式组：()321931x x x -≥⎧⎪⎨+<+⎪⎩21．（8分）（2013．雅安）甲、乙二人在一环形场地上从A 点同时同向匀速跑步，甲的速度是乙的2.5倍，4分钟两人首次相遇，此时乙还需要跑300米才跑完第一圈，求甲、乙二人的速度及环形场地的周长．（列方程（组）求解）① ②① ②22．（8分）如图，∠AED＝∠ACB，∠DEB＝∠GFC，BE⊥AC，求证：FG⊥AC．23．（10分）（2012．哈尔滨）同庆中学为丰富学生的校园生活，准备从军跃体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格也相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．(1)购买一个足球、一个篮球各需多少元？(2)根据同庆中学的实际情况，需从军跃体育用品商店一次性购买足球和篮球共96个．要求购买足球和篮球的总费用不超过5 720元，则同庆中学最多可以购买多少个篮球？24．（10分）平面内的两条直线有相交和平行两种位置关系．(1)AB平行于CD，如图①，点P在AB、CD外部时，由AB∥CD，有∠B＝∠BOD，又∠BOD是△POD的外角，故∠BOD＝∠BPD＋∠D，得∠BPD＝∠B－∠D．如图②，将点P移到AB、CD内部，以上结论是否成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；(2)在图②中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图③，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）(3)根据(2)的结论求图④中∠4＋∠B＋∠C＋∠D＋∠E＋∠F的度数．参考答案1.D2.C3.C4.D5.C6.D7.C8.A9.A 10.D11．4a312．360°13．a<3 14．80 15．6 1 1 6．217．(1)原式＝12a4b5－8a3b5－4a2b4．(2)原式＝5b2－8ab．(3)原式＝x2－y2＋2y－1．(4)原式＝4a2－2ab2＋14b4．18．31 xy=⎧⎨=⎩19．(1)原式＝（a－3）（a－4）．(2)原式＝a n（a2＋a－3）．(3)原式＝(a－2)2(a＋2)2．20．x>321．375米／分、150米／分，环形场地周长为900米．22．略23．(1)50元，80元．(2)30个24．(1)不成立，结论是∠BPD＝∠B＋∠D．(2)结论：∠BPD＝∠BQD＋∠B＋∠D．(3)360°．。

2013～2014学年度第二学期第一次单元练习七 年 级 数 学(考试时间：100分钟 总分：100分 )一、选择题：（本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在．．答题纸相应位置．．．．．．．上．） 1．点P (3，-5)在 A ．第一象限内 B ．第二象限内 C ．第三象限内 D ．第四象限内 2． 若点M （a —2，2a ＋3）是x 轴上的点，则a 的值是A ．2B ．23 C ．32- D ．-23．实数5，－37，38-，3.1415，2π，0，4.1010010001中，无理数的个数为A ．2个B ．3个C ．4个D ．5个 4．设a ＝15－1，a 在两个相邻整数之间，则这两个整数是 A ．1和2 B ．2和3 C ．3和4 D ．4和55．如图，︒=∠+∠18021，︒=∠1053，则4∠度数为A ．︒75B ．︒85C ．︒95D ．︒105 6．如图，小明在操场上从A 点出发，先沿南偏东32°方向走到B 点， 再沿南偏东62°方向走到C 点．这时，∠ABC 的度数是A ．120°B ．135°C ．150°D ．160°7．在如图所示的数轴上，AB AC 2=，A 、B 两点对应的实数分别为5和—1，则点C 所对应的实数是A ．521+B ．531+C ．253+D ．252-8．下列命题中是真命题的是A ．从直线外一点到这条直线的垂线段叫做这点到这条直线的距离。

B ．过一点有且只有一条直线与已知直线平行C ．相等的角是对顶角D ．过一点有且只有一条直线与已知直线垂直9.将一个直角三角板和一把直尺如图放置，如果∠α=42 °， 则∠β余角的度数是 A ．︒42B ．︒48C ．︒30D ．︒6010. 如图，长方形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙分别由点A （2，0）同时出发，沿长方形BCDE 的边作环绕运动，物体甲按逆时针方向以2个单位/秒匀速运动，物体乙按顺时针方向以1个单位/秒匀速运动，则两个物体运动后的第2014次相遇地点的坐标是 A ．（2，0） B ．（1-，1） C ．（2-，1） D ．（1-，1-） 二、填空题：（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在．．．答题纸相应位置．．．．．．．上．） 11．5的平方根是 ▲ ． 12． 如果一个数的平方根等于这个数的立方根，那么这个数是 ▲ . 13．若8)1(3-=-x ，则=x ▲ .14．把一张长方形纸条按右图中那样折叠后，若得到∠AOB ′= 70º，则∠OGC = ▲ ．15．若414.12=，1414.0=a ，则a =_____▲___． 16．若点P （x ，y ）是第二象限内的点，点P 到x 轴距离为3，到y 轴距离为5，则点P 的坐标是 ▲ ．17．已知点A 坐标为）（52,2，若点A 是由点B 先向下平移5个单位，再向右平移2个单位得到的，则点B 的坐标为____▲_____.18．已知AB ∥ y 轴，A 点的坐标为（3，2），并且AB ＝5，则B 的坐标为 ▲ .三、解答题：（本大题共7小题，共56分．请在．．答题纸指定区域．．．．．．．内作答．．．，解答时应写出文 ac db4321'B 'C 1-05B C字说明、证明过程或演算步骤．）19（本题满分8分）计算（1）（4分）3201423125.01)2(274⨯---+-+）（（2）（4分）233333--+）（20. （本题满分7分）如图，请你从①C B ∠=∠，②AD 平分BAC ∠的邻补角CAE ∠，③AD ∥BC 这三个论断中选择两个作为已知条件，证明余下的一个成立。

2013-2014学年第二学期期中联考七年级数学试卷温馨提示：1．本试卷分试题卷和答题卷两部分。

满分100分，时间90分钟。

2．答题前，须在答题卷的密封区内填写学校、班级、姓名和考号。

3．所有答案都必须做在答题卷标定的位置上，注意试题序号和答题序号相对应。

一、选择题（本题有10小题，每小题3分，共30分）1．将如图所示的图案通过平移后可以得到的图案是（▲）2．下列方程中，属于二元一次方程的是（▲）A．2x+3=x－5 B．xy+y=2 C．3x﹣1=2﹣5y D．732=+yx3．计算：a4·a4 =（▲）`A．0a B．8aC．16a D．2a44．如图，属于同位角是（▲）A．∠1和∠2B．∠1和∠3C．∠1和∠4D．∠2和∠35．已知一个二元一次方程的一个解是11xy=⎧⎨=-⎩，则这个方程可能是（▲）A．3x y+=B．0x y+=C．3x y-=D．2x y=6．下列计算正确的是( ▲)A．3a+2a=5a2B．a3·2a2=2a6C．a4÷a2=a3D．(－3a3)2=9a6 7．人一根头发的直径大约为0.00072分米，用科学记数法表示正确的是（▲）A．57.210-⨯B．47.210-⨯C．57.210-⨯D．47.210-⨯8．下列整式乘法运算中，正确的是（▲）A．(x－y)(y+ x)=x2－y2B．（a+3）2=a2+9（第4题图）A. B. C. D.C ．(a +b )(－a －b )=a 2－b 2D ．(x －y )2=x 2－y 29．下列图形中，能由∠1=∠2得到AB //CD 的是（ ▲ ）10．若∠α与∠β的两边分别平行，且∠α =（x +10）°，∠β =（2x －25）°，则∠α的度数为（ ▲ ）A ．45°B ．75°C ．45°或75°D ．45°或55° 二、填空题：（本题有10小题，每小题3分，共30分）11．计算：1032()5-+= ▲ ．12．如图，若l 1∥l 2，∠1=50°，则∠2＝ ▲ °． 13．已知2x +y =2，用关于x 的代数式表示y ，则y = ▲ ． 14．如图，一张长为12cm ，宽为6cm 的长方形白纸中阴影 部分的面积（阴影部分间距均匀）是 ▲ cm 2．15．用加减法．．．解二元一次方程组23622x y x y +=⎧⎨-=⎩时，可将方程组变形为 ▲ . 16．若x +2y =1, 则2－x －2y = ▲ ．17．请你写出一个二元一次方程组．．．．．．．： ▲ ，使它的解为23x y =⎧⎨=⎩.18．如图，已知AD ∥BE ，∠DAC =29°，∠EBC =45°， 则∠ACB = ▲ °．19．已知8x ＝2，8y ＝5，则83x +2y20．现有一张边长为a 的大正方形卡片和三张边长为b 的小正方形卡片（12a b a <<）如图1，取出两张小卡片放入大卡片内拼成的图案如图2，再重新用三张小正方形卡片放入大卡片内拼成的图案如图3．已知图3中的阴影部分的面积比图2中的阴影部分的面积大2ab －6，则小正方形卡片的面积是 ▲ .A ．B．C．D ．（第14题图）（第18题图）（第12题图）（第20题图1）（图2）（图3）三、简答题（本题有6小题，共40分）解答应写出文字说明、推理过程或推演步骤。

2013—2014学年度下学期期末考试初一数学试题3（青岛版）一．选择题（共20小题）1．（2008•资阳）如图，CA⊥BE于A，AD⊥BF于D，下列说法正确的是（）2．（2004•青海）如图所示，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是（）3．（2013•本溪）如图，直线AB∥CD，直线EF与AB，CD分别交于点E，F，EC⊥EF，垂足为E，若∠1=60°，则∠2的度数为（）4．（2012•宜昌）如图，将三角尺与直尺贴在一起，使三角尺的直角顶点C（∠ACB=90°）在直尺的一边上，若∠1= 60°，则∠2的度数等于（）5．（2013•厦门）在平面直角坐标系中，将线段OA向左平移2个单位，平移后，点O、A的对应点分别为点O1、7．（2010•台湾）甲、乙两种机器分别以固定速率生产一批货物，若4台甲机器和2台乙机器同时运转3小时的总产量，与2台甲机器和5台乙机器同时运转2小时的总产量相同，则1台甲机器运转1小时的产量，与1台乙机器．C D8．（2009•东营）关于x，y的二元一次方程组的解也是二元一次方程2x+3y=﹣6的解，则k的值是（）C D3211．（2011•台湾）如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角．关于这七个角的度数关系，下列何者正确（）12．（2010•长春）如图，△ABC中，∠C=90°，∠B=40°．AD是角平分线，则∠ADC的度数为（）15．有两个圆，⊙O1的半径等于地球的半径，⊙O2的半径等于一个篮球的半径，现将两个圆都向外膨胀（相当于作同心圆），使周长都增加1米，则半径伸长的较多的圆是（）432222二．填空题（共5小题）21．（2009•芜湖）计算：33°52′+21°54′=_________度_________分．22．（2013•玉林）如图，在直角坐标系中，O是原点，已知A（4，3），P是坐标轴上的一点，若以O，A，P三点组成的三角形为等腰三角形，则满足条件的点P共有_________个，写出其中一个点P的坐标是_________．23．（2013•永州）钓鱼岛列岛是我国固有领土，共由8个岛屿组成，其中最大的岛是钓鱼岛，面积约为4.3平方公里，最小的岛是飞濑屿，面积约为0.0008平方公里．请用科学记数法表示飞濑屿的面积约为_________平方公里．24．两同心圆的圆心为O，大圆半径为3，小圆半径为1，大圆的直径与小圆相交于B、C两点，分别以B、C为圆心、以2为半径作半圆（如图所示），则阴影部分面积为_________平方单位．25．（2013•乐山）如图，在四边形ABCD中，∠A=45°．直线l与边AB，AD分别相交于点M，N，则∠1+∠2=_________．三．解答题（共4小题）26．（2012•宿迁）求代数式（a+2b）（a﹣2b）+（a+2b）2﹣4ab的值，其中a=1，b=．27．（2013•聊城）夏季来临，天气逐渐炎热起来，某商店将某种碳酸饮料每瓶的价格上调了10%，将某种果汁饮料每瓶的价格下调了5%，已知调价前买这两种饮料各一瓶共花费7元，调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元，问这两种饮料在调价前每瓶各多少元？28．在等边△ABC中，点D、E分别是边AC、AB上的点（不与A、B、C重合），点P是平面内一动点．设∠PDC=∠1，∠PEB=∠2，∠DPE=∠a．（1）若点P在边BC上运动（不与点B和点C重合），如图（1）所示．则∠1+∠2=_________．（用α的代数式表示）（2）若点P在△ABC的外部，如图（2）所示．则∠α、∠1、∠2之间有何关系？写出你的结论，并说明理由．（3）当点P在边BC的延长线上运动时，试画出相应图形，并写出∠α、∠1、∠2之间的关系式．（不需要证明）29．在直角坐标平面内，已知点A（0，5）和点B（﹣2，﹣4），BC=4，且BC∥x轴．（1）在图中画点C的位置，并写出点C的坐标；（2）连接AB、AC、BC，判断△ABC的形状，并求出它的面积．2013—2014学年度下学期期末考试初一数学试题（青岛版）参考答案与试题解析一．选择题（共20小题）1．（2008•资阳）如图，CA⊥BE于A，AD⊥BF于D，下列说法正确的是（）2．（2004•青海）如图所示，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是（）3．（2013•本溪）如图，直线AB∥CD，直线EF与AB，CD分别交于点E，F，EC⊥EF，垂足为E，若∠1=60°，则∠2的度数为（）4．（2012•宜昌）如图，将三角尺与直尺贴在一起，使三角尺的直角顶点C（∠ACB=90°）在直尺的一边上，若∠1= 60°，则∠2的度数等于（）5．（2013•厦门）在平面直角坐标系中，将线段OA向左平移2个单位，平移后，点O、A的对应点分别为点O1、7．（2010•台湾）甲、乙两种机器分别以固定速率生产一批货物，若4台甲机器和2台乙机器同时运转3小时的总产量，与2台甲机器和5台乙机器同时运转2小时的总产量相同，则1台甲机器运转1小时的产量，与1台乙机器．C D小时的产量相同，8．（2009•东营）关于x，y的二元一次方程组的解也是二元一次方程2x+3y=﹣6的解，则k的值是（）C D得：﹣3211．（2011•台湾）如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角．关于这七个角的度数关系，下列何者正确（）12．（2010•长春）如图，△ABC中，∠C=90°，∠B=40°．AD是角平分线，则∠ADC的度数为（）∠15．有两个圆，⊙O1的半径等于地球的半径，⊙O2的半径等于一个篮球的半径，现将两个圆都向外膨胀（相当于作，=r+；R=r=，432220．（2007•云南）已知x+y=﹣5，xy=6，则x2+y2的值是（）二．填空题（共5小题）21．（2009•芜湖）计算：33°52′+21°54′=55度46分．22．（2013•玉林）如图，在直角坐标系中，O是原点，已知A（4，3），P是坐标轴上的一点，若以O，A，P三点组成的三角形为等腰三角形，则满足条件的点P共有8个，写出其中一个点P的坐标是（5，0）．，（23．（2013•永州）钓鱼岛列岛是我国固有领土，共由8个岛屿组成，其中最大的岛是钓鱼岛，面积约为4.3平方公里，最小的岛是飞濑屿，面积约为0.0008平方公里．请用科学记数法表示飞濑屿的面积约为8×10﹣4平方公里．24．两同心圆的圆心为O，大圆半径为3，小圆半径为1，大圆的直径与小圆相交于B、C两点，分别以B、C为圆心、以2为半径作半圆（如图所示），则阴影部分面积为4π平方单位．∴SS﹣25．（2013•乐山）如图，在四边形ABCD中，∠A=45°．直线l与边AB，AD分别相交于点M，N，则∠1+∠2=225°．三．解答题（共4小题）26．（2012•宿迁）求代数式（a+2b）（a﹣2b）+（a+2b）2﹣4ab的值，其中a=1，b=．b=27．（2013•聊城）夏季来临，天气逐渐炎热起来，某商店将某种碳酸饮料每瓶的价格上调了10%，将某种果汁饮料每瓶的价格下调了5%，已知调价前买这两种饮料各一瓶共花费7元，调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元，问这两种饮料在调价前每瓶各多少元？．28．在等边△ABC中，点D、E分别是边AC、AB上的点（不与A、B、C重合），点P是平面内一动点．设∠PDC=∠1，∠PEB=∠2，∠DPE=∠a．（1）若点P在边BC上运动（不与点B和点C重合），如图（1）所示．则∠1+∠2=60°+α．（用α的代数式表示）（2）若点P在△ABC的外部，如图（2）所示．则∠α、∠1、∠2之间有何关系？写出你的结论，并说明理由．（3）当点P在边BC的延长线上运动时，试画出相应图形，并写出∠α、∠1、∠2之间的关系式．（不需要证明）29．在直角坐标平面内，已知点A（0，5）和点B（﹣2，﹣4），BC=4，且BC∥x轴．（1）在图中画点C的位置，并写出点C的坐标；（2）连接AB、AC、BC，判断△ABC的形状，并求出它的面积．BC9=×==×。

2013-2014学年度下学期期末考试数学试题一．选择题（共20小题）13． CD ．5．（2009•济南）在平面直角坐标系中，对于平面内任一点（a ，b ），若规定以下三种变换：1、f （a ，b ）=（﹣a ，b ）．如：f （1，3）=（﹣1，3）；2、g （a ，b ）=（b ，a ）．如：g （1，3）=（3，1）；3、h （a ，b ）=（﹣a ，﹣b ）．如：h （1，3）=（﹣1，﹣3）．7．（2012•临沂）关于x 、y 的方程组的解是，则|m ﹣n|的值是（ ）9．（2013•遵义）计算（﹣ab 2）3的结果是（ ）a a15．（2006•安徽）如图是由10把相同的折扇组成的“蝶恋花”（图1）和梅花图案（图2）（图中的折扇无重叠），则梅花图案中的五角星的五个锐角均为（）1317．（2011•长春）如图，直线l1∥l2，点A在直线l1上，以点A为圆心，适当长为半径画弧，分别交直线l1、l2于B、18．（2007•南平）如图，甲顺着大半圆从A地到B地，乙顺着两个小半圆从A地到B地，设甲、乙走过的路程分别为a、b，则（）18 17 2219．（2006•厦门）在平面直角坐标系内存在⊙A，A（b，0），⊙A交x轴于O（0，0）、B（2b，0），在y轴上存在一动点C（C不与原点O重合），直线l始终过A、C，直线l交⊙A于E、F，在半圆EF上存在一点动点D且D不与．C D21．（2014•南充）分解因式：x3﹣6x2+9x=_________．22．（2006•双流县）如图，将一副三角板叠放在一起，使直角顶点重合于点O，如果∠AOD=130°，那么∠BOC=_________度．23．（2013•聊城）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为_________（用n表示）．24．（2002•常州）如果把人的头顶和脚底分别看作一个点，把地球赤道看作一个圆，那么身高2m的小赵沿着赤道环行一周，他的头顶比脚底多行_________m．25．（2012•广安）如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=_________度．三．解答题（共5小题）26．计算下列各小题．（1）4a﹣2b3•（﹣ab﹣2）3•（）﹣2•（2013）0；（2）（3×10﹣3）3÷（2×10﹣2）2．27．（2013•北京）已知x2﹣4x﹣1=0，求代数式（2x﹣3）2﹣（x+y）（x﹣y）﹣y2的值．28．（2009•漳州）给出三个多项式：x2+2x﹣1，x2+4x+1，x2﹣2x．请选择你最喜欢的两个多项式进行加法运算，并把结果因式分解．29．已知：△ABC中，AD⊥BC，AE平分∠BAC，请根据题中所给的条件，解答下列问题：（1）如图1，若∠BAD=60°，∠EAD=15°，求∠ACB的度数．（2）通过以上的计算你发现∠EAD和∠ACB﹣∠B之间的关系应为：_________．（3）在图2的△ABC中，∠ACB＞90°，那么（2）中的结论仍然成立吗？为什么？30．已知平面直角坐标系中，有四个点A（﹣3，0）、B（0，﹣4）、C（3，0）、D（0，4）（1）在下面的平面直角坐标系中描出各点，并顺次连接得到一个四边形；（2）求三角形ABC的面积．（3）若以A、B、C、E四点为顶点的四边形是平行四边形，请你直接写出点E的坐标．31、已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．根据以上信息，解答下列问题：（1）1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？（2）请你帮该物流公司设计租车方案；（3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．2014年06月17日赵国英的初中数学组卷参考答案与试题解析一．选择题（共20小题）1．（2013•六盘水）直尺与三角尺按如图所示的方式叠放在一起，在图中所标记的角中，与∠1互余的角有几个（）3．（2013•昭通）如图，AB∥CD，DB⊥BC，∠2=50°，则∠1的度数是（）．C D ．5．（2009•济南）在平面直角坐标系中，对于平面内任一点（a ，b ），若规定以下三种变换：1、f （a ，b ）=（﹣a ，b ）．如：f （1，3）=（﹣1，3）；2、g （a ，b ）=（b ，a ）．如：g （1，3）=（3，1）；3、h （a ，b ）=（﹣a ，﹣b ）．如：h （1，3）=（﹣1，﹣3）．，＞7．（2012•临沂）关于x、y的方程组的解是，则|m﹣n|的值是（）方程组的解是，∴，8．（2012•佳木斯）某校团委与社区联合举办“保护地球，人人有责”活动，选派20名学生分三组到120个店铺发传单，若第一、二、三小组每人分别负责8、6、5个店铺，且每组至少有两人，则学生分组方案有（）9．（2013•遵义）计算（﹣ab2）3的结果是（）a a（﹣（﹣）a213．（2013•湘西州）如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（）15．（2006•安徽）如图是由10把相同的折扇组成的“蝶恋花”（图1）和梅花图案（图2）（图中的折扇无重叠），则梅花图案中的五角星的五个锐角均为（）16．（2011•十堰）现有边长相同的正三角形、正方形和正六边形纸片若干张，下列拼法中不能镶嵌成一个平面图案n17．（2011•长春）如图，直线l1∥l2，点A在直线l1上，以点A为圆心，适当长为半径画弧，分别交直线l1、l2于B、C两点，连接AC、BC．若∠ABC=54°，则∠1的大小为（）18．（2007•南平）如图，甲顺着大半圆从A地到B地，乙顺着两个小半圆从A地到B地，设甲、乙走过的路程分别为a、b，则（），则两个小半圆的直径之和是大半圆的直径．19．（2006•厦门）在平面直角坐标系内存在⊙A，A（b，0），⊙A交x轴于O（0，0）、B（2b，0），在y轴上存在一动点C（C不与原点O重合），直线l始终过A、C，直线l交⊙A于E、F，在半圆EF上存在一点动点D且D不与．C D×的最大值为：．二．填空题（共5小题）21．（2014•南充）分解因式：x3﹣6x2+9x=x（x﹣3）2．22．（2006•双流县）如图，将一副三角板叠放在一起，使直角顶点重合于点O，如果∠AOD=130°，那么∠BOC=50度．23．（2013•聊城）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为（2n，1）（用n表示）．24．（2002•常州）如果把人的头顶和脚底分别看作一个点，把地球赤道看作一个圆，那么身高2m的小赵沿着赤道环行一周，他的头顶比脚底多行4πm．25．（2012•广安）如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=240度．三．解答题（共5小题）26．计算下列各小题．（1）4a﹣2b3•（﹣ab﹣2）3•（）﹣2•（2013）0；（2）（3×10﹣3）3÷（2×10﹣2）2．ab（（﹣27．（2013•北京）已知x2﹣4x﹣1=0，求代数式（2x﹣3）2﹣（x+y）（x﹣y）﹣y2的值．28．（2009•漳州）给出三个多项式：x2+2x﹣1，x2+4x+1，x2﹣2x．请选择你最喜欢的两个多项式进行加法运算，并把结果因式分解．x1+情况二：x情况三：+4x+1+x29．已知：△ABC中，AD⊥BC，AE平分∠BAC，请根据题中所给的条件，解答下列问题：（1）如图1，若∠BAD=60°，∠EAD=15°，求∠ACB的度数．（2）通过以上的计算你发现∠EAD和∠ACB﹣∠B之间的关系应为：∠ACB﹣∠B=2∠EAD．（3）在图2的△ABC中，∠ACB＞90°，那么（2）中的结论仍然成立吗？为什么？30．已知平面直角坐标系中，有四个点A（﹣3，0）、B（0，﹣4）、C（3，0）、D（0，4）（1）在下面的平面直角坐标系中描出各点，并顺次连接得到一个四边形；（2）求三角形ABC的面积．（3）若以A、B、C、E四点为顶点的四边形是平行四边形，请你直接写出点E的坐标．的面积为=12。

江阴市山观二中2013-2014学年度第二学期初一数学期末试卷 2014.6命题人：梅莉娜 审核人：吴晓刚一、精心选一选：（本大题共8小题，每题3分，共24分）1．下列运算正确的是 （ ） A 、2x+3y=5xy B 、5m 2·m 3=5m 5 C 、（a —b ）2=a 2—b 2 D 、m 2·m 3=m 6 2．已知实数a 、b ，若a >b ，则下列结论正确的是 （ ） A.55-<-b a B.b a +<+22 C.33ba < D.b a 33>对顶角；④同位角相等。

其中假命题有 （ ） A ．1个 B.2个 C.3个 D.4个5. 如果关于x 、y 的方程组⎩⎪⎨⎪⎧x －y =a ，3x ＋2y =4的解是正数，那么a 的取值范围是 （ ）A ．－2＜a ＜43B ．a ＞－43C ．a ＜2D ．a ＜－436. 下图能说明∠1>∠2的是 ( )7．某校去年有学生1 000名，今年比去年增加4.4%，其中住宿学生增加6%，走读生减少2%。

若设该校去年有住宿学生有x 名，走读学生有y 名，则根据题意可得方程组 ( ) A . 1000,6%2% 4.4%1000.x y x y +=⎧⎨-=⨯⎩B . 1000,106%102%1000(1 4.4%).x y x y +=⎧⎨-=+⎩C . 1000,6%2% 4.4%1000.x y x y +=⎧⎨+=⨯⎩D . 1000,106%102%1000(1 4.4%).x y x y +=⎧⎨+=+⎩8.如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第二、细心填一填：（本大题共10小题，每空2分，共22分） 9．拒绝“餐桌浪费”，刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克，这个数据用科学计数法表示为 吨。

10. 若方程组，则3（x+y ）﹣（3x ﹣5y ）的值是 ．11. 已知10m ＝3，10n ＝5，则103m －n ＝ ．12.计算)8)(4(22+++-mx x n x x 的结果不含2x 和3x 的项，那么m = ；n = . 13．命题“两直线平行，同旁内角相等”是 命题（填“真”或“假”）． 14.将一副学生用三角板按如图所示的方式放置．若AE ∥BC ，则∠AFD 的度数是 ．第14题图 第16题15．端午佳节，某商场进行促销活动，将定价为3元的水笔，以下列方式优惠销售：若购买不超过10支，按原价付款；若一次性购买10支以上打八折．如果用30元钱，最多可以购买该水笔的支数是_______．16.如图，四边形ABCD 中，点M ，N 分别在AB ，BC 上，将△BMN 沿MN 翻折，得△FMN ，若MF ∥AD ，FN ∥DC , 则∠B = °． 17．若不等式组的解集为3≤x≤4，则不等式ax+b ＜0的解集为 ．18.若方程组 2313,3530.9a b a b -=⎧⎨+=⎩ 的解是 8.3,1.2,a b =⎧⎨=⎩ 则方程组 2(2)3(1)13,3(2)5(1)30.9x y x y +--=⎧⎨++-=⎩的解是 ．三、认真答一答：（本大题共9小题，共54分. ）19．（4分）计算：)2)(2()1(2-+-+x x x 20．（4分）分解因式： 2x 4﹣221．（4分）解方程组．22．解不等式（组）（4分+4分） （1）解不等式：，并把解集表示在数轴上．（2）求不等式组的正整数解．23．（5分）定义：对于实数a ，符号[a ]表示不大于a 的最大整数．例如：[5.7]=5，[5]=5，[﹣π]=﹣4．（1）如果[a ]=﹣2，那么a 的取值范围是 ． （2）如果[]=3，求满足条件的所有正整数x ．24. (6分) 在△ABC 中，AE ⊥BC 于点E ，∠BAE :∠CAE ＝2:3，BD 平分∠ABC ，点F 在BC 上，∠CDF ＝30°，∠ABD ＝35°．求证：DF ⊥BC ．25．（6分）甲、乙二人在一环形场地上从A 点同时同向匀速跑步，甲的速度是乙的2.5倍，4分钟两人首次相遇，此时乙还需要跑300米才跑完第一圈，求甲、乙二人的速度及环形场地的周长．（列方程（ 组） 求解） 26．（8分）某校住校生宿舍有大小两种寝室若干间，据统计该校高一年级男生740人，使用了55间大寝室和50间小寝室，正好住满；女生730人，使用了大寝室50间和小寝室55间，也正好住满．（1）求该校的大小寝室每间各住多少人？ （2）预测该校今年招收的高一新生中有不少于630名女生将入住寝室80间，问该校有多少种安排住宿的方案？AB D F27.（9分）如图，四边形ABCD 中，AD ∥BC ，DE 平分∠ADB ，∠BDC=∠BCD ．（1）求证：∠1+∠2=90°；（2）若H 是BC 上一动点，F 是BA 延长线上一点，FH 交BD 于M ，FG 平分∠BFH ，交DE 于N ，交BC 于G ．当H 在BC 上运动时（不与B 点重合），的值是否变化？如果变化，说明理由；如果不变，试求出其值．江阴市要塞中学2013- 2014学年度第二学期初一数学期末考试答案二、填空题：(本大题共10小题，每小题2分，共22分)9．__ _5×107__ 10．___24___11．___ 5.4 __ 12．_ 4；8____13．_ 假 14．750_ 15． 12 16．__950____17. x 〉1.5 18. x=6.3,y=2.2 三、解答题（本大题共9小题，共54分．） 19．(本题满分4分) 解： （1）)2)(2()1(2-+-+x x x=x 2+2x+1-(x 2-4)-------------------------2分 = x 2+2x+1-x 2+4--------------------------3分=2x+5 ---------------------------------4分 20．(本题满分4分)解：(2) 原式=2（x 4﹣1）=2（x 2+1）（x 2﹣1）--------------------------------------------2分=2（x 2+1）（x+1）（x ﹣1）．------------------------------------4分21．(本题满分4分)解：，由①得，x=2y+4③，-------------------------------------------1分③代入②得2（2y+4）+y﹣3=0，解得y=﹣1，-------------------------------------------2分把y=﹣1代入③得，x=2×（﹣1）+4=2，------------------------------------------3分所以，方程组的解是．---------------------------------------------4分22．（1）(本题满分4分)解：去分母得：2（2x﹣1）﹣（9x+2）≤6，----------1分去括号得：4x﹣2﹣9x﹣2≤6，移项得：4x﹣9x≤6+2+2，合并同类项得：﹣5x≤10，把x的系数化为1得：x≥﹣2．------------3分----------------------------4分（2）(本题满分4分)解：解不等式2x+1＞0，得：x ＞﹣，----------------------1解不等式x＞2x﹣5得：x＜5，-------------------2分∴不等式组的解集为﹣＜x＜5，-------------------------3分∵x是正整数，∴x=1、2、3、4、5．--------------------------------------------------4分23．(本题满分5分)（1）﹣2≤a＜﹣1--------------------------------------------------------------2分（2）根据题意得：3≤[]＜4，-------------------------------------------------3分解得：5≤x＜7，------------------------------------------4分则满足条件的所有正整数为5，6．----------------------------------------5分24．（本题满分6分）证明:∵BD平分∠ABC，∠ABD=35°∴∠ABC=2∠ABD=70°………………………………………………（2分）∵AE⊥BC ∴∠AEB=90°∴∠BAE=20°…………………………（3分）又∵∠BAE：∠CAE=2：3 ∴∠CAE=30°………………………（4分）又∵CDF=30°∴∠CAE=∠CDF …………………………………（5分）∴DF∥AE ∴DF⊥BC……………………………………………（6分）C ABD F25．（本题满分6分）解：设乙的速度为x米/秒，则甲的速度为2.5x米/秒，环形场地的周长为y米，-----1分由题意，得，-----------------------------------------------------------------3分解得：，-------------------------------------------------------------------4分∴甲的速度为：2.5×150=375米/分．------------------------------------------------5分答：乙的速度为150米/分，则甲的速度为375米/分，环形场地的周长为900米．-----6分26．（本题满分8分）解：（1）设该校的大寝室每间住x人，小寝室每间住y人，------------------1分由题意得：，---------------------------------------3分解得：，----------------------------------4分答：该校的大寝室每间住8人，小寝室每间住6人；（2）设大寝室a间，则小寝室（80﹣a）间，由题意得：，------------------------------------------------------6分解得：80≥a≥75，①a=75时，80﹣75=5，②a=76时，80﹣a=4，③a=77时，80﹣a=3，④a=78时，80﹣a=2，⑤a=79时，80﹣a=1，⑥a=80时，80﹣a=0．故共有6种安排住宿的方案．-----------------------------------8分27. （本题满分9分）证明：（1）AD∥BC，∠ADC+∠BCD=180，----------------------------------------------1分∵DE平分∠ADB，∴∠ADE=∠EDB，----------------------------------2分∵∠ADC+∠BCD=180°，∠BDC=∠BCD，∴∠EDB+∠BDC=90°，--------------------------------------------3分∠1+∠2=90°．---------------------------------------------------------4分（2）---------------5分∴-----------------------------------------------------7分∵--------------------------------------------------------------9分本试卷学生预计得分：78分考点分布：(1)平面图形的认识：11分(2)幂的运算：7分(3)整式乘法与因式分解：14分(4)二元一次方程组：21分(5)一元一次不等式：28分(6)证明：19分。

2013—2014学年度七年级第二学期期末调研考试数 学 试 卷（人教版）注意：本试卷共8页，满分为120分，考试时间为120分钟．一、选择题（本大题共12个小题；每小题2分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．点到直线的距离是指……………………………………………………………（ ） A ．从直线外一点到这条直线的垂线 B ．从直线外一点到这条直线的垂线段 C ．从直线外一点到这条直线的垂线的长 D ．从直线外一点到这条直线的垂线段的长2．如图，将直线l 1沿着AB 的方向平移得到直线l 2，若∠1=50°， 则∠2的度数是…………………………………………（ ） A ．40° B ．50° C ．90° D ．130°3．下列语句中正确的是…………………………………………………………（ ） A ．-9的平方根是-3 B ．9的平方根是3 C ．9的算术平方根是±3 D ．9的算术平方根是34．下列关于数的说法正确的是……………………………………………………（ ） A ．有理数都是有限小数 B ．无限小数都是无理数 C ．无理数都是无限小数 D ．有限小数是无理数5．点（-5，1）所在的象限是……………………………………………………（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．将点A （2，1）向左平移2个单位长度得到点A ′，则点A ′的坐标是………（ ） A ．（0，1） B ．（2，－1） C ．（4，1） D ．（2，3）7．下列调查中，适宜采用全面调查方式的是……………………………………（ ） A ．对我国首架大陆民用飞机各零部件质量的检查A Bl 1l 212 (2题图)B ．调查我市冷饮市场雪糕质量情况C ．调查我国网民对某事件的看法D ．对我市中学生心理健康现状的调查8．二元一次方程3x ＋2y ＝11………………………………………………………（ ） A ．任何一对有理数都是它的解 B ．只有一个解 C ．只有两个解 D ．有无数个解9．方程组⎩⎨⎧=+=+32y x y x ■，的解为⎩⎨⎧==■y x 2，则被遮盖的两个数分别为…………（ ）A ．1，2B ．5，1C ．2，3D ．2，410．如图是甲、乙两户居民家庭全年支出费用的扇形统计图，根据统计图，下面对食品支出费用判断正确的是…………………………………………………………（ ）A ．甲户比乙户多B ．乙户比甲户多C ．甲、乙两户一样多D ．无法确定哪一户多11．如图，点O 在直线AB 上，OC 为射线，∠1比∠2的3倍少10°，设∠1，∠2的度数分别为x ，y ，那么下列求出这两个角的度数的方程是………………………（ ）A ．⎩⎨⎧-==+10180y x y xB ．⎩⎨⎧-==+103180y x y xC ．⎩⎨⎧+==+10180y x y x D ．⎩⎨⎧-==1031803y x y12．5名学生身高两两不同，把他们按从高到低排列，设前三名的平均身高为a 米，后两名的平均身高为b 米．又前两名的平均身高为c 米，后三名的平均身高为d 米，则………………………………………………………………………………（ ） A ．2b c +＞2b a + B ．2b a +＞2b c + C ．2b c +=2ba +D ．以上都不对ABC1 2O (11题图)二、填空题（本大题共8个小题；每小题3分，共24分．把答案写在题中横线上）13．在同一平面内，已知直线a 、b 、c ，且a ∥b ，b ⊥c ，那么直线a 和c 的位置关系是___________． 14．下列说法中①两点之间，直线最短；②经过直线外一点，能作一条直线与这条直线平行； ③和已知直线垂直的直线有且只有一条；④在平面内过一点有且只有一条直线垂直于已知直线． 正确的是：_______________．（只需填写序号）15．11在两个连续整数a 和b 之间，a ＜11＜b ，那么b a 的立方根是____________． 16．在实数3.14,－36.0,－66,0.13241324…,39 ,－π,32中，无理数的个数是______． 17．一只蚂蚁由（0，0）先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是_________．18．某空调生产厂家想了解一批空调的质量，把仓库中的空调编上号，然后抽取了编号为5的倍数的空调进行检验．你认为这种调查方式_____________．(填“合适”或“不合适”)19．如图，围棋盘放置在某个平面直角坐标系内，如果白棋②的坐标为(－7,－4)，白棋④的坐标为(－6,－8)，那么黑棋的坐标应该是_________________．20．如图，母亲节那天，很多同学给妈妈准备了鲜花和礼盒．从图中信息可知，则买5束鲜花和5个礼盒的总价为________元．(19题图)(20题图)三、解答题（共72分．解答应写出文字说明、证明过程或演算步骤） 21．解下列方程组或不等式（组）:（1，2小题各4分，3小题6分， 共14分）（1）⎩⎨⎧-=+=+;62,32y x y x（2）⎩⎨⎧=-=+;2463,247y x y x（3）解不等式组，并把它的解集表示在数轴上：3(1)7251.3x x xx --⎧⎪⎨--<⎪⎩≤， ① ②22．（本题8分）如图，CD 平分∠ACB ，DE ∥BC ，∠AED =80°，求∠EDC 的度数．23．（本题6分）小刘是快餐店的送货员，如果快餐店的位置记为（0,0），现有位置分别是A （100,0），B （150，－50），C （50, 100）三位顾客需要送快餐，小刘带着三位顾客需要的快餐从快餐店出发，依次送货上门服务，然后回到快餐店．请你设计一条合适的送货路线并计算总路程有多长．（画出坐标系后用“箭头”标出）ADB CE24．（本题10分）已知：如图，AD ⊥BC 于D ，EG ⊥BC 于G ，AE =AF ．求证：AD 平分∠BAC ．25．应用题(本题10分)某校为了解七年级学生体育测试情况，以七年级(1)班学生的体育测试成绩为样本，按A ，B ，C ，D 四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给的信息解答下列问题：（说明：A 级：90分～100分；B 级：75分～89分；C 级：60分～74分；D 级：60分以下）（1）请把条形统计图补充完整；（2）样本中D 级的学生人数占全班学生人数的百分比是__________； （3）扇形统计图中A 级所在的扇形的圆心角度数是__________；（4）若该校七年级有500名学生，请你用此样本估计体育测试中A 级和B 级的学生人数约为多少人．(24题图)FE ACBGD3 2 1C BD A 46% 20%24%如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．已知公路运价为1.5元/（吨·千米），铁路运价为1.2元/（吨·千米），且这两次运输共支出公路运输费15000元，铁路运输费97200元．求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？（2）这批产品的销售款比原料费与运输费的和多多少元？（1）如图，∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC，求∠MON 的度数．（2）如果（1）中∠AOB＝α，其他条件不变，求∠MON的度数．（3）如果（1）中∠BOC＝β（β为锐角），其他条件不变，求∠MON的度数．（4）从（1）（2）（3）的结果能看出什么规律？（5）线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法，请你模仿（1）～（4），设计一道以线段为背景的计算题，写出其中的规律来？AMBONC2-1-0 1参考答案题号 1 2 3 4 5 6 7 8 9 10 1112 答案DBDCBAADBDB A12∵a ＞d ，∴2a +2b ＜2c +2d ， ∴a +b ＜c +d ，∴＜， 即＞，故选B ．二、填空题 13．a ⊥c ； 14．②，④； 15．4； 16．3； 17．（3，2）；18．合适 点拨：因为这样使得该抽样调查具有随机性、代表性． 19．(－3,－7)； 20．440． 三、解答题： 21．（1）解：由①得：y =－2x +3……③ ③代入② x +2（－2x +3）=－6 x =4………………………………………………………………………………2分把x =4代入③得 y =－5 ∴原方程组解为 ⎩⎨⎧-==54y x ………………4分（2）解：①×3+②×2得： 27x =54x =2把x =2代入①得：4y =－12y =－3………………………………………………………………………2分 ∴原方程组解为 ⎩⎨⎧-==32y x ……………………………………………4分（3）解：解不等式①，得2x -≥； 解不等式②，得12x <-．在同一条数轴上表示不等式①②的解集，如图所示：…………………………2分……………………………………4分所以，原不等式组的解集是122x -<-≤．……………………………………6分 22．解：∵ DE ∥BC ，∠AED =80°，∴ ∠ACB =∠AED =80°. ………………………………………4分 ∵ CD 平分∠ACB ， ∴ ∠BCD =21∠ACB =40°，……………………………………6分 ∴ ∠EDC =∠BCD =40°．…………………………………………8分 23．解：合适的路线有四条，如图所示是其中的一条， 即向北走100 m ，再向东走50 m 到C ；接着向南走 100 m ，再向东走50 m 到A ；接着向东走50 m ，再向 南走50 m 到B ；接着向西走150 m ，再向北走50 m 回到O .尽可能少走重复路段．如图所示，所走的路线 长最短，共为600 m. …………………………………6分 24．证明：∵AD ⊥BC 于D ，EG ⊥BC 于G∴AD ∥EG ，………………………3分 ∴∠2=∠3, ∠1=∠E , ………………5分 ∵AE =AF ∴∠E = ∠3，∴∠1 = ∠2，……………………………8分 ∴AD 平分∠BAC ．………………………10分 25．解：(1)条形图补充如图所示．………………3分(2)10%……………………………………5分 (3)72°……………………………………7分 (4)500×(46%＋20%)＝330(人)．………………10分26．解：（1）设工厂从A 地购买了x 吨原料,制成运往B 地的产品y 吨.则依题意，得：⎩⎨⎧=+=+.97200)120110(2.1,15000)1020(5.1x y x y …………………………………6分DB七年级(下)数学期末试卷 第11页(共8页) 解这个方程组，得：⎩⎨⎧==.300,400y x ∴工厂从A 地购买了400吨原料,制成运往B 地的产品300吨. ……………………………………………………………9分（2）依题意，得：300×8000－400×1000－15000－97200=1887800∴批产品的销售款比原料费与运输费的和多1887800元. ……………………12分27．解：(1)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12×120°－12×30°＝45°； ……………………………………………………………2分(2)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12(α＋30°)－12×30°＝12α； ……………………………………………………………4分(3)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12(90°＋β)－12β＝45°；……6分 (4)∠MON 的大小等于∠AOB 的一半，而与∠BOC 的大小无关；……………9分(5)如图，设线段AB ＝a ，延长AB 到C ，使BC ＝b ，点M ，N 分别为AC ，BC 的中点，求MN 的长．规律是：MN 的长度总等于AB 的长度的一半，而与BC 的长度无关．…………12分。

初一数学期末考试试卷(2014.6)(满分100分,时间120分钟)一、选择题（本大题共10小题，每小题2分，共20分．） 1．下列运算正确的是（ ）A ．42226)3(y x xy =B ．xx 2121=- C ．527)()(x x x =-÷-D ．523523x x x =+2．已知一粒米的质量是0.000021千克，这个数字用科学记数法表示为 （ ） A ．41021-⨯千克 B ．6101.2-⨯千克 C ．5101.2-⨯千克 D ．4101.2-⨯千克 3．如图，能判定EB ∥AC的条件是（ ）A ．∠C ＝∠ABEB ．∠A ＝∠EBDC ．∠C ＝∠ABCD ．∠A ＝∠ABE 4．不等式x 2-≤6的解集在数轴上表示正确的是 （ ）A ．B ．C ．D ． 5．若152)2)(3(2-+=-+mx x n x x ，则 （ ）A ．5,1=-=n mB ．5,1-==n mC ．5,1-=-=n mD ．5,1==n m 6．如图，△ABC 中，∠ACB ＝90°，沿CD 折叠△CBD ，使点B 恰好落在AC 边上的点E 处．若∠A ＝22°，则∠BDC等于（ ）A ．44°B ．60°C ．67°D ．77°7．如图，A 、B 两点在数轴上表示的数分别是a 、b ，则下列式子中一定成立的是 （ ） A ．0>-b a B ．a ab 3< C ．b a 2121->- D ．b ab -> 8．如图，面积为6cm 2的△ABC 纸片沿BC 方向平移至△DEF 的位置，平移的距离是BC长的2倍，则△ABC纸片扫过的面积为（ ）A ．18cm 2B ．21cm 2C ．27cm 2D ．30cm 2第6题图 第7题图第3题图 第8题图 班级 姓名 考试号 .…………………………………………………………………………………………………………………………………………………10．下列说法：①一个多边形最多有3个锐角； ②n 边形有2)3(-n n 条对角线；③三角形的三条高一定交于一点；④当x 为任意有理数时，1062+-x x 的值一定大于1；⑤方程73=+y x 有无数个整数解．其中正确的有 （ ）A ．2个B ．3个C ．4个D ．5个 二、填空题（本大题共10小题，每空2分，共26分）11．计算：⑴122014--＝____________；⑵)1(22-x x ＝____________． 12．分解因式：42-y ＝____________．13．若一个多边形的内角和是外角和的2倍，则这个多边形的边数为____________． 14．命题“互为相反数的两个数的和为零”的逆命题是___________________________________． 15．已知32=+b a ，1-=ab ，则⑴2)(b a -＝____________；⑵)3)(3(--b a ＝____________．16．已知6=mx，3=n x ，则n m x -＝____________， n m x x -÷-2)(＝____________．17．若不等式组⎩⎨⎧>-<-ax x 012的解集是21<x ，则a 的取值范围是____________．18．如图，一个长方体的表面展开图中四边形ABCD 是正方形，则原长方体的体积是____________．19．一次生活常识竞赛一共有25道题，答对一题得4分，不答得0分，答错一题扣2分，小明有2题没答，竞赛 成绩要超过74分，则小明至多答错____________道题． 20．若二元一次方程组⎩⎨⎧=++=+my x m y x 232的解x ，y 的值恰好是一个等腰三角形两边的长，且这个等腰三角形的周长为7，则m 的值为____________． 三、解答题（本大题共8小题．共54分） 21．计算：（本题满分6分）⑴ 4322222)(23)(5a a b a b a b a ÷-+⋅-- ⑵2)2(2)32)(32(x y y x y x -----22．分解因式：(本题满分6分)⑴ 4824324-+-x x ⑵ )4()1(2)1(622b a x x a ----23．（本题满分8分）⑴解方程组：⎪⎩⎪⎨⎧-=+-=+-1532322y x y x ⑵解不等式组：⎪⎩⎪⎨⎧+≤-+<-2353)1(213xx x x 并写出它的D21EFDBA D A CB EF所有整数解．24．(本题满分6分)在正方形网格中，每个小正方形的 边长都为1个单位长度，△ABC 的三个顶点的位置 如图所示，现将△ABC 平移后得△EDF ，使点B 的 对应点为点D ，点A 对应点为点E ．（1）画出△EDF ； （2）线段BD 与AE 有何关系？____________；（3）连接CD 、BD ，则四边形ABDC 的面积为_______．25．（本题满分6分）如图，AD ∥BC ，∠A ＝∠C ，BE 、DF 分别平分∠ABC 和∠CDA ． 求证：BE ∥DF26．(本题满分7分)如图，△ABC 中，AD 是高，BE 平分∠ABC ． （1）若∠EBC ＝32°，∠1∶∠2＝1∶2，EF ∥AD ，求∠FEC 的度数；（2）若∠2＝50°，点F 为射线CB 上的一个动点，当△EFC 为钝角三角形时，直接写出∠FEC 的取值范围．27．（本题满分7分）如图①，将一副直角三角板放在同一条直线AB 上，其中∠ONM ＝30°，∠OCD ＝45°．（1）将图①中的三角板OMN 沿BA 的方向平移至图②的位置，MN 与CD 相交于点E ， 求∠CEN 的度数； 班级 姓名 考试号 .…………………………………………………………………………………………………………………………………………………（2）将图①中的三角板OMN绕点O按逆时针方向旋转，使∠BON＝30°，如图③，MN与CD相交于点E，求∠CEN的度数；（3）将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周，在旋转的过程中，在第_____________________秒时，直线MN恰好与直线CD 垂直．（直接写出结果）D28．（本题满分8分）某镇水库的可用水量为12000万立方米，假设年降水量不变，能维持该镇16万人20年的用水量．实施城市化建设，新迁入4万人后，水库只够维持居民15年的用水量．（1）问：年降水量为多少万立方米？每人年平均用水量多少立方米？（2）政府号召节约用水，希望将水库的保用年限提高到25年，则该镇居民人均每年需节约多少立方米才能实现目标？（3）某企业投入1000万元设备，每天能淡化5000立方米海水，淡化率为70%．每淡化1立方米海水所需的费用为1.5元，政府补贴0.3元．企业将淡化水以3.2元/立方米的价格出售，每年还需各项支出40万元．按每年实际生产300天计算，该企业至少几年后能收回成本（结果保留整数）？初一数学期末试题答案 2014.6 一选择题⒈ C ⒉C ⒊ D ⒋A ⒌D ⒍ C ⒎ C ⒏D ⒐ B ⒑ B二 填空题11. 0.5 ；x x 223- 12. )2)(2(-+y y 13. 6 14. 两个和为零的数互为相反数 15. 944；6 16. 2 ；108 17. a ≤21- 18. 12 19. 2 20. 2 三解答题21. ⑴原式=2242465a b a b a --………………（ 2）=224a b a -- ………………（ 3 ）⑵原式=)44(2492222x xy y x y +---………………（ 2 ）=xy x y 8622+- ………………（ 3 ）22. ⑴原式=)168(324+--x x ………………（ 1 ） =22)4(3--x ………………（ 2 ） =22)2()2(3-+-x x ………………（ 3 ）⑵原式=[])4(26)1(2b a a x --- ………………（ 1 ）=)84()1(2b a x +- ………………（ 2 ） =)2()1(42b a x +- ………………（ 3 ）23.⑴由①得823-=-y x ③ ………………（ 1 ） ②-③得y=1 ………………（ 2 ） 将y=1代入②得x=-2 ………………（ 3 ）∴⎩⎨⎧=-=12y x ………………（ 4 ）⑵由①得x ＜3 ………………（ 1 ） 由②得x ≥-1 ………………（ 2 ）∴-1≤x ＜3 ………………（ 3 ） ∴整数x=-1,0,1,2 ………………（ 4 ）24.⑴画图略 ；………………（ 2 ） ⑵ BD ∥═AE ；………………（ 4 ）⑶6 ………………（ 6 ）25.⑴∵AD ∥BC∴∠A+∠ABC=180°;∠C+∠ADC=180°………………（ 1） ∵∠A=∠C∴∠ABC=∠ADC ………………（ 2 ） ∵BE 、DF 分别平分∠ABC 和∠CDA∴∠EBC=21∠ABC, ∠EDF==21∠ADC ∴∠EBC=∠EDF ………………（ 4 ）∵AD ∥BC∴∠DFC=∠EDF∴∠EBC=∠DFC ………………（ 5 ） ∴BE ∥DF ………………（ 6 ）26.⑴∵BE 平分∠ABC ∴∠ABC=2∠EBC=64° ………………（ 1 ） ∵AD 是高 ∴AD ⊥BC ∴∠ADB=90°∴∠1=90°−∠ABC=26° ………………（ 2 ） ∵∠1∶∠2＝1∶2 ∴∠2=2∠1=52° ………………（ 3 ） ∵EF ∥AD∴∠FEC=∠2=52° ………………（ 4 ）⑵90°＜∠FEC ＜140°; 0°＜∠FEC ＜50°………………（ 7 ） （ 做对一个答案仅得1分）27⑴∠CEN=180°-∠ONM −∠NCD=180°-30°-45°=105°………………（ 1 ） ⑵∵∠N=∠BON ＝30°∴MN ∥CO ………………（ 2 ） ∴∠CEN+∠OCD ＝180°∴∠CEN ＝180°−∠OCD =135° ………………（ 3 ） ②5.5秒，11.5秒 ………………（ 7 ） （ 做对一个答案得2分）28.解：（1）设年降水量为x 万m 3，每人年平均用水量为ym 3，由题意得，， ………………（ 1 ）解得：．答：年降水量为200万m 3，每人年平均用水量为50m 3．………………（ 3 ）（2）设该镇居民人均每年需用水z m 3水才能实现目标， 由题意得，12000+25×200=20×25z ， 解得：z=34，50﹣34=16m 3．答：设该镇居民人均每年需节约16 m 3水才能实现目标．………………（ 5 ）（3）设该企业n 几年后能收回成本，由题意得，[3.2×5000×70%﹣（1.5﹣0.3）×5000]×﹣40n≥1000，………………（ 6 ）解得： 29188n ∴最小整数n=9答：至少9年后企业能收回成本． ………………（ 8）。

211133x ax +-+>2013-2014学年度第二学期人教版七年级数学期末模拟试卷（最新版）一、填空题(每题3分、共30分)1. 下列实数722，π-，14159.3，21中无理数有（ ） Ａ．2个 Ｂ．3个 Ｃ．4个 Ｄ．5个2. 下列各组数中互为相反数的是（ ）A.－2－2C.－2 与12-D.2与2-3.为了了解某校1500名学生的体重情况，从中抽取了100名学生的体重，就这个问题来说，下面说法正确的是（ ）(A)1500名学生的体重是总体 (B)1500名学生是总体(C)每个学生是个体 (D)100名学生是所抽取的一个样本 解集是x ＜35，则a 应满足（ ） 4. 不等式的Ａ．5a >Ｂ．5a =Ｃ．5a >-Ｄ．5a =-5. 点M （a ，a-1）不可能在（ ）A. 第一象限B. 第二象限C. 第三象限D. 第四象限 6、下列说法中错误的个数是（ ）（1）过一点有且只有一条直线与已知直线平行。

（2）过一点有且只有一条直线与已知直线垂直。

（3）在同一平面内，两条直线的位置关系只有相交、平行两种。

（4）不相交的两条直线叫做平行线。

（5）有公共顶点且有一条公共边的两个角互为邻补角。

A. 1个 B. 2个 C. 3个 D. 4个7、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y=kx+b 的解，则k 与b 的值为（ ）（A ）21=k ，b=-4；（B ）21-=k ，b=4；（C ）21=k ，b=4；（D ）21-=k ，b=-4 8．三角形A’B’C’是由三角形ABC 平移得到的，点A （－1，－4）的对应点为A ’（1，－1），则点B （1，1）的对应点B ’、点C （－1，4）的对应点C ’的坐标分别为（ ） A 、（2，2）（3，4） B 、（3，4）（1，7） C 、（－2，2）（1，7） D 、（3，4）（2，－2）9.不等式组的解集是x ＞2，则m 的取值范围是( )．(A)m ≤2 (B)m ≥2 (C)m ≤1 (D)m ≥110．如右图所示，点E 在AC 的延长线上，下列条件中能判断CD AB //（ ）A. 43∠=∠B. 21∠=∠C. DCE D ∠=∠D.180=∠+∠ACD D二、填空题（每题3分，共24分）11、在扇形统计图中，其中一个扇形的圆心角是216°，则这年扇形所表示的部分占总体的百分数是 .12.如果一个数的平方根是6+a 和152-a ，则这个数为 。

2013-2014学年度七年级下数学期末试卷（新人教版）一．选择题.（本大题共10小题，每小题3分，共30分. ）1.在数－3.14, 2, 0, π, 16, 0.1010010001……中无理数的个数有 （ ）A 、3个B 、2个C 、1个D 、4个2.下列说法正确的是（ ）A 、同位角相等;B 、在同一平面内，如果a ⊥b ，b ⊥c ，则a ⊥c 。

C 、相等的角是对顶角;D 、在同一平面内，如果a ∥b,b ∥c ，则a ∥c 。

3.列说法正确的是（ ）A 、 a、aC的平方根是0.1 D4. 如图，下列条件中不能判定AB∥CD 的是（ ）A.∠3＝∠4B.∠1＝∠5C.∠1＋∠4＝180°D.∠3＝∠55.为保护生态环境，陕西省某县响应国家“退耕还林”号召，将某一部分耕地改为林地，改变后，林地面积和耕地面积共有180平方千米，耕地面积是林地面积的25%，为求改变后林地面积和耕地面积各多少平方千米。

设改变后耕地面积x 平方千米，林地地面积y 平方千米，根据题意，列出如下四个方程组，其中正确的是（ ）A ⎩⎨⎧⋅==+%25180x y y xB ⎩⎨⎧⋅==+%25180y x y x C ⎩⎨⎧=-=+%25180y x y x D ⎩⎨⎧=-=+%25180x y y x 6.下列调查中，适合用普查（全面调查）方法的是（ ）.A.电视机厂要了解一批显像管的使用寿命；B.要了解我市居民的环保意识；C.要了解我市“阳山水蜜桃”的甜度和含水量；D.要了解某校数学教师的年龄状况. 7.不等式组⎩⎨⎧>--<32x x 的解集是（ ）A.x<－3B.x<－2C.－3<x<－2D.无解8.2014年某市有23000名初中毕业生参加了升学考试，为了解23000 名考生的升学成绩，从中抽取了200名考生的试卷进行统计分析，以下说法不正确的是（ ） A ．23000名考生的成绩是总体 B ．每名考生是个体C ．200名考生的成绩是总体的一个样本D ．每名考生的成绩是个体9.某种商品的进价为80元，出售时标价为120元，后来由于该商品积压，商店准备打折出售，但要保证利润率不低于5%，则至多可打（ ）A ．六折B ．七折C ．八折D ．九折10. 若不等式组⎩⎨⎧->+<+1472,03x x a x 的解集为0<x ，则a 的取值范围为( )A a ＞0 B. a ＝0 C. a ＞4 D. a ＝4 二、填一填 （本大题共10小题，每小题3分，共30分.） 11. 16的算术平方根是____________;12、如图，如果 AB ∥CD ，则∠___=∠_____；如果∠3=∠4，则______∥_________。

苏州市相城区2013－2014学年第二学期期末考试七年级数学试卷2014.06本试卷由填空题、选择题和解答题三大题组成，共28题，满分130分。

考试用时120分钟。

注意事项：1．答题前，考生务必将学校、姓名、考场号、座位号、考试号填写在答题卷相应的位置上．2．答题必须用0.5mm黑色墨水签字笔写在答题卷指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题．3．考生答题必须在答题卷上，答在试卷和草稿纸上一律无效，一、选择题：（本大题共有10小题，每小题3分，共30分，以下各题都有四个选项，其中只有一个是正确的，选出正确答案，并在答题卡上将该项涂黑°）1．一个多边形的每个外角都等于60°，则此多边形是A．三边形B．四边形C．五边形D．六边形2．下列命题中，属于真命题的是A．面积相等的三角形是全等三角形B．同位角相等C．若a＝b，则a＝b D．如果直线l1∥l2，直线l2∥l3，那么l1∥l33．若△ABC≌△DEF，△ABC的周长为100cm，DE＝30cm，DF＝25cm，那么BC长A．55cm B．45cm C．30cm D．25cm4．下列四个多项式，哪一个是2x2＋5x－3的因式?A．2x－1 B．2x－3 C．x－1 D．x－35．从下列不等式中选择一个与x＋1≥2组成不等式组，若要使该不等式组的解集为x≥1，则可以选择的不等式是A．x>0 B．x>2 C．x<0 D．x<26．计算25m÷5m的结果为A．5 B．5m C．20 D．20m7．如果(x＋1)(x2－5ax＋a)的乘积中不含x2项，则a为A．5 B．15C．－15D．－58．根据以下对话，可以求得小红所买的笔和笔记本的价格分别是A．0.8元／支，2.6元／本B．0.8元／支，3.6元／本C．1.2元／支，3.6元／本D．1.2元／支，2.6元／本9．如图，在△ABC中，AB＝AC，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，则下列说法：①DA平分∠EDF；②AE＝AF，DE＝DF；③AD 上任意一点到B 、C 两点的距离相等；④图中共有3对全等三角形，其中正确的有A ．4个B ．3个C ．2个D ．1个10．已知关于x ，y 的方程组343x y a x y a +=-⎧⎨-=⎩，其中－3≤a ≤1，给出下列结论：①当a ＝1时，方程组的解也是方程x ＋y ＝4－a 的解；②当a ＝－2时，x 、y 的值互为相反数；③若x≤1，则1≤y ≤4；④51x y =⎧⎨=-⎩是方程组的解，其中正确的是 A ．①② B ．③④ C ．①②③ D ．①②③④二、填空题：（本大题共8小题，每小题3分，共24分，把答案直接填在答题卡相对应的位置上)11．计算：(12)0的结果是 ▲ ． 12f 命题“相等的角是对顶角”的逆命题是 ▲ ．13．如图，C 岛在A 岛的北偏东50°方向，C 岛在B 岛的北偏西40°方向，则从C 岛看A ，B 两岛的视角∠ACB 等于 ▲ ．14．若一多项式除以2x 2－3，得到的商式为x ＋4，余式为3x ＋2，则此多项式为 ▲ ．15．不等式13（x －m ）>3－m 的解集为x>1，则m 的值为 ▲ ．16．如图，△\ABC 的周长为28cm ，把△ABC 的边AC 对折，使顶点C 和点A 重合，折痕交BC 边于点D ，交AC 边于点E ，连接AD ，若AE ＝4cm ，则△ABD 的周长是 ▲ cm ．17．为确保信息安全，信息需加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文a ，b ，c ，d 对应密文3a ＋b ，2b ＋c ，2c ＋d ，2d ．例如，明文1，2，3，4对应密文5，7，10，8．当接收方收到密文14，9，24，28时，则解密得到的明文四个数字之和为 ▲ ．18．如图，在△ABC 中，AB ＝AC ＝10厘米，∠B ＝∠C ，BC ＝8厘米，点D为AB 的中点，如果点P 在线段BC 上以3厘米，秒的速度由B 点向C点运动，同时点Q 在线段CA 上由C 点向A 点运动，当一个点停止运动时，另一个点也随之停止运动，当点Q 的运动速度为 ▲ 时，能够在某一时刻使△BPD 与△CQP 全等．三、解答题：（本大题共10小题，共76分．把解答过程写在答题卡相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明）．19．（本题满分8分，每小题4分）计算：(1)()3242a a a ∙+-； (2)301211320.250.54⨯⨯．20．（本题满分8分，每小题4分）解方程组：(1)3725x y x y -+=⎧⎨=⎩ (2)3005%53%30025%x y x y +=⎧⎨+=⨯⎩21．（本题满分5分）如图，EF∥AD，∠1＝∠2，∠BAC＝80°，将求∠AGD的过程填写完整．∵EF//AD，∴∠2＝▲( ▲)又∵∠1＝∠2，∴∠1＝∠3( ▲)∴AB// ▲( ▲)∴∠BAC＋▲＝180°( ▲)∵∠BAC＝80°，∴∠AGD＝▲．22．（本题满分8分，每小题4分）因式分解：(1)x3－4x；(2)（x－1）（x－4）－10．23．（本题满分8分）解不等式（或不等式组）：(1)解不等式1332x x+<(2)解不等式组()320211132x xxx⎧--≥⎪⎨->-⎪⎩24．（本题满分7分）如图，∠A＝∠C＝54°，点B在AC上，且AB＝EC，AD＝BC，BF⊥DE于点F．(1)证明：BD＝BE；(2)求∠DBF的度数．25．（本题满分7分）已知三元一次方程组5123 x yx zy z+=⎧⎪+=-⎨⎪+=-⎩(1)求该方程组的解；(2)若该方程组的解使ax＋2y＋z<0成立，求整数a的最大值．26．（本题满分8分）我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小．而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一，所谓“作差法”：就是通过作差、变形，并利用差的符号来确定它们的大小，即要比较代数式M、N 的大小，只要作出它们的差M－N，若M－N>0，则M>N；若M－N＝0，则M＝N．若M －N<0，则M<N，请你用“作差法”解决以下问题：(1)如图，试比较图①、图②两个矩形的周长C1、C2的大小(b>c)．(2)如图③，把边长为a＋b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形的面积之和S1与两个矩形面积之和S2的大小．27．（本题满分8分）第一中学组织七年级部分学生和老师到苏州乐园开展社会实践活动，租用的客车有50座和30座两种可供选择．学校根据参加活动的师生人数计算可知：若只租用30座客车x辆，还差5人才能坐满；(1)则该校参加此次活动的师生人数为▲（用含x的代数式表示）；(2)若只租用50座客车，比只租用30座客车少用2辆，求参加此次活动的师生至少有多少人？(3)已知租用一辆30座客车往返费用为400元，租用一辆50座客车往返费用为600元，学校根据师生人数选择了费用最低的租车方案，总费用为2200元，试求参加此次活动的师生人数．28．（本题满分9分）如图1，已知正方形ABCD，把一个直角与正方形叠合，使直角顶点与一重合，当直角的一边与BC相交于E点，另一边与CD的延长线相交于F点时．(1)证明：BE＝DF；(2)如图2，作∠EAF的平分线交CD于G点，连接EG．证明：BE＋DG＝EG；(3)如图3，将图1中的“直角”改为“∠EAF＝45°”，当∠EAF的一边与BC的延长线相交于E点，另一边与CD的延长线相交于F点，连接EF．线段BE，DF和EF之间有怎样的数量关系？并加以证明．。

2013—2014下学期七年级期中考试数学试题一、选择题（每题3分，共30分）1、下列各数中，介于6和7之间的是 （ ） A 、38 B 、43 C 、58 D 、31002、 如图A B ∥CD ，∠A =70°，则∠1的度数为 （ ） A 、70°B 、100°C 、110°D 、130°3、如果点P （m,4）在第二象限，那么点Q （4，-m ）在 （ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限4、点E 在AC 的延长线上，下列条件能判断A B ∥CD 的 （ ） A 、∠3=∠4 B 、∠1=∠2 C 、∠D=∠DCE D 、∠D+∠ACD=180°5、下列说法正确的是： （ ） A 、64的立方根是4 B 、2的平方根是2 C 、平方根等于它本身的数是1和0D 、无限小数都是无理数6、若点M （-3，-5）向下平移7个单位长度得到M 1，则M 1的坐标为（ ） A 、（-3,2） B 、（-3,-12） C 、（4,-5） D 、（-10,-5）7、下列计算正确的是 （ ）A 、525±=B 、3)3(2-=- C 、37＞2 D 、3.009.0±=±8、下列命题：①相等的角是对顶角②在同一平面内，a 、b 、c 是三条直线，若a ∥b ，b ∥c ， 则a ∥c ③两条直线被第三条直线所截同位角相等 其中假命题有 （ ） A 、0个 B 、1个 C 、2个 D 、3个 9、16的平方根是 （ ）A 、4B 、±4 2 D 、±210、已知a ∥b ，若∠1=70°，∠2=140°则∠3的度数为 （ ） A 、105° B 、100° C 、115° D 、110°AEC1ABC D 3 12ab二、填空题（每题3分，共30分） 11、41的算术平方根是___________________ 12、－5的相反数_________, 2－5的绝对值是___________ 13、把下列命题改写成“如果…，那么…”的形式：等角的补角相等：____________________________________________________________ 14、点P （-3,5） 到y 轴的距离是_________15、已知1.1001.102=，则=0201.1_______________ 16、一个正数的平方根是2a-3和5-a ，则a=_________ 17、下列各数中：0.4583， ∙7.3， π-， 71-， 2-， 0， 327-_____________________________ 是无理数 18、若0)3(2=+++y y x ，则xy=_____________19、如图，有一块长22米，宽10米的草坪，其中有两条宽2米的直道把草坪分成4块，则草坪的面积是_____________ 平方米20、如图，将一矩形纸片ABCD 沿EF 折叠，使顶点C 、D 分别落在C ′、D ′处，C ′E 交AF 于点G,若∠CEF=70°，则∠GFD ′=_______________ 三、解答题21、计算（每题5分，共10分） （1） 41809.03--- （2）2322--22、求下列各式中的x （每题5分，共10分）（1）0027.03=-x （2）9)2(2=-x23、（8分）如图：在平面直角坐标系中，已知点O （0，0）A （0,:4），点B 在x 轴上，且三角形AOB 的面积是3，求点B 的坐标。