第三章 静态电磁场II ：恒定电流的电场和磁场3．1 恒定电场的基本方程与场的特性1．恒定电场由麦克斯韦组的磁场旋度方程，对于导电媒质中的传导电流密度J c ，有c J H =⨯∇上式两边取散度，得c =•∇J又由麦克斯韦组的另一旋度方程=⨯∇E而导电媒质的构成方程为E J γ=c由此可见，导电媒质中(电源区域外)恒定电场具有无散无旋场。
仿照静电场的处理，引入标量电位函数ϕ(r )作为辅助场量，即令E = -∇ϕ ，可得电位ϕ满足拉普拉斯方程，即∇2ϕ = 0例1：设一扇形导电片，如图所示，给定两端面电位差为U 0。
试求导电片内电流场分布及其两端面间的电阻。
[解]：采用圆柱坐标系，设待求场量为电位ϕ，其边值问题为：()()⎪⎪⎪⎩⎪⎪⎪⎨⎧==∈=∂∂⋅=∇==0022220,01,,U Dz θφφϕϕφρφϕρφρϕ积分，得ϕ =C 1φ + C 2由边界条件，得θ1U C =， 02=C图 扇形导电片中的恒定电流场故导电片内的电位 φθϕ⎪⎭⎫ ⎝⎛=0U电流密度分布为φφρθγθφφργϕγγe e E J 00U U -=⎪⎭⎫⎝⎛∂∂⋅-=∇-== 对于图示厚度为t 的导电片两端面的电阻为()⎪⎭⎫ ⎝⎛=-⋅-=•==⎰⎰a b t td U U d U I U R baS0ln γθρρθγφφe e SJ2．电功率在恒定电流场中，沿电流方向截取一段元电流管，如图所示。
该元电流管中的电流密度J 可认为是均匀的，其两端面分别为两个等位面。
在电场力作用下，dt 时间内有dq 电荷自元电流管的左端面移至右端面，则电场力作功为dW = dU ⨯ dq于是外电源提供的电功率为()()EJdV d d dI dU dtdqdU dt dW dP =•⨯•=⨯=⨯==S J l E 故电功率体密度γγ22d d J E EJ V P p ==== 或写成一般形式p = E •J3．不同媒质分界面上的边界条件 两种不同导电媒质分界面上的边界条件：类同于静电场的讨论，在两种不同导电媒质分界面上场量的边界条件为J 1n = J 2n 或 e n ⋅(J 2-J 1)=0 E 1t = E 2t 或 e n ⨯(E 2-E 1)=0对于线性且各向同性的两种导电媒质，有如下类比于静电场的折射定律2121tg tg γγαα= 图 电功率的推导良导体与不良导体分界面上的边界条件：当电流从良导体流向不良导体时，如图所示，设γ1 >>γ2，由折射定律可知，只要α1 ≠ 90︒，就有α2 ≈ 0。
这表明，当电流由良导体侧流向不良导体侧时，电流线总是垂直于不良导体(α2≈0)。
换句话说，这时可以不计良导体内部的电压降，而把良导体表面可近似看作为等位面。
导体与理想介质分界面上的边界条件：此时，由于J c2n = 0，必然有J c1n = 0；且E 1t = E 2t ，电场强度的切向分量连续。
应指出的是，虽然E 1n =J c1n /γ1= 0，但E 2n ≠ 0，其结果将使导体外表面处的电场强度E 2，与导体表面不相垂直，如图所示。
然而，分量E 2t 与E 2n 相比是极其微小的，因而在研究导体外表面附近的电场时，可以略去E 2t 分量的影响。
即近似为静电场中导体的边界条件。
也就是说，当分析载有恒定电流的导体外部电场时，可以应用静电场分析方法。
两种有损电介质分界面上的边界条件： 如图所示，在两种有损电介质的分界面上，应有n n E E 2211γγ=同时，还有σεε=-n n E E 1122联立求解，得分界面上自由电荷面密度为图 由良导体(γ1)到不良导体(γ2)的电流流向图 输电线电场示意图2图两种有损电介质的分界面2n J 2212112γγγεγεσ-=由此可见，只有当两种媒质参数满足2112γεγε=条件时，其上表面自由电荷才为零，即σ=0。
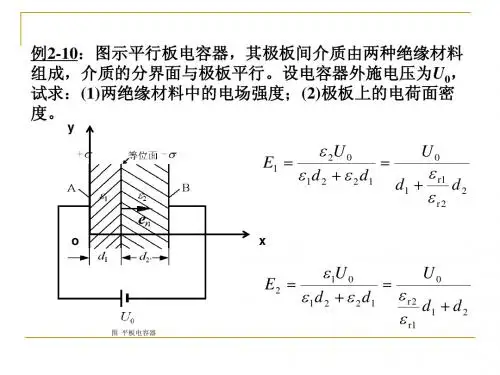
例2：设一平板电容器由两层非理想介质串联构成，如图所示。
其介电常数和电导率分别为ε1，γ1和ε2，γ2，厚度分别为d 1和d 2，外施恒定电压U 0，忽略边缘效应。
试求：(1)两层非理想介质中的电场强度；(2)单位体积中的电场能量密度及功率损耗密度；(3)两层介质分界面上的自由电荷面密度。
[解]：(1) 忽略边缘效应，可以认为电容器中电流线与两介质交界面相垂直，用边界条件2211E E γγ=又有电压关系02211U d E d E =+联立求解两式，得1221021d d U E γγγ+=， 1221012d d U E γγγ+=(2)两非理想介质中的电场能量密度分别为211211e E w ε=， 222212e E w ε= 相应的单位体积中的功率损耗分别为2111E p γ=， 2222E p γ=(3)分界面上的自由电荷面密度为0122121122212112U d d J γγγεγεγγγεγεσ+-=-=3．2 恒定电场与静电场的比拟1．静电比拟法将均匀导电媒质中的恒定电场与无源区中均匀介质内的静电场相比较，可以看出，两者有如下表的对应关系。
图 非理想介质的平板电容器中的恒定电流场21显然，只要两者对应的边界条件相同，则恒定电流场中电位ϕ、电场强度E 和电流密度J c 的分布将分别与静电场中的电位ϕ、电场强度E 和电位移矢量D 的分布相一致。
如果场中两种媒质分区均匀，当恒定电场与静电场两者边界条件相似，且两者对应的电导率与介电常数之间满足如下物理参数相似的条件时：2121εεγγ= 则两种场在分界面上的J c 线与对应的D 线折射情况相同。
根据以上相似原理，就可以把一种场的计算和实验结果，推广应用于另一种场。
这就是静电比拟法。
由静电比拟法，有εγ=C G 因此，可以利用电容的计算方法计算电导或电阻，反之亦然。
即⎰⎰⎰⎰••=••==lSlS d d d d UI G lE SE l E SJγc⎰⎰⎰⎰••=••==lSlSd d d d Uq C lE SE lE SD ε例1：内外导体半径分别为a 和b 的同轴电缆，如图所示导体间外施电压U 0。
试求其因绝缘介质不完善而引起的电缆内的泄漏电流密度及其单位长绝缘电阻。
图 同轴电缆中的泄漏电流[解]：（1）解法一：恒定电场分析法电场强度E 和泄漏电流密度J c 均只有径向分量，作一半径为ρ的同轴单位圆柱面，且令单位长泄漏电流为I ，则πρ2I J c =， πργ2I E =内外导体间电压为ab I E U U baln 2d 0AB γρπ===⎰ 由此可知泄漏电流密度为ρργe J ab U ln0c =()b a <<ρ电缆的单位长绝缘电阻为abI U R ln 210γπ===（2）解法二：静电比拟法在同轴电缆分析中，已求得电场强度为ρ0abU e E lnρ=()b a <<ρ故泄漏电流密度ρab U e E Jc lnργγ==()b a <<ρ同理，单位长电导可以由单位长度电容求得，即电缆的单位长绝缘电阻为ab C G R ln 2111γγεπ=⋅==2．接地电阻接地技术是保障人身和设备的一项电气安全措施。
计算接地体的接地电阻是恒定电场计算的一项重要工作。
下面计算图示埋于大地的半球形接地体的接地电阻。
由镜象法得：⎰∞====a 2a21dr r 2i i 1i u G 1R πγγπ3．跨步电压电力系统接地体一旦有电流通过，由于接地电阻的存在，在地面上存在电位分布。
此时，人体跨步的两足之间的电压称为跨步电压。
当跨步电压超过允许值时，将威胁人的生命。
对于如图所示的半球形接地器，由镜象法，地面上任意点P 的电位为()r 2Idr r 2I d r2γγϕπ=π=•=⎰⎰∞∞Pr E r 如图绘出了地面电位分布。
设人的跨步距离为b ，在距半球中心距离r 点的跨步电压为2rbr r 2Ibr 1b r 12I dr r 2I d U γγγπ≈⎪⎭⎫ ⎝⎛--π=π=•=⎰⎰-BAAB l E 设U 0为人体安全的临界跨步电压（通常小于50~70V ），可以确定危险区半径r 0为02U Ibr γπ=3．3 恒定磁场的基本方程与场的特性1．恒定磁场的基本方程由麦克斯韦方程组，描述恒定磁场的基本方程为c J H =⨯∇0=•∇B(a) 电流线J 的分布 (b) 镜象法图示图 半球形接地器γ土壤 γ土壤aai2iγ土壤ao brIJϕA B aIγπ2 rP图 跨步电压与危险区的分析r E 22rIγπ=I 图 环量⎰•ll B d 与激磁电流I 间关系说明图媒质的构成方程为 H B μ=2．恒定磁场的有旋性在自由空间中，由基本方程可以得出，在恒定磁场问题磁感应强度矢量B 与传导电流密度J c 之间的关系为c 0J B μ=⨯∇上式表明，源于电流的磁场具有旋涡场的特性，表明了磁力线与电流源之间相互交链的基本特征。
利用斯托克斯定理，得安培环路定律：∑⎰⎰==•=•n1k k 0S0lI d d μμS J l B c式中，电流I k 正负，取决于电流方向与积分回路绕行方向是否符合右手定则。
当方向相符时为正；反之取负值。
如图，有：)(321lI I Id -+=•⎰μl B3．恒定磁场的无散性基本方程还表明了恒定磁场的磁感应强度的散度处处为零，具有无散(无源)性。
磁力线是无头无尾的闭合曲线，即磁通连续性原理。
4．矢量磁位的引入由亥姆霍兹定理，磁感应强度B (r )应为)()()(r A r r B ⨯∇+-∇=ϕ式中()⎰'=''-'•∇'π=V 0V d 41r r r B r )(ϕ ()()⎰⎰⎰''''π=''-π=''-'⨯∇'π=V c 0V c 0V V d R4V d 4V d 41J r r J r r r B r A μμ 式中A 称为矢量磁位。
在SI 单位制中，矢量磁位的单位是韦伯/米(Wb/m )。
需要说明的是矢量磁位A 不是一个物理量，不能被测量，仅是一个为简化计算引入的数学上的辅助矢量函数。
对于不同形式的电流源，有：体电流J c ： ()⎰'''π=V0V d R4r J r A c μ)(面电流K ： ()⎰'π='')(S 0dS R4r K r A μ 线电流I ： ⎰π='')(l 0Rd 4I l r A μ5．磁感应强度表达式上段讨论表明，自由空间中任意点的磁感应强度等于该点矢量函数A 的旋度。
若已知J c (r )，可以先计算矢量磁位A ，然后再通过计算A 旋度计算磁感应强度B 。
