下载文档原格式
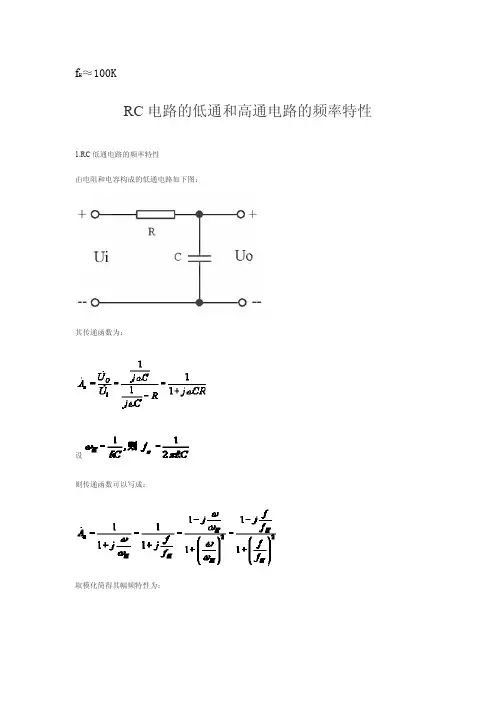
f H≈100KRC电路的低通和高通电路的频率特性1.RC低通电路的频率特性由电阻和电容构成的低通电路如下图：其传递函数为：设则传递函数可以写成：取模化简得其幅频特性为：相频特性为：从其幅频特性曲线如下图，可以看出，当频率f升高时，|Au|逐渐下降，当f=f H时，|Au|=1/√2=0.707，所以我们称f H为低通滤波的上限截止频率，其通频带为0~f H。
因电路只有一个储能元件，所也也称一阶低通滤波电路。
工程上为了作图简便，常用波特图表示，如下图，其中细实线为实际曲线，粗实线为实际曲线的渐近线。
当f≤0.1f H时，近似认为|Au|≈1，即|Au|=(20lg|Au|)dB=0dB当f≥10f H时，近似认为|Au|=1/（f/f H）,也即|Au|≈20lg（f H/f）根据上图可以看出，当f≤0.1f H时，幅频物性的波特图为一条水平线，当f≥10f H时是一条-20dB/十倍频的斜线，两线在f=f H处相交，因此f H也称为转折频率。
在粗略计算时，可以用渐近线代替实际曲线，最大误差发生在f H处，误差为|20lg0.707|dB=20×0.15dB=3dB。
当f≤0.1f H时，相频特性曲线，可以看成φ=0的近似线，当f≥10f H时，近似认为φ=-90，当f=f H时，φ=-45。
在0.1f H<f<10f H区域内，可用一条斜率为-45/十倍频的斜线代替。
其中f=0.1f H和f=10f H误差最大，为5.7度。
2.RC高通电路的频率特性电如如下图：其传递函数为：设由传递函数可写成：取模得其幅频特性：相频特性为：根据其特性可以绘出RC高通电路的波特图其下限截止频率为f L ，通频带为f L ~∞。
为一阶高通滤波。
综合上述的低通和高通滤波电路，它们对信号只有衰减作用，没有放大作用，因些称为无源滤波电路。
上述两种电路常用在有源滤波电路中，在电子分频的音响功放中也比较常见，比如我们可用上述电路，把音响的输入信号二分频后分别进行放大，来代替昂贵的分频器。
实验6 RC网络频率特性的研究1 、实验目的（ 1 ）掌握幅频特性和相频特性的测试方法。
（ 2 ）加深理解常用 RC 网络幅频特性和相频特性的特点。
（ 3 ）学习“分贝”的概念，并用它来绘制频率特性曲线。
（ 4 ）借助 RC 网络对非正弦信号作实验分析。
2 、原理说明图4-6-1 二端口RC网络RC 网络的频率特性可用网络函数来描述。
图 4-6-1 中二端口 RC 网络，若在它的输入端口加频率可变的正弦信号（激励）1，则输出端口有相同频率的正弦输出电压（响应）2。
网络的电压传输比为：幅频特性|H(jω)｜和相频特性φ(ω) 统称为网络的频率响应（频率特性）。
（1） RC 低通网络图 4-6-2(a)所示为 RC 低通网络。
它的网络函数为:图4-6-2 Rc低通网络及其频率特性其中为幅频特性，显然它随着频率的增高而减小，说明低频信号可以通过，高频信号被衰减或抑制。
当ω =1/RC 时，即于是有 U2/U1=0.707 ，于是有：通常把 U2降低到 0.707U1时的角频率ω称为截止角频率ωc ，即：ω=ωc=1/RC图 4-6-2(b),(c)分别为 RC 低通网络的幅频特性曲线和相频特性曲线。
（2） RC 高通网络图 4-6-3(a)所示为 RC 高通网络。
它的网络函数为可见，随着频率的降低而减小，说明高频信号可以通过，低频信号被衰减或被抑制。
网络的截止频率仍为ωc=1/RC ，因为ω= ωc时，|H(j ω )｜=0.707 。
它的幅频特性和相频特性分别如图4-6-3 （b）、（c） 所示。
图4-6-3 RC高通网络及其频率特性（3） RC 带通网络（ RC 选频网络）图 4-6-4 （a）所示为 RC 带通网络。
它的网络函数：显然，当信号频率ω=1/RC 时，对应的模｜H(jω)｜ =1/3 为最大，信号频率偏离ω=1/RC 越远，信号被衰减和阻塞越厉害。
说明该 RC 网络允许以ω = ω0=1/RC( ≠0) 为中心的一定频率范围（频带）内的信号通过，而衰减或抑制其它频率的信号，即对某一窄带频率的信号具有选频通过的作用，因此，将它称为带通网络，或选频网络。
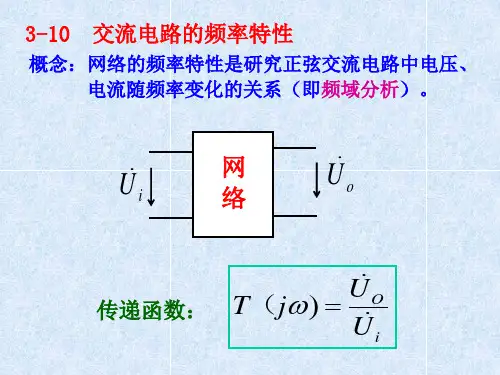
实验3 RC 网络频率特性研究一、实验原理1. 网络频率特性的定义网络的响应相量与激励相量之比是频率ω的函数，称为正弦稳态下的网络函数。
表示为)()()(ωϕωωj e j H j H ==激励向量响应向量其模随频率ω变化的规律称为幅频特性，辐角随ω变化的规律称为相频特性。
为使频率特性曲线具有通用性，常以ω作为横坐标。
通常，根据随频率ω变化的趋势,将RC 网络分为“低通(LP )电路”、“高通(HP )电路”、“带通(BP )电路”、“带阻(BS )电路”等。
2．典型RC 网络的频率特性 (1) RC 低通网络图S3-1(a)所示为RC 低通网络。
它的网络函数为RCj C j R C j U U j H i ωωωω+=+==11/1/1)(0 其模为： 2)(11)(RC j H ωω+=辐角为：)arctan()(RC ωωϕ-=显然，随着频率的增加， )(ωj H 将减小，这说明低频信号可以通过，高频信号被衰减或抑制。
当ω=1/RC ，即707.0/=i o U U ，通常把o U 降低到0.707 i U 时的角频率ω称为截止角频率C ω。
即RC C /1==ωω(a) RC 低通网络 (b) 幅频特性 (c) 相频特性图S3-1 RC 低通网络及其频率特性(2) RC 高通网络图S3-2 (a)所示为RC 高通网络。
它的网络传递函数为RCj R RU U j H i ωω/1)(0+== 其模为： 2)1(11)(RCj H ωω+=辐角为： )arctan(90)(0RC ωωϕ-=可见，随着频率的降低而减小，说明高频信号可以通过，低频信号被衰减或抑制。
网络的截止频率仍为RC C /1=ω，因为ω=C ω时，|H(j ω)| =0.707。
它的幅频特性和相频特性分别如图S3-2(b)、(c)所示。
-iU(ϕω9045ω(a) RC高通网络（b)幅频特性(C)相频特性(a) RC 高通网络 (b) 幅频特性 (c) 相频特性图S3-2 RC 高通网络及其频率特性(3) RC 串并联网络（RC 带通网络）图S3-3(a)所示为RC 串并联网络。
RC网络频率特性和选频特性的研究（综合实验）实验目的1学会已知电路性能参数的情况下设计电路（元器件）参数；2 .用仿真软件Mutualism研究RC串、并联电路及RC双T电路的频率特性;3.学会用交流毫伏表和示波器测定RC网络的幅频特性和相频特性；4•理解和掌握低通、高通、带通和带阻网络的特性5.熟悉文氏电桥电路的结构特点及选频特性。
、实验设备（记录所用设备的名称型号编号）将实验中自选的仪器设备和元件列表，并记录型号、规格、数量和编号等电路的频域特性反映了电路对于不同的频率输入时，其正弦稳态响应的性质，一般用电路的网络函数H（j，）表示。
当电路的网络函数为输出电压与输入电压之比时，又称为电压传输特性。
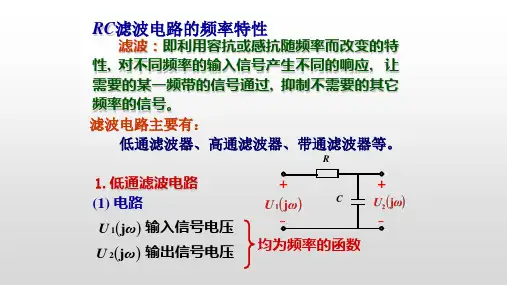
即：1低通电路图431低通滤波电路图432 低通滤波电路幅频特性简单的RC滤波电路如图小！，输出为U2时，构成的是低通滤波电路。
因为：所以：H （j ）是幅频特性，低通电路的幅频特性如图，在川=1 RC时，H（j⑷）=厂20 .,7即U2/U1 =0.707，通常U2降低到0.707山时的角频率称为截止频率，记为-'0。
2.高通电路图图433高通滤波电路图434高通滤波电路的幅频特性所以：其中H（j「）传输特性的幅频特性。
电路的截止频率-，0 = 1 RC高通电路的幅频特性如当0时，即低频时当'■ ■ > '-0时，即高频时，H j \=1 o3.研究RC串、并联电路及RC双T电路的频率特性；4.文氏电桥电路的结构特点及选频特性。
四、实验方法测量频率特性用逐点描绘法”，图，在图中：图4.3.5测量方法图4.3.6测量相频特性方法测量幅频特性：保持信号源输出电压（即RC网络输入电压）U j恒定，改变频率f，用交流毫伏表监视U i，并测量对应的RC网络输出电压U o，计算出它们的比值A = U o. U i , 然后逐点描绘出幅频特性。
测量相频特性：保持信号源输出电压（即RC网络输入电压）U j恒定，改变频率f,,用交流毫伏表监视U i，用双踪示波器观察U0和U j波形，如图，若两个波形的延时 .讥，周期为T，则它们的相位差® =360°汉A t/T ,，然后逐点描绘出相频特性。
实验七 RC 电路频率特性一、实验目的1、了解低通和高通滤波器的频率特性，熟悉文氏电桥的结构特点及选频特性；2、掌握网络频率特性测试的一般方法；二、实验仪器信号发生器、交流毫伏表、数字频率计、双踪示波器三、实验原理1、文氏电路如图1所示，电路输出电压和输入电压的幅值分别为Uo 、Ui ，相位分别为φo 、φi ，输出电压和输入电压的比为网络函数，记为H （j ω），网络函数的幅值为∣H （j ω）∣=Uo/Ui ，相位为φ＝φo －φi ，∣H （j ω）∣和φ分别为电路的幅频特性和相频特性。
文氏电路的网络函数表达式为：文氏电路的幅频特性和相频特性见图2和3，在频率较低的情况下，即1/C R ω>>时，电路可近似等效为图4所示的低频等效电路。
频率越低，输出电压的幅度越小，其相位愈超前于输入电压。
当频率接近于0时，输出电压趋近于0，相位接近90度。
而当频率较高时，即当1/C R ω<<时，电路电路可近似等效为图5所示的高频等效电路。
频率越高，输出电压的也幅度越小，其相位愈滞后于输入电压。
当频率接近于无穷大时，输出电压趋近于0，相位接近－90度。
由此可见，当频率为某一中间值o f 时，输出电压不为0，输出电压和输入电压同相。
∣H （j ω）∣ φ图1 RC 文氏电路 图2 文氏电路幅频特性 图3 文氏电路相频特性31arctan)1(31)1(31)(22RC RC RCRC RCRC j UU j H io ωωωωωωω-∠-+=-+==u o+--1/390图4 低频等效电路 图5 高频等效电路2、实验测量框图如图6所示，信号源与RC 网络构成回路，将信号源输出信号和RC 网络端输出信号接入示波器，用频率计测量信号源输出信号的频率。
图6 实验框图 图73、RC 带通网络中心频率0f 的测定当带通网络的频率0f f 时，输入电压和输出电压的相位差为0，如果在示波器的垂直和水平偏转板上分别加上频率、振幅和相位相同的正弦电压，则在示波器的荧光屏上将得到一条与X 轴成45度的直线。
f H≈100KRC电路的低通和高通电路的频率特性1.RC低通电路的频率特性由电阻和电容构成的低通电路如下图：其传递函数为：设则传递函数可以写成：取模化简得其幅频特性为：相频特性为：从其幅频特性曲线如下图，可以看出，当频率f升高时，|Au|逐渐下降，当f=f H时，|Au|=1/√2=0.707，所以我们称f H为低通滤波的上限截止频率，其通频带为0~f H。
因电路只有一个储能元件，所也也称一阶低通滤波电路。
工程上为了作图简便，常用波特图表示，如下图，其中细实线为实际曲线，粗实线为实际曲线的渐近线。
当f≤0.1f H时，近似认为|Au|≈1，即|Au|=(20lg|Au|)dB=0dB当f≥10f H时，近似认为|Au|=1/（f/f H）,也即|Au|≈20lg（f H/f）根据上图可以看出，当f≤0.1f H时，幅频物性的波特图为一条水平线，当f≥10f H时是一条-20dB/十倍频的斜线，两线在f=f H处相交，因此f H也称为转折频率。
在粗略计算时，可以用渐近线代替实际曲线，最大误差发生在f H处，误差为|20lg0.707|dB=20×0.15dB=3dB。
当f≤0.1f H时，相频特性曲线，可以看成φ=0的近似线，当f≥10f H时，近似认为φ=-90，当f=f H时，φ=-45。
在0.1f H<f<10f H区域内，可用一条斜率为-45/十倍频的斜线代替。
其中f=0.1f H和f=10f H误差最大，为5.7度。
2.RC高通电路的频率特性电如如下图：其传递函数为：设由传递函数可写成：取模得其幅频特性：相频特性为：根据其特性可以绘出RC高通电路的波特图其下限截止频率为f L ，通频带为f L ~∞。
为一阶高通滤波。
综合上述的低通和高通滤波电路，它们对信号只有衰减作用，没有放大作用，因些称为无源滤波电路。
上述两种电路常用在有源滤波电路中，在电子分频的音响功放中也比较常见，比如我们可用上述电路，把音响的输入信号二分频后分别进行放大，来代替昂贵的分频器。
实验五 RC 频率特性和RLC 谐振综合实验一、实验目的1、研究RC 串、并联电路及RC 双Ｔ电路的频率特性。
2、学会用交流毫伏表和示波器测定RC 网络的幅频特性和相频特性。
3、熟悉文氏电桥电路的结构特点及选频特性。
4、加深理解电路发生谐振的条件、特点，掌握电路品质因数（电路Q 值）、通频带的物理意义及其测定方法。
5、学习用实验方法绘制R 、L 、C 串联电路不同Q 值下的幅频特性曲线。
二、实验原理1、RC 串并联电路频率特性图5-1所示RC 串、并联电路的频率特性：)1j(31)j (iｏRCRC UU N ωωω-+==其中幅频特性为：22io)1(31)(RCRC U U A ωωω-+==相频特性为：31arctg)(o RC RC i ωωϕϕωϕ--=-=幅频特性和相频特性曲线如图5-2所示，幅频特性呈带通特性。
当角频率RC1=ω时，31)(=ωA ，︒=0)(ωϕu O 与u I 同相，即电路发生谐振，谐振频率RCf π210=。
也就是说，当信号频率为f 0时，RC 串、并联电路的输出电压ｕO 与输入电压u I 同相，其大小是输入电压的三分之一，这一特性称为RC 串、并联电路的选频特性，该电路又称为文氏电桥。
测量频率特性用‘逐点描绘法’，图5-3表明用交流毫伏表和双踪示波器测量RC 网络频率特性的测试图。
测量幅频特性：保持信号源输出电压（即RC 网络输入电压）U I 恒定，改变频率f ，用交流毫伏表监视U I ，并测量对应的RC 网络输出电压U O ，计算出它们的比值A ＝U O ／U I ，图5-1图5-2然后逐点描绘出幅频特性；测量相频特性：保持信号源输出电压（即RC 网络输入电压）U I 恒定，改变频率f ，用交流毫伏表监视U I ，用双踪示波器观察u O 与u I 波形，如图5-4所示，若两个波形的延时为Δt ，周期为T ，则它们的相位差︒⨯∆=360Ttϕ，然后逐点描绘出相频特性。
