热学(秦允豪编)习题解答第四章-热力学第一定律

普通物理学教程《热学》（秦允豪编）习题解答第四章 热力学第一定律4.2.1 解：⎰-=21V V PdVW C T =（1）()RT b v P =-b v RTP -=⎪⎪⎭⎫ ⎝⎛---=--=⎰b v b v dv bv RTW i f v v fi ln（2）⎪⎭⎫ ⎝⎛-=v B RT Pv 1 ⎪⎭⎫ ⎝⎛-=v B RT P 1 ⎪⎪⎭⎫ ⎝⎛-+-=⎪⎭⎫ ⎝⎛--=⎰i f i f v v v v BRT v v RT dv v B RT W f i11ln 14.2.2 应用（4.3）式⎰-=21V V PdVW 且k PiV PV i ==γγ γγ-=V V P P i i故有：fifv v i i V Vii i V V P dV V V P W γγγγγ----=-=⎰111()()i i f f i f i i V P V P V V V P --=--=--111111γγγγγ （应用了γγf f i i V P V P =）4.4.2 （1）2v ab v RT P --=⎰⎰⎰+--=-=dvv adv b v RT Pdv W 2aV V b V b V RT ⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛---=121211ln （2）d v a cT u +-=2当C V =时，V V V dt du dT dQ C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛= ∴C C V =TC CdT Q T T ∆==⎰214.4.3 水蒸气的凝结热即为定压状况下单位质量物质相变时吸收（或释放）的热量，在等压下此值即为比焓变化，即：()kJh mHl V 4.244459.1000.2545-=--=∆-=∆= （系统放热）4.4.4 铜升温过程，是等压过程()212121221T T T T T T P P bT aT dT bT a dT C Q H ⎪⎭⎫⎝⎛+=+===∆⎰⎰()()2122122T T b T T a -+-=()()122447107.2300120092.5213001200103.2-⋅=-⨯⨯+-⨯⨯=mol J4.4.515.46190846823866921291542321223-⋅-=⎪⎭⎫⎝⎛⨯+⨯--=+-=mol J h h h Q H N NH P4.4.6 在定压情况下，21molH 和221molO 化合生成mol 1水时吸收的热量为 1510858.2-⋅⨯-=∆=mol J H Q （系统放热Q Q -='）每产生一个水分子有两个电子自阴极到阳极，生成mol 1水有A N 2电子到阳极。

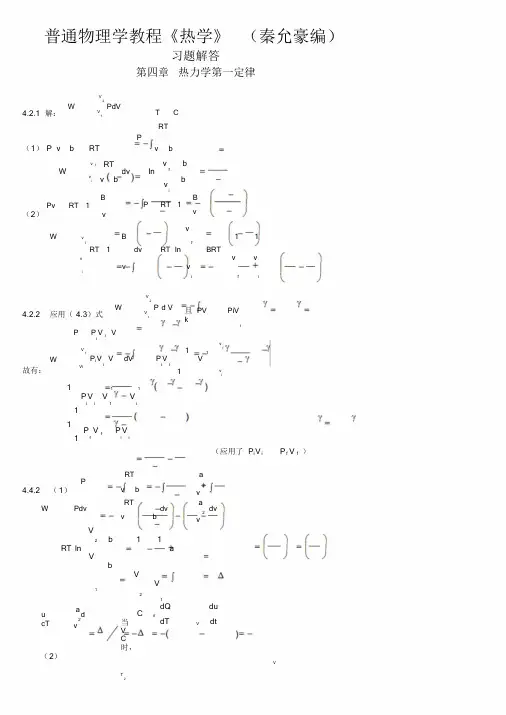
普通物理学教程《热学》 （秦允豪编）习题解答第四章 热力学第一定律V24.2.1 解：WV1PdVT CRT P（1） P v bRT vbWvvi fRT v bdv lnv fvibbB Pv RT 1 （2）vPRT 1B vWvvB11 ffRT 1dv RT lnBRTvvvvviifiV24.2.2 应用（ 4.3）式WV1P d V且PVPiVkiPP V i i V故有：VfWVi1 P i V VdV P VViii11vfvi11 1P V VViifi11 1 P fVfP Vii（应用了 P i V iP f V f ）4.4.2 （1）PRT vba 2vWPdvRT vbdv a 2 vdv V2b 1 1RT lnaVbVV121u cTa 2 vd当VC时，C VdQdT Vdu dt（2）VT2∴C CV QT1C d T C T4.4.3 水蒸气的凝结热即为定压状况下单位质量物质相变时吸收（或释放）的热量，在等压下此值即为比焓变化，即：l HV h 2545 .0 100 .59 2444 .4 m kJ（系统放热）4.4.4 铜升温过程，是等压过程T2H QT T12 2P C dT a bT dT aT bTPT T21 12T1a T2 T1b2T 222T114 2 22.310 1200 300 5. 92 1200 300212. 47107 J mol4.4.5Q hP NH1 3 1 33 h h 29154 8669 8468 46190 .5 J mol2 2N H2 2 2 214.4.6 在定压情况下，1molH 2 和12molO2化合生成1mol 水时吸收的热量为5 1Q （系统放热Q ' Q ）H 2 .858 10 J mol每产生一个水分子有两个电子自阴极到阳极，生成 1 m ol 水有2 N A 电子到阳极。

总电量为q 19 232 （q 2N e ）1 .60 10 6 .02 10 CA两极间电压为， A q19 23A 1 .229 2 1 .60 10 6 .02 1082.84%5Q' 2. 858 104.4.7 设 1 m ol 固体状态方程为：v v aT bP0 ，内能表示为：u CT aPT ，a 均为常数。

热力学第一定律课后习题一、是非题下列各题中的叙述是否正确？正确的在题后括号内画“√”，错误的画“⨯”。

1.在定温定压下，CO2由饱和液体转变为饱和蒸气，因温度不变，CO2的热力学能和焓也不变。

( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。

( )3. 一个系统从始态到终态，只有进行可逆过程才有熵变。

( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。

( )5. 稳定态单质的∆f H(800 K) = 0。

( )二、选择题选择正确答案的编号，填在各题后的括号内：1. 理想气体定温自由膨胀过程为：（）。

（A）Q > 0；（B）∆U < 0；（C）W <0；（D）∆H = 0。

2. 对封闭系统来说，当过程的始态和终态确定后，下列各项中没有确定的值的是：( )。

( A ) Q；( B ) Q＋W；(C ) W( Q = 0 )；( D ) Q( W = 0 )。

3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是：( )(A)绝热过程；( B)理想气体绝热过程；( C )理想气体绝热可逆过程；(D)绝热可逆过程。

4. 在隔离系统内：( )。

( A ) 热力学能守恒，焓守恒；( B ) 热力学能不一定守恒，焓守恒；(C ) 热力学能守恒，焓不一定守恒；( D) 热力学能、焓均不一定守恒。

5. 从同一始态出发，理想气体经可逆与不可逆两种绝热过程：( )。

( A )可以到达同一终态；( B )不可能到达同一终态；( C )可以到达同一终态，但给环境留下不同影响。

6. 当理想气体反抗一定的压力作绝热膨胀时，则：( )。

( A )焓总是不变；(B )热力学能总是增加；( C )焓总是增加；(D )热力学能总是减少。

7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T)，下列说法中不正确的是：（）。

第四章热力学第一定律(题号有所不同)5－1.0.020Kg的氦气温度由升为，若在升温过程中：（1）体积保持不变；（2）压强保持不变；（3）不与外界交换热量，试分别求出气体内能的改变，吸收的热量，外界对气体所作的功，设氦气可看作理想气体，且，解：理想气体内能是温度的单值函数，一过程中气体温度的改变相同，所以内能的改变也相同，为：热量和功因过程而异，分别求之如下：（1）等容过程：V=常量A＝0由热力学第一定律，（2）等压过程：由热力学第一定律，负号表示气体对外作功，（3）绝热过程Q＝0由热力学第一定律5－2.分别通过下列过程把标准状态下的0.014Kg氮气压缩为原体积的一半；（1）等温过程；（2）绝热过程；（3）等压过程，试分别求出在这些过程中气体内能的改变，传递的热量和外界对气体所作的功，设氮气可看作理想气体，且，解：把上述三过程分别表示在P-V图上，（1）等温过程理想气体内能是温度的单值函数，过程中温度不变，故由热一、负号表示系统向外界放热（2）绝热过程由或得由热力学第一定律另外，也可以由及先求得A（3）等压过程，有或而所以＝＝＝由热力学第一定律，也可以由求之另外，由计算结果可见，等压压缩过程，外界作功，系统放热，内能减少，数量关系为，系统放的热等于其内能的减少和外界作的功。

5－3 在标准状态下的0.016Kg的氧气，分别经过下列过程从外界吸收了80cal的热量。

（1）若为等温过程，求终态体积。

（2）若为等容过程，求终态压强。

（3）若为等压过程，求气体内能的变化。

设氧气可看作理想气体，且解：（1）等温过程则故（2）等容过程（3）等压过程5－4 为确定多方过程方程中的指数n，通常取为纵坐标，为横坐标作图。

试讨论在这种图中多方过程曲线的形状，并说明如何确定n。

解：将两边取对数或比较知在本题图中多方过程曲线的形状为一直线，如图所示。

直线的斜率为可由直线的斜率求n。

或即n可由两截距之比求出。

5－5 室温下一定量理想气体氧的体积为，压强为。

热力学第一定律课后习题一、是非题下列各题中的叙述是否正确？正确的在题后括号内画“√”，错误的画“⨯”。

1.在定温定压下，CO2由饱和液体转变为饱和蒸气，因温度不变，CO2的热力学能和焓也不变。

( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。

( )3. 一个系统从始态到终态，只有进行可逆过程才有熵变。

( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。

( )5. 稳定态单质的∆f H(800 K) = 0。

( )二、选择题选择正确答案的编号，填在各题后的括号内：1. 理想气体定温自由膨胀过程为：（）。

（A）Q > 0；（B）∆U < 0；（C）W <0；（D）∆H = 0。

2. 对封闭系统来说，当过程的始态和终态确定后，下列各项中没有确定的值的是：( )。

( A ) Q；( B ) Q＋W；(C ) W( Q = 0 )；( D ) Q( W = 0 )。

3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是：( )(A)绝热过程；( B)理想气体绝热过程；( C )理想气体绝热可逆过程；(D)绝热可逆过程。

4. 在隔离系统内：( )。

( A ) 热力学能守恒，焓守恒；( B ) 热力学能不一定守恒，焓守恒；(C ) 热力学能守恒，焓不一定守恒；( D) 热力学能、焓均不一定守恒。

5. 从同一始态出发，理想气体经可逆与不可逆两种绝热过程：( )。

( A )可以到达同一终态；( B )不可能到达同一终态；( C )可以到达同一终态，但给环境留下不同影响。

6. 当理想气体反抗一定的压力作绝热膨胀时，则：( )。

( A )焓总是不变；(B )热力学能总是增加；( C )焓总是增加；(D )热力学能总是减少。

7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T)，下列说法中不正确的是：（）。

第四章 热力学第一定律 基本要求一、 可逆和不可逆过程 （1）准静态过程（2）理解什么是可逆过程，什么是不可逆过程.知道只有无耗散的准静态过程才是可逆过程。

二、 功和热量 （1）明确功是在力学相互作用过程中能量转移，热量是在热学相互作用过程中的能量的转移，它们都是过程量，它们都是过程量。

知道“作功”是通过物体宏观位移来完成；而“热传递”是通过分子之间的相互作用来完成。

（2）知道功有正负，熟练掌握从体积膨胀功微分表达式pdV W d -=出发计算体积膨胀功。

从几何上理解功的大小等于p-V 图上热力学过程曲线下面的面积。

三、热力学第一定律（1）知道能量守恒与转化定律应用到热学中就是热力学第一定律。

明确热力学第一定律是把内能、功和热量这三个具有能量量纲的物理量结合在一个方程中：即 W Q U +=∆； （2）一微小过程中热力学第一定律表示为：W d Q d dU +=；对于准静态过程热力学第一定律表示为：pdV Q d dU -=（3）内能是态函数，内能一般应是温度和体积的函数。

内能应当包含分子的热运动动能和分子之间的相互作用势能，也应包括分子内部的能量；在热学中的内能一般不包括系统做整体运动的机械能。

四、热容和焓（1）知道热容的定义、热容是过程量、热容与物体的量有关。

（2）知道焓的定义pV U H +=;知道焓的物理意义。

五、热力学第一定律对理想气体的应用（1）知道焦耳定律；即理想气体的内能仅是温度的函数；知道理想气体的焓也只是温度的函数。

内能和焓的微分可分别表示为：dT C dU m V ,ν=；dT C dH m p ,ν=；这两个公式适用于理想气体任何过程。

（2）理想气体的准静态过程的热力学第一定律可表示为pdV dT C dQ m V +=,ν；利用上式可得迈耶公式：R C C m V m p =-,,ν；（3）会熟练利用热力学第一定律处理一些常见热力学过程。

（4）会推导准静态绝热过程方程，熟记并会熟练利用绝热过程方程，同时应知道绝热过程方程的适用条件。

热力学第一定律课后习题一、是非题下列各题中的叙述是否正确？正确的在题后括号内画“√”，错误的画“⨯”。

1.在定温定压下，CO2由饱和液体转变为饱和蒸气，因温度不变，CO2的热力学能和焓也不变。

( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。

( )3. 一个系统从始态到终态，只有进行可逆过程才有熵变。

( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。

( )5. 稳定态单质的∆f H(800 K) = 0。

( )二、选择题选择正确答案的编号，填在各题后的括号内：1. 理想气体定温自由膨胀过程为：（）。

（A）Q > 0；（B）∆U < 0；（C）W <0；（D）∆H = 0。

2. 对封闭系统来说，当过程的始态和终态确定后，下列各项中没有确定的值的是：( )。

( A ) Q；( B ) Q＋W；(C ) W( Q = 0 )；( D ) Q( W = 0 )。

3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是：( )(A)绝热过程；( B)理想气体绝热过程；( C )理想气体绝热可逆过程；(D)绝热可逆过程。

4. 在隔离系统内：( )。

( A ) 热力学能守恒，焓守恒；( B ) 热力学能不一定守恒，焓守恒；(C ) 热力学能守恒，焓不一定守恒；( D) 热力学能、焓均不一定守恒。

5. 从同一始态出发，理想气体经可逆与不可逆两种绝热过程：( )。

( A )可以到达同一终态；( B )不可能到达同一终态；( C )可以到达同一终态，但给环境留下不同影响。

6. 当理想气体反抗一定的压力作绝热膨胀时，则：( )。

( A )焓总是不变；(B )热力学能总是增加；( C )焓总是增加；(D )热力学能总是减少。

7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T)，下列说法中不正确的是：（）。

热力学第一定律习题一、单选题1) 如图，在绝热盛水容器中，浸入电阻丝，通电一段时间，通电后水及电阻丝的温度均略有升高，今以电阻丝为体系有：( )A. W =0，Q <0，U <0B. W <0，Q <0，U >0C. W <0，Q <0，U >0D. W <0，Q =0，U >02) 如图，用隔板将刚性绝热壁容器分成两半，两边充入压力不等的空气(视为理想气体)，已知p右> p左，将隔板抽去后: ( )A. Q＝0, W ＝0, U ＝0B. Q＝0, W <0, U >0C. Q >0, W <0, U >0D. U ＝0, Q＝W03）对于理想气体，下列关系中哪个是不正确的：( )A. (∂U/∂T)V＝0B. (∂U/∂V)T＝0C. (∂H/∂p)T＝0D. (∂U/∂p)T＝04）凡是在孤立孤体系中进行的变化，其U 和H 的值一定是：( )A. U >0, H >0B. U ＝0, H＝0C. U <0, H <0D. U ＝0，H 大于、小于或等于零不能确定。

5）在实际气体的节流膨胀过程中，哪一组描述是正确的: ( )A. Q >0, H＝0, p < 0B. Q＝0, H <0, p >0C. Q＝0, H ＝0, p <0D. Q <0, H ＝0, p <06）如图，叙述不正确的是：( )A.曲线上任一点均表示对应浓度时积分溶解热大小B.H1表示无限稀释积分溶解热C.H2表示两浓度n1和n2之间的积分稀释热D.曲线上任一点的斜率均表示对应浓度时HCl的微分溶解热7）H＝Q p此式适用于哪一个过程: ( )A.理想气体从101325Pa反抗恒定的10132.5Pa膨胀到10132.5sPaB.在0℃、101325Pa下，冰融化成水C.电解CuSO4的水溶液D.气体从(298K，101325Pa)可逆变化到(373K，10132.5Pa )8) 一定量的理想气体，从同一初态分别经历等温可逆膨胀、绝热可逆膨胀到具有相同压力的终态，终态体积分别为V1、V2。

热力学第一定律答案一、选择题1. [ A ]解：真空绝热膨胀过程中0,0==Q A ，由热力学第一定律知0=∆E ，所以0=∆T ，温度不变，对始末二状态，,2211V p V p = V 增大，p 减小。

2. [ C ]解：体积不变时吸热)(221122V p V p i T R iM E Q -=∆⋅=∆=μ，Q 相等，但三种气体的自由度i 不同，故温升T ∆不相同；又p V i Q V V V ∆===2,21, 所以压强的增量也不相同。

3. [ A ]解：由热力学第一定律A E Q +∆=，绝热过程A →D 不吸热，Q = 0等温过程A →C 内能不变，12,0V ACV A Q E AC AC ===∆的面积等压过程A →B ，12,0V ABV E A E Q E AB AB +∆=+∆=>∆面积 所以，AD AC AB Q Q Q >> 吸热最多的过程是A →B 。

4. [ B ] 解：开始时，由RT MpV μ=知，两边V 、T 相等，μ小的p 大，所以22O H p p >。

释放绝热板后H 2膨胀而O 2被压缩，达到新的平衡后，两边压强相等，绝热膨胀后温度降低，绝热压缩温度升高，所以平衡后O 2比H 2温度高。

5. [ B ]解：绝热自由膨胀,0,0==Q A 所以0,0=∆=∆T E 。

以气体为研究对象，,1100V p V p = 因212V V =，所以0121p p =。

6.[ B ]解：功和热量与过程有关，不知是什么过程，无法求；由RT MpV μ=，μ不知道无法求质量M ；内能的变化(),221122V p V p i T R iM E -=∆=∆μ因i = 3，2121V V p p 、、、已知，故可求。

二、填空题1. 体积、温度和压强； 分子的运动速度、动量和动能 。

122. (1) 外界传给系统的热量 等于 零； (2) 外界对系统作的功 大于 零； (3) 系统的内能的增量 大于 零。

热学思考题和参考解答第一章 热学基础知识和温度1．1 若热力学系统处于非平衡态，温度概念能否适用？【答】 对于处于非平衡态的系统，只要局域平衡条件能满足，则对于处于局域平衡的每个子系统来说，温度概念仍能适用。

1．2 系统A 和B 原来各自处在平衡态，现使它们互相接触，试问在下列情况下，两系统接触部分是绝热的还是透热的，或两者都可能?(1)当A V 保持不变，A p 增大时，B V 和B p 都不发生变化；(2)当A V 保持不变，A p 增大时，B p 不变而B V 增大；(3)当A V 减少，A p 增大时，B V 和B p 均不变．【答】设容器都是密闭的．(1)是绝热的．因为A p A V 增大，所以A 的温度 增加．但它并不使B 状态发生变化，说明既没有热量传递也没有做功．(2)是透热的．因为A p A V 增大，所以A 的温度增加．从B 来说，B V 增加了，说明B 膨胀对外做了功，其能量只能来源于从A 吸热．(3)因为B V 和B p 均不变，说明B 的温度不变．但是A V 减少，同时A p 增大，这两者的乘积可变可不变，所以A 的温度也可变可不变．若A 的温度改变则是绝热的；若A 的温度不变，则A ，B 相互 接触的部分仍然绝热，因为B 的状态始终不变．1．3 在建立温标时是否必须规定热的物体具有较高的温度，冷的物体具有较低的温度?是否可作相反的规定?在建立温标时，是否须规定测温属性一定随温度作线性变化?【答】 在建立温标时必须规定热的物体具有较高的温度，冷的物体具有较低的温度，因为热量是从高温物体传递到低温物体的．很有意思的是，对于处于负温度的子系则是例外．因为负温度比正温度还要高，热量是从负温度物体流向正温度物体的．建立温标时并不一定规定测温属性随温度作线性变化，这完全由分度公式来规定．1．4 冰的正常溶点是多少？纯水的三相点温度是多少？【答】 冰的正常溶点是273.15K,纯水的三相点温度是273.16K 。

习题分析和解答[说明：本栏内容对学生是有条件地开放]第一章△1. 3. 6一抽气机转速1m in 400-⋅=r ω，抽气机每分钟能抽出气体20 l (升)。

设容器的容积 V 0 = 2.0 1，问经过多长时间后才能使容器内的压强由0.101 Mpa 降为 133 Pa 。

设抽气过程中温度始终不变。

〖分析〗： 抽气机每打开一次活门, 容器内气体的容积在等温条件下扩大了 V , 因而压强有所降低。

活门关上以后容器内气体的容积仍然为 V 0 。

下一次又如此变化，从而建立递推关系。

〖解〗： 抽气机抽气体时，由玻意耳定律得：活塞运动第一次：)(0100V V p V p +=0001p V V V p +=活塞运动第二次： )(0201V V p V p +=02001002p V V V p V V V p ⎪⎪⎭⎫ ⎝⎛+=+= 活塞运动第n 次： )(001V V p V p n n +=- n n V V V p p ⎪⎪⎭⎫ ⎝⎛+= 000 V V V n p p n n +=00ln（1） 抽气机每次抽出气体体积 l 05.0l )400/20(==V l 0.20=V Pa 1001.150⨯=p Pa 133=n p将上述数据代入（1）式，可解得 276=n 。

则 s 40s 60)400/276(=⨯=t1. 3. 8 两个贮着空气的容器 A 和 B ，以备有活塞之细管相连接。

容器A浸入温度为 C 10001=t 的水槽中，容器B 浸入温度为C 2002-=t 的冷却剂中。

开始时，两容器被细管中之活塞分隔开，这时容器 A 及 B 中空气的压强分别为 MPa 3053.01=p ，MPa 0020.02=p 。

它们的体积分别为 ,l 25.01=V l,40.02=V 试问把活塞打开后气体的压强是多少？〖分析〗： 把活塞打开后两容器中气体混合而达到新的力学平衡以后，A 和 B 中气体压强应该相等。