第一章热力学第一定律
- 格式:doc
- 大小:3.74 MB
- 文档页数:27



热力学第一定律一、基本概念1.系统与环境敞开系统:与环境既有能量交换又有物质交换的系统。
封闭系统:与环境只有能量交换而无物质交换的系统。
(经典热力学主要研究的系统)孤立系统:不能以任何方式与环境发生相互作用的系统。
2.状态函数:用于宏观描述热力学系统的宏观参量,例如物质的量n、温度T、压强p、体积V等。
根据状态函数的特点,我们把状态函数分成:广度性质和强度性质两大类。
广度性质:广度性质的值与系统中所含物质的量成正比,如体积、质量、熵、热容等,这种性质的函数具有加和性,是数学函数中的一次函数,即物质的量扩大a倍,则相应的广度函数便扩大a倍。
强度性质:强度性质的值只与系统自身的特点有关,与物质的量无关,如温度,压力,密度,摩尔体积等。
注:状态函数仅取决于系统所处的平衡状态,而与此状态的历史过程无关,一旦系统的状态确定,其所有的状态函数便都有唯一确定的值。
二、热力学第一定律热力学第一定律的数学表达式:对于一个微小的变化状态为:dU=公式说明:dU表示微小过程的内能变化,而δQ和δW则分别为微小过程的热和功。
它们之所以采用不同的符号,是为了区别dU是全微分,而δQ和δW不是微分。
或者说dU与过程无关而δQ和δW却与过程有关。
这里的W既包括体积功也包括非体积功。
以上两个式子便是热力学第一定律的数学表达式。
它们只能适用在非敞开系统,因为敞开系统与环境可以交换物质,物质的进出和外出必然会伴随着能量的增减,我们说热和功是能量的两种传递形式,显然这种说法对于敞开系统没有意义。
三、体积功的计算1.如果系统与环境之间有界面,系统的体积变化时,便克服外力做功。
将一定量的气体装入一个带有理想活塞的容器中,活塞上部施加外压。
当气体膨胀微小体积为dV时,活塞便向上移动微小距离dl,此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积因为我们假设活塞没有质量和摩擦,所以此活塞实际上只代表系统与环境之间可以自由移动的界面。
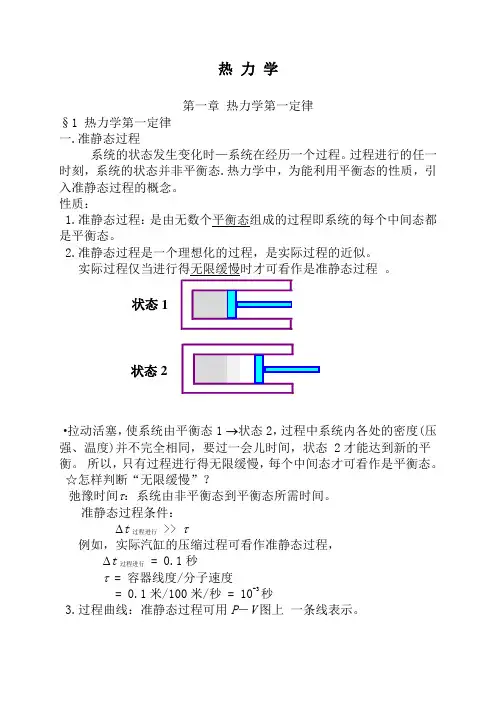
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。
过程进行的任一时刻,系统的状态并非平衡态.热力学中,为能利用平衡态的性质,引入准静态过程的概念。
性质:1.准静态过程:是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。
2.准静态过程是一个理想化的过程,是实际过程的近似。
实际过程仅当进行得无限缓慢时才可看作是准静态过程 。
·拉动活塞,使系统由平衡态1 →状态2,过程中系统内各处的密度(压强、温度)并不完全相同,要过一会儿时间,状态 2才能达到新的平衡。
所以,只有过程进行得无限缓慢,每个中间态才可看作是平衡态。
☆怎样判断“无限缓慢”?弛豫时间τ:系统由非平衡态到平衡态所需时间。
准静态过程条件: ∆t 过程进行 >> τ例如,实际汽缸的压缩过程可看作准静态过程, ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线:准静态过程可用P -V 图上 一条线表示。
状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。
·机械功(摩擦功、体积功)2.内能·内能包含系统内:(1)分子热运动的能量;(2)分子间势能和分子内的势能;(3)分子内部、原子内部运动的能量; (4)电场能、磁场能等。
·内能是状态的函数*对于一定质量的某种气体,内能一般是T 、V 或P 的函数; *对于理想气体,内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i :自由度; ν :摩尔数 ·通过作功改变系统内能的实质是:分子的有规则运动能量和分子的无规则运动能量的转化和传递。
3.热量·传热也可改变系统的状态,其条件是系统和外界的温度不同。
·传热的微观本质:是分子的无规则运动能量从高温物体向低温物体传递。




第一章 热力学第一定律核心内容:能量守恒 ΔU=Q+W主要内容:三种过程(单纯pVT 变化、相变、化学反应)W 、Q 、ΔU 、ΔH 的计算一、内容提要1.热力学第一定律与状态函数(1)热力学第一定律: ΔU=Q+W (封闭系统) 用途:可由ΔU ,Q 和W 中的任意两个量求第三个量。
(2)关于状态函数(M )状态函数:p 、V 、T 、U 、H 、S 、A 、G ……的共性: ①系统的状态一定,所有状态函数都有定值;②系统的状态函数变化值只与始终态有关,而与变化的途径无关。
用途:在计算一定始终态间的某状态函数增量时,为了简化问题,可以撇开实际的复杂过程,设计简单的或利用已知数据较多的过程进行计算。
ΔM (实)=ΔM (设)。
这种方法称为热力学的状态函数法。
③对于循环过程,系统的状态函数变化值等于零,即ΔM =0。
此外,对于状态函数还有如下关系:对于组成不变的单相封闭系统,任一状态函数M 都是其他任意两个独立自变量(状态函数)x 、y 的单值函数,表示为M=M(x 、y),则注意:因为W 和Q 为途径函数,所以Q 和W 的计算必须依照实际过程进行。
⎰-=21V V a m bdV p W ,其中p amb 为环境压力。
Q 由热容计算或由热力学第一定律求得。
dy y M dx x M dM xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂=)(1循环关系式-=⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂xM y M y y x x M )(22尤拉关系式xy My x M ∂∂∂=∂∂∂1(p 1,V 1,T 1) (p'1,V 1,T 2) 2(p 2,V 2,T 2) (p 1,V'1,T 2) VT 将热力学第一定律应用于恒容或恒压过程,在非体积功为零(即w'=0)的情况下有:Q V =ΔU ,Q p =ΔH (H 的定义:H=U+pV )。
此时,计算Q v 、Q p 转化为计算ΔU 、ΔH ,由于U 、H 的状态函数性质,可以利用上面提到的状态函数法进行计算。


引言:1.热力学是研究热与其他能量之间的转化规律;2.化学热力学——热力学在化学中的应用;②化学变化的方向和限度——热力学第二定律特点:①宏观性质——研究系统宏观性质,而不考虑微观结构和微观因素②只考虑系统的始末态,而不追究过程的细节和速率局限性:只能对现象之间的联系做宏观的了解,而不能作微观的说明或给出宏观性质的数值。
§1.1 基本概念一、系统和环境㈠定义系统:研究对象,包括物质,空间环境:与系统紧密相关的外界㈡系统分类①敞开系统:系统与环境有物质和能量的交换②封闭系统;系统与环境无物质交换,有能量交换③隔离系统: 系统与环境无物质和能量的交换二、状态与状态函数※1.状态:系统趋于某一确定的热力学平衡态(力平衡、热平衡、化学平衡、相平衡)状态函数:描述状态的宏观物理学量(宏观量:温度T、体积V、压强P、熵S、焓H……)☆☆☆注意:⑴状态一定,状态函数一定;状态函数一定,状态一定(单一值)。
⑵只要有一个状态函数改变,状态就改变。
⑶状态的确定:ⅰ.单组分密闭均相系统,只要指定两个状态函数,状态就一定,而其他的状态函数Z将随之而定,因为Z=F(T,P).ⅱ.K种物质的多组分系统,指定T、P、X1、X2、X3...Xk-1,状态一定,Z=F(T、P、X1、X2、X3...Xk-1)(K个组分的浓度要一一指定).2.状态函数的特点:⑴状态一定,状态函数值一定。
⑵状态函数的改变量只取决于始末态,与途径无关△Z=∫dZ=Z末-Z初⑶系统循环一周,状态改变量为零,△Z=∮dZ=0.3.状态函数的全微分性Z=F(T、P)微小变化dZ=(dZ/dT)p dT+(dZ/dP)T dP4.状态函数的分类是否具有加和性:⑴广度性质——v、n、H、S...与物质的量有关,具有加和性⑵强度性质——T、P、M...自身特性,不具加和性两个广度性质之比=强度性质如,V m=V/n,C=n/V.三、过程和途径过程:任何状态的改变①等温过程:T初=T末=T环=常数②等压过程:P初=P末=P外=常数●恒外压过程:P初≠P末=P外=常数③等容过程:体积不变,△V=0.④绝热过程:系统与环境无热交换(爆炸瞬间)⑤循环过程:初态经过某个过程又回到初态,△Z=0.途径:初态到达末态具体的步骤.四、功和热※1.定义:热(Q)——系统与环境间由于温差所传递的能量功(W)——除热以外的其他所能传递的能量2.系统吸热Q为正,Q>0;放热Q为负,Q<0.系统对环境做功W为负,W<0;环境对系统做功,W为正,W >0.3.功和热不是状态函数,其值与途径有关.4.功的分类:其他功Wf(电功、表面功…)体积功dW=-P外dV W=∫- P外dV=-P外(V2-V1)5.功的计算方法①等容过程:△V=0或dV=0,W=∫- P外dV=0.②自由膨胀:P外=0,W=∫- P外dV=0.③恒外压过程:P外=常数,W=∫- P外dV=-P外(V2-V1).④等压过程:P1=P2=P外=常数,W=∫- P外dV=-P外(V2-V1). 例1:1mol理想气体由27℃、101.325Kpa在外压恒定为831400Pa下压缩到27℃,0.003m3,求压缩功。
第一章热力学第一定律本章主要内容1.1热力学概论1.2热力学第一定律1.3 可逆过程和最大功1.4 焓1.5 热容1.6 热力学第一定律对理想气体的应用1.7实际气体1.8热化学1.9化学反应热效应的求算方法1.10反应热与温度的关系——基尔霍夫定律§1.1热力学概论1.1.1热力学的研究对象(1)研究热、功和其他形式能量之间的相互转换及其转换过程中所遵循的规律;(2)研究各种物理变化和化学变化过程中所发生的能量效应;(3)研究化学变化的方向和限度。
1.1.2 热力学的方法和局限性热力学方法:热力学在解决问题是使用严格的数理逻辑推理方法,其研究对象是大量质点的集合体,所观察的是宏观系统的平均行为,并不考虑个别分子或质点,所得结论具有统计意义。
优点:只须知道宏观系统变化的始终态及外部条件,无须知道物质的微观结构和变化的细节即可进行有关的定量计算。
局限性:(1)对所得的结论只知其然而不知所以然;(2)不能给出变化的实际过程,没有时间的概念,也不能推测实际进行的可能性。
(3)只能适应用于人们所了解的物质世界,而不能任意推广到整个宇宙。
1.1.3 几个基本概念:1、系统与环境系统(System)——把一部分物质与其余分开作为研究对象,这这种被划定的研究对象称为系统,亦称为物系或系统。
环境(surroundings)——与系统密切相关、有相互作用或影响所能及的部分称为环境。
(1)敞开系统(open system) -系统与环境之间既有物质交换,又有能量交换。
(2)封闭系统(closed system)-系统与环境之间无物质交换,但有能量交换。
(3)孤立系统(isolated system )-系统与环境之间既无物质交换,又无能量交换,故又称为隔离系统。
有时把封闭系统和系统影响所及的环境一起作为孤立系统来考虑。
2、状态与状态性质(1)热力学系统的所有物理性质和化学性质的综合表现称为状态,而描述状态的的性质被称为状态性质(或热力学性质)一般用宏观可测性质来描述系统的热力学状态,故这些性质又称为热力学变量。
可分为两类:● 广度性质(extensive properties )又称为容量性质,其数值与系统的物质的量成正比,如体积V 、质量m 等。
这种性质有加和性。
● 强度性质(intensive properties )数值取决于系统自身的特点,与系统的数量无关,不具有加和性。
如温度、压力等。
容量性质与物质的量之比为强度性质,如摩尔体积n VV m 。
(2)状态函数系统的一些性质,其数值仅取决于系统所处的状态,而与系统的历史无关;其变化值仅取决于系统的始态和终态,而与变化的途径无关。
具有这种特性的物理量称为状态函数(state function )。
状态函数的特性可描述为:异途同归,值变相等;周而复始,数值还原。
状态函数在数学上具有全微分的性质。
(举P 、V 、T 关系的例子) 3、热力学平衡态当系统的诸性质不随时间而改变,则系统就处于热力学平衡态。
它包括下列几个平衡:● 热平衡(thermal equilibrium ) 系统各部分温度相等。
● 力平衡(mechanical equilibrium )系统各部分的压力都相等,边界不再移动。
如有刚壁存在,虽双方压力不等,但也能保持力学平衡。
●相平衡(phase equilibrium)多相共存时,各相的组成和数量不随时间而改变。
●化学平衡(chemical equilibrium )反应系统中各物质的量不再随时间而改变。
4、过程与途径过程——系统所发生的一个变化途径——变化的具体形式●几个特殊过程:(1)恒压过程——P1=P2=P外(2)恒容过程——V1 = V2(3)恒温过程——T1 = T2 = T源(4)恒温恒压——T1 = T2 = T源P1=P2=P外(5)恒温恒容——T1 = T2 = T源P1=P2=P外(6)恒外压过程——P≡常数= P2外(7)绝热过程——系统与环境无热交换§1.2 热力学第一定律1.2.1能量守恒与转化定律能量守恒与转化定律可表述为:自然界的一切物质都具有能量,能量有各种不同形式,能够从一种形式转化为另一种形式,但在转化过程中,能量的总值不变。
1.2.2 热力学能(thermodynamic energy )热力学能也称为内能(internal energy ),它是指系统内部能量的总和,包括分子运动的平动能、分子内的转动能、振动能、电子能、核能以及各种粒子之间的相互作用位能等。
热力学能是状态函数,用符号U 表示,其绝对值无法测定,只能求出它的变化值。
U = Et + Er + Ev + Ee + En + Ej全微分表达式(对无相变、无化学变化的定组成系统))21()()(),()11()()(),(-∂∂+∂∂=⇒=-∂∂+∂∂=⇒=dPP UdT T U dU P T f U dV V U dT T U dU V T f U T P T V1.2.3 热和功 ● 热(heat )系统与环境之间因温差而传递的能量称为热,用符号Q 表示。
Q 的取号为: 系统吸热,Q >0; 系统放热,Q <0 。
热分为显热、潜热和化学反应热等。
● 功(work )系统与环境之间传递的除热以外的其它能量都称为功,用符号W 表示。
W 的取号为:环境对系统作功,W > 0; 系统对环境作功,W <0 。
功可分为膨胀功(既体积功)和非膨胀功两大类。
● Q 和W 都不是状态函数,其数值与变化途径有关。
● 功和热的实质热—分子的无序运动结果; 功—分子的有序运动结果1.2.4 热力学第一定律经典描述1、经典描述一种既不靠外界提供能量,本身也不减少能量,却可以不断对外作功的机器称为第一类永动机,而第一类永动机是不可能制成的。
2、说明热力学第一定律是人类经验的总结,是能量守恒与转化定律在热现象领域内所具有的特殊形式。
3、第一定律的数学表达式对有限变化∆U = Q + W (1-3)对微小变化: d U = δQ +δW (1-4)说明:因为热力学能是状态函数,数学上具有全微分性质,微小变化可用d U表示;Q和W不是状态函数,微小变化用δ表示,以示区别。
(数学表达式的另一种形式:∆U = Q - W ,此种情况下,功值取号与前面相反。
)[例题1]设有一电炉丝浸于水中,接上电源,通电一段时间后,按下列几种情况作为系统,试问ΔU、Q、W是为正、为负还是为零?(1)以电炉丝为系统;(2)以电炉丝和水为系统;(3)以电炉丝、水、电源及其他所有部分为系统。
解:(1)ΔU>0;Q<0;W>0(2)ΔU>0;Q=0;W>0(3)ΔU=0;Q=0;W=0 [例题2]1系统沿途径1→a→2,Q=314.0J,W= -117.0J(如右图所示)。
试问:(1)当系统沿1→b →2变化时,W=- 44J ,Q 值为多少? (2)若系统沿C 途径由2→1,W=79.5J ,则Q 值为多少? 解:(1)ΔU 1→2 = Q+W = 314.0 - 117.0 = 197.0J Q =ΔU -W = 197.0 +44 = 241.0J (2)ΔU 2→1 = - ΔU 1→2 = - 197.0JQ = ΔU -W = - 197.0 - 79.5 = - 276.0J§1.3 准静态过程与可逆过程1.2.1 体积功 定义:系统反抗外压发生体积变化时与环境交换的功称作体积功,也叫膨胀功。
计算式:设一系统变化如图。
当活塞 移动dl 时,系统体积增加dv ,系统 对外作功为:)51(--=-=-=dV p Adl p dl f W e e e δ有限变化时:dVP W W V V e ⎰-=∑=21δ (1-6)1.3.2 功与过程—几个特殊过程的体积功设在定温下,一定量理想气体在活塞筒中克服外压 ,经4种不同途径,体积从V 1膨胀到V 2所作的功分别为:1、自由膨胀(free expansion )0211,=-=⎰dV P WV e e(1-7) 2、恒温一次等外压膨胀(p e 保持不变)V p V V p dV p W V V e e ∆-=--=-=⎰21222,)(21(1-8)−−→−=0e p −−→−=2p p e3、恒温二次等外压膨胀所作的功等于2次作功的加和:2,122'221'2'221''3,)()()()()(e e W V V p V V p V V p V V p V V p W =--=---〈-----= (1-9)4.恒温下外压比内压小一个无穷小的值这样的膨胀过程是无限缓慢的,每一步都接近于平衡态。
所作的功为:(气体作为理想气体)124,ln )(21212121V V nRT dV V nRTdVp dV dp p dV p W V V V V V V V V e e -=-=-=--=-=⎰⎰⎰⎰ (1-10)三种不同形式的膨胀做功绝对值大小如图中阴影面积:显然,|W e ,2 |<| W e ,3|< |W e ,4| ,说明始终态相同而途径不同时,系统所做的功不同,无限缓慢膨胀做功最大。
若用同样的三种方式压缩系统使回到原状,则需环境作功的情况如下: )(121'2,V V p W e -=)()()(1211'1'2''3,V V p V V p V V p W e -〈-+-= )/ln(12'4,V V nRT W e =−−→−=,p pe −−→−=,p pe−−−−-=dpp pe 阴影部分为|W|阴影部分为|W|阴影部分为|W|图中阴影部分面积等于环境对系统所做的功。
由图可以看出: W e ,4 ’< W e ,3’<W e ,2’,而 W e ,4 ’= |W e ,4| ,所以,无限缓慢膨胀,系统对环境作最大功;无限缓慢压缩,环境对系统作最小功。
1.3.2、可逆过程(reversible process ) 1、准静态过程(guasistatic process )在过程进行的每一瞬间,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
准静态过程是一种理想过程,实际上不可能实现。
上例无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
2、可逆过程系统经过某一过程从状态(1)变到状态(2)之后,如果能使系统和环境都恢复到原来的状态而未留下任何永久性的变化,则该过程称为热力学可逆过程。
否则为不可逆过程。