第一章 热力学第一定律

系统在环境温度不变的条件下发生的变化历程。T1=T2=Te
2). 恒压过程(isobaric process)： 系统在环境压力不变的条件下发生的变化历程。P1=P2=Pe
3) .恒容过程(isochoric process)：
容积不变的系统发生的变化历程。V1=V2
4) 绝热过程(adiabatic process)： 系统在与环境间无热量交换的条件下发生的变化历程。 5) 循环过程(cyclic process)：
化学热力学是怎样产生的？
19世纪，发明蒸汽机，导致工业革命的出现。
蒸汽机：燃煤锅炉——产生高温高压水蒸气——推动机械运转 “热能——机械能” 如何提高“热 — 机”效率？
总结并发现热力学一、二定律——热力学的主要基础。
第一定律：研究化学变化过程中的热效应等能量转换问题。 第二定律：研究化学变化过程的方向和限度。
定义 H=U+PV (焓) QP =H2－H1=△H
对微小的恒压过程， δQP= dH
由于H=U+PV，所以焓是状态函数。△H=△U+△(PV) 热力学定义焓的目的，主要在于研究问题的方便。 物理意义：对于只作膨胀功的恒压过程，系统焓的变化在数值 上等于过程的热。
因恒压热等于系统的焓变，故恒压热也只决定于系统的初末态，与过程无关。
宏观性质统称为状态函数(state function)。
2. 状态函数： 状态函数是系统所处状态的单值函数。对于确定的状态，所 有的状态函数都有确定的值。相反，当状态函数发生变化时， 状态也随之变化。 ★状态和性质之间是相互影响，相互制约的，系统的状态性质 中只要有一个发生变化，必将引起其它性质的变化。 因此，描述系统的状态时，并不需要罗列系统的全部性质。 例：理想气体状态方程

pdV pvdm
对于单位质量工质，
wf pv
流动功是由泵或风机加给被输送工质并随 工质流动向前传递的一种能量，非工质本身具 有的能量。
40
二、开口系统的稳定流动能量方程 在 时间内,
进口质量 m1、 流 速 cf1、 标 高 z1
出口质量 m2、 流 速 cf2、 标 高 z2
稳定流动：
34
（2）示热图 在可逆过程中 单位质量工质与外 界交换的热量可以 用T-s 图（温熵图） 上过程曲线下的面 积来表示。 温熵图也称 示热图
q Tds
1 2
例1-5
35
§1-5
热力学第一定律及其解析式
一、热力学第一定律的实质
热力学第一定律实质就是热力过程中的 能量守恒和转换定律 ，可表述为 ：
W pAdx pdV
对于可逆过程1～2： W

2 1
pdV
30
单位质量工质所作的膨胀功用符号w 表 示，单位为J/kg 或 kJ/kg。
w pdv
膨胀：dv > 0 , w > 0 压缩：dv < 0 , w < 0 (2) 示功图（p-v图） w的大小可以 pv 图上的过程曲线下 面的面积来表示 。 功是过程量而不 是状态量。
w pdv
1
2
31
二、热量与示热图
（1）热量 系统与外界之间依靠温差传递的能量称 为热量。符号：Q ；单位：J 或kJ。 单位质量工质所传递的热量用q 表示，单 位为 J/kg 或 kJ/kg。 热量正负的规定： 系统吸热：q > 0 ; 系统放热：q < 0 。 热量和功量都是系统与外界在相互作用的过 程中所传递的能量，都是过程量而不是状态量

热力学第一定律一、基本概念1.系统与环境敞开系统：与环境既有能量交换又有物质交换的系统。

封闭系统：与环境只有能量交换而无物质交换的系统。

（经典热力学主要研究的系统）孤立系统：不能以任何方式与环境发生相互作用的系统。

2.状态函数：用于宏观描述热力学系统的宏观参量，例如物质的量n、温度T、压强p、体积V等。

根据状态函数的特点，我们把状态函数分成：广度性质和强度性质两大类。

广度性质：广度性质的值与系统中所含物质的量成正比，如体积、质量、熵、热容等，这种性质的函数具有加和性，是数学函数中的一次函数，即物质的量扩大a倍，则相应的广度函数便扩大a倍。

强度性质：强度性质的值只与系统自身的特点有关，与物质的量无关，如温度，压力，密度，摩尔体积等。

注：状态函数仅取决于系统所处的平衡状态，而与此状态的历史过程无关，一旦系统的状态确定，其所有的状态函数便都有唯一确定的值。

二、热力学第一定律热力学第一定律的数学表达式：对于一个微小的变化状态为：dU=公式说明：dU表示微小过程的内能变化，而δQ和δW则分别为微小过程的热和功。

它们之所以采用不同的符号，是为了区别dU是全微分，而δQ和δW不是微分。

或者说dU与过程无关而δQ和δW却与过程有关。

这里的W既包括体积功也包括非体积功。

以上两个式子便是热力学第一定律的数学表达式。

它们只能适用在非敞开系统，因为敞开系统与环境可以交换物质，物质的进出和外出必然会伴随着能量的增减，我们说热和功是能量的两种传递形式，显然这种说法对于敞开系统没有意义。

三、体积功的计算1.如果系统与环境之间有界面，系统的体积变化时，便克服外力做功。

将一定量的气体装入一个带有理想活塞的容器中，活塞上部施加外压。

当气体膨胀微小体积为dV时，活塞便向上移动微小距离dl，此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积因为我们假设活塞没有质量和摩擦，所以此活塞实际上只代表系统与环境之间可以自由移动的界面。

例1-1 在恒定外压 在恒定外压pex=500kPa条件下，将n=2 条件下， 条件下 mol理想气体，从始态 1=300K、p1=500kPa加 理想气体， 理想气体 从始态T 、 加 热到T 过程的体积功。 热到 2=350K、p2=500kPa。求：过程的体积功。 、 。
解：先求出两种状态下的始态和终态体积。再由恒压 先求出两种状态下的始态和终态体积。 体积功的计算方法计算体积功。 体积功的计算方法计算体积功。
V1=nRT1/p1=[2*8.314*300/(500*1000)]m3= 9.977*10-3m3 V2=nRT2/p2=[2*8.314*350/(500*1000)]m3= 1.164*10-2m3 恒压既p1=p2=pex W = -pex（V2-V1） = -[500*1000*(1.164*10-2-9.977*10-3)] = -832J
热量的符号： 热量的符号：Q 体系从环境吸热为Q>0，“+” 体系从环境吸热为 ， 体系向环境放热为Q<0，“-” 体系向环境放热为 ， 体系绝热，Q=0 体系绝热， 单位：国际单位（ ）， 焦耳（ ）， ），KJ 单位：国际单位（SI）， 焦耳（J），
热容：一定量物质，温度升高 所吸收的 热容：一定量物质，温度升高1K所吸收的 热。 常用符号为C 常用符号为 摩尔热容：1mol物质的热容。 物质的热容。 摩尔热容： 物质的热容 表示符号为C 单位为J.mol-1.K-1 表示符号为 m，单位为 说明：热容为容量性质，随物质的量变化。 说明：热容为容量性质，随物质的量变化。 摩尔热容为强度性质， 摩尔热容为强度性质，其数值与温度 T有关。 有关。 有关
始态 终态 ——→ （ n，T1， P1， V1）——→ （n，T2， P2， V2） ， ， 途径 I 等T 等P （ n，T1， P2， V`2） ， 途径 II

第一章 热力学第一定律
3.热力学能 热力学能：系统内部 能量的总和。符号U ，单位J 。它由多部 分组成： 分子的平动能、转动能、振动能、电子能、 原子核能及分子间 相互作用的势能。
一定量物质在确定状态，热力学能值为确定。但其绝对值是不 知道的。（如果对于某特定物质给予一个基准态，设该态 U=0，则可求得其它态的相对值）
系统分为：封闭系统、隔离系统和敞开系统。
隔离系统的例： 一个完好的热水 瓶：既不传热,也 无体积功与非体 积功的交换,且无 物质交换.
封闭系统的例： 一个不保温的热 水瓶：传热但无 物质交换；一个 汽缸:有功的交换, 但无物质交换.
敞开系统的例 ：一个打开塞 子的热水瓶： 既有能量交换 ，又有物质交 换。
2
1.1 热力学概论
热力学的研究对象 热力学的方法和局限性 几个基本概念：（复习） •系统与环境
•系统的性质 •热力学平衡态
•状态函数
•状态方程
•过程和途径
1 热力学的研究对象 •研究热、功和其他形式能量之间的相互转换及
其转换过程中所遵循的规律。具体：
研究基础：热力学第一、二定律--人类长期 实践经验的总结。 研究内容： •研究各种物理变化和化学变化过程中所发生的 能量效应--热力学第一定律；
V=f（p,T）
例如，理想气体的状态方程可表示为：
pV=nRT
第一章 热力学第一定律—热力学基本概念
(2) 广度量和强度量
描述热力学系统的性质ቤተ መጻሕፍቲ ባይዱ为： 广度量（或广度性质）：与物质的数量成正比的性质。如V，Cp ，
U，„等。它具有加和性。
强度量（或强度性质）：与物质的数量无关的性质，如 p、Ｔ和组 成等。它不具有加和性。 两者的关系： 广度量与广度量的比是强度性质，例如，定压热容，Cp，为 广度量，物质的量n为广度量，摩尔定压热容Cp , m为强度量。

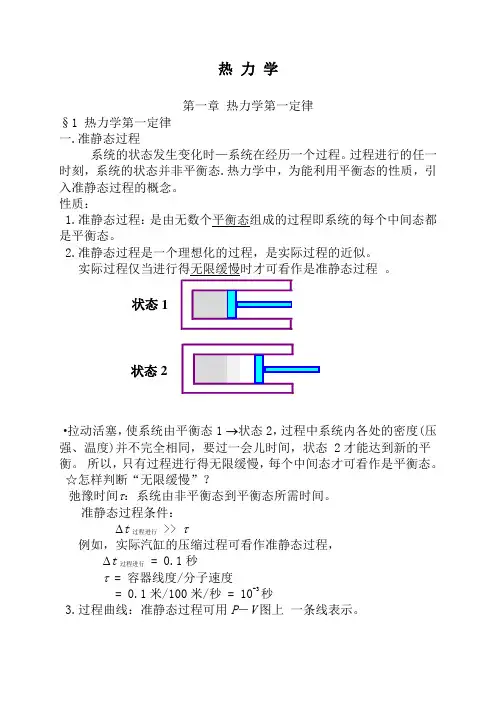
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。

过程进行的任一时刻，系统的状态并非平衡态.热力学中，为能利用平衡态的性质，引入准静态过程的概念。

性质：1.准静态过程：是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。

2.准静态过程是一个理想化的过程，是实际过程的近似。

实际过程仅当进行得无限缓慢时才可看作是准静态过程 。

·拉动活塞，使系统由平衡态1 →状态2，过程中系统内各处的密度(压强、温度)并不完全相同，要过一会儿时间，状态 2才能达到新的平衡。

所以，只有过程进行得无限缓慢，每个中间态才可看作是平衡态。

☆怎样判断“无限缓慢”？弛豫时间τ：系统由非平衡态到平衡态所需时间。

准静态过程条件： ∆t 过程进行 >> τ例如，实际汽缸的压缩过程可看作准静态过程， ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线：准静态过程可用P －V 图上 一条线表示。

状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。

·机械功(摩擦功、体积功)2.内能·内能包含系统内：(1)分子热运动的能量；(2)分子间势能和分子内的势能；(3)分子内部、原子内部运动的能量； (4)电场能、磁场能等。

·内能是状态的函数*对于一定质量的某种气体，内能一般是T 、V 或P 的函数； *对于理想气体，内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i ：自由度； ν ：摩尔数 ·通过作功改变系统内能的实质是：分子的有规则运动能量和分子的无规则运动能量的转化和传递。

3.热量·传热也可改变系统的状态，其条件是系统和外界的温度不同。

·传热的微观本质：是分子的无规则运动能量从高温物体向低温物体传递。

示，其微小量用dU表示。 说明： 1、U是状态函数，广度性质，数学上具有全微分。 若是 组成一定的单相封闭系统，经验证明，用 p，V，T 中的任意两个就能确定系统的状态， 即
U U U (T , p ) ； U ( T , V )
； U
U ( p ,V )
如果是 U U (T , p ) 全微分式： d U
0
六、热和功
1、热（heat） 系统与环境之间因温差而传递的能量称热， 从微观上看，热是体系分子无序热运动的能量交 换。用符号Q 表示，其微小量用 Q 表示。 Q的取号：系统吸热，Q>0 系统放热，Q<0
计算Q一定要与系统与环境之间发生热交换 的过程联系在一起，系统内部的能量交换不可能 是热。 热分类：显热、潜热（恒温恒压的相变过程）、 化学热。
3、相平衡（phase equilibrium） 多相共存时，各相的组成和数量不随时间而改变
4、化学平衡（chemical equilibrium ） 反应系统中各物的数量不再随时间而改变
三、状态函数 系统的一些性质，其数值仅取决于系统所处
的状态，而与பைடு நூலகம்统的历史无关；
它的变化值仅取决于系统的始态和终态，而
热和功的取号与热力学能变化的关系 系统吸热
Q>0 环境 U >0 系统
系统放热
Q<0 U <0 W<0 对环境作功
U = Q + W
W>0 对系统作功
例1：体系由A态变化到B态，沿途径Ⅰ放热100J， 对体系做功50J，问①由A态沿途经Ⅱ到B态，体系 做功80J，则Q为多少？②如果体系再由B态沿途经 Ⅲ回到A态，得功为50J，体系是吸热还是放热， Q为多少？ Ⅱ Ⅰ A Ⅲ 系统变化框图

第一章热力学第一定律本章主要公式及其使用条件一、热力学第一定律W Q U +∆＝ W Q dU δδ+=热力学中规定体系吸热为正值，体系放热为负值；体系对环境作功为负值，环境对体系作功为正值。

功分为体积功和非体积功。

二、体积功的计算体积功：在一定的环境压力下，体系的体积发生改变而与环境交换的能量。

体积功公式⎰⋅-=dV p W 外 1 气体向真空膨胀：W ＝0 2气体在恒压过程：)(12 21V V p dV p W V V --=-=⎰外外3理想气体等温可逆过程：2112ln lnp p nRT V V nRT W -=-= 4理想气体绝热可逆过程：)(12,T T nC W U m V -=∆＝理想气体绝热可逆过程中的p ，V ，T 可利用下面两式计算求解1212,ln ln V V R T T C m V -=21,12,ln lnV V C p p C m p m V =三、热的计算热：体系与环境之间由于存在温度差而引起的能量传递形式。

1. 定容热与定压热及两者关系定容热：只做体积功的封闭体系发生定容变化时， U Q V ∆= 定压热：只做体积功的封闭体系定压下发生变化， Q p = ΔH定容反应热Q V 与定压反应热Q p 的关系：V p Q Q V p ∆+= nRT U H ∆+∆=∆n ∆为产物与反应物中气体物质的量之差。

或者∑+=RT g Q Q m V m p )(,,ν ∑+∆=∆RT g U Hm m)(ν式中∑)(g ν为进行1mol 反应进度时，化学反应式中气态物质计量系数的代数和。

2.热容 1.热容的定义式dTQ C δ=dT Q C VV δ=dT Q C pp δ=n CC VmV =,n C C p m p =, C V ，C p 是广度性质的状态函数，C V ，m ，C p,m 是强度性质的状态函数。

2.理想气体的热容对于理想气体 C p ,m － C V ,m =R 单原子理想气体 C V ，m = 23R ；C p ,m = 25R 双原子理想气体 C V ,m =25R ；C p ,m = 27R 多原子理想气体： C V ,m = 3R ；C p ,m = 4R通常温度下，理想气体的C V ,m 和C p,m 均可视为常数。

1.1.2.3 过程和途径
1.过程：当体系的状态发生变化时，状态变 化的经过，强调变化的方式 2.途径：完成变化的具体步骤，强调经由路 径的不同
注： 过程和途径不是严格区分的两个概念， 不强调方式和路径的时候可通用
几种常见的过程
• 等/定温过程：体系始态、终态及过程中的温度等于环境 温度且为常数。 T始=T终=T体=T环=常数 • 等/定压过程：体系始态、终态及过程中的压力等于环境 压力且为常数。 p始=p终=p体=p环=常数 • 等/定容过程：在变化过程中，体系的容积始终保持不变。 V体=常数

二次恒外压压缩
体系返回原状态，体系虽然恢复原 态，但环境失去功，得到热
等温可逆膨胀
V2 WⅣ nRT ln V1
W WⅣ WⅣ 0 , 又U Q W 0, 则Q 0
等温可逆压缩 V1 WⅣ nRT ln V2
体系循原过程返回，不仅体系恢复原态，而且未给 环境留下功热转化的痕迹，即环境也恢复原状态
1.1.3.1 能量守恒定律
1840年左 右，焦耳 发现了热 功当量
1.1.3.1 能量守恒定律
热功当量
升高相同的温度
状态1 加热 W=0 状态2 热 功 当 量
Q=0
Q=0
机械功 电功
1.1.3.1 能量守恒定律
电量热法
1.1.3.1 能量守恒定律
机械量热法
1.1.3.1 能量守恒定律
到1850年，科学界公认能量守恒定律是自然界的普 遍规律之一。
1.1.3.3 “热一”数学表达 式
Q
W
W
U1
Q
U2
U2-U1 = Q+W
1.1.3.3 “热一”数学表达式

第一章 热力学第一定律核心内容：能量守恒 ΔU=Q+W主要内容：三种过程（单纯pVT 变化、相变、化学反应）W 、Q 、ΔU 、ΔH 的计算一、内容提要1．热力学第一定律与状态函数（1）热力学第一定律： ΔU=Q+W （封闭系统） 用途：可由ΔU ，Q 和W 中的任意两个量求第三个量。

（2）关于状态函数（M ）状态函数：p 、V 、T 、U 、H 、S 、A 、G ……的共性： ①系统的状态一定，所有状态函数都有定值；②系统的状态函数变化值只与始终态有关，而与变化的途径无关。

用途：在计算一定始终态间的某状态函数增量时，为了简化问题，可以撇开实际的复杂过程，设计简单的或利用已知数据较多的过程进行计算。

ΔM （实）=ΔM （设）。

这种方法称为热力学的状态函数法。

③对于循环过程，系统的状态函数变化值等于零，即ΔM =0。

此外，对于状态函数还有如下关系：对于组成不变的单相封闭系统，任一状态函数M 都是其他任意两个独立自变量（状态函数）x 、y 的单值函数，表示为M=M(x 、y)，则注意：因为W 和Q 为途径函数，所以Q 和W 的计算必须依照实际过程进行。

⎰-=21V V a m bdV p W ，其中p amb 为环境压力。

Q 由热容计算或由热力学第一定律求得。

dy y M dx x M dM xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂=)(1循环关系式-=⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂xM y M y y x x M )(22尤拉关系式xy My x M ∂∂∂=∂∂∂1（p 1,V 1,T 1） （p'1,V 1,T 2） 2（p 2,V 2,T 2） （p 1,V'1,T 2） VT 将热力学第一定律应用于恒容或恒压过程，在非体积功为零（即w'=0）的情况下有：Q V =ΔU ，Q p =ΔH （H 的定义：H=U+pV ）。

此时，计算Q v 、Q p 转化为计算ΔU 、ΔH ，由于U 、H 的状态函数性质，可以利用上面提到的状态函数法进行计算。

引言：1．热力学是研究热与其他能量之间的转化规律；2．化学热力学——热力学在化学中的应用；②化学变化的方向和限度——热力学第二定律特点：①宏观性质——研究系统宏观性质，而不考虑微观结构和微观因素②只考虑系统的始末态，而不追究过程的细节和速率局限性：只能对现象之间的联系做宏观的了解，而不能作微观的说明或给出宏观性质的数值。

§1.1 基本概念一、系统和环境㈠定义系统：研究对象，包括物质，空间环境：与系统紧密相关的外界㈡系统分类①敞开系统：系统与环境有物质和能量的交换②封闭系统；系统与环境无物质交换，有能量交换③隔离系统: 系统与环境无物质和能量的交换二、状态与状态函数※1.状态：系统趋于某一确定的热力学平衡态（力平衡、热平衡、化学平衡、相平衡）状态函数：描述状态的宏观物理学量（宏观量：温度T、体积V、压强P、熵S、焓H……）☆☆☆注意：⑴状态一定，状态函数一定；状态函数一定，状态一定（单一值）。

⑵只要有一个状态函数改变，状态就改变。

⑶状态的确定：ⅰ.单组分密闭均相系统，只要指定两个状态函数，状态就一定，而其他的状态函数Z将随之而定，因为Z=F(T,P).ⅱ.K种物质的多组分系统，指定T、P、X1、X2、X3...Xk-1，状态一定，Z=F(T、P、X1、X2、X3...Xk-1)(K个组分的浓度要一一指定).2.状态函数的特点：⑴状态一定，状态函数值一定。

⑵状态函数的改变量只取决于始末态，与途径无关△Z=∫dZ=Z末-Z初⑶系统循环一周，状态改变量为零，△Z=∮dZ=0.3.状态函数的全微分性Z=F(T、P)微小变化dZ=(dZ/dT)p dT+(dZ/dP)T dP4.状态函数的分类是否具有加和性：⑴广度性质——v、n、H、S...与物质的量有关，具有加和性⑵强度性质——T、P、M...自身特性，不具加和性两个广度性质之比=强度性质如，V m=V/n，C=n/V.三、过程和途径过程：任何状态的改变①等温过程：T初=T末=T环=常数②等压过程：P初=P末=P外=常数●恒外压过程：P初≠P末=P外=常数③等容过程：体积不变，△V=0.④绝热过程：系统与环境无热交换（爆炸瞬间）⑤循环过程：初态经过某个过程又回到初态，△Z=0.途径：初态到达末态具体的步骤.四、功和热※1.定义：热（Q）——系统与环境间由于温差所传递的能量功（W）——除热以外的其他所能传递的能量2.系统吸热Q为正，Q>0;放热Q为负，Q＜0.系统对环境做功W为负，W＜0；环境对系统做功，W为正，W ＞0.3.功和热不是状态函数，其值与途径有关.4.功的分类：其他功Wf（电功、表面功…）体积功dW=-P外dV W=∫- P外dV=-P外（V2-V1）5．功的计算方法①等容过程：△V=0或dV=0，W=∫- P外dV=0.②自由膨胀：P外=0，W=∫- P外dV=0.③恒外压过程：P外=常数，W=∫- P外dV=-P外（V2-V1）.④等压过程：P1=P2=P外=常数，W=∫- P外dV=-P外（V2-V1）. 例1：1mol理想气体由27℃、101.325Kpa在外压恒定为831400Pa下压缩到27℃,0.003m3,求压缩功。

封闭系统 ， 从状态 1 变为状态 2 ，此系统热力学能的
改变ΔU为：
ΔU = U2 - U1 = Q +W
d U = δQ +Δw
若系统所发生的变化非常微小，则：
——热力学第一定律的数学表达式
二、热力学能
热力学能，亦称为内能，它是指系统内部能量的总 和，包括分子运动的平动能、转动能、振动能、电子能、 核能以及位能等。热力学能用符号U表示。
胀次数无限多，系统自始至终是对抗最大的阻力情况
下，所以此过程所作的功为最大功。这种过程称为准 静态过程。
二、不同过程的体积功
准静态膨胀过程： 若气体为理想气体，且为 等温膨胀，则
V1 p
W4
V2
V
W4
V2
V1
pdV
V2
V1
V2 nRT dV nRT ln V V1
二、不同过程的体积功
T,p Zn s 2HCl aq ZnCl2 aq H 2 g
请问这是什么体系，界面在什么位置？
思考与讨论
3、如果物体A分别与物体B、C达到温度一致，则 物体B和C是否达到热力学平衡态？ 4、某体系可以从状态B变化到状态A，也可以从 状态C变化到状态A，这两种状态A以及各种状 态函数在此两种状态A的数值是否完全相同？ 5、理想气体向真空膨胀，当一部分气体进入真空 容器后，余下的气体继续膨胀时所做的功是大
能量效应；
• 研究物理过程和化学变化的方向和限度。
二、化学热力学研究的内容
将热力学的基本原理应用于化学现象及与化学有关
的物理现象的规律的研究，就称为化学热力学。其主要
内容是利用：
热力学第一定律---计算化学变化中的热效应 热力学第二定律---计算变化的方向和限度，特别是化 学反应的可能性以及平衡条件的预示。

四、可逆过程与体积功
2、理想气体的定温膨胀（压缩）次数与功值关系
T1＝300K p1＝5大气压
n＝1mol
p p1
T2＝300K p2＝1大气压
n＝1mol
p 1 V1
1次膨胀
W p（V2 V1） 0.8RT
p2 V1 p2 V 2 V2 V


四、可逆过程与体积功 p
p1 p1V1
CV
QV
dT
Cp
Q p
dT
∴
U CV dT T V
H Cp dT T p
QV
U QV CV dT
T1
T2
Qp
H Q p C p dT
T1
T2


六、热 容
1mol物质的定容摩尔热容可写作CV，m，CV＝nCV，m。 1mol物质的定压摩尔热容可写作Cp，m，Cp＝nCp，m。


六、热 容
4、求热公式
a、Q n Cm dT
T1
T2
b、Q UV n CV ,m dT nCV ,m T
T1
T2
c、Q H p n C p ,m dT nC p ,m T
T1
T2
例题四


七、热力学第一定律的应用
1、理想气体的内能与焓
焦耳实验
T 0 ∴ Q0
能量交换 可 可 有 有
不能有 不能有
不能有


二、热力学基本概念
广度性质和强度性质有如下关系：
广度性质 ＝强度性质 广度性质
V Vm n
强度性质 广度性质＝广度性质

系统的各种性质，它们均随 状态确定而确定。 如:T, p, V，n 又如:一定量n的理想气体 V=nRT/P V= f(T,P) T, P是独立变量 推广 X=f (x, y) 其变化只与始末态有关，与 变化途径无关。
途径 2
状态2 (T2，p2)
途径 1
状态 1 (T1，p1)
图1.2 状态与途径
6 3 6
1.4.2.可逆过程与不可逆过程
某过程进行之后系统恢复原状的同时，环境也 恢复原状而未留下任何永久性的变化，则该过程 称为热力学可逆过程。
图1.5 恒外压膨胀
图1.6 可逆膨胀
热力学可逆过程有以下特征
（1）可逆过程进行时，系统始终接近于平衡态。 （2）可逆过程进行时，过程的推动力与阻力只相 差无穷小。 （3）系统进行可逆过程时，完成任一有限量变化 均需无限长时间。 （4）在定温可逆过程中，系统对环境所做之功为最 大功；环境对系统所做之功为最小功。
P16例题1 ：在298K时2molH2的体积为15dm3 ， 此时气体（1）在定温条件下，反抗外力为105Pa时 膨胀到体积为50dm3；（2）在定温下，可逆膨胀 到体积为50dm3。试计算两种膨胀过程的功。 解： (1)过程为不可逆过程 P外= P1= P2 = 105Pa
W p外 (V2 V1 ) [105 (50 15) 103 ]J 3500 J
p2 =-p1V1 (1- )=-V1 (P1 -P2 ) p1
=-10 10-3 m3 (106 -105 )Pa=-9.0 103 J
(3)外压比内压小一个无穷小的值，等温膨胀 过程是无限缓慢。
p1 p1 W pdV nRT ln p1V1 ln p2 p2

δ w = p外 dV
考虑下述理想气体的等温过程的体积功
w = ∫ p外 dV
V1
V2
普遍性 公式
1-4 可逆过程与不可逆过程 ( Reversible and Irreversible process) （1）向真空膨胀 ） （2）等容过程 ） （3）恒外压过程 ） （4）等压过程 ）
w=0 w=0
(5) 体积功（膨胀功 expansion work）： 体积功（ ） 当系统的体积变化时，系统反抗环境 压力所作的功。
δ w = p外 dV
δw：微小数量的功 ：
P外
V
1-3 热力学第一定律 The first law of thermodynamics
1. 能量转化与守恒定律 Joule 实验 2. 内能（internal energy) 内能（ 热力学能（ 热力学能（thermodynamic energy ) (1) 内能是组成体系的所有粒子的各种运动 和相互作用的能量的总和。 (2) 内能是系统的状态函数
则
∂F ∂F ∂F ∂z = + ∂x y ∂x z ∂z x ∂x y
此公式是以下数学处理方法的结果： 令：F = f ( x, z )
∂F ∂F 则 dF = dx + dz ∂x z ∂z x
（2）力平衡（mechanical equilibrium) ）力平衡（ 如果没有刚性壁存在， 如果没有刚性壁存在，系统各部分之 间，系统与环境之间没有不平衡的力存在
在不考虑重力场与其它外场作用的情况下， 系统内部处处压力相等
（3）相平衡（phase equilibrium) ）相平衡（ 相（phase) 系统内物理性质及化学性质完全均匀 的一部分称为一相。

第⼀章热⼒学第⼀定律第⼀章热⼒学第⼀定律本章基本要求1．理解掌握体系、环境、状态函数的概念2．理解掌握内能、热和功的概念和相互关系3．理解焓的物理意义4．掌握热⼒学第⼀定律的应⽤5．理解热容的概念及有关计算6．熟练计算过程的内能、焓的改变量以及热和功的数值本章难点1．状态函数的概念2．热和功为什么是传递的能量3．焓的物理意义4．焦⽿汤姆逊试验的含义以及实际⽓体过程的△H ,△U的计算（⼀）热⼒学概论1－1 热⼒学的研究对象把物理学中最基本的原理应⽤于研究化学现象以及与化学现象有关的物理现象，则称为化学热⼒学，在化学界，也简称热⼒学。

化学热⼒学的主要内容是利⽤热⼒学第⼀定律来计算变化过程中的能量转换问题；利⽤热⼒学第⼆定律来寻求变化的⽅向和限度问题以及相平衡、化学平衡等问题。

例如:碳1化学，氮肥的合成，⽯墨制⾦刚⽯。

热⼒学研究的对象是由⼤量分⼦组成的宏观集合体，这是热⼒学的最⼤特点。

这个特点也就决定了热⼒学⽅法的优点和缺点。

缺点：1、不考虑物质的微观结构和反应进⾏的机理2、所研究的变量中没有时间概念；3、知其然不知其所以然。

1－2 热⼒学基本概念与术语⼀、系统（体系）和环境体系：作为研究对象的那部分物质（微观组成的宏观集合体）环境：与体系密切相关的其他部分。

系统与环境间有实在或假想的界⾯隔开。

物理化学中所研究的体系，根据体系与环境之间能量和物质的交换情况，分成三类：1、敞开体系：体系和环境之间，既有物质的传递，⼜有能量的传递的体系。

2、密闭（封闭）体系：体系和环境之间，仅有能量的传递，没有物质传递的体系。

封闭体系中⼜可分出⼀类，体系和环境之间没有物质的交换，也没有热能的交换，只有功的交换，这类体系称为绝热体系。

物理化学主要讨论封闭体系和绝热体系。

3、孤⽴（隔绝）体系：体系和环境之间，既⽆物质交换⼜⽆能量交换的体系。

⼆、体系的性质、状态和状态函数体系是我们研究的对象。

我们把体系的性质的总和称为体系的状态（在热⼒学中状态是指平衡态），或系统的状态即系统所处的样⼦。

3、系统的性质（宏观性质）
（1）广度性质：与系统所含物质的量有关，具有 加和性。（如质量、体积等） （2）强度性质：与系统所含物质的量无关，不具有 加和性。（如温度、压力、密度等） 在一定条件下，广度性质可以转化为强度性质。
m V
第一章 热力学第一定律
二、状态与状态函数
1、状态：系统内所有宏观性质的总和。
第一章 热力学第一定律
§1-1 基本概念
一、系统与环境
1、概念：在热力学上将作为研究对象的那部分物质 称为系统；将与之有密切联系（即可能有 物质或能量交换）的其余部分称为环境。 系统
环境
第一章 热力学第一定律
说明：系统与环境的界面可以是实际存在的，
也可以无界面。
例如：以我们现在上课的教室为例
（1）如果以人为系统，则周围的空气就是环境； （系统与环境之间有界面） （2）如果以人和教室内的空气为系统，则教室外面的
U 1
B
U 2
循环都有多余的能量产生，违背
热力学第一定律。 所以 U 1 U 2
A
第一章 热力学第一定律 3、系统状态发生变化时，其内能的改变量是一定的， 但在实现这一状态变化的各个可能过程中，热和功可以 有不同的值。
例如：对于反应
Zn + CuSO4 = Cu + ZnSO4
每当有1mol 锌置换出1mol铜时，系统地内能减少249.4kJ。 即：U 249.4kJ / mol （1）途径Ⅰ：将锌片直接插入硫酸铜水溶液中； （2）途径Ⅱ：将锌片与铜片构成原电池。
2、符号规定：
（1）环境对系统做功时，W ＞ 0； （2）系统向环境做功时，W ＜ 0。
第一章 热力学第一定律
3、功的类型