第一章热力学第一定律及其应用
- 格式:ppt
- 大小:1.29 MB
- 文档页数:149





热力学第一定律的表述方式及应用热力学第一定律是热力学中的基本定律之一,也被称为能量守恒定律。
它指出,在任何一个热力学系统中,系统的内能变化等于系统所吸收的热量与对外做的功的代数和。
这一定律为我们理解和描述热力学系统的行为提供了重要的理论依据。
一、热力学第一定律的表述方式热力学第一定律可以用以下三种方式进行表述:1. 微分形式在微分形式下,热力学第一定律可以表示为:[ = Q - W ]其中,( U ) 表示系统的内能,( Q ) 表示系统吸收的热量,( W ) 表示系统对外做的功。
2. 积分形式在积分形式下,热力学第一定律可以表示为:[ U = Q - W ]其中,( U ) 表示系统内能的变化量,( Q ) 表示系统吸收的热量,( W ) 表示系统对外做的功。
3. 宏观形式在宏观形式下,热力学第一定律可以表示为:[ _{i=1}^{n} i = {j=1}^{m} _j ]其中,( _i ) 表示系统从第 ( i ) 个热源吸收的热量,( _j ) 表示系统对外做第 ( j )项功。
二、热力学第一定律的应用热力学第一定律在工程、物理等领域有着广泛的应用,下面列举几个常见的应用实例:1. 热机效率的计算热机效率是指热机所做的功与吸收的热量之比。
根据热力学第一定律,热机所做的功等于吸收的热量减去内能的变化量。
因此,热机效率可以表示为:[ = ]2. 制冷机的性能分析制冷机的工作原理是利用工作物质在循环过程中吸收热量,从而实现低温环境的创造。
根据热力学第一定律,制冷机吸收的热量等于制冷量与制冷机压缩机所做的功之和。
因此,可以通过热力学第一定律来分析制冷机的性能。
3. 太阳能热水器的设计太阳能热水器利用太阳能将光能转化为热能,为用户提供热水。
根据热力学第一定律,太阳能热水器吸收的热量等于水温升高所吸收的热量与热水器损失的热量之和。
因此,在设计太阳能热水器时,需要考虑热量的损失,以提高热水器的效率。
4. 热传导过程的分析热传导是热量在物体内部由高温区向低温区传递的过程。
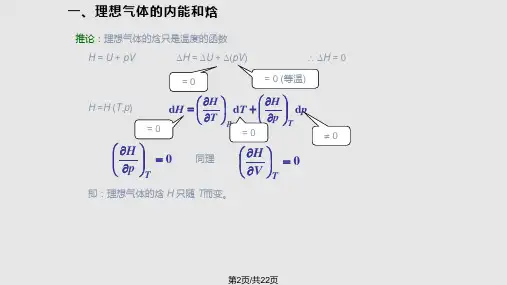

热力学第一定律,又称热力学第一定律原理或热力学第一定律定理,是热力学的基本定理之一。
它指出:在任意一个过程中,物质的总热力量Q和总功率W之和是定值,即Q+W=定值。
热力学第一定律的实际运用广泛,可以用来解决各种热力学问题。
下面给出几个具体的例子。
制冷机的工作原理:制冷机是利用制冷剂的汽化-冷凝-膨胀过程来进行冷却的。
制冷剂从低压汽化到高压气体的过程中,汽化所吸收的热量就是制冷机所发出的冷量。
这个过程可以看作是制冷机消耗的功率W,对应的热力学第一定律式为Q+W=定值。
热水器的工作原理:热水器是利用电能将水加热的。
电能转化成热能的过程可以看作是热水器消耗的功率W,加热水所吸收的热量就是热水器发出的热量Q。
这个过程可以用热力学第一定律来表示,即Q+W=定值。
汽车发动机的工作原理:汽车发动机是利用燃料的燃烧来产生动力的。
燃料的燃烧过程中,消耗的燃料质量就是汽车发动机的功率W,燃烧所释放的热量就是汽车发动机发出的热量Q。
这个过程可以用热力学第一定律来表示,即Q+W=定值。
光伏发电的工作原理:光伏发电是利用光能转化成电能的过程。
光能转化成电能的过程可以看作是光伏发电的功率W,光伏发电所产生的电能就是光伏发电发出的热量Q。
这个过程可以用热力学第一定律来表示,即Q+W=定值。
以上就是热力学第一定律的几个具体运用例子。
可以看出,热力学第一定律是一个非常重要的定理,在各种热力学过程中都有着广泛的应用。


物理化学-第⼀章热⼒学第⼀定律及其应⽤练习题-140第⼀章热⼒学第⼀定律及其应⽤练习题⼀、热⼒学第⼀定律基础1、任⼀循环过程,若系统经历的变化有⼏步,则(C)Q+W=0 (D) Q=W>0请选择答案:A B C D2、⼀理想⽓体系统,压⼒由5p?⼀步等温膨胀⾄p?,做功W1,交换热Q1,再由p?⼀步压缩⾄5 p?,做功W2,交换热Q2,则不正确的是:A.Q1+Q2=-W1-W2B.|W1|>|W2|C.|W1|=|W2|D.|Q1|<|Q2|请选择答案:A B C D(提⽰:|? V|相同,反抗的外压不同。
?U1=0,?U2=0)3、?U=Q+W适⽤于:A.各种系统的热⼒学过程。
B.开放系统和封闭系统的热⼒学过程。
C.封闭系统和孤⽴系统的热⼒学过程。
D.孤⽴系统和开放系统的热⼒学过程。
4、第⼀个确定功和热相互转换的定量关系的科学家是:A ⽡特B 卡诺C 焦⽿D 迈尔5、在⼀绝热恒容容器中盛有⽔,⽔中放有电阻丝,由容器外的蓄电池给电阻丝供电,若以⽔为系统,则下⾯的关系中正确的是:(A)W>0,Q>0,?U>0 (B)W=0,Q>0,?U=0(C)W<0,Q>0,?U>0 (D)W=0,Q=0,?U=06、⽤电阻丝加热烧杯中的⽔,若以⽔中的电阻丝为系统,则下⾯的关系中正确的是:(A)W>0,Q<0,?U>0 (B)W=0,Q>0,?U>0(C)W=0,Q<0,?U<0 (D)W<0,Q>0,?U>07、⼀电冰箱的压缩机⼯作时,若冰箱为系统,则下⾯的关系中正确的是:(A)W>0,Q<0,?U>0 (B)W>0,Q<0,?U<0(C)W=0,Q<0,?U<0 (D)W<0,Q>0,?U>08、电解稀H2SO4⽔溶液时,若以此溶液及电解产物为系统则下⾯的关系中正确的是:(A)W>0,Q>0,?U>0 (B)W<0,Q>0,?U>0(C)W<0,Q>0,?U<0 (D)W>0,Q<0,?U>09、2 mol理想⽓体,在温度T时,由压⼒2p?⼀次膨胀到p?,系统所做的功为:A.W=-4RTB.W=-2RTC.W=-1/2(RT)D.W=-RT(提⽰:W=- p?(V2-V1)=- p?V1=- p?*nRT/(2p?) = -0.5nRT = -RT10、4 mol理想⽓体N2(g),由温度T绝热压缩⾄温度1.5T,则环境所做的功为:A.W=4RTB.W=3RTC.W=5RTD.W=10RT请选择答案:11、在温度T和压⼒p?下反应 CH3CH2OH(g)=C2H4(g)+H2O(g)的反应进度为2mol,若⽓体作理想⽓体处理,则功A. W=2RTB. W=-2RTC. W=RTD. W=-RT请选择答案:12、54g H2O(g)在温度T和压⼒p?下凝结成H2O(l)时,则过程中的功为:A. W=3RTB. W=-3RTC. W=2RTD. W=-2RT请选择答案:13、2mol理想⽓体在温度T,由体积V可逆变⾄2V,则过程中的功为:A.W=nRTln2B.W=-nRTln2C.W=RTD.W=-RT(提⽰:W=-nRTln(V2/V1)=-nRTln2)14、⼀理想⽓体系统,由体积V1变为V2(V1>V2),温度不变,分别经历⼀步,两步,三步和⽆限多步四条途径,相应的功为W1,W2,W3和W n,则下⾯的关系中正确的是:A.W1B. W1=W2=W3=W n,C.W1>W2>W3>W n C. W115、2mol理想⽓体Ar由温度T经⽆限慢且⽆耗散效应的绝热过程达到体积1.5V,温度1.5T,该过程中的功约为:A. W=-3RTB. W=-2RTC. W=-RTD. W=-6RT请选择答案:16、n mol理想⽓体,经绝热过程由温度T1、体积V1和压⼒P1变⾄体积0.8V1,压⼒2.5P1,该⽓体的C p,m与C v,m之⽐为1.4,该过程中的功约为:A. W= nR(T1-T2)B. W= nR(T2-T1)C. W=5nR1 D. W=2.5nRT1请选择答案:17、44g⼲冰在压⼒p?和温度T下,全部变为⽓体,该过程中的功约为:A.W=-RTB.W=-2RTC.W=RTD.W=3RT(提⽰:W=- p?(V2-V1)≈ - p?V2=-RT)18、Carnot循环由等温可逆膨胀、绝热可逆膨胀、等温可逆压缩和绝热可逆压缩4个连续的步骤构成,各步的功⽤W1,W2,W3和W4表⽰,则下⾯的关系中正确的是:(A)W1< W2< W3< W4 (B) W1< W2< W4< W3(C)W1> W2> W3> W4 (D)W1> W2> W4 > W319 n mol理想⽓体,由体积V1和压⼒P1⾃由膨胀致体积2V1,压⼒0.5P1,该过程中的功约为:A. W=-0.5nRTB.W=-nRTC. W=0D.W=-2nRT请选择答案:20、⼀理想⽓体,初态压⼒100kpa,体积10dm3,绝热指数为1.4,经绝热可逆膨胀⾄5dm3,终态压⼒为:(A)2.639P1(B)2P1(C)1.319P1(D)0.758P121、⼀理想⽓体,若由同⼀始态A(P1,V1)分别经可逆等温膨胀和绝热可逆膨胀⾄终态B(P2,V2)与C(P2',V2),前⼀过程的功W1,后⼀过程的功W2,再由B态和C态经可逆等温压缩和绝热可逆压缩⾄原态A, 前⼀过程的功W3,后⼀过程的功W4,则: (A)W1> W2> W3> W4 (B) W3< W4< W2< W1(C)W1> W3> W2> W4 (D)W3> W4> W2 > W122、1mol理想⽓体,由温度T和压⼒P1可逆等温膨胀⾄0.25P1,过程中的功为:(A)W=-3RT (B)W=-RTln4(C)W=-RT (D)W=RTln423、n mol理想⽓体,经绝热过程由P1,V1,T1变为P2,V2,T2,若P2=4P1,V2=0.5V1,则A.T1/T2=2B.T1/T2=0.25C.T1/T2=0.5D.T1/T2=4(提⽰:P1V1/T1=P2V2/T2,T1/T2=P1V1/P2V2=P1V1/4*0.5P1V1=0.5) 24、在温度T和压⼒P?下,反应 NH3(g)+HCl(g)=NH4Cl(s) 的进度为1mol时,过程中的功为:(A)W=- RT (B)W=2RT(C)W= RT (D)W=-2RT25、在373.15K和压⼒p?下,36g H2O(g)变为H2O(l),若已知H2O(l)的⽓化热为40.66kJ/mol,则下⾯的关系中正确的是: (A) H= (81320+2RT)J (B)Q=(81320+2RT)J(C)?U=(-81320+2RT)J (D)?U=(-81320-2RT)J26、若反应H2(g)+(1/2)O2(g)=H2O(g)在孤⽴系统中进⾏,则下⾯的关系中不正确的是:(A)? U=0 (B)W=0(C)? H=0 (D)Q=0(提⽰:?H=?U+?(PV)=?U+V?P,?P≠0)27、2mol理想⽓体N2定容升温,T2=1.25T1,则下⾯关系中正确的是:(A)?U=(3/4)×T1R (B)?H=(5/4)×T1R (C)Q=(7/4)×T1R (D)H=(7/4)×T1R28、4mol理想⽓体K r,等压降温,T2=(4/5)×T1,则下⾯关系中正确的是:(A)? U=-(6/5)×T1R (B)=-2T1R(C)?H=-(14/5)×T1R (D)Q=-(5/6)×T1R29、若某化学反应A(s)+M2N(aq)=AN(aq)+M2(g)在等温等压下于电池中进⾏,做电功150kJ,体积功2.5kJ,放热120kJ,则下⾯关系中正确的是:(A)?r H m=-120kJ (B)W=152.5kJ(C)?U=-272.5kJ (D)Q=?r H m=-120kJ(提⽰:?U=Q+W=-120-152.5=-272.5)30、2mol双原⼦分⼦理想⽓体,在温度T下反抗压⼒p?由体积V1膨胀⾄2V1,下⾯的关系中正确的是:(A)?H m>0 (B)?U>0(C)?U=W (D)Q=RT31、2mol理想⽓体H2(g),经绝热压缩后,体积和压⼒由P1V1变为2P1V1,下⾯的关系中正确的是:(A)?H=5RT1(B)?U=2.5RT1(C)?U=5RT1 (D)?H=7RT132、当⽓体由节流膨胀⽽降温时,下⾯的说法中不正确的是:(A)等焓过程(B)绝热不可逆过程(C)多孔塞两边压⼒恒定不变(D)温度随压⼒的变化率⼩于零33、对节流膨胀,下⾯的说法中正确的是:A.节流系数⼤于零,发⽣加热效应。
第一章热力学第一定律及其应用第一节热力学概论一、热力学的目的和内容目的:热力学是研究能量相互转换过程中所应遵循的规律的科学。
广义的说,热力学是研究体系宏观性质变化之间的关系,研究在一定条件下变化的方向和限度。
主要内容是热力学第一定律和第二定律。
这两个定律都是上一世纪建立起来的,是人类经验的总结,有着牢固的实验基础。
本世纪初又建立了热力学第三定律。
化学热力学:用热力学原理来研究化学过程及与化学有关的物理过程就形成了化学热力学。
化学热力学的主要内容:1. 利用热力学第一定律解决化学变化的热效应问题。
2. 利用热力学第二律解决指定的化学及物理变化实现的可能性、方向和限度问题,以及相平衡、化学平衡问题。
3. 利用热力学第三律可以从热力学的数据解决有关化学平衡的计算问题。
二、热力学的方法及局限性方法:以热力学第一定律和第二定律为基础,经过严谨的推导,找出物质的一些宏观性质,根据物质进行的过程前后某些宏观性质的变化,分析研究这些过程的能量关系和自动进行的方向、限度。
由于它所研究的对象是大数量分子的集合体,因此,所得结论具有统计性,不适合于个别分子、原子等微观粒子,可以说,此方法的特点就是不考虑物质的微观结构和反应机理,其特点就决定了它的优点和局限性。
局限性:1. 它只考虑平衡问题,只计算变化前后总账,无需知道物质微观结构的知识。
即只能对现象之间联系作宏观了解,不能作微观说明。
2. 它只能告诉我们在某种条件下,变化能否发生,进行的程度如何,而不能说明所需的时间、经过的历程、变化发生的根本原因。
尽管它有局限性,但仍为一种非常有用的理论工具。
热力学的基础内容分为两章,热力学第一定律和第二定律,在介绍两个定律之前,先介绍热力学的一些基本概念及术语。
三、热力学基本概念1. 体系与环境体系:用热力学方法研究问题时,首先要确定研究的对象,将所研究的一部分物质或空间,从其余的物质或空间中划分出来,这种划定的研究对象叫体系或系统(system)。
第一章热力学第一定律本章主要公式及其使用条件一、热力学第一定律W Q U +∆= W Q dU δδ+=热力学中规定体系吸热为正值,体系放热为负值;体系对环境作功为负值,环境对体系作功为正值。
功分为体积功和非体积功。
二、体积功的计算体积功:在一定的环境压力下,体系的体积发生改变而与环境交换的能量。
体积功公式⎰⋅-=dV p W 外 1 气体向真空膨胀:W =0 2气体在恒压过程:)(12 21V V p dV p W V V --=-=⎰外外3理想气体等温可逆过程:2112ln lnp p nRT V V nRT W -=-= 4理想气体绝热可逆过程:)(12,T T nC W U m V -=∆=理想气体绝热可逆过程中的p ,V ,T 可利用下面两式计算求解1212,ln ln V V R T T C m V -=21,12,ln lnV V C p p C m p m V =三、热的计算热:体系与环境之间由于存在温度差而引起的能量传递形式。
1. 定容热与定压热及两者关系定容热:只做体积功的封闭体系发生定容变化时, U Q V ∆= 定压热:只做体积功的封闭体系定压下发生变化, Q p = ΔH定容反应热Q V 与定压反应热Q p 的关系:V p Q Q V p ∆+= nRT U H ∆+∆=∆n ∆为产物与反应物中气体物质的量之差。
或者∑+=RT g Q Q m V m p )(,,ν ∑+∆=∆RT g U Hm m)(ν式中∑)(g ν为进行1mol 反应进度时,化学反应式中气态物质计量系数的代数和。
2.热容 1.热容的定义式dTQ C δ=dT Q C VV δ=dT Q C pp δ=n CC VmV =,n C C p m p =, C V ,C p 是广度性质的状态函数,C V ,m ,C p,m 是强度性质的状态函数。
2.理想气体的热容对于理想气体 C p ,m - C V ,m =R 单原子理想气体 C V ,m = 23R ;C p ,m = 25R 双原子理想气体 C V ,m =25R ;C p ,m = 27R 多原子理想气体: C V ,m = 3R ;C p ,m = 4R通常温度下,理想气体的C V ,m 和C p,m 均可视为常数。
目录(试卷均已上传至“百度文库”,请自己搜索)第一章热力学第一定律及其应用物化试卷(一)第一章热力学第一定律及其应用物化试卷(二)第二章热力学第二定律物化试卷(一)第二章热力学第二定律物化试卷(二)第三章统计热力学基础第四章溶液物化试卷(一)第四章溶液物化试卷(二)第五章相平衡物化试卷(一)第五章相平衡物化试卷(二)第六章化学平衡物化试卷(一)第六章化学平衡物化试卷(二)第七章电解质溶液物化试卷(一)第七章电解质溶液物化试卷(二)第八章可逆电池的电动势及其应用物化试卷(一)第八章可逆电池的电动势及其应用物化试卷(二)第九章电解与极化作用第十章化学动力学基础(一)物化试卷(一)第十章化学动力学基础(一)物化试卷(二)第十一章化学动力学基础(二) 物化试卷(一)第十一章化学动力学基础(二) 物化试卷(二)第十二章界面现象物化试卷(一)第十二章界面现象物化试卷(二)第十三章胶体与大分子溶液物化试卷(一)第十三章胶体与大分子溶液物化试卷(二)参考答案1.物质的量为n的纯理想气体,该气体在如下的哪一组物理量确定之后,其它状态函数方有定值。
( )(A) p (B) V (C) T,U (D) T, p2. 下述说法哪一个正确? ( )(A) 热是体系中微观粒子平均平动能的量度(B) 温度是体系所储存热量的量度(C) 温度是体系中微观粒子平均能量的量度(D)温度是体系中微观粒子平均平动能的量度3. 有一高压钢筒,打开活塞后气体喷出筒外,当筒内压力与筒外压力相等时关闭活塞,此时筒内温度将:( )(A)不变(B)升高(C)降低(D)无法判定4. 1 mol 373 K,标准压力下的水经下列两个不同过程变成373 K,标准压力下的水气,(1) 等温等压可逆蒸发,(2)真空蒸发这两个过程中功和热的关系为:( )(A) |W1|> |W2| Q1> Q2(B)|W1|< |W2| Q1< Q2(C) |W1|= |W2| Q1= Q2(D)|W1|> |W2| Q1< Q25. 恒容下,一定量的理想气体,当温度升高时热力学能将:( )(A)降低(B)增加(C)不变(D)增加、减少不能确定6. 在体系温度恒定的变化中,体系与环境之间: ( )(A) 一定产生热交换(B)一定不产生热交换(C) 不一定产生热交换(D)温度恒定与热交换无关7. 一可逆热机与另一不可逆热机在其他条件都相同时,燃烧等量的燃料,则可逆热机拖动的列车运行的速度:( )(A) 较快(B) 较慢(C) 一样(D) 不一定8. 始态完全相同(p1,V1,T1)的一个理想气体体系,和另一个范德华气体体系,分别进行绝热恒外压(p0)膨胀。