三垂线定理及其应用

立体几何：三垂线定理及其简单应用新课标高中数学中，淡化了“三垂线定理及逆定理”，但我们认为：三垂线定理还是非常好用的。

至少用它来证明有关题目，会简捷得多！（一）温故知新，引入课题大家已经学习了直线和平面的垂直关系，学新课之前，让我们作个简单的回顾：1．直线和平面垂直的定义？2．直线和平面垂直的判定定理?（二）猜想推测，激发兴趣（三）层层推进，证明定理我们在讨论立体空间时，通常会想把空间的问题转化为平面问题，那有没有什么方法可以帮助我们将空间与平面联系在一起呢? · 今天我们学习的内容，就可以把空间垂直的问题转化为平面垂直的问题。

这就是:三垂线定理与三垂线逆定理 .我们先来看一下三垂线定理及逆定理的描述。

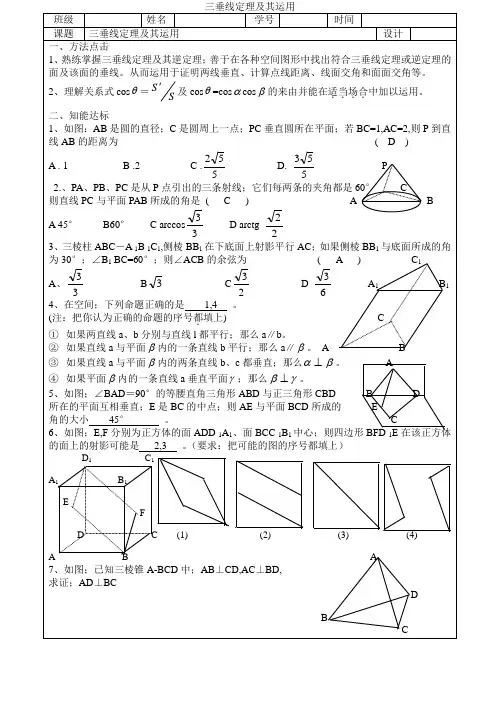
1、三垂线定理：平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

2、三垂线定理的逆定理：如果平面内一条直线和该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

具体在图中体现为：我们将OP称为平面的斜线，PA是平面的垂线，AO是OP在平面内的射影，a是平面内的一条直线，若a与AO 垂直，则l也与PO垂直，反之亦然。

其实三垂线定理从证明的角度看可以认为是线面垂直转化关系的一个常用推论.这是一个标准的从线线垂直（一般是共面）转化为线面垂直又转化为新的线线垂直（一般是异面）的立体几何推理过程。

但换一个观点和角度来看，三垂线定理的价值在于将一个需要进行多次转化而且模式基本确定的证明过程以定理的形式规范下来，这使得在相关的证明（之后还有计算）过程中书写难度得到有效降低，在部分复杂题目中更是如此。

而从很多立体几何题目设计的思路来看，经常会出现两条看似无关直线（一般是异面）的关系问题，一般方法是让他们在不同平面中分别找关系，然后利用一个桥梁进行沟通；三垂线定理正是提供了这样一个可以进行简便沟通的方式。

而更为重要的是，在三垂线定理中，最重要的其实并不是斜线或者射影（尽管它们分别是条件和结论），而是平面的垂线！有了这个垂线的存在，才会使得两条异面直线建立关系；有了这个垂线，才能形成相应的平面和直角三角形从而便于计算；而同样也是因为有了这条垂线，使得直线和平面所称的角，以及升级版的平面和平面所成的角（二面角）出现并有了用平面角度量其大小的方式。

三垂线定理知识点总结一、三垂线定理的定义三垂线定理是指在一个三角形中，三条垂线经过一个顶点交于同一点。

具体来说，如果在一个三角形中，我们分别从三个顶点做垂线，那么这三条垂线会相交于同一个点，这个点就叫做三角形的垂心。

垂心是三角形内心的一种特殊情况，也是三角形的一个重要点。

二、三垂线定理的性质1. 三角形的垂心是三角形内心的一种特殊情况。

2. 三角形的垂心到三条边的距离相等。

3. 垂心到三角形三个顶点的连线叫做垂径，垂心到垂径的距离相等。

4. 垂心到三角形三个顶点的连线叫做垂线，垂心到垂线的距离最小。

5. 三角形的三个垂线相交于同一个点。

三、三垂线定理的证明三垂线定理的证明需要借助一些平面几何的知识和方法。

一般来说，我们可以采用反证法来证明三垂线定理，具体步骤如下：1. 假设垂心不是三个垂线的交点，即存在一个点不受三个垂线的影响。

2. 利用垂线的定义和性质，通过绘制辅助线和辅助角等方法，得出矛盾结论。

3. 由矛盾推出假设错误，即证明垂心是三个垂线的交点。

三垂线定理的证明比较复杂，需要结合具体的题目和图形进行推敲，但掌握了相关的证明方法后，就可以轻松应对各种类型的证明题目。

四、三垂线定理的应用三垂线定理在解题中有着广泛的应用，特别是在证明题和计算题中。

下面通过几个例题的分析，来展示三垂线定理的应用。

例1：如图，在△ABC中，AD ⊥ BC，BE ⊥ AC，CF ⊥ AB，垂足分别为D，E，F，连接AD，BE，CF相交于H。

证明：H是△ABC的垂心。

解：根据题意可知，H是由AD，BE，CF三个垂线相交而成的交点，而AD，BE，CF分别是△ABC三条边的垂线，所以H是△ABC的垂心。

例2：如图，点P是△ABC内部一点，PA，PB，PC分别交△ABC的边BC，CA，AB于D，E，F。

证明：若P为△ABC的垂心，则△DEF的三条边和面积与△ABC的相似。

解：首先我们可以利用三垂线定理来证明P是△ABC的垂心，然后我们可以利用相似三角形的性质来证明△DEF与△ABC的相似性。

三垂线定理及证明三垂线定理是几何学中的重要定理之一。

它指出，在一个三角形中，从顶点向对边作垂线，这些垂线的交点将会共线。

这一定理的证明可以通过几何推理来完成。

我们来考虑一个任意的三角形ABC。

我们从顶点A向边BC作垂线AD，从顶点B向边AC作垂线BE，从顶点C向边AB作垂线CF。

我们的目标是证明这三条垂线所在的线段DF是共线的。

为了证明这一点，我们需要使用一些基本的几何定理和性质。

首先，我们知道在一个直角三角形中，垂线会相交于直角顶点。

所以，我们可以得出结论，AD与BC相交于点D，BE与AC相交于点E，CF与AB相交于点F。

接下来，我们需要证明点D、E、F三者共线。

我们可以通过反证法来进行证明。

假设点D、E、F不共线，即它们不在同一条直线上。

那么我们可以得出结论，线段DE与线段DF不平行，且线段EF与线段DF不平行。

现在我们来考虑三个小三角形，即三角形ADE、三角形BEF和三角形CDF。

由于线段DE与线段DF不平行，根据平行线性质可知，∠DAE与∠DFA不等。

同理，根据线段EF与线段DF不平行，可知∠FEB与∠FDB不等。

从而我们可以得到结论，∠DAE + ∠FEB + ∠FDB ≠ 180°，这与三角形内角和定理相矛盾。

因此，我们可以推断出点D、E、F必须共线。

这就证明了三垂线定理。

三垂线定理在几何学中有着广泛的应用。

首先，在解决三角形相关问题时，我们可以利用三垂线定理来推导出一些有用的结论。

例如，通过三垂线定理，我们可以证明三角形的垂心存在，即三条垂线的交点。

垂心在三角形的性质研究中有着重要的地位。

三垂线定理也可以用于解决一些几何问题。

例如，在解决平面几何问题时，我们可以利用三垂线定理来推导出一些几何关系，从而简化问题的解决过程。

总结起来，三垂线定理是几何学中的重要定理之一。

它指出，在一个三角形中，从顶点向对边作垂线，这些垂线的交点将会共线。

这一定理可以通过几何推理来证明，其证明过程中运用了一些基本的几何定理和性质。

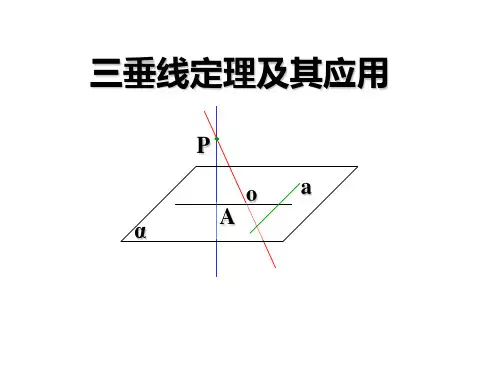
三垂线定理及其逆定理•正射影的概念：自一点向平面引垂线，垂足叫做这一点在平面内的正射影（简称为射影）；平面的斜线的概念：如果一条直线和一个平面相交但不垂直，那么这条直线叫做这个平面的斜线，斜线和平面的交点叫做斜足。

•三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

•三垂线定理与其逆定理的关系：即：•三垂线定定理的主要应用：证明线线、线面垂直，求点到线的距离、二面角大小。

应用两个定理解题的一般思路：平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

证明：1）用线面垂直证明已知：如图，PO在α上的射影OA垂直于a三垂线定理的证明三垂线定理的证明求证：OP⊥a证明：过P做PA垂直于α∵PA⊥α且a⊆α∴a⊥PA又a⊥OAOA∩PA=A∴a⊥平面POA∴a⊥OP（2）用向量证明三垂线定理1.已知：PO，PA分别是平面α的垂线，斜线，OA是PA在α内的射影，向量b包含于α，且向量b垂直于OA，求证：向量b垂直于PA证明：∵PO垂直于α，∴PO垂直于b，又∵OA垂直b，向量PA=（向量PO+向量OA）∴向量PA·向量b=（向量PO+向量OA）·向量b=（向量PO·向量b）+（向量OA·向量b ）=0，∴PA⊥向量b。

2.已知三个平面OAB，OBC，OAC相交于一点O，∠AOB=∠BOC=∠COA=60度，求交线OA与平面OBC所成的角。

解：∵向量OA=（向量OB+向量AB），O是内心，又∵AB=BC=CA，∴OA与平面OBC所成的角是30°。

用途在做图中，做二面角的平面角在证明中，证明线线垂直在计算中，用归纳法归拢已知条件，便于计算口诀线射垂，线斜垂；线斜垂，线射垂。

浅谈对三垂线定理模型的了解和熟练运用
三垂线定理是一种重要的几何学定理，是数学领域里著名的古典定理之一，也
是几何学领域中最重要的定理，由古希腊数学家尼萨德先生所提出。

它指明了在一个三角形中，任意一条垂线到各条边的距离之和等于另一条垂线到同样的边的距离之和。

通俗地说，就是当三角形三边的一个垂足与另两边构成的两个直角三角形的等腰三角形，其他的垂足到同样的两边的距离之和等于在一路边上的两个垂足到对应两边的距离之和。

它只涉及到三角形，是一种有关它自身内部条件的研究。

三垂线定理可以帮助我们快速解决三角形里的各种几何问题，如内外和平面角，质心和外心等，平时也可以把它应用到求解体育运动、法律继承问题中去，当遇到复杂的几何问题时，只要我们熟练掌握三垂线定理，就能够帮助我们在解题中获得更多的线索，大大提高解题的效率。

三垂线定理简单易懂，但要想恰到好处地运用它，需要广泛运用数学知识，在
实际解题之前要把问题想清，运筹帷幄，全面梳理出问题中存在的条件，对关键条件进行分析和评估，这样才能让解题过程更加顺利，最终获得更优质的解答。

三垂线定理是一种重要的几何学定理，无论是求解几何问题还是用于涉及其他
范畴的应用，都可以有效地帮助人们更加快捷地解决问题。

因此，想要熟练掌握三垂线定理，细心分析问题，把握出垂线定理的逻辑关系，利用之精准求解，是我们应尽的义务之一。

三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。

在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。

换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。

证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。

点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。

考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。

根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。

将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。

应用：利用三垂线定理，可以方便地计算三角形的面积。

设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。

由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。

三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。

需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。

解析几何中的三垂线定理解析解析几何是数学中的一个重要分支，它研究了点、线、面等几何图形在坐标系中的性质和关系。

在解析几何中，三垂线定理是一个基本而重要的定理，它揭示了三角形内部垂线的性质和关系。

本文将对三垂线定理进行解析，探讨其含义和应用。

一、三垂线定理的表述三垂线定理是指对于任意一个三角形ABC，它的三条垂线AD、BE、CF相交于一个点O，并且这个点O到三个顶点的距离满足以下关系：OA^2 + OB^2 +OC^2 = OD^2 + OE^2 + OF^2。

二、三垂线定理的证明要证明三垂线定理，我们可以利用向量的性质来进行推导。

首先，设三角形ABC的顶点A、B、C的坐标分别为(Ax, Ay)，(Bx, By)，(Cx, Cy)。

设垂足D的坐标为(Dx, Dy)。

根据向量的性质，我们可以得到向量AD、BD和CD的表达式：AD = (Dx - Ax, Dy - Ay)BD = (Dx - Bx, Dy - By)CD = (Dx - Cx, Dy - Cy)由于AD与向量AB的夹角为90度，所以它们的点积为0。

同理，BD与向量BC的点积也为0，CD与向量CA的点积也为0。

根据点积的性质，我们可以得到以下方程：(AB)·(AD) = 0(BC)·(BD) = 0(CA)·(CD) = 0将向量的表达式带入上述方程，可以得到：(Ax - Bx)(Dx - Ax) + (Ay - By)(Dy - Ay) = 0(Bx - Cx)(Dx - Bx) + (By - Cy)(Dy - By) = 0(Cx - Ax)(Dx - Cx) + (Cy - Ay)(Dy - Cy) = 0将上述方程展开并整理，可以得到：Ax^2 + Ay^2 - 2(Ax * Dx + Ay * Dy) + Dx^2 + Dy^2 - AB^2 = 0Bx^2 + By^2 - 2(Bx * Dx + By * Dy) + Dx^2 + Dy^2 - BC^2 = 0Cx^2 + Cy^2 - 2(Cx * Dx + Cy * Dy) + Dx^2 + Dy^2 - CA^2 = 0将上述方程相加得到：2(Dx^2 + Dy^2) = AB^2 + BC^2 + CA^2进一步整理可以得到：OD^2 + OE^2 + OF^2 = OA^2 + OB^2 + OC^2因此，三垂线定理得证。