厚壁圆筒应力

厚壁圆筒应力分析剖析一、应力分析方法1.在应力分析中，通常采用静力学的方法，根据力学定律对厚壁圆筒进行应力分析。

2.厚壁圆筒的应力分析可以分为轴向应力、周向应力和切向应力三个方向上的应力分析。

二、应力计算公式1.轴向应力：σa=(P·r)/t其中，σa表示轴向应力，P表示圆筒受到的内外压力，r表示圆筒内径，t表示圆筒壁厚。

2.周向应力：σc=(P·r)/(2t)其中，σc表示周向应力。

3. 切向应力：τ = (P · ri) / t其中，τ 表示切向应力，ri 表示圆筒中心点到任意一点的径向距离。

三、实例分析假设有一个内径为 10cm，外径为 15cm，壁厚为 2cm 的厚壁圆筒，内外压力分别为 5MPa 和 10MPa。

现对该厚壁圆筒进行应力分析。

1.轴向应力：根据公式σa = (P · r) / t，代入 P = 5MPa，r = 7.5cm，t =2cm，计算得σa = (5×7.5) / 2 = 18.75MPa。

同理，代入 P = 10MPa，r = 7.5cm，t = 2cm，计算得σa =(10×7.5) / 2 = 37.5MP a。

2.周向应力：根据公式σc = (P · r) / (2t)，代入 P = 5MPa，r = 7.5cm，t= 2cm，计算得σc = (5×7.5) / (2×2) = 9.375MPa。

同理，代入 P = 10MPa，r = 7.5cm，t = 2cm，计算得σc =(10×7.5) / (2×2) = 18.75MPa。

3.切向应力：根据公式τ = (P · ri) / t，代入 P = 5MPa，ri = 7.5cm，t =2cm，计算得τ = (5×7.5) / 2 = 18.75MPa。

同理，代入 P = 10MPa，ri = 7.5cm，t = 2cm，计算得τ =(10×7.5) / 2 = 37.5MPa。

工程上一般将设计压力在10≤p≤100MPa之间的压力容器称为高压容器，而将100MPa压力以上的称为超高压容器。

高压容器不但压力高，而且同时伴有高温，例如合成氨就是在15～32MPa压力和500℃高温下进行合成反应。

一般来说，高压和超高压容器的径比K > 1.2，称此类容器为“厚壁容器”。

本章讨论的对象，是厚壁圆筒型容器。

承受压力载荷或者温差载荷的厚壁圆筒容器，其上任意点的应力，是三向应力状态。

即存在经向应力（又称轴向应力）、周向应力和径向应力。

针对厚壁筒的应力求解，将在平衡方程、几何方程、物理方程三个方面进行分析。

2.2.1 弹性应力－压力载荷引起的弹性应力（1）轴向(经向)应力ϭz222200002200002220()1i z i i i i i i i z i iP P FP P p R p R F R R p R p R p p KR K R R K R σππππσ−=−=⋅−⋅=−−−⋅===−−径比(2) 周向应力ϭ和径向应力ϭrθ三对截面：一对圆柱面，相距dr一对纵截面，相差dθ一对横截面，长度为1Ϭz作用在横截面上Ϭr作用在圆柱面上Ϭθ作用在纵截面上平衡方程（沿径向列平衡方程）()()112sin 102r r r d d r dr d rd dr θθσσθσθσ++⋅−⋅−⋅=sin 22d d θθ≈略去高阶无穷小，并使得到平衡方程r r d r drθσσσ−=几何方程()r w dw wdwdr drε+−==径向应变周向应变()r w d rd wrd r θθθεθ+−==上述表达式是Lame 在1833年推得的，又称为Lame 公式。

当仅有内压时，p o =0，有()222222211111112i o i o r z i z r p R K r p R K r p K θθσσσσσσ⎧⎛⎞=⋅−⎪⎜⎟−⎝⎠⎪⎪⎛⎞⎪=⋅+⎜⎟⎪−⎝⎠⎨⎪⎛⎞=⋅⎪⎜⎟−⎝⎠⎪⎪=+⎪⎩246810010********σθ R i / σθ R oK可见，当K 越大时，应力的分布就越不均匀。

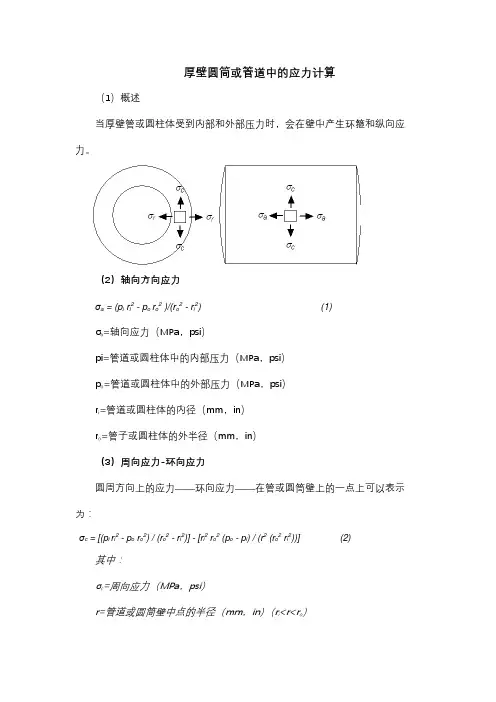
厚壁圆筒或管道中的应力计算（1）概述当厚壁管或圆柱体受到内部和外部压力时，会在壁中产生环箍和纵向应力。

（2）轴向方向应力σa = (p i r i2 - p o r o2 )/(r o2 - r i2) (1)σa=轴向应力（MPa，psi）pi=管道或圆柱体中的内部压力（MPa，psi）p o=管道或圆柱体中的外部压力（MPa，psi）r i=管道或圆柱体的内径（mm，in）r o=管子或圆柱体的外半径（mm，in）（3）周向应力-环向应力圆周方向上的应力——环向应力——在管或圆筒壁上的一点上可以表示为：σc = [(p i r i2 - p o r o2) / (r o2 - r i2)] - [r i2 r o2 (p o - p i) / (r2 (r o2 r i2))] (2)其中：σc=周向应力（MPa，psi）r=管道或圆筒壁中点的半径（mm，in）（r i<r<r o）r=r i时的最大应力（管道或圆柱体内部）(4)合成应力气缸壁中单个点的组合应力不能通过使用矢量加法的单个矢量来描述。

相反，可以使用描述两个物理向量之间的线性连接的应力张量（矩阵）。

径向应力管壁或圆筒壁中某一点处的径向应力可以表示为：σr= [(p i r i2 - p o r o2) / (r o2 - r i2)] + [r i2 r o2 (p o - p i) / (r2 (r o2 - r i2))] (3) r=r o时的最大应力（管道或圆柱体外部）(5)示例-厚壁圆筒中的应力在内径为200mm（半径为100mm）、外径为400mm（半径为200mm）的圆柱体中，相对于外部压力存在100MPa的压力。

轴向应力可计算为:σa=（（（100 MPa）（100 mm）2-（0 MPa）（200 mm）2）/（（200 mm =33.3 MPa内壁（100 mm）的周向应力（环向应力）可计算为:σc=[（（100 MPa）（100 mm）2-（0 MPa）（200 mm）2）/（200 mm=167 MPa内壁（100 mm）的径向应力可计算为:σr=[（（100 MPa）（100 mm）2-（0 MPa）（200 mm）2）/（200 mm=-100MPa。

厚壁圆筒应力分析1、概述K>1.2的壳体成为厚壁圆筒。

厚壁容器承压的应力特点有（此处不考虑热应力）：一、不能忽略径向应力，应做三向应力分析；二、厚壁容器的应力在厚度方向不是均匀分布，而是应力梯度。

所以，在求解的时候需要联立几何方程、物理方程、平衡方程才能确定厚壁各点的应力大小。

2、解析解一、内压为i p ，外压为0p 的厚壁圆筒，需要求出径向应力r σ、周向应力θσ和轴向应力z σ，其中轴向应力z σ不随半径r 变化。

（1）几何方程如图所示，取内半径r ，增量为dr 的一段区域两条弧边的径向位移为ω和ωωd +，其应变的表达式为：r rd rd d r drd dr d r ωθθθωεωωωωεθ=-+==-+=))(（周向应力：径向应力：（1）θσ对r 求导，得：()θθσσωωωωωσ-=⎪⎭⎫⎝⎛-=-='⎪⎭⎫ ⎝⎛=r rr dr d r r r dr d r dr d 112 （2） （2）物理方程 根据胡克定理表示为[]z Eσσμσεθθ+-=r (1（3） 两式相减，消去z σ得：[]θθσσμεε-+=r E ）（1-r []z r Eσσμσεθ+-=(1r（4） 将（4）代入（2）得：[]）z r Edr d σσμσεθθ+-=(1（5） 对（3）的θε求导得，z σ看做常数：⎪⎭⎫⎝⎛-=dr r d dr d E dr d σμσεθθ1 （6） 联立（5）、（6）得：[]θθθσσμσμσ-)1-r rdr d dr d +=（ （7） （3）平衡方程如图所示，沿径向和垂直径向建立坐标 系，把θσ向x 轴和y 轴分解，得：⎪⎭⎫ ⎝⎛=-+2sin 2θθd p p p r dr r （8）其中()θσσd dr r d p r r dr r ++=+)（ （9）θσrd p r r =由于θd 很小，22sin θθd d ≈⎪⎭⎫⎝⎛，略去二阶微量r r d d σ，得 drd rrr σσσθ=- （10） 联立（7）（10）得0322=+drd dr d r r r σσ （11）对（11）进行求得r σ，在代入（10）得22rBA rB A r +=-=θσσ （12） 其中A 、B 是两个积分常数，要求A ，B 需要两个方程，根据内外壁边界条件0,,p R r p R r r i r i -==-==σσ （13）将（13）代入（12）得：22020202202002)(ii i i i i RR R R p p B R R R p R p A --=--=（14）最后剩下z σ未求出，最后在轴向用平衡方程，内力等于外力。

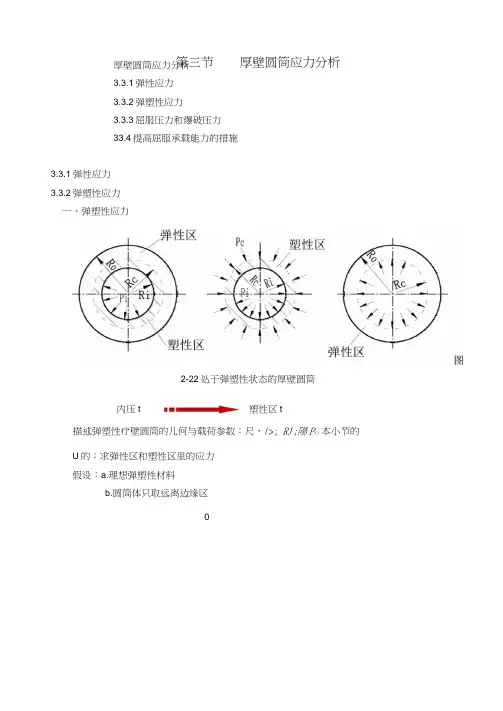
厚壁圆筒应力分析3.3.1弹性应力 3.3.2弹塑性应力3.3.3屈服压力和爆破压力33.4提高屈服承载能力的措施3.3.1弹性应力 3.3.2弹塑性应力一、弹塑性应力描述弹塑性疗壁圆筒的儿何与载荷参数：尺，/>; RJ;陽P () 本小节的U 的：求弹性区和塑性区里的应力假设：a.理想弹塑性材料b.圆筒体只取远离边缘区第三节 厚壁圆筒应力分析内压t 塑性区t2-22处于弹塑性状态的厚壁圆筒图2-23理想弹•塑性材料的应力■应变关系1、塑性区应力平衡方程：刃-旦drMises屈服失效判据:CF e-丐=—=丁2联立积分，得<T r=-^trJnr+Ar = &：6=-Pi内壁边界条件，求出A后带回上式得将r = R e: cr r= -p c代入(2-42)得2 ! R<p(=--a s ln-+Pl结论：① b = pjbj②q, cr^=/(lnr) rt,③cr：=-(b「+ b&) H const (区别:弹区cr. =-© + b&) =const )2 2弹性区内壁处于屈服状态:（刃）Y一（6）“ =眉$Kc=Ro/Rc(2-46)(2-26) (2-40) (2-41)将(2-42)带入(2-40)得(2-42 )(2-43)(2-44 )(2-45 ) 山表2J拉美公式得出:与2-45联立导出弹性区与塑性区交界面的pi与Rc的关系Pi =由（2-34）式（以代代替门）得若按屈雷斯卡（H.Tresca）屈服失效判据，也可导岀类似的上述各表达式。

各种应力表达式列于表2-4中结论：② 6 a d=f(r) rT->(r z. T,与「无关二、残余应力肖厚壁圆筒进入弹塑性状态后卸除内爪力pi —残余应力思考：残余应力是如何产生的卸载定理：卸载时应力改变量Ab = b-b和应变的改变量△£ = £-£之间存在着弹性关系= 图2・24。

厚壁圆筒应力分析剖析厚壁圆筒是一种常见的结构，广泛应用于各个领域，比如压力容器、热交换器等。

在使用厚壁圆筒的过程中，必须进行应力分析，以确保结构的安全性和可靠性。

首先，研究厚壁圆筒的应力分析需要考虑以下几个方面。

1.圆筒的几何形状：厚壁圆筒是由外径、厚度和长度组成的。

这些几何参数会影响圆筒内部的应力分布情况。

2.材料特性：圆筒的材料特性直接影响其应力分布。

研究厚壁圆筒时，通常会考虑材料的弹性模量和泊松比等参数。

3.加载条件：圆筒的应力分布受外部载荷的影响。

载荷的形式可以是压力、温度、重力等。

加载条件的确定对于应力分析至关重要。

接下来，我们将详细介绍厚壁圆筒的应力分析方法。

1.内外压力分析：考虑厚壁圆筒内外的压力差异。

当内外压力相等时，圆筒应力较小。

当内压大于外压时，圆筒将会受到较大的应力。

2.纵向应力分析：厚壁圆筒在纵向方向上承受的应力主要为轴向拉应力。

如果存在压力差，则拉应力沿厚度逐渐增加。

3.周向应力分析：在周向上，厚壁圆筒受到的应力主要为周向拉应力。

当圆筒内外压力不平衡时，周向应力将会增加。

4.切应力分析：切应力是圆筒内部的剪切应力分量。

在圆筒壁厚度的不同位置，切应力的大小也会有所不同。

5.应力分布图：为了更好地理解厚壁圆筒的应力分布情况，可以绘制应力分布图。

这样可以直观地了解不同部位的应力分布情况，以便进行结构优化。

总结一下，厚壁圆筒的应力分析对于确保结构安全性至关重要。

通过分析内外压力、纵向应力、周向应力和切应力，可以更好地理解圆筒的应力分布情况。

通过应力分布图，可以更直观地了解圆筒不同部位的应力情况，从而进行优化设计。

在实际工程中，应力分析的结果可以用来指导材料的选择、结构的设计以及使用中的安全操作。

05_压力容器应力分析_厚壁圆筒弹性应力分析压力容器是广泛应用于石油、化工、冶金、医药等行业的重要设备，用于存储和运输气体或液体。

在使用过程中，由于内外压差的存在，压力容器的壁会产生应力，如果超过了材料的极限承载能力，就会发生破裂事故。

因此，对压力容器的应力分析非常重要，通过分析容器内壁的应力分布情况，可以判断容器的安全性能，从而采取相应的措施保证其安全运行。

厚壁圆筒作为一种常见的压力容器结构，其应力分析是非常有代表性的。

在进行弹性应力分析时，首先需要确定内压力和外压力的大小。

通常情况下，我们假设容器的内部和外部都是完全承受压力的，即容器内部压力和外部压力均匀分布。

其次，我们需要了解容器的内径、外径、壁厚等几何参数，以及容器所使用的材料的弹性模量和泊松比等弹性性质参数。

在厚壁圆筒的弹性应力分析中，一般采用极限状态设计方法进行计算。

首先，可以根据容器内外压力差的大小，计算容器内部的径向应力和环向应力，这两个应力分量是产生破裂的主要因素。

然后，通过应力的叠加原理，将径向应力和环向应力合成为合成应力，进一步计算合成应力与容器材料的屈服强度之间的比值，根据这个比值可以评估容器的安全性能。

在实际应用中，为了保证压力容器的安全性能，通常会将容器的设计和制造有一定的安全裕量。

在计算容器的弹性应力时，需要将其与容器材料的屈服强度进行比较，以确保应力值处于安全范围内。

如果计算得到的应力值超过了材料的屈服强度，就需要重新设计容器的结构或者更换更高强度的材料，以满足安全性能的要求。

总之，压力容器的应力分析是确保容器安全运行的重要手段之一、通过对容器内壁的应力分布进行分析，可以评估容器的安全性能，并采取相应的措施保证其安全运行。

在进行压力容器的设计和制造过程中，应该遵循相应的规范和标准，确保容器的结构和材料能够承受内外压力的作用，从而保证容器在工作过程中不会发生破裂事故，保障工业生产和人身安全。

第二章 厚壁圆筒的弹塑性应力分析1.只受内压作用：（1）在厚壁圆筒中，筒体处于三向应力状态，其中θσ为拉应力，r σ为压应力，且沿壁厚非均匀分布；而z σ介于θσ和r σ之间，即2r z θσσσ+=，且沿壁厚均匀分布。

（2）在筒体内壁面处，θσ、r σ的绝对值比外壁面处为大，其中θσ具有最大值，且恒大于内压力i p ，其危险点将首先在内壁面上产生。

（3）θσ沿壁厚分布随径比K 值的增加趋向更不均匀，不均匀度为内、外壁周向应力之比，即2()1()2io r R r R K θθσσ==+=。

显然，不均匀度随2K 成比例，可见K 值愈大，应力分布愈不均匀。

当内壁材料开始屈服时，外壁材料远小于屈服限，因此筒体材料的强度不能得到充分的利用。

由此可知，用增加筒体壁厚（即增加K 值）的方法来降低厚壁圆筒的内壁应力，只在一定范围内有效，而内压力接近或超过材料的许用应力时，增加厚度是完全无效的。

为了提高筒壁材料的利用率，有效的办法是改变应力沿壁厚分布的不均匀性，使其趋于均化。

2.往往采用组合圆筒或单层厚壁圆筒自增强处理技术，以提高筒体的弹性承载能力。

3.温差应力：厚壁圆筒的厚壁可能从内表面或外表面被加热，由于筒壁较厚，并有一定的热阻，在筒体的内、外壁之间存在温度差，温度较高部分因受热而引起膨胀变形，同时受到温度较低部分的约束，从而使前者受压缩，而后者受拉伸，出现了温差应力或称热应力。

（1）厚壁圆筒中，温差应力与温度差t ∆成正比，而与温度本身的绝对值无关，因此在圆筒内壁或外壁进行保温以减小内、外壁的温度差，可以降低厚壁圆筒的温差应力。

（2）温差应力的分布规律为三向应力沿壁厚均为非均匀分布，其中，轴向应力是环（周）向应力与径向应力之和，即t t t z r θσσσ=+ ；在内、外壁面处，径向应力为零，轴向应力和环（周）向应力分别相等，且最大应力发生在外壁面处。

（3）温差应力是由于各部分变形相互约束而产生的，因此应力达到屈服极限而屈服时，温差应力不但不会继续增加，而且在很大程度上会得到缓和，这就是温差应力的自限性，它属于二次应力。

厚壁圆筒平面应力问题和平面应变问题下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!Certainly! Here's a structured demonstration article on the topic "Thickwalled Cylinder: Plane Stress and Plane Strain Problems" in Chinese:厚壁圆筒的平面应力问题与平面应变问题。

图 厚壁圆筒问题
问题描述及要求
如图所示为一厚壁圆筒，其内半径r 1=50 mm ，外半径r 2=100 mm ，作用在内孔上的压力p=10 MPa ，无轴向压力，轴向长度很大可视为无穷。

材料参数：2e11（弹性模量），泊松比：0.3；计算厚壁圆筒的径向应力σr 和切向应力σt 沿半径r 方向的分布。

根据材料力学的知识，σr 、σt 沿r 方向的分布的解析解为
⎪
⎪⎭
⎫
⎝⎛--=2222
1
2221r 1r r r r p
r σ ⎪⎪⎭
⎫ ⎝⎛+-=222212221t 1r r r r p r σ
提示：该问题符合平面应变问题的条件，故可以简化平面应变问题进行分析。

另外，根据对称性，可取圆筒的四分之一并施加垂直于对称面的约束进行分析。

利用路径操作。

（1）
步骤：
1、定义单元类型
Ok
options
2、定义材料属性
3、创建模型
4、划分单元
Size controls--lines--set
apply
拾取圆弧边输入20
mesh
5、施加约束
apply
拾取左边线
6、施加载荷
7、求解
8、显示单元
Plot--elements
9、定义路径
顺次拾取下边线结点
Plot paths Map onto path
10、作路线图
11、结果。