岩土常用土的本构模型

岩土类材料弹塑性力学模型及本构方程TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-岩土类材料的弹塑性力学模型及本构方程摘要：本文主要结合岩土类材料的特性，开展研究其在受力变形过程中的弹性及塑性变形的特点，描述简化的力学模型特征及对应的适用条件，同时在分析研究其弹塑性力学模型的基础上，探究了关于岩土类介质材料的各种本构模型，如M-C、D-P、Cam、D-C、L-D及节理材料模型等，分析对应使用条件，特点及公式，从而推广到不同的材料本构模型的研究，为弹塑性理论更好的延伸发展做一定的参考性。

关键词：岩土类材料，弹塑性力学模型，本构方程不同的固体材料，力学性质各不相同。

即便是同一种固体材料，在不同的物理环境和受力状态中，所测得的反映其力学性质的应力应变曲线也各不相同。

尽管材料力学性质复杂多变，但仍是有规律可循的，也就是说可将各种反映材料力学性质的应力应变曲线，进行分析归类并加以总结，从而提出相应的变形体力学模型。

第一章岩土类材料地质工程或采掘工程中的岩土、煤炭、土壤，结构工程中的混凝土、石料，以及工业陶瓷等，将这些材料统称为岩土材料。

岩土塑性力学与传统塑性力学的区别在于岩土类材料和金属材料具有不同的力学特性。

岩土类材料是颗粒组成的多相体，而金属材料是人工形成的晶体材料。

正是由于不同的材料特性决定了岩土类材料和金属材料的不同性质。

归纳起来，岩土材料有3点基本特性：1.摩擦特性。

2.多相特性。

3.双强度特性。

另外岩土还有其特殊的力学性质：1.岩土的压硬性，2.岩土材料的等压屈服特性与剪胀性，3.岩土材料的硬化与软化特性。

4.土体的塑性变形依赖于应力路径。

对于岩土类等固体材料往往在受力变形的过程中，产生的弹性及塑性变形具备相应的特点，物体本身的结构以及所加外力的荷载、环境和温度等因素作用，常使得固体物体在变形过程中具备如下的特点。

固体材料弹性变形具有以下特点：(1)弹性变形是可逆的。

常用土体本构模型及其特点小结山中一草线弹性模型线弹性模型遵从虎克定律，只有2个参数，即弹性模量E和泊松比V,它是最简单的应力-应变关系，但无法描述土的很多特征，主要应用于早期的有限元分析及解析方法中，可用来近似模拟较硬的材料如岩土。

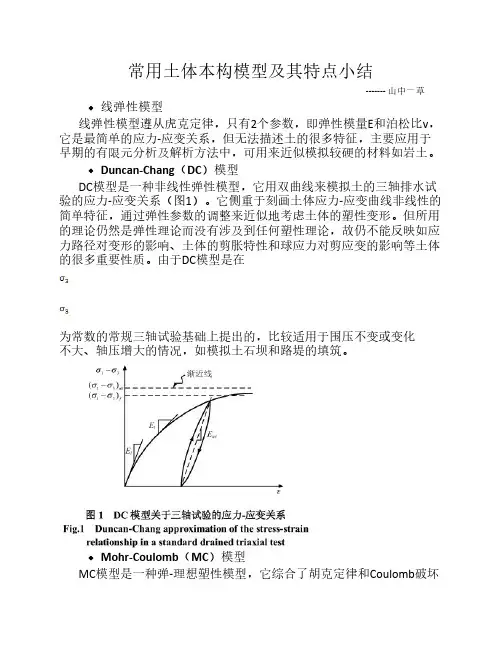
Duncan-Chang（ DC 模型DC模型是一种非线性弹性模型，它用双曲线来模拟土的三轴排水试验的应力-应变关系（图1）。

它侧重于刻画土体应力-应变曲线非线性的简单特征，通过弹性参数的调整来近似地考虑土体的塑性变形。

但所用的理论仍然是弹性理论而没有涉及到任何塑性理论，故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。

由于DC模型是在二为常数的常规三轴试验基础上提出的，比较适用于围压不变或变化不大、轴压增大的情况，如模拟土石坝和路堤的填筑。

图】IK模型关于三轴试验的应力-应变关系Fig.l Duncan-Chang approxiniathm of the siress-strainrd nt kinship Ln ft standard drained triAxt*! te&lMohr-Coulomb （MC）模型MC模型是一种弹-理想塑性模型，它综合了胡克定律和Coulomb破坏准则。

有5个参数，即控制弹性行为的2个参数：弹性模量E和泊松比v及控制塑性行为的3个参数：有效黏聚力c、有效内摩擦角和剪胀角。

MC模型采用了弹塑性理论，能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律，因而并不能较好地描述土体在破坏之前的变形行为，且不能考虑应力历史的影响及区分加荷和卸荷。

故MC模型能较好地模拟土体的强度问题，MC模型的六凌锥形屈服面（图2）与土样真三轴试验的应力组合形成的屈服面吻合得较好，因此MC模型适合于低坝、边坡等稳定性问题的分析。

Drucker -Prager( DP)模型DP模型对MC模型的屈服面函数作了适当的修改，采用圆锥形屈服面（图3）来代替MC模型的六凌锥屈服面，易于程序的编制和进行数值计算。

常用土体本构模型及其特点小结------- 山中一草线弹性模型线弹性模型遵从虎克定律，只有2个参数，即弹性模量E和泊松比v，它是最简单的应力-应变关系，但无法描述土的很多特征，主要应用于早期的有限元分析及解析方法中，可用来近似模拟较硬的材料如岩土。

Duncan-Chang（DC）模型DC模型是一种非线性弹性模型，它用双曲线来模拟土的三轴排水试验的应力-应变关系（图1）。

它侧重于刻画土体应力-应变曲线非线性的简单特征，通过弹性参数的调整来近似地考虑土体的塑性变形。

但所用的理论仍然是弹性理论而没有涉及到任何塑性理论，故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。

由于DC模型是在为常数的常规三轴试验基础上提出的，比较适用于围压不变或变化不大、轴压增大的情况，如模拟土石坝和路堤的填筑。

Mohr-Coulomb（MC）模型MC模型是一种弹-理想塑性模型，它综合了胡克定律和Coulomb破坏准则。

有5个参数，即控制弹性行为的2个参数：弹性模量E和泊松比v及控制塑性行为的3个参数：有效黏聚力c、有效内摩擦角和剪胀角。

MC模型采用了弹塑性理论，能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律，因而并不能较好地描述土体在破坏之前的变形行为，且不能考虑应力历史的影响及区分加荷和卸荷。

故MC模型能较好地模拟土体的强度问题，MC模型的六凌锥形屈服面（图2）与土样真三轴试验的应力组合形成的屈服面吻合得较好，因此MC模型适合于低坝、边坡等稳定性问题的分析。

Drucker -Prager（DP）模型DP模型对MC模型的屈服面函数作了适当的修改，采用圆锥形屈服面（图3）来代替MC模型的六凌锥屈服面，易于程序的编制和进行数值计算。

它存在与MC模型同样地缺点，相对而言，在模拟岩土材料时，MC 模型较DP模型更加适合。

修正剑桥模型（MCC）MCC模型为等向硬化的弹塑性模型，它修正了剑桥模型的弹头形屈服面，采用帽子屈服面（椭圆形）（图4），以塑性体应变为硬化参数，能较好地描述黏性土在破坏之前的非线性和依赖于应力水平或应力路径的变形行为，MCC模型从理论上和试验上都较好地阐明了土体的弹塑性变形特征，是应用最为广泛的软土本构模型之一。

（完整word版）⼟的本构模型对⽐⼏种⼟的本构模型对⽐⼀、概述岩⼟⼯程数值分析离不开岩⼟本构关系，本构关系⼴义的讲是⾃然界中某种作⽤与该作⽤的效应两者之间的关系。

在岩⼟⼯程中本构关系即岩⼟的应⼒应变关系。

描述岩⼟本构关系的数学表达式即本构⽅程。

岩⼟⼯程问题数值分析的精度很⼤程度上取决于所采⽤的本构模型的实⽤性和合理性。

岩⼟材料本构模型的建⽴是通过实验⼿段确定各类岩⼟的屈服条件，以及选⽤合理的试验参数，再引⽤塑性⼒学基本理论，从⽽建⽴起岩⼟本构模型，本构模型还需要通过试验与现场测试的验证，这样才算形成⼀个⽐较完善的本构模型。

⽽⼀个合理的本构模型应该具备理论上的严格性、参数上的易确定性和计算机实现的可能性。

以下选取上课时讲到过的本构模型进⾏对⽐。

⼆、⼏种本构模型（不讨论尹嘉诚同学的弹性本构模型）1.拉德-邓肯模型（刘琪）拉德与邓肯根据对砂⼟的真三轴试验结果，提出的⼀种适⽤于砂类⼟的弹塑性模型。

该模型把⼟视为加⼯硬化材料，服从不相关联流动法则，硬化规律采⽤弹塑性功硬化规律，模型中规定的屈服函数由试验资料拟合得到。

拉德-邓肯模型主要是反映了剪切屈服。

后来拉德⼜增加了⼀个体积屈服⾯，形成了双屈服⾯模型。

1988年拉德⼜将它的双屈服⾯，组合成⼀个全封闭的光滑屈服⾯，⼜回复到单屈服⾯模型。

2.清华模型（丁⽻）清华模型是以黄⽂熙教授为⾸的清华⼤学研究组提出来的。

其主要特点在于不是⾸先假设屈服⾯函数和塑性势函数，⽽是根据试验确定的各应⼒状态下的塑性应变增量的⽅向，然后按照相适应流动规则确定其屈服⾯，再从试验结果确定其硬化参数。

因⽽是假设最少的弹塑性模型。

3.后勤⼯程学院模型（殷⾦龙）郑颖⼈及其学⽣提出。

基于⼴义塑性理论，采⽤分量塑性势⾯与分量屈服⾯；适⽤于应变硬化⼟体的静⼒计算，既可⽤于压缩型⼟体，也可⽤于压缩剪胀型⼟体，但不考虑应⼒主轴旋转；屈服条件通过室内⼟⼯试验获得。

4.南京⽔科所弹塑性模型（叶进龙）南京⽔利科学研究院沈珠江等提出的双屈服曲⾯弹塑性模型适⽤于软粘⼟，并服从⼴义塑性⼒学理论。

岩土本构模型原理及应用简述摘要：简述了岩土本构模型中弹性本构模型、弹塑性本构模型及粘弹塑性模型的建立、应用范围和局限性。

认为当前的岩土本构模型，简单便于计算的模型不能反映岩土真实的力学性状，而精细复杂的模型参数难以确定，难以推广应用。

直至现阶段还没有一种能适应任何条件的普遍本构模型，目前岩土本构模型研究有必要向这方面发展。

关键词：岩土弹性本构模型弹塑性本构模型粘弹塑本构模型在实际工程中岩土体常常有很复杂的应力-应变特性，如非线性、弹性、塑性、粘性以及剪胀性、应变硬化（软化）、各向异性等，同时受到应力路径、应力历史以及岩土的状态、组成、结构和温度不同程度的影响。

因此为了反映岩土真实的力学性状，必须建立较为复杂的本构模型。

而实际工程应用中，在满足一定的精度条件下，又要求简单实用。

虽然至今的岩土本构模型达数百种，但大体上分为下述几类：弹性模型、弹塑性模型、粘弹塑性模型等。

1 弹性本构模型弹性模型是建立在弹性理论基础上的本构模型。

最简单的是线弹性模型，即广义胡克定律。

非线性弹性模型一般可分为三类：Cauchy弹性模型、超弹模型和次弹性模型。

非线性弹性模型是线弹性模型的推广，按照拟合应力-应变曲线的形状分为：折线型、双曲线型、对数曲线型等。

按照采用的弹性系数又可分为E-μ（弹性模量-泊松比）非线性弹性模型，K-G（体积变形模量-切变模量）非线性弹性模型，以及用其他形式表示的弹性模型。

1.1 线弹性本构模型弹性是一种理想的固体特性。

实际土体在外载荷作用下，只有在应变很小时才发生弹性变形。

模拟土体应力应变性质的最古老、最简单的方法是采用线弹性模型，即假设土体应力一应变之间存在一一对应的线形关系：σij=F（εij），反映在土体应力一应变关系矩阵式{σ}=[D]{ε}中，弹性模量矩阵[D]是常量。

由于土体弹性性质的方向性决定了各线弹性模型独立弹性常数个数。

对一般的均质连续各向异性弹性体，有21个独立弹性常数，正交各向异性线弹性模型具有9个独立弹性常数，横观各向同性线弹性模型具有5个独立弹性常数，最简单的各向同性线弹性模型（虎克定律）具有2个独立弹性常数。

常用土体本构模型及其特点小结------- 山中一草➢线弹性模型线弹性模型遵从虎克定律，只有2个参数，即弹性模量E和泊松比v，它是最简单的应力-应变关系，但无法描述土的很多特征，主要应用于早期的有限元分析及解析方法中，可用来近似模拟较硬的材料如岩土。

➢Duncan-Chang（DC）模型DC模型是一种非线性弹性模型，它用双曲线来模拟土的三轴排水试验的应力-应变关系（图1）。

它侧重于刻画土体应力-应变曲线非线性的简单特征，通过弹性参数的调整来近似地考虑土体的塑性变形。

但所用的理论仍然是弹性理论而没有涉及到任何塑性理论，故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。

由于DC模型是在为常数的常规三轴试验基础上提出的，比较适用于围压不变或变化不大、轴压增大的情况，如模拟土石坝和路堤的填筑。

➢Mohr-Coulomb（MC）模型MC模型是一种弹-理想塑性模型，它综合了胡克定律和Coulomb破坏准则。

有5个参数，即控制弹性行为的2个参数：弹性模量E和泊松比v及控制塑性行为的3个参数：有效黏聚力c、有效内摩擦角和剪胀角。

MC模型采用了弹塑性理论，能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律，因而并不能较好地描述土体在破坏之前的变形行为，且不能考虑应力历史的影响及区分加荷和卸荷。

故MC模型能较好地模拟土体的强度问题，MC模型的六凌锥形屈服面（图2）与土样真三轴试验的应力组合形成的屈服面吻合得较好，因此MC模型适合于低坝、边坡等稳定性问题的分析。

➢Drucker -Prager（DP）模型DP模型对MC模型的屈服面函数作了适当的修改，采用圆锥形屈服面（图3）来代替MC模型的六凌锥屈服面，易于程序的编制和进行数值计算。

它存在与MC模型同样地缺点，相对而言，在模拟岩土材料时，MC模型较DP模型更加适合。

➢修正剑桥模型（MCC）MCC模型为等向硬化的弹塑性模型，它修正了剑桥模型的弹头形屈服面，采用帽子屈服面（椭圆形）（图4），以塑性体应变为硬化参数，能较好地描述黏性土在破坏之前的非线性和依赖于应力水平或应力路径的变形行为，MCC模型从理论上和试验上都较好地阐明了土体的弹塑性变形特征，是应用最为广泛的软土本构模型之一。

岩土类材料的弹塑性力学模型及本构方程摘要：本文主要结合岩土类材料的特性，开展研究其在受力变形过程中的弹性及塑性变形的特点，描述简化的力学模型特征及对应的适用条件，同时在分析研究其弹塑性力学模型的基础上，探究了关于岩土类介质材料的各种本构模型，如M-C、D-P、Cam、D-C、L-D及节理材料模型等，分析对应使用条件，特点及公式，从而推广到不同的材料本构模型的研究，为弹塑性理论更好的延伸发展做一定的参考性。

关键词：岩土类材料，弹塑性力学模型，本构方程不同的固体材料，力学性质各不相同。

即便是同一种固体材料，在不同的物理环境和受力状态中，所测得的反映其力学性质的应力应变曲线也各不相同。

尽管材料力学性质复杂多变，但仍是有规律可循的，也就是说可将各种反映材料力学性质的应力应变曲线，进行分析归类并加以总结，从而提出相应的变形体力学模型。

第一章岩土类材料地质工程或采掘工程中的岩土、煤炭、土壤，结构工程中的混凝土、石料，以及工业陶瓷等，将这些材料统称为岩土材料。

岩土塑性力学与传统塑性力学的区别在于岩土类材料和金属材料具有不同的力学特性。

岩土类材料是颗粒组成的多相体，而金属材料是人工形成的晶体材料。

正是由于不同的材料特性决定了岩土类材料和金属材料的不同性质。

归纳起来，岩土材料有3点基本特性：1.摩擦特性。

2.多相特性。

3.双强度特性。

另外岩土还有其特殊的力学性质：1.岩土的压硬性，2.岩土材料的等压屈服特性与剪胀性，3.岩土材料的硬化与软化特性。

4.土体的塑性变形依赖于应力路径。

对于岩土类等固体材料往往在受力变形的过程中，产生的弹性及塑性变形具备相应的特点，物体本身的结构以及所加外力的荷载、环境和温度等因素作用，常使得固体物体在变形过程中具备如下的特点。

固体材料弹性变形具有以下特点：(1)弹性变形是可逆的。

物体在变形过程中，外力所做的功以能量（应变能)的形式贮存在物体内，当卸载时，弹性应变能将全部释放出来，物体的变形得以完全恢复； (2)无论材料是处于单向应力状态，还是复杂应力状态，在线弹性变形阶段，应力和应变成线性比例关系；(3)对材料加载或卸载，其应力应变曲线路径相同。

岩土类材料的弹塑性力学模型及本构方程摘要：本文主要结合岩土类材料的特性，开展研究其在受力变形过程中的弹性及塑性变形的特点，描述简化的力学模型特征及对应的适用条件，同时在分析研究其弹塑性力学模型的基础上，探究了关于岩土类介质材料的各种本构模型，如M-C、D-P、Cam、D-C、L—D及节理材料模型等,分析对应使用条件，特点及公式,从而推广到不同的材料本构模型的研究，为弹塑性理论更好的延伸发展做一定的参考性。

关键词：岩土类材料，弹塑性力学模型，本构方程不同的固体材料，力学性质各不相同.即便是同一种固体材料，在不同的物理环境和受力状态中，所测得的反映其力学性质的应力应变曲线也各不相同。

尽管材料力学性质复杂多变，但仍是有规律可循的，也就是说可将各种反映材料力学性质的应力应变曲线，进行分析归类并加以总结，从而提出相应的变形体力学模型.第一章岩土类材料地质工程或采掘工程中的岩土、煤炭、土壤,结构工程中的混凝土、石料，以及工业陶瓷等，将这些材料统称为岩土材料。

岩土塑性力学与传统塑性力学的区别在于岩土类材料和金属材料具有不同的力学特性。

岩土类材料是颗粒组成的多相体，而金属材料是人工形成的晶体材料。

正是由于不同的材料特性决定了岩土类材料和金属材料的不同性质.归纳起来，岩土材料有3点基本特性：1.摩擦特性.2。

多相特性。

3.双强度特性。

另外岩土还有其特殊的力学性质:1。

岩土的压硬性，2.岩土材料的等压屈服特性与剪胀性,3.岩土材料的硬化与软化特性。

4.土体的塑性变形依赖于应力路径。

对于岩土类等固体材料往往在受力变形的过程中，产生的弹性及塑性变形具备相应的特点，物体本身的结构以及所加外力的荷载、环境和温度等因素作用,常使得固体物体在变形过程中具备如下的特点。

固体材料弹性变形具有以下特点：(1)弹性变形是可逆的.物体在变形过程中，外力所做的功以能量（应变能）的形式贮存在物体内，当卸载时，弹性应变能将全部释放出来，物体的变形得以完全恢复；（2)无论材料是处于单向应力状态，还是复杂应力状态，在线弹性变形阶段,应力和应变成线性比例关系；(3)对材料加载或卸载，其应力应变曲线路径相同。

岩土工程中的土体本构模型岩土工程是土木工程的重要分支，涉及到土壤和岩石的力学性质和工程应用。

土体本构模型是岩土工程中的一个重要内容，它描述了土体在力学应力下的变形和破坏特性。

本文将探讨岩土工程中的土体本构模型的基本概念、应用和发展趋势。

1. 土体本构模型的基本概念土体本构模型是描述土体力学性质的数学方程，它可以预测土体在受载时的应力应变关系。

本构模型通过考虑土体的物理和力学性质，将复杂的土体行为简化为一组数学方程。

常见的土体本构模型包括弹性模型、弹塑性模型、粘塑性模型等。

这些模型的选择取决于土体类型、应用场景和工程目的。

2. 土体本构模型在工程应用中的意义土体本构模型在岩土工程实践中具有重要的意义。

首先，它可以帮助工程师预测土体在给定荷载下的力学行为，从而指导工程设计和结构计算。

其次，本构模型可以用于评估不同土体材料及其组合的工程性能，为灾害防治、基础工程和地下结构的设计提供依据。

此外，本构模型还可用于优化工程方案、确定合理的土体参数、分析土体的稳定性和变形特性等。

3. 土体本构模型的发展趋势随着岩土工程的发展和研究的深入，土体本构模型也得到了不断的改进和扩展。

其中，主要的发展趋势有以下几个方面：3.1 多尺度力学模型传统的土体本构模型通常是基于宏观尺度的实验数据和现象观察，对于细观结构的影响不够准确。

近年来，研究者们开始关注多尺度土体力学模型的研究，通过考虑微观尺度的土体结构和介观尺度的物理机制，进一步提高土体本构模型的精度和可靠性。

3.2 加载历史效应的考虑土体在实际工程中受到的荷载通常是动态和变化的，而传统的土体本构模型往往只考虑静态荷载。

研究者们开始研究加载历史效应对土体行为的影响，并尝试将土体本构模型与土体的加载历史联系起来，从而更准确地预测土体的行为。

3.3 细粒土本构模型的改进细粒土是岩土工程中常见的一种土体类型，其特点是颗粒细小、颗粒间结构复杂。

传统的土体本构模型在描述细粒土的力学性质时存在一定的限制。

岩土工程中土体本构模型的研究与改进导言：岩土工程是土壤和岩石力学的应用学科，涉及地质工程、地下工程、堤坝工程等方面。

在岩土工程中，研究土体力学特性是非常重要的。

土体本构模型作为描述土体力学特性的数学模型，对于岩土工程的设计和分析具有重要意义。

本文将研究和改进在岩土工程中常用的土体本构模型，以提高工程设计的准确性和可靠性。

一、传统土体本构模型的局限性传统的土体本构模型常采用线性弹性模型或塑性模型进行描述，但这些模型在实际工程应用中存在一定的局限性。

首先，线性弹性模型忽略了土体在较大应力下的非线性变形特性。

其次，塑性模型在描述土体的变形特性时，仅考虑土体的体积塑性，但忽略了土体的剪切塑性，与实际工程情况存在一定的差距。

因此，需要对传统土体本构模型进行研究和改进，以提高模型的适用性和准确性。

二、复杂土体本构模型的研究与改进为了更好地描述土体的力学特性，研究人员提出了一系列复杂的土体本构模型。

这些模型在考虑土体的非线性特性、各向异性特性和剪切塑性特性的同时，还能够模拟土体在不同应力路径下的力学行为。

例如，Cam-Clay模型以及其改进版本，综合考虑了土体的体积变形、剪切变形和各向异性，适用于模拟粘土和软土的力学行为。

Hardening Soil模型则引入了孔隙压力的影响，并考虑了土体的强度衰减效应，适用于模拟岩土体在变动应力下的力学行为。

这些复杂的土体本构模型在改进了传统模型的同时，也增加了模型的复杂性和计算难度，需要更多的实验数据和计算技术支持。

三、新型土体本构模型的发展趋势随着计算机技术和数值方法的快速发展，越来越多的新型土体本构模型得到了研究和应用。

这些模型不仅考虑了传统模型所忽略的土体力学特性，还能够模拟土体在较大应力下的非线性变形，并提供更为准确的力学参数。

例如，基于塑性势函数理论的非线性本构模型，能够更好地描述土体在应力路径变化下的力学行为。

另外，细观尺度下的离散元模拟方法也为岩土工程提供了新的研究思路，通过将土体划分为离散的颗粒，并考虑颗粒间的作用力，模拟土体的宏观力学行为。

岩土类材料本构模型研究现状及发展趋势
岩土类材料本构模型的研究现状主要集中在以下几个方面：
1. 传统本构模型：目前岩土类材料常用的本构模型包括弹性模型、塑性模型和粘弹塑性模型等。

这些模型已经在岩土工程领域得到广泛应用，但仍存在一些不足之处，如无法精确描述材料的非线性行为、依赖于实验数据等。

2. 分子动力学模拟：近年来，随着计算机技术的发展，分子动力学模拟在岩土类材料本构模型研究中得到了广泛应用。

该方法基于分子尺度对材料的微观结构和性质进行研究，能够提供更准确的材料本构模型。

3. 非线性本构模型：针对岩土类材料的非线性行为，研究人员正在开发更精确的非线性本构模型。

这些模型能够考虑材料的强度、应变硬化、损伤以及温度等因素对材料行为的影响。

未来岩土类材料本构模型研究的发展趋势包括：
1. 多尺度本构模型：将不同尺度的模型进行耦合，从而提高模型的准确性和适用性。

例如，将分子动力学模拟结果与宏观本构模型相结合，以获得更准确的材料本构模型。

2. 数据驱动的本构模型：利用大数据和机器学习等技术，通过分析实验数据和观测数据来构建本构模型。

这种数据驱动的方法能够提高模型的预测能力和适用性。

3. 损伤模型：研究人员将更多注意力放在岩土材料的损伤行为研究上，以提高本构模型对材料失效的预测能力。

4. 特殊环境下的本构模型：考虑材料在特殊环境下的行为，如高温、低温、高压等条件下的应力应变关系。

总体来说，岩土类材料本构模型研究的发展趋势是朝着多尺度、数据驱动和考虑材料特殊环境影响的方向发展。

这将有助于提高模型的准确性和适用性，为岩土工程领域提供更科学、可靠的模型和方法。

土的本构模型综述1 土本构模型的研究内容土体是天然地质材料的历史产物。

土是一种复杂的多孔材料，在受到外部荷载作用后，其变形具有非线性、流变性、各向异性、剪胀性等特点。

为了更好地描述土体的真实力学—变形特性，建立其应力应变和时间的关系，在各种试验和工程实践经验的基础上提出一种数学模型，即为土体的本构关系。

自Roscoe等1958~1963年创建剑桥模型以来，各国学者相继提出了数百个土的本构模型，包括不考虑时间因素的线弹性模型、非线弹性模型、弹塑性模型和考虑时间因素的流变模型等。

本文将结合土本构模型的研究进程，综合分析已建立的经典本构模型，指出各种模型的优缺点和适用性，并对土本构模型的未来研究趋势进行展望。

2 土的本构模型的研究进程早期的土力学中的变形计算主要是基于线弹性理论的。

在线弹性模型中，只需两个材料常数即可描述其应力应变关系，即E和v或K和G或λ和μ。

其中邓肯张双曲线模型是研究最多、应用最广的非线弹性模型。

20世纪50年代末~60年代初，土塑性力学的发展为土的本构模型的研究开辟了一条新的途径。

Drucker等（1957年）提出在Mohr-Coulomb锥形屈服面上再加一组帽形屈服面，Roscoe等（1958年~1963年）建立了第一个土的本构模型——剑桥模型，标志着土的本构模型研究新阶段的开始。

70年代到80年代，计算机技术的迅速发展推动了非线性力学理论、数值计算方法和土工试验的发展，为在岩土工程中进行非线性、非弹性数值分析提供了可能性，各国学者提出了上百种土的本构模型，包括考虑多重屈服面的弹塑性本构模型和考虑土的变形及内部应力调整的时间效应的粘弹塑性模型。

此外，其他本构模型如土的结构性模型、内时本构模型等也是从不同角度描述土本构关系，有的学者则借用神经网络强大的自组织、自学习功能来反演土的本构关系。

3 几种经典的土本构模型3.1 Mohr-Coulomb(M-C)理想弹塑性模型Coulomb 在土的摩擦试验、压剪试验和三轴试验的基础上，于1773年提出了库仑破坏准则，即剪应力屈服准则，它认为当土体某平面上剪应力达到某一特定值时，就进入屈服。