软土本构模型综述课件
- 格式:doc
- 大小:108.00 KB
- 文档页数:10





![[PPT]土体本构模型的MARC实现及应用教学课件](https://uimg.taocdn.com/de6a052e852458fb760b561a.webp)

土的本构模型综述1 土本构模型的研究内容土体是天然地质材料的历史产物。
土是一种复杂的多孔材料,在受到外部荷载作用后,其变形具有非线性、流变性、各向异性、剪胀性等特点。
为了更好地描述土体的真实力学—变形特性,建立其应力应变和时间的关系,在各种试验和工程实践经验的基础上提出一种数学模型,即为土体的本构关系。
自Roscoe等1958~1963年创建剑桥模型以来,各国学者相继提出了数百个土的本构模型,包括不考虑时间因素的线弹性模型、非线弹性模型、弹塑性模型和考虑时间因素的流变模型等。
本文将结合土本构模型的研究进程,综合分析已建立的经典本构模型,指出各种模型的优缺点和适用性,并对土本构模型的未来研究趋势进行展望。
2 土的本构模型的研究进程早期的土力学中的变形计算主要是基于线弹性理论的。
在线弹性模型中,只需两个材料常数即可描述其应力应变关系,即E和v或K和G或λ和μ。
其中邓肯张双曲线模型是研究最多、应用最广的非线弹性模型。
20世纪50年代末~60年代初,土塑性力学的发展为土的本构模型的研究开辟了一条新的途径。
Drucker等(1957年)提出在Mohr-Coulomb锥形屈服面上再加一组帽形屈服面,Roscoe等(1958年~1963年)建立了第一个土的本构模型——剑桥模型,标志着土的本构模型研究新阶段的开始。
70年代到80年代,计算机技术的迅速发展推动了非线性力学理论、数值计算方法和土工试验的发展,为在岩土工程中进行非线性、非弹性数值分析提供了可能性,各国学者提出了上百种土的本构模型,包括考虑多重屈服面的弹塑性本构模型和考虑土的变形及内部应力调整的时间效应的粘弹塑性模型。
此外,其他本构模型如土的结构性模型、内时本构模型等也是从不同角度描述土本构关系,有的学者则借用神经网络强大的自组织、自学习功能来反演土的本构关系。
3 几种经典的土本构模型3.1 Mohr-Coulomb(M-C)理想弹塑性模型Coulomb 在土的摩擦试验、压剪试验和三轴试验的基础上,于1773年提出了库仑破坏准则,即剪应力屈服准则,它认为当土体某平面上剪应力达到某一特定值时,就进入屈服。

第29卷 第4期 岩 土 工 程 学 报 Vol.29 No.4 2007年 4月 Chinese Journal of Geotechnical Engineering Apr., 2007 K0固结结构性软黏土的本构模型王立忠,沈恺伦(浙江大学建筑工程学院,浙江 杭州 310027)摘 要:本文在修正剑桥模型的基础上综合考虑了软黏土的各向异性、结构性及其演变和屈服面硬化规则中塑性剪切应变的影响,将传统模型发展为适用于K0固结结构性软黏土的本构模型。
本文模型借鉴Collins等人提出的符合热力学耗散原理的本构模型,同时在描述土体结构性演变的过程中参考了Asaoka等人的次加载/超加载屈服面本构模型,并采用了具有明确物理意义的内变量。
与传统的修正剑桥模型相比,增加了3个分别表征软黏土各向异性和结构性的参数(θn,R和R*)以及两个演化参数(m和a),而参数R和R*的初始值则可由结构性土的屈服应力比YSR和灵敏度S t获得。
本文选取了典型的浙江温州软黏土和Bothkennar软黏土,对比了三轴压缩的计算和试验结果,体现了本模型在结构性软黏土计算上相对于传统本构模型优越性。
关键词:软黏土;结构性;K0固结;各向异性中图分类号:TD853.34文献标识码:A 文章编号:1000–4548(2007)04–0496–09作者简介:王立忠(1969–),男,浙江奉化人,教授,博士生导师,从事软黏土力学和土动力学的研究。
E-mail:wlzzju@。
A constitutive model of K0 consolided structured soft claysWANG Li-zhong,SHEN Kai-lun(College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310027, China)Abstract:A constitutive model of K0 consolided structured soft clays was developed based on the Modified Cam Clay model.The effects of anisotropy and destructuration of the natural soils as well as shear hardening rule were considered with the rotational yield surface. This model came from the thermo-mechanical constitutive model developed by Collins and then the methods that Asaoka established in the super/subloading yield surface model were used. Three parameters (θn, R and R*) and two evolution parameters (m and a) were added to the Modified Cam Clay model together with the initial structural values which were related to the yield stress ratio and the sensitivity of the soft clays. Significant improvements were demonstrated in the performance of the new model over the traditional constitutive models with experimental evidence from Wenzhou clay and Bothkennar clay.Key words:soft clay; structure; K0 consolidation; anisotropy0 前 言剑桥模型和修正剑桥模型在各向同性的软土地基工程计算中得到普遍应用。

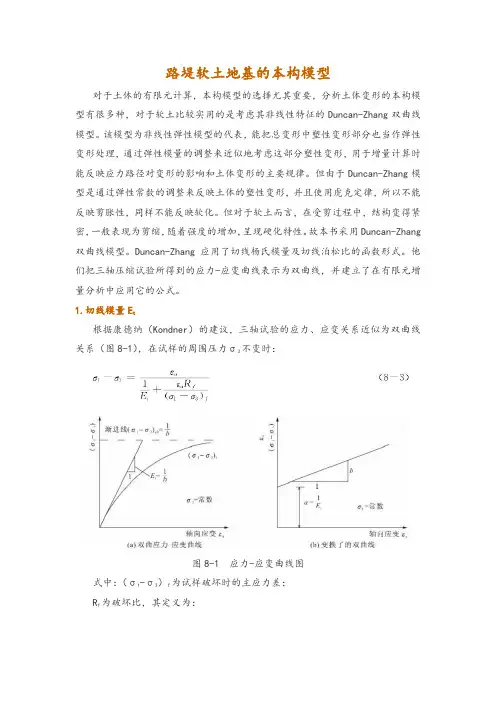
路堤软土地基的本构模型对于土体的有限元计算,本构模型的选择尤其重要,分析土体变形的本构模型有很多种,对于软土比较实用的是考虑其非线性特征的Duncan-Zhang双曲线模型。
该模型为非线性弹性模型的代表,能把总变形中塑性变形部分也当作弹性变形处理,通过弹性模量的调整来近似地考虑这部分塑性变形,用于增量计算时能反映应力路径对变形的影响和土体变形的主要规律。
但由于Duncan-Zhang模型是通过弹性常数的调整来反映土体的塑性变形,并且使用虎克定律,所以不能反映剪胀性,同样不能反映软化。
但对于软土而言,在受剪过程中,结构变得紧密,一般表现为剪缩,随着强度的增加,呈现硬化特性。
故本书采用Duncan-Zhang 双曲线模型。
Duncan-Zhang应用了切线杨氏模量及切线泊松比的函数形式。
他们把三轴压缩试验所得到的应力-应变曲线表示为双曲线,并建立了在有限元增量分析中应用它的公式。
1.切线模量Et根据康德纳(Kondner)的建议,三轴试验的应力、应变关系近似为双曲线关系(图8-1),在试样的周围压力σ3不变时:图8-1 应力-应变曲线图式中:(σ1-σ3)f为试样破坏时的主应力差;Rf为破坏比,其定义为:式(8-3)对轴应变εa求导数,得到在曲线上任一点的切线模量为:图8-2 初始切线模量与固结压力关系图式(8-3)可改写为:由以上两式得到:根据简布(Janbu)的研究,初始切线模量Ei 与固结压力σ3的关系可表示为:式中:K、n为由试验确定的参数,由Ei 与σ3的关系求得(图8-2);P a 为大气压力,单位与Ei相同,引入它以使K成为无量纲的数。
根据莫尔-库仑屈服准则得:式中:c、φ为土的凝聚力和内摩擦角。
将式(8-8)、式(8-9)代入式(8-7),得到了以下切线模量表达式:2.切线泊松比μt切线泊松比μt的表达式是库哈维(Kulhawy)等采用与推导切线模量相似的方法得到的。
、c、φ、F、G、D都是由式(8-10)、式(8-11)共8个参数,即K、n、Rf三轴试验确定的。

《软土地基》课程论文学院建工学院姓名王洋学号软土本构模型综述1 引言土体具有复杂的变形特征,如剪胀性、各向异性、受应力路径影响等。
土体变形的这种复杂性是在复杂受力状态下表现出来的。
复杂应力状态存在 6 个应力分量,也有 6 个应变分量。
其间的关系是一种多因素物理量与多因素物理量之间的关系,不能由试验直接建立。
须在简化条件的试验基础上,做某些假定及合乎规律的推理,从而提出某种计算方法,把应力应变关系推广到复杂应力状态。
这种计算方法叫本构模型。
1.1 土的本构模型发展到现在,土的本构模型数目众多,大致可以分为以下几大类: ( 1) 非线性模型;( 2) 弹塑性模型;( 3) 粘弹塑性模型;( 4) 结构性模型。
对于软土而言,比较适用的一般为弹塑性模型。
弹塑性模型是把总的变形分成弹性变形和塑性变形两部分,用虎克定律计算弹性变形部分,用塑性理论来解塑性变形部分。
1.2 变形假定对于塑性变形,要作三方面的假定:( 1) 破坏准则和屈服准则;( 2) 硬化准则;( 3) 流动法则。
不同的弹塑性模型,这三个假定的具体形式也不同。
最常用的弹塑性模型为剑桥模型及其扩展模型。
2 剑桥模型与修正剑桥模型1958 年,Roscoe 等发现了散粒体材料在孔隙比-平均有效应力-剪应力的三维空间里存在状态面的事实,1963 年,提出了著名的剑桥模型,1968 年,形成了以状态面理论为基础的剑桥模型的完整理论体系。
Roscoe 等人将“帽子”屈服准则、正交流动准则和加工硬化规律系统地应用于Cam 模型之中,并提出了临界状态线、状态边界面、弹性墙等一系列物理概念,构成了第一个比较完整的土塑性模型。
剑桥模型又被称为临界状态模型,是一个非常经典的弹塑性模型,它是第一个全面考虑重塑正常固结或弱超固结粘土的压硬性和剪胀性的模型,标志着土的本构理论发展新阶段的开始。
1968 年,Roscoe 等人在剑桥模型的基础上提出了修正剑桥模型,将原来的屈服面在p',q 平面上修正为椭圆,并认为在状态边界面内土体变形是完全弹性的。
在状态边界面内,增加的剪应力虽不产生塑性体积变形,但可产生塑性剪切变形。
修正剑桥模型是一种“帽子”型模型,在许多情况下能更好地反映土的变形特性。
修正剑桥模型至今仍在工程中广泛应用,是因为它具有很多优点: 形式简单,模型参数少,参数确定方法简单( 只需常规三轴试验即可) ,参数有明确的物理意义,能够很好的反映重塑正常固结或弱超固结粘土的压硬性和剪缩性,因此修正剑桥模型是土力学中比较成熟而且应用广泛的弹塑性本构模型。
同时,修正剑桥模型也有一定的局限性: 屈服面只是塑性体积应变的等值面,只采用塑性体积应变作硬化参量,因而没有充分考虑剪切变形; 只能反映土体剪缩,不能反映土体剪胀; 没有考虑土的结构性这一根本内在因素的影响; 假定的弹性墙内加载仍会产生塑性变形等。
修正剑桥模型对实际情况进行了一系列假定:①屈服只与应力球量p 和应力偏量q 两个应力分量有关,与第三应力不变量无关; ②采用塑性体应变硬化规律,以为硬化参数; ③假定塑性变形符合相关联的流动法则,即g( σ) = f( σ) ; ④假定变形消耗的功,即塑性功为:剑桥模型是当前在土力学领域内应用最广的模型之一,其主要特点有: 基本概念明确; 较好地适宜于正常固结粘土和弱超固结粘土; 仅有3个参数,都可以通过常规三轴试验求出,在岩土工程实际工作中便于推广; 考虑了岩土材料静水压力屈服特性、剪缩性和压硬性。
王清等分析了修正剑桥模型的应力应变关系,以其为基础引进了接触单元和杆单元,运用修正合格模型,用有限元程序模拟了工程实例中的开挖过程和开挖要素,模拟计算了不同开挖阶段的地表沉降、基坑隆起和水平位移,根据计算结果与实测结果的比较,验证了在软土地区此模型是适用的,此外,王清等人还对基坑开挖施工、地面沉降预测作了定性分析。
3 岩土模型的发展岩土模型的发展大致可归为以下几类:( 1) 基于经典塑性理论框架的修正。
( 2) 非关联流动准则的引用; 由于关联流动准则要求塑性势函数和屈服函数一致,给寻找和选取符合条件的屈服函数带来了很大困难,而非关联流动准则将二者区分开来,从而带来更多选择的余地,可以通过试验较为容易地确定屈服函数,所以随后发展出了很多基于非关联流动准则的本构模型。
( 3) 亚塑性理论与临界状态理论相结合。
亚塑性理论以有理力学为理论基础,扬弃了经典弹塑性理论中总应变分解为弹性应变和塑性应变、屈服准则、硬化规律、塑性势及流动法则等基本概念和假设,直接建立起联系应变率空间与应力率空间的各向同性非线性张量函数表达式,从整体上表述砂等无黏性散粒型土体的应力-应变关系。
( 4) 考虑有限应变,使模型摆脱了传统的小应变假设,将分析范围从仅适于小应变扩展到亦适用于有限应变,从而在计算假设上更接近于岩土问题的实际情况( 即岩土问题的大变形) ,使岩土数值计算工作变得更加有实际意义。
( 5) 考虑土的时间相关性。
即把时间相关因素加入粘土应力-应变关系中,从而把总变形分为瞬时应变和粘性应变部分,得到了时间相关粘土模型。
( 6) 考虑土的各向异性及结构性。
( 7) 模拟土在循环荷载下特性。
( 8) 推广到一般三维应力空间。
( 9) 将本构扩展到砂土、非饱和土。
4 剑桥模型的发展近年来,针对这种模型进行了不同方面的改进或扩展。
Dimaggi 等在剑桥模型的基础上提出了帽盖模型。
该模型不仅能描述塑性屈服前的非线性、剪胀性等特性,还能描述屈服后的各种破坏性状与塑性硬化性状。
魏汝龙根据不排水三轴压缩试验资料得到了正常固结粘土模型,比修正剑桥模型具有更大的适应性,修正剑桥模型仅是它的特例。
Banerjee 等基于剑桥模型框架,采用塑性增量理论,分析各向同性正常固结及微超固结粘土的不排水应力应变反映,建立了关联和非关联流动的弹塑性本构模型。
Masin将次塑性理论与临界状态土力学相结合,建立了一个既适用于正常固结也适用于超固结粘土的本构模型。
孙德安等改进了修正剑桥模型的屈服面形状,提出了一种介于剑桥模型和关口-太田模型两者之间、考虑初始应力各向异性的不等向塑性体变硬化弹塑性模型。
此模型考虑应力Lode 角和初始各向异性应力状态的影响,从而反映三维应力状态下土的变形和强度特性,还有考虑长期荷载或循环荷载作用下多种应力路径的影响,从而反映土的蠕变效应以及循环变形特性等。
为了使模型在三维应力下较好地反映土的强度和变形特性,模型的剪切屈服准则使用SMP 准则。
模型的土性参数与剑桥模型一样,其预测值与粘土实测值的比较表明,提出的模型是简单合理的。
徐连民等进一步尝试用最新三维修正剑桥模型研究超固结土的变形和强度特性,将土的超固结比引入到修正剑桥模型中,将超固结比作为屈服函数的一个状态量,再通过这个状态量的演化来反映超固结土的变形和强度特性的变化规律。
经过这样扩展后的三维修正剑桥模型不仅可以模拟正常固结土的体积剪缩特性,而且还可以模拟三轴压缩和伸长条件下超固结土的体积剪胀特性,而本构模型仅增加一个和超固结比有关的材料参数。
最后,采用超固结比OCR ( Over Consolidated Ratio) 分别等于1、2、4、8 的藤森黏土在平均有效应力一定条件下的三轴压缩和伸长试验结果验证了三维修正剑桥模型在各种应力路径下对超固结黏土的变形和强度预测能力。
Wu 等( 1996) 等提出了一个基于临界状态理论的亚塑性理论本构模型,用以描述粒状材料的三维非线性应力应变关系以及体积剪胀特性; Masin 等( 2005)研究了近期提出的粘土亚塑性模型的数学方程,主要研究了亚塑性模型对状态边界面( state boundary surface) 的预测问题,随后提出了一个新的基于修正剑桥模型和松岗中井破坏面的粘土亚塑性本构模型; 2007年,Masin又提出了一个针对亚稳结构粘土( clays with metastable structure) 的亚塑性本构模型。
Yatomi 等提出了考虑有限应变的剑桥模型,并加入了非共轴因素,使模型能够模拟土的局部剪切带; Callari 等,Borja 等也分别建立了有限应变剑桥本构模型,Ortiz 等建立了基于剑桥模型的非粘性土本构模型,使模型使用范围从小应变扩展到有限应变。
Hsieh 等利用剑桥塑性理论把时间相关因素加入粘土应力-应变关系中,从而把总变形分为瞬时应变和粘性应变部分,得到了一个时间相关粘土模型; Arai 等结合剑桥模型建立了时间相关的正常固结粘土塑性模型,并且考虑了粘土各向异性固结对其应力-应变关系的影响; Yin 等基于修正剑桥模型建立了一个能够模拟加速蠕变、卸荷再加载、应力松弛等软粘土变形行为的弹粘塑本构模型。
Dafafias 等在临界状态土力学框架内建立了一个各向异性粘土塑性本构模型,加入了非关联流动准则,以便成功模拟正常固结粘土不排水加载下特性; 魏星等先后建立了软土初始应力各向异性弹塑性模型,软黏土的各向异性临界状态模型和天然结构性黏土的各向异性边界面模型; Zhang 等推导了一个应力诱导各向异性弹塑性模型,通过引入应力诱导各向异性的概念,结合新的超固结比的发展准则,统一地描述了土在循环荷载下的力学特性,包括中密砂及粘土的循环移动性; Rouainia 等在边界面塑性为基础的运动硬化理论框架下提出了一个天然粘土的率相关本构模型,以表现不可回复塑性应变对土体结构性的破坏。
Li 等在临界状态土力学和新型运动硬化的基础上提出了一个双面模型,用以预测饱和粘性土循环荷载下的不排水特性; McDowell 等提出了一个有3个屈服面的运动硬化模型( 3-SKH 模型) ,该模型可以考虑动力问题,即可以模拟土在循环荷载下的特性。
随后,二人又于2004年对此模型进行了简化,以推广其应用; Jastrzebska 等提出了一个描述循环荷载下粘性土特性的模型( NAHOS) 。
Ling 等基于临界状态概念,应用一个状态参量,提出了一个针对砂土的一元化通用塑性模型。
该模型使用了非线性临界状态线,可以模拟排水和不排水条件下不同密度砂土在不同压力水平下的应力-位移特性。
Yu 等提出了一个能够模拟排水和不排水条件下砂土和粘土循环荷载下的应力应变特性的模型( CASM-c)。
这个模型建立在一元化临界状态模型CASM ( Yu,1995,1998) 上,新加入了边界面塑性理论,在计算再加载和卸载硬化模量时使用了不同的方法。
近年来,Sloan 等等提出了能够控制误差的显式积分算法,并与时间步长的自动划分方法相结合,比较有效地改善了显式积分算法的精度。
作为本构模型的另一类积分算法,基于广义梯形积分算法或广义中心积分算法的隐式积分算法,可以通过平衡迭代保证应力状态始终位于当前屈服面,具有非常高的计算精度。