2016年北京市朝阳区高三理科数学期末试题及答案

北京市朝阳区2015-2016学年度第二学期高三综合练习（二）数学（理科）2016．5一、选择题：本大题共8小题，每小题5分，共40分．在四个选项中，选出符合题目要求的一项．1．已知集合{}124xA x =<<，{}10B x x =-≥，则A B I ＝（ ）A ．{}12x x ≤< B ．{}01x x <≤C ．{}01x x <<D ．{}12x x <<2．复数i1iz =-（i 为虚数单位）在复平面内对应的点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．执行如图所示的程序框图，输出的S 值为（ ） A ．6B ．10C ．14D ．154．已知非零向量a ，b ，“a ∥b ”是“a ∥()+a b ”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件5．同时具有性质:“①最小正周期是π； ②图象关于直线3x =π对称；③在区间56⎡⎤⎢⎥⎣⎦，ππ上是单调递增函数”的一个函数可以是（ ） A ．cos 26x y ⎛⎫=+⎪⎝⎭π B ．sin 26y x 5⎛⎫=+⎪⎝⎭π C ．cos 23y x ⎛⎫=-⎪⎝⎭π D ．sin 26y x ⎛⎫=-⎪⎝⎭π 6．已知函数()122log 2a x x f x x x -≤⎧=⎨+>⎩，，(0a >且)1a ≠的最大值为1，则a 的取值范围是（ ）A ．112⎡⎫⎪⎢⎣⎭，B ．()01，C ．102⎛⎤ ⎥⎝⎦，D ．()1+∞，7．某学校高三年级有两个文科班，四个理科班，现每个班指定1人，对各班的卫生进行检查．若每班只安排一人检查，且文科班学生不检查文科班，理科班学生不检查自己所在的班，则不同安排方法的种数是（ ） A ．48B ．72C ．84D ．1688．已知正方体1111ABCD A BC D -的棱长为2，E 是棱11D C 的中点，点F 在正方体内部或正方体的表面上，且EF ∥平面11A BC ，则动点F 的轨迹所形成的区域面积是（ ）A．92B．C ．D ．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．双曲线22:13x C y -=的渐近线方程是 ；若抛物线()220y px p =>的焦点与双曲线C 的一个焦点重合，则p = ．10．如图，P 为⊙O 外一点，PA 是⊙O 的切线，A 为切点，割线PBC 与⊙O 相交于B C ，两点，且3PC PA =，D 为线段BC 的中点，AD 的延长线交⊙O 于点E ．若1PB =，则PA 的长为______；AD DE ⋅的值是 ．11．已知等边ABC ∆的边长为3，D 是BC 边上一点，若1BD =，则AC AD ⋅uu u r uuu r的值是______．12．已知关于x y ，的不等式组022x y x x y x y k≥⎧⎪≥⎪⎨+≤⎪⎪-≥⎩所表示的平面区域D 为三角形区域，则实数k 的取值范围是 ．13．为了响应政府推进“菜篮子”工程建设的号召，某经销商投资60万元建了一个蔬菜生产基地.第一年支出各种费用8万元，以后每年支出的费用比上一年多2万元.每年销售蔬菜的收入为26万元.设()f n 表示前n 年的纯利润（()f n =前n 年的总收入－前n 年的总费用支出－投资额），则()f n = （用n 表示）；从第______年开始盈利.14．在平面直角坐标系xOy 中，以点A ()20， ，曲线y =B ，第一象限内的点C ，构成等腰直角三角形ABC ，且90A ∠=︒，则线段OC 长的最大值是______．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）在ABC ∆中，角A ，B ，C 的对边分别是a ，b ，c ，sin A C =． （Ⅰ）求a 的值；（Ⅱ）若角A 为锐角，求b 的值及ABC ∆的面积．交通指数值0.25 0.10 0.050.15 02 4 6 8 10 0.20 13 5 7 9 交通指数是交通拥堵指数的简称，是综合反映某区域道路网在某特定时段内畅通或拥堵实际情况的概念性指数值．交通指数范围为()010， ，五个级别规定如下：某人在工作日上班出行每次经过的路段都在同一个区域内，他随机记录了上班的40个工作日早高峰时段（早晨7点至9点）的交通指数（）平均值），其统计结果如直方图所示． （Ⅰ）据此估计此人260个工作日中早高峰时段（早晨7点至9点）中度拥堵的天数；（Ⅱ）若此人早晨上班路上所用时间近似为：畅通时30分钟，基本畅通时35分钟，轻度拥堵时40分钟，中度拥堵时50分钟，严重拥堵时70分钟，以直方图中各种路况的频率作为每天遇到此种路况的概率，求此人上班路上所用时间X 的数学期望．ECDBA图1BFOCDA 1E 图2如图1，在等腰梯形ABCD 中，//BC AD ，122BC AD ==，60A ∠=︒，E 为AD 中点，点O F 、分别为,BE DE 的中点．将ABE ∆沿BE 折起到1A BE ∆的位置，使得平面1A BE ⊥平面BCDE （如图2）． （Ⅰ）求证：1AO CE ⊥； （Ⅱ）求直线1A B 与平面1ACE 所成角的正弦值； （Ⅲ）侧棱1AC 上是否存在点P ，使得//BP 平面1AOF ？若存在，求出11A PAC 的值；若不存在，请说明理由．已知函数()()()2111ln 2f x x a x a x =-+++-，a R ∈． （Ⅰ）当3a =时，求曲线():C y f x =在点()()11f ，处的切线方程； （Ⅱ）当[]12x ∈， 时，若曲线():C y f x =上的点()x y ，都在不等式组1232x x y y x ⎧⎪≤≤⎪≤⎨⎪⎪≤+⎩所表示的平面区域内，试求a 的取值范围．19．（本小题满分14分）在平面直角坐标系xOy 中，点()()0000P x y y ≠，在椭圆22:12x C y +=上，过点P 的直线l 的方程为0012x xy y +=． （Ⅰ）求椭圆C 的离心率；（Ⅱ）若直线l 与x 轴、y 轴分别相交于A B 、两点，试求OAB ∆面积的最小值；（Ⅲ）设椭圆C 的左、右焦点分别为1F ，2F ，点Q 与点1F 关于直线l 对称，求证：点2Q P F 、、三点共线．20．（本小题满分13分）已知集合(31122n S k k k N n *⎧⎫-⎪⎪=≤≤∈≥⎨⎬⎪⎪⎩⎭，，且)n N *∈．若存在非空集合12n S S S ，，，，使得12n S S S S =，且()1i j S S i j n i j =∅≤≤≠，，，并()12i x y S i n x y ∀∈=>，， ，，，，都有i x y S -∉，则称集合S 具有性质P ，i S （12i n =， ，，）称为集合S 的P 子集． （Ⅰ）当2n =时，试说明集合S 具有性质P ，并写出相应的P 子集12S S ，；（Ⅱ）若集合S 具有性质P ，集合T 是集合S 的一个P 子集，设{}3nT s s T '=+∈，求证：x y T T '∀∈，，x y >，都有x y TT '-∉；（Ⅲ）求证：对任意正整数2n ≥，集合S 具有性质P ．北京市朝阳区2015-2016学年度第二学期高三年级统一考试数学答案（理工类） 2016．5一、选择题：（满分40分）二、填空题：（满分30分） [0,1)（注：两空的填空，第一空3分，第二空2分） 三、解答题：（满分80分） 15．（本小题满分13分）解：（）Ⅰ） 0A <<π，由正弦定理sin sin a cA C=…………………6分（）Ⅱ） cos A =由余弦定理2222cos a b c bc A =+-，得22150b b --=． 解得5b =或3b =-（舍负）．…………………13分 解: （Ⅰ）由已知可得：上班的40个工作日中早高峰时段中度拥堵的频率为0.25， 据此估计此人260个工作日早高峰时段（早晨7点至9点）中度拥堵的天数为 260×0.25=65天. ……………………………………………………5分 （Ⅱ）由题意可知X 的可能取值为30,35,40,50,70．且(30)0.05P X ==；(35)0.10P X ==；(40)0.45P X ==； (50)0.25P X ==；(70)0.15P X ==；所以300.05+350.1+400.45+500.25+700.15=46EX =⨯⨯⨯⨯⨯．…………………………………13分17．（本小题满分14分）解：（Ⅰ）如图1，在等腰梯形ABCD 中，由//BC AD ，122BC AD ==，60A ∠=︒，E 为AD 中点，所以ABE ∆为等边三角形．如图2, 因为O 为BE 的中点，所以1AO BE ⊥． 又因为平面1A BE ⊥平面BCDE ， 且平面1A BE平面BCDE BE =，所以1AO ⊥平面BCDE ，所以1AO CE ⊥．………4分 （Ⅱ）连结OC ，由已知得CB CE =，又O 为BE 的中点，图2所以OC BE ⊥．由（Ⅰ）知1AO ⊥平面BCDE ， 所以11,AO BE AO OC ⊥⊥， 所以1,,OA OB OC 两两垂直．以O 为原点，1,,OB OC OA 分别为,,x y z 轴建立空间直角坐标系（如图）．因为2BC =，易知1OA OC ==所以1(00(100),(0(100)A B C E -，，，，，所以111(103),(033),(10A B AC A E =-=-=-，，，，，． 设平面1ACE 的一个法向量为(,,)x y z =n ， ECDBA图1DCBFODA 1E由 110,0 AC A E ⎧⋅=⎪⎨⋅=⎪⎩n n得0, 0.x -=--=⎪⎩即0, 0. y z x -=⎧⎪⎨+=⎪⎩取1z =，得(,1)=n ． 设直线1A B 与平面1ACE 所成角为θ，则1sin cos ,A B θ=〈〉===n ． 所以直线1A B 与平面1ACE 所成角的正弦值为5． …………………9分 （Ⅲ）假设在侧棱1AC 上存在点P ，使得//BP 平面1AOF ． 设11A P AC λ=，[0,1]λ∈．因为1111BP BA A P BA AC λ=+=+，所以(10(0(1)BP λ=-+=-． 易证四边形BCDE 为菱形，且CE BD ⊥，又由（Ⅰ）可知，1AO CE ⊥，所以CE ⊥平面1AOF ．所以(1,CE =-为平面1AOF 的一个法向量．由(1)(1,130BP CE λ⋅=-⋅-=-=，得1[0,1]3λ=∈． 所以侧棱1AC 上存在点P ，使得//BP 平面1AOF ，且1113A P AC =． …………14分 18．（本小题满分13分） 解：（Ⅰ）当3a =时, 21()42ln 2f x x x x =-+-，0x >． 2()4f x x x'=-+-． 则(1)1421f '=-+-=，而17(1)422f =-+=． 所以曲线在点（1,(1)f ）处的切线方程为712y x -=-，即2250x y -+=．…………………………………………………………………………4分C（Ⅱ）依题意当时，曲线上的点都在不等式组12,,32x x y y x ⎧⎪≤≤⎪≤⎨⎪⎪≤+⎩所表示的平面区域内，等价于当时，3()2x f x x ≤≤+恒成立． 设211)ln 2x ax a x （=-++-，． 所以21(1)()=+=a x ax a g x x a+x x---++-'(1)(1))=x x a x ---(-．（1）当11a -≤，即2a ≤时，当[]1,2x ∈时，()0g x '≤，()g x 为单调减函数，所以(2)()(1)g g x g ≤≤． 依题意应有131,222221ln20,()()()g a g a a ⎧=-≤⎪⎨⎪=-++-≥⎩ 解得21a a ,.≤⎧⎨≥⎩所以12a ≤≤．（2）若 112a <-<，即23a <<时，当[)1,1x a ∈-，()0g x '≥，()g x 为单调增函数，当x ∈(]1,2a -，()0g x '<，()g x 为单调减函数．由于13(1)(1)22g a g a ->=->，又因为max 3()(1)2g x g a =-≤，矛盾，所以不合题意． （3）当12a -≥，即3a ≥时，注意到max 15()(2)(1)22g x g g a =>=-≥，又因为max 3()(2)2g x g =≤，矛盾，显然不合题意．综上所述，12a ≤≤． …………………………………………13分19．（本小题满分14分） 解：（Ⅰ）依题意可知a =1c ==，所以椭圆C离心率为e ==． …………… 3分 （Ⅱ）因为直线l 与x 轴，y 轴分别相交于,A B 两点，所以000,0x y ≠≠． 令0y =，由0012x x y y +=得02x x =，则02(,0)A x ． []1,2x ∈C (),x y 12x ≤≤()()g x f x x =-[]1,2x ∈令0x =，由0012x x y y +=得01y y =，则01(0,)B y ． 所以OAB ∆的面积0000112122OAB S OA OB x y x y ∆===． 因为点00(,)P x y 在椭圆:C 2212x y +=上，所以220012x y +=．所以220012x y =+≥．即00x y ≤，则001x y ≥所以00112OAB S OA OB x y ∆==≥． 当且仅当22002x y =，即001,2x y =±=±时，OAB ∆… 9分 （Ⅲ）①当00x =时，(0,1)P ±．当直线:1l y =时，易得(1,2)Q -，此时21F P k =-，21F Q k =-．因为22F Q F P k k =，所以三点2,,Q P F 共线． 同理，当直线:1l y =-时，三点2,,Q P F 共线．②当00x ≠时，设点(,)Q m n ，因为点Q 与点1F 关于直线l 对称，所以000011,22202() 1.1212x m n y n x m y -⎧⋅+⋅=⎪⎪⎪⎨-⎪⋅-=--⎪+⎪⎩整理得000000240,220.x m y n x y m x n y +--=⎧⎨-+=⎩解得220002200000220044,448.4x x y m y x x y y n y x ⎧+-=⎪+⎪⎨+⎪=⎪+⎩所以点22000000222200004448(,)44x x y x y y Q y x y x +-+++． 又因为200(1,)F P x y =-，220000002222200004448(1,)44x x y x y y F Q y x y x +-+=-++， 且22200000000000002222220000004448(48)(48)(1)(1)(1)444x x y x y y x y x x y x y y x y x y x +-+--+--⋅-⋅-=⋅+++2200000220048(448)4x y x x y y x --+-=⋅+ 222200000002222220000008484(2)84280444y x y x y y y y x y x y x --+-++-⨯+=⋅=⋅=⋅=+++． 所以2//F P 2F Q ．所以点2,,Q P F 三点共线．综上所述，点2,,Q P F 三点共线． …………………………………14分 20．（本小题满分13分）证明：（Ⅰ）当2n =时，{1,2,3,4}S =，令1{1,4}S =，2{2,3}S =,则12S S S =, 且对,(1,2),i x y S i x y ∀∈=>，都有i x y S -∉，所以S 具有性质P ．相应的P 子集为1{1,4}S =，2{2,3}S =． ………… 3分（Ⅱ）①若31,(1)2n x y T y x -∈≤<≤,由已知x y T -∉, 又31132n n x y --≤-<,所以x y T '-∉．所以'x y T T -∉．②若,x y T '∈,可设3,3nnx s y r =+=+，,r s T ∈,且3112n r s -≤<≤，此时31(3)(3)132n nnn x y s r s r --=+-+=-≤-<．所以'x y T -∉，且x y s r T -=-∉．所以x y T T '-∉．③若y T ∈, 3nx s T '=+∈,s T ∈，则313331(3)()3(1)3222n n n nnnx y s y s y -+--=+-=-+≥-+=>, 所以x y T -∉．又因为,y T s T ∈∈，所以s y T -∉．所以(3)()3nnx y s y s y T '-=+-=-+∉． 所以'x y TT -∉．综上，对于,'x y T T ∀∈，x y >，都有'x y T T -∉． …………… 8分（Ⅲ）用数学归纳法证明．（1）由（Ⅰ）可知当2n =时，命题成立，即集合S 具有性质P ． （2）假设n k =（）2k ≥）时，命题成立．即1231{1,2,3,,}2k k S S S S -==，且(1,,)ij S S i j n i j =∅≤≤≠，,(1,2,,),i x y S i k x y ∀∈=>，都有i x y S -∉．那么 当1n k =+时，记{3|}ki i S s s S '=+∈,，并构造如下个集合：111S S S '''=,222S S S '''=,,k k kS S S '''=， 1313131{1,2,,21}222k k k k S +---''=++⨯+，显然()i j S S i j ''''=∅≠．又因为131313122k k +--=⨯+，所以112131{1,2,3,,}2k kk S S S S ++-''''''''=．下面证明中任意两个元素之差不等于中的任一元素(1,2,,1)i k =+．①若两个元素13131,22k k k r s S +--''++∈,31112k r s -≤<≤+, 则313131()()222k k k s r s r ---+-+=-≤, 所以13131()()22k k k s r S +--''+-+∉． ②若两个元素都属于i ii S S S '''=(1)i k ≤≤,由（Ⅱ）可知，i S ''中任意两个元素之差不等于i S ''中的任一数(1,2,,1)i k =+．从而，1n k =+时命题成立．综上所述，对任意正整数2n ≥，集合S 具有性质P ．………………………13分k +1 ¢¢S i¢¢S i。

数学答案（理工类） 2016．5一、选择题：（满分40分） 题号1 2 3 4 5 6 7 8 答案 A B B C D A D C二、填空题：（满分30分） 题号9 10 11 12 13 14 答案 33y x =±，4 3，16 6 (,2][0,1)-∞- 21960n n -+-,5 221+ （注：两空的填空，第一空3分，第二空2分）三、解答题：（满分80分）15．（本小题满分13分）解：(Ⅰ) 因为21cos 212sin 3A A =-=-，且 0A <<π， 所以6sin 3A =． 因为3,sin 6sin c A C ==，由正弦定理sin sin a c A C=，得66332a c =⋅=⨯=．…………………6分 (Ⅱ) 由6sin ,032A A π=<<得3cos 3A =． 由余弦定理2222cos a b c bc A =+-，得22150b b --=．解得5b =或3b =-（舍负）．所以152sin 22ABC S bc A ∆==． …………………13分 解: （Ⅰ）由已知可得：上班的40个工作日中早高峰时段中度拥堵的频率为0.25，据此估计此人260个工作日早高峰时段（早晨7点至9点）中度拥堵的天数为260×0.25=65天. ……………………………………………………5分（Ⅱ）由题意可知X 的可能取值为30,35,40,50,70．且(30)0.05P X ==；(35)0.10P X ==；(40)0.45P X ==；(50)0.25P X ==；(70)0.15P X ==；所以300.05+350.1+400.45+500.25+700.15=46EX =⨯⨯⨯⨯⨯．…………………………………13分17．（本小题满分14分）解：（Ⅰ）如图1，在等腰梯形ABCD 中，由//BC AD ，122BC AD ==，60A ∠=︒，E 为AD 中点，所以ABE ∆为等边三角形．如图2,因为O 为BE 的中点，所以1A O BE ⊥．又因为平面1A BE ⊥平面BCDE ，且平面1A BE 平面BCDE BE =，所以1A O ⊥平面BCDE ，所以1A O CE ⊥．………4分（Ⅱ）连结OC ，由已知得CB CE =，又O 为BE 的中点，图2所以OC BE ⊥．由（Ⅰ）知1A O ⊥平面BCDE ，所以11,A O BE A O OC ⊥⊥，所以1,,OA OB OC 两两垂直． 以O 为原点，1,,OB OC OA 分别为,,x y z 轴建立空间直角坐标系（如图）． 因为2BC =，易知13OA OC ==． 所以1(003),(100),(030),(100)A B C E -，，，，，，，，， 所以111(103),(033),(103)A B AC A E =-=-=--，，，，，，． 设平面1A CE 的一个法向量为(,,)x y z =n ，E C D B A 图1 A 1x y z F O BC D EPC B F OD A 1 E由 110,0 AC A E ⎧⋅=⎪⎨⋅=⎪⎩n n 得330, 30.y z x z ⎧-=⎪⎨--=⎪⎩ 即0, 30. y z x z -=⎧⎪⎨+=⎪⎩ 取1z =，得(3,1,1)=-n ．设直线1A B 与平面1A CE 所成角为θ， 则133315sin cos ,5255A B θ--=〈〉===⨯n ． 所以直线1A B 与平面1A CE 所成角的正弦值为155． …………………9分 （Ⅲ）假设在侧棱1A C 上存在点P ，使得//BP 平面1A OF ．设11A P AC λ=，[0,1]λ∈．因为1111BP BA A P BA AC λ=+=+， 所以(103)(033)(1,3,33)BP λλλ=-+-=--，，，，． 易证四边形BCDE 为菱形，且CE BD ⊥，又由（Ⅰ）可知，1A O CE ⊥，所以CE ⊥平面1A OF ． 所以(1,3,0)CE =--为平面1A OF 的一个法向量． 由(1,3,33)(1,3,0)130BP CE λλλ⋅=--⋅--=-=，得1[0,1]3λ=∈． 所以侧棱1A C 上存在点P ，使得//BP 平面1A OF ，且1113A P A C =． …………14分 18．（本小题满分13分）解：（Ⅰ）当3a =时, 21()42ln 2f x x x x =-+-，0x >． 2()4f x x x'=-+-． 则(1)1421f '=-+-=，而17(1)422f =-+=． 所以曲线C 在点(1,(1)f )处的切线方程为712y x -=-，即2250x y -+=． …………………………………………………………………………4分（Ⅱ）依题意当[]1,2x ∈时，曲线C 上的点(),x y 都在不等式组12,,32x x y y x ⎧⎪≤≤⎪≤⎨⎪⎪≤+⎩所表示的平面区域内，等价于当12x ≤≤时，3()2x f x x ≤≤+恒成立． 设()()g x f x x =-211)ln 2x ax a x （=-++-，[]1,2x ∈． 所以21(1)()=+=a x ax a g x x a+x x ---++-'(1)(1))=x x a x---(-． （1）当11a -≤，即2a ≤时，当[]1,2x ∈时，()0g x '≤，()g x 为单调减函数，所以(2)()(1)g g x g ≤≤． 依题意应有131,222221ln20,()()()g a g a a ⎧=-≤⎪⎨⎪=-++-≥⎩ 解得21a a ,.≤⎧⎨≥⎩所以12a ≤≤． （2）若 112a <-<，即23a <<时，当[)1,1x a ∈-，()0g x '≥，()g x 为单调增函 数，当x ∈(]1,2a -，()0g x '<，()g x 为单调减函数．由于3(1)2g >，所以不合题意． （3）当12a -≥，即3a ≥时，注意到15(1)22g a =-≥，显然不合题意． 综上所述，12a ≤≤． …………………………………………13分19．（本小题满分14分）解：（Ⅰ）依题意可知2a =，211c =-=，所以椭圆C 离心率为1222e ==． …………… 3分 （Ⅱ）因为直线l 与x 轴，y 轴分别相交于,A B 两点，所以000,0x y ≠≠． 令0y =，由0012x x y y +=得02x x =，则02(,0)A x ．令0x =，由0012x xy y +=得01y y =，则01(0,)B y ．所以OAB ∆的面积0000112122OAB S OA OB x y x y ∆===．因为点00(,)P x y 在椭圆:C 2212x y +=上，所以22012x y +=． 所以2002001222x y x y =+≥．即0022x y ≤，则0012x y ≥． 所以001122OAB S OA OB x y ∆==≥． 当且仅当22002x y =，即0021,2x y =±=±时，OAB ∆面积的最小值为2．…9分 （Ⅲ）①当00x =时，(0,1)P ±．当直线:1l y =时，易得(1,2)Q -，此时21F P k =-，21F Q k =-．因为22F Q F P k k =，所以三点2,,Q P F 共线．同理，当直线:1l y =-时，三点2,,Q P F 共线．②当00x ≠时，设点(,)Q m n ，因为点Q 与点1F 关于直线l 对称，所以000011,22202() 1.1212x m ny n x m y -⎧⋅+⋅=⎪⎪⎪⎨-⎪⋅-=--⎪+⎪⎩整理得000000240,220.x m y n x y m x n y +--=⎧⎨-+=⎩ 解得220002200000220044,448.4x x y m y x x y y n y x ⎧+-=⎪+⎪⎨+⎪=⎪+⎩ 所以点22000000222200004448(,)44x x y x y y Q y x y x +-+++．又因为200(1,)F P x y =-，220000002222200004448(1,)44x x y x y y F Q y x y x +-+=-++， 且 22200000000000002222220000004448(48)(48)(1)(1)(1)444x x y x y y x y x x y x y y x y x y x +-+--+--⋅-⋅-=⋅+++ 2200000220048(448)4x y x x y y x --+-=⋅+ 222200000002222220000008484(2)84280444y x y x y y y y x y x y x --+-++-⨯+=⋅=⋅=⋅=+++． 所以2//F P 2F Q ．所以点2,,Q P F 三点共线．综上所述，点2,,Q P F 三点共线． …………………………………14分 20．（本小题满分13分）证明：（Ⅰ）当2n =时，{1,2,3,4}S =，令1{1,4}S =，2{2,3}S =,则12S S S =, 且对,(1,2),i x y S i x y ∀∈=>，都有i x y S -∉，所以S 具有性质P ．相应的P 子集为1{1,4}S =，2{2,3}S =． ………… 3分 （Ⅱ）①若31,(1)2n x y T y x -∈≤<≤,由已知x y T -∉, 又31132n n x y --≤-<,所以x y T '-∉．所以'x y T T -∉． ②若,x y T '∈,可设3,3n n x s y r =+=+，,r s T ∈,且3112n r s -≤<≤， 此时31(3)(3)132n n nn x y s r s r --=+-+=-≤-<． 所以'x y T -∉，且x y s r T -=-∉．所以x y TT '-∉．③若y T ∈, 3n x s T '=+∈,s T ∈， 则313331(3)()3(1)3222n n n n nn x y s y s y -+--=+-=-+≥-+=>, 所以x y T -∉．又因为,y T s T ∈∈，所以s y T -∉．所以(3)()3n n x y s y s y T '-=+-=-+∉．所以'x y TT -∉． 综上，对于,'x y T T ∀∈，x y >，都有'x y T T -∉． …………… 8分 （Ⅲ）用数学归纳法证明．（1）由（Ⅰ）可知当2n =时，命题成立，即集合S 具有性质P ．（2）假设n k =(2k ≥)时，命题成立．即1231{1,2,3,,}2k k S S S S -==， 且(1,,)i j S S i j n i j =∅≤≤≠，,(1,2,,),i x y S i k x y ∀∈=>，都有i x y S -∉． 那么 当1n k =+时，记{3|}k i i S s s S '=+∈,， 并构造如下 k +1个集合：111S S S '''=,222S S S '''=,,k k kS S S '''=， 1313131{1,2,,21}222k k k k S +---''=++⨯+， 显然()i j S S i j ''''=∅≠． 又因为131313122k k +--=⨯+，所以112131{1,2,3,,}2k k k S S S S ++-''''''''=． 下面证明 ¢¢S i 中任意两个元素之差不等于 ¢¢S i 中的任一元素(1,2,,1)i k =+．①若两个元素13131,22k k k r s S +--''++∈,31112k r s -≤<≤+, 则313131()()222k k k s r s r ---+-+=-≤, 所以13131()()22k k k s r S +--''+-+∉． ②若两个元素都属于i i i S S S '''=(1)i k ≤≤,由（Ⅱ）可知，i S ''中任意两个元素之差不等于i S ''中的任一数(1,2,,1)i k =+． 从而，1n k =+时命题成立．综上所述，对任意正整数2n ≥，集合S 具有性质P ．………………………13分。

2016年北京市朝阳区高三理科上学期人教A版数学期末考试试卷一、选择题（共8小题；共40分）1. 已知全集，集合，，则A. B.C. D.2. 在复平面内，复数对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 下列函数中，既是偶函数，又在区间上单调递增的是A. B. C. D.4. 若，且，则“函数在上是减函数”是“函数在上是增函数”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件5. 从，，，，中任选两个不同的数字组成一个两位数，其中偶数的个数是A. B. C. D.6. 某四棱锥的三视图如图所示，其俯视图为等腰直角三角形，则该四棱锥的体积为A. B. C. D.7. 在中，，点是边上的动点，且，，，则当取得最大值时，的值为A. B. C. D.8. 某校高三（1）班名学生参加跳远和掷实心球两项测试．跳远和掷实心球两项测试成绩合格的人数分别为人和人，这两项成绩均不合格的有人，则这两项成绩均合格的人数是A. B. C. D.二、填空题（共6小题；共30分）9. 已知双曲线的一条渐近线方程为，则等于______．10. 已知等差数列的前项和为．若，，则 ______， ______．11. 执行如图所示的程序框图，则输出的结果为______．12. 在中，已知，，则 ______．13. 设为不等式组表示的平面区域，对于区域内除原点外的任一点，则的最大值是______，的取值范围是______．14. 若集合满足：，都有，，则称集合是封闭的．显然，整数集、有理数集都是封闭的．对于封闭的集合，是从集合到集合的一个函数，①如果都有，就称是保加法的；②如果都有，就称是保乘法的；③如果既是保加法的，又是保乘法的，就称在上是保运算的．在上述定义下，集合 ______ 封闭的（填“是”或“否”）；若函数在上保运算，并且是不恒为零的函数，请写出满足条件的一个函数 ______．三、解答题（共6小题；共78分）15. 已知函数．（1）求的最小正周期；（2）求在区间上的最大值和最小值．16. 甲、乙两位同学参加数学文化知识竞赛培训．现分别从他们在培训期间参加的若干次测试成绩中随机抽取次，记录如下：甲：乙：（1）用茎叶图表示这两组数据；（2）现要从中选派一人参加正式比赛，从所抽取的两组数据分析，你认为选派哪位同学参加较为合适?并说明理由；（3）若对甲同学在今后的次测试成绩进行预测，记这次成绩中高于分的次数为（将甲次成绩中高于分的频率视为概率），求的分布列及数学期望．17. 在如图所示的几何体中，四边形为正方形，四边形为直角梯形，且，，平面平面，．（1）求证： 平面；（2）若二面角为直二面角，（i）求直线与平面所成角的大小；（ii）棱上是否存在点，使得平面?若存在，求出的值；若不存在，请说明理由．18. 已知椭圆：上的动点与其顶点，不重合．（1）求证：直线与的斜率乘积为定值；（2）设点，在椭圆上，为坐标原点，当，时，求的面积．19. 已知函数，，其中，为自然对数的底数．（1）若函数的图象在点处的切线过坐标原点，求实数的值；（2）若在上为单调递增函数，求实数的取值范围；（3）当时，对于满足的两个实数，若存在，使得成立，试比较与的大小．20. 设，是正整数，数列：，，，，其中是集合中互不相同的元素．若数列满足：只要存在，使，总存在有，则称数列是“好数列”．（1）当，时，（ⅰ）若数列：，，，，，是一个“好数列”，试写出，的值，并判断数列：，，，，，是否是一个“好数列”?（ⅱ）若数列：，，，，，是“好数列”，且，求，，，共有多少种不同的取值?（2）若数列是“好数列”，且是偶数，证明：．答案第一部分1. B2. D3. D4. A5. C6. B7. C8. B第二部分9.10. ；11.12.13. ；14. 是；第三部分15. （1）．所以．（2）因为，所以．所以．当时，函数取到最小值，当时，函数取到最大值．16. （1）作出茎叶图如下：（2）派甲参赛比较合适．理由如下：甲乙甲乙因为甲乙，甲乙，所以，甲的成绩较稳定，派甲参赛比较合适．注：本小题的结论及理由均不唯一，如果考生能从统计学的角度分析，给出其他合理回答，同样给分．如派乙参赛比较合适．理由如下：从统计的角度看，甲获得分以上（含分）的频率为，乙获得分以上（含分）的频率为．因为，所以派乙参赛比较合适．（3）记“甲同学在一次数学竞赛中成绩高于分”为事件，．随机变量的可能取值为，，，，且．所以，．所以变量的分布列为：．（或．）17. （1）连接，设，为正方形，所以为中点．设为的中点，连接，，则，且．由已知，且，所以，．所以四边形为平行四边形．所以，即．因为平面，平面，所以 平面．（2）（i）由已知，，，所以．因为二面角为直二面角，所以平面平面．所以平面，所以，．四边形为正方形，所以．所以，，两两垂直．以为原点，，，分别为，，轴建立空间直角坐标系（如图）．，所以，，，，，，所以，，．设平面的一个法向量为，由得即取，得．设直线与平面所成角为，则，因为，所以．即直线与平面所成角的大小为．（ii）假设棱上存在点，使得平面．设，则．设，则，因为，所以．所以，，，所以点坐标为．因为，所以．又，，所以解得．因为，所以上存在点，使得平面，且．（另解）假设棱上存在点，使得平面．设，则．设，则，因为，所以．所以，，，所以点坐标为．因为，所以．设平面的一个法向量为，则由，，得取，得．由，即，可得解得．因为，所以上存在点，使得平面，且．18. （1）设，则．所以直线与．（2）依题直线，的斜率乘积为．①当直线的斜率不存在时，直线，的斜率为，设直线的方程是，由得，．取，则．所以的面积为．②当直线的斜率存在时，设直线的方程是，由得．因为，在椭圆上，所以，解得．设，，则，．设点到直线的距离为，则．所以的面积为因为，，直线，的斜率乘积为，所以．所以由，得由，得综上所述，．19. （1）因为，所以．则，．所以函数的图象在点处的切线为：．因为切线过坐标原点，所以，即．所以．（2），要使在上为单调递增函数，只要，令，①当时，，在内，所以，函数在上为单调递增函数．②当时，是开口向上的二次函数，其对称轴为，所以在上递增，为使在上单调递增，必须，而此时，产生矛盾．所以此种情况不符合题意．③当时，是开口向下的二次函数，为使在上单调递增，必须，即在上恒成立，所以又，所以．综合①②③得实数的取值范围为．（3），．因为对满足的实数，存在，使得成立，所以，即，从而<br>\（\[\begin{split}\ln {x_0} - \ln {x_1}& = \dfrac{{{x_1}\ln {x_1} - {x_2}\ln {x_2}}}{{{x_1} -{x_2}}} - 1 - \ln {x_1}\\& = \dfrac{{{x_2}\ln {x_1} - {x_2}\ln {x_2} + {x_2} - {x_1}}}{{{x_1} -{x_2}}}\\&= \dfrac{{\ln \dfrac{x_1}{x_2} + 1 - \dfrac{x_1}{x_2}}}{{\dfrac{x_1}{x_2} - 1}}.\end{split}\]\）<br>设，其中，则，则，因而在区间上单调递增，，因为，所以，从而，又．所以，即．20. （1）（ⅰ）因为，，数列：，，，，，是一个“好数列”，所以，，或，，数列：，，，，，也是一个“好数列”．（ⅱ）由（ⅰ）可知，数列必含，两项，若剩下两项从，，，中任取，则都符合条件，有种；若剩下两项从，，，中任取一个，则另一项必对应，，，中的一个，有种；若取，则，，“好数列”必超过项，不符合；若取，则，另一项可从，，，中任取一个，有种；若取，则，，“好数列”必超过项，不符合；若取，则，符合条件，若取，则易知“好数列”必超过项，不符合；综上，，，，共有种不同的取值．（2）由（Ⅰ）易知，一个“好数列”各项任意排列后，还是一个“好数列”．又“好数列”，，，各项互不相同，所以，不妨设．把数列配对：，，，，只要证明每一对和数都不小于即可．用反证法，假设存在，使，因为数列单调递增，所以，又因为“好数列”，故存在，使得，显然，故，所以只有个不同取值，而有个不同取值，矛盾．所以，，，，每一对和数都不小于，故，即．。

2016-2017学年北京市朝阳区高三（上）期末数学试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．（5分）已知全集U=R，集合A={x|2x＜1}，B={x|x﹣2＜0}，则（∁U A）∩B=（）A．{x|x＞2}B．{x|0≤x＜2}C．{x|0＜x≤2}D．{x|x≤2}2．（5分）在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）下列函数中，既是偶函数，又在区间[0，1]上单调递增的是（）A．y=cosx B．y=﹣x2C．D．y=|sinx|4．（5分）若a＞0，且a≠1，则“函数y=a x在R上是减函数”是“函数y=（2﹣a）x3在R上是增函数”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件5．（5分）从0，1，2，3，4中任选两个不同的数字组成一个两位数，其中偶数的个数是（）A．6 B．8 C．10 D．126．（5分）某四棱锥的三视图如图所示，其俯视图为等腰直角三角形，则该四棱锥的体积为（）A．B．C．D．47．（5分）在Rt△ABC中，∠A=90°，点D是边BC上的动点，且||=3，||=4，=λ+μ（λ＞0，μ＞0），则当λμ取得最大值时，||的值为（）A．B．3 C．D．8．（5分）某校高三（1）班32名学生参加跳远和掷实心球两项测试．跳远和掷实心球两项测试成绩合格的人数分别为26人和23人，这两项成绩均不合格的有3人，则这两项成绩均合格的人数是（）A．23 B．20 C．21 D．19二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．（5分）已知双曲线的一条渐近线方程为3x+2y=0，则b等于．10．（5分）已知等差数列{a n}的前n项和为S n．若a1=2，S2=a3，则a2=，S10=．11．（5分）执行如图所示的程序框图，则输出的结果是．12．（5分）在△ABC中，已知，则∠C=．13．（5分）设D为不等式组表示的平面区域，对于区域D内除原点外的任一点A（x，y），则2x+y的最大值是，的取值范围是．14．（5分）若集合M满足：∀x，y∈M，都有x+y∈M，xy∈M，则称集合M是封闭的．显然，整数集Z，有理数集Q都是封闭的．对于封闭的集合M（M⊆R），f：M→M是从集合到集合的一个函数，①如果都有f（x+y）=f（x）+f（y），就称是保加法的；②如果∀x，y∈M都有f（xy）=f（x）•f（y），就称f是保乘法的；③如果f既是保加法的，又是保乘法的，就称f在M上是保运算的．在上述定义下，集合封闭的（填“是”或“否”）；若函数f（x）在Q上保运算，并且是不恒为零的函数，请写出满足条件的一个函数f（x）=．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数f（x）=2sinxcosx+2cos2x﹣1（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间[﹣，]上的最大值和最小值．16．（13分）甲、乙两位同学参加数学文化知识竞赛培训．现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下：甲：8281797895889384乙：9295807583809085（Ⅰ）用茎叶图表示这两组数据；（Ⅱ）现要从中选派一人参加正式比赛，从所抽取的两组数据分析，你认为选派哪位同学参加较为合适？并说明理由；（Ⅲ）若对甲同学在今后的3次测试成绩进行预测，记这3次成绩中高于80分的次数为ξ（将甲8次成绩中高于80分的频率视为概率），求ξ的分布列及数学期望Eξ．17．（14分）在如图所示的几何体中，四边形ABCD为正方形，四边形ABEF为直角梯形，且AF∥BE，AB⊥BE，平面ABCD∩平面ABEF=AB，AB=BE=2AF=2．（Ⅰ）求证：AC∥平面DEF；（Ⅱ）若二面角D﹣AB﹣E为直二面角，（i）求直线AC与平面CDE所成角的大小；（ii）棱DE上是否存在点P，使得BP⊥平面DEF？若存在，求出的值；若不存在，请说明理由．18．（13分）已知椭圆上的动点P与其顶点，不重合．（Ⅰ）求证：直线PA与PB的斜率乘积为定值；（Ⅱ）设点M，N在椭圆C上，O为坐标原点，当OM∥PA，ON∥PB时，求△OMN的面积．19．（14分）设函数f（x）=ln（x﹣1）+ax2+x+1，g（x）=（x﹣1）e x+ax2，a∈R．（Ⅰ）当a=1时，求函数f（x）在点（2，f（2））处的切线方程；（Ⅱ）若函数g（x）有两个零点，试求a的取值范围；（Ⅲ）证明f（x）≤g（x）20．（13分）设m，n（3≤m≤n）是正整数，数列A m：a1，a2，…，a m，其中a i （1≤i≤m）是集合{1，2，3，…，n}中互不相同的元素．若数列A m满足：只要存在i，j（1≤i＜j≤m）使a i+a j≤n，总存在k（1≤k≤m）有a i+a j=a k，则称数列A m是“好数列”．（Ⅰ）当m=6，n=100时，（ⅰ）若数列A6：11，78，x，y，97，90是一个“好数列”，试写出x，y的值，并判断数列：11，78，90，x，97，y是否是一个“好数列”？（ⅱ）若数列A6：11，78，a，b，c，d是“好数列”，且a＜b＜c＜d，求a，b，c，d共有多少种不同的取值？（Ⅱ）若数列A m是“好数列”，且m是偶数，证明：．2016-2017学年北京市朝阳区高三（上）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．（5分）已知全集U=R，集合A={x|2x＜1}，B={x|x﹣2＜0}，则（∁U A）∩B=（）A．{x|x＞2}B．{x|0≤x＜2}C．{x|0＜x≤2}D．{x|x≤2}【解答】解：A={x|2x＜1}={x|x＜0}，B={x|x﹣2＜0}={x|x＜2}，∁U A={x|x≥0}，则（∁U A）∩B={x|0≤x＜2}，故选：B．2．（5分）在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：在复平面内，复数==1﹣i对应的点（1，﹣1）位于第四象限．故选：D．3．（5分）下列函数中，既是偶函数，又在区间[0，1]上单调递增的是（）A．y=cosx B．y=﹣x2C．D．y=|sinx|【解答】解：A．y=cosx是偶函数，在区间[0，1]上单调递减，不满足条件．B．y=﹣x2是偶函数，在区间[0，1]上单调递减，不满足条件．C.是偶函数，当x≥0时=（）x在区间[0，1]上单调递减，不满足条件．D．y=|sinx|是偶函数，在区间[0，1]上单调递增，满足条件．故选：D．4．（5分）若a＞0，且a≠1，则“函数y=a x在R上是减函数”是“函数y=（2﹣a）x3在R上是增函数”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：若函数y=a x在R上是减函数，则0＜a＜1，此时2﹣a＞0，则函数y=（2﹣a）x3在R上是增函数成立，即充分性成立，若函数y=（2﹣a）x3在R上是增函数，则2﹣a＞0，即0＜a＜2，则函数y=a x在R上不一定是减函数，即必要性不成立，即“函数y=a x在R上是减函数”是“函数y=（2﹣a）x3在R上是增函数”的充分不必要条件，故选：A．5．（5分）从0，1，2，3，4中任选两个不同的数字组成一个两位数，其中偶数的个数是（）A．6 B．8 C．10 D．12【解答】解：由题意，末尾是0，2，4末尾是0时，有4个；末尾是2时，有3个；末尾是4时，有3个，所以共有4+3+3=10个故选：C．6．（5分）某四棱锥的三视图如图所示，其俯视图为等腰直角三角形，则该四棱锥的体积为（）A．B．C．D．4【解答】解：由三视图知：几何体为四棱锥，且四棱锥的高为，底面是边长为2，矩形，∴几何体的体积V==．故选：B．7．（5分）在Rt△ABC中，∠A=90°，点D是边BC上的动点，且||=3，||=4，=λ+μ（λ＞0，μ＞0），则当λμ取得最大值时，||的值为（）A．B．3 C．D．【解答】解：将三角形放入坐标系中，则C（0，4），B（3，0），∵=λ+μ（λ＞0，μ＞0），∴λ+μ=1，则1=λ+μ≥2，即λμ≤，当且仅当λ=μ=时取等号，此时=λ+μ=+=（3，0）+（0，4）=（，2）则||==，故选：C．8．（5分）某校高三（1）班32名学生参加跳远和掷实心球两项测试．跳远和掷实心球两项测试成绩合格的人数分别为26人和23人，这两项成绩均不合格的有3人，则这两项成绩均合格的人数是（）A．23 B．20 C．21 D．19【解答】解：设这两项成绩均合格的人数为x，则跳远合格掷实心球不合格的人数为26﹣x，则26﹣x+23+3=32，得x=20，即这两项成绩均合格的人数是20人，故选：B．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．（5分）已知双曲线的一条渐近线方程为3x+2y=0，则b等于3．【解答】解：双曲线的一条渐近线方程为3x+2y=0，∴=，解得b=3，故答案为：310．（5分）已知等差数列{a n}的前n项和为S n．若a1=2，S2=a3，则a2=4，S10=110．【解答】解：设等差数列{a n}的公差为d，∵a1=2，S2=a3，∴2a1+d=a1+2d，即2=d，∴a2=2+2=4．S10=10××2=110．故答案为：4，110．11．（5分）执行如图所示的程序框图，则输出的结果是20．【解答】解：执行程序框图，有a=1，b=1，s=2c=2，s=4不满足条件c＞5，a=1，b=2，c=3，s=7不满足条件c＞5，a=2，b=3，c=5，s=12不满足条件c＞5，a=3，b=5，c=8，s=20满足条件c＞5，退出循环，输出s的值为20．故答案为：20．12．（5分）在△ABC中，已知，则∠C=105°．【解答】解：由题意：已知，即b=a由正弦定理=，则有sinA=，∵0°＜A＜135°∴A=30°则C=180°﹣30°﹣45°=105°故答案为：105°13．（5分）设D为不等式组表示的平面区域，对于区域D内除原点外的任一点A（x，y），则2x+y的最大值是，的取值范围是[﹣，0] ．【解答】解：先根据约束条件不等式组画出可行域：当直线2x+y=t过点A时，2x+y取得最大值，由，可得A（，）时，z最大是2×=，由约束条件x﹣y≤0，可知≤0，令z=，可得z2==1﹣，令t=，由可行域可得∈（﹣∞，﹣1]∪[1，+∞）．求解的最小值，就是解z2的最大值，即1﹣的最大值，可知∈（﹣∞，﹣1]，显然=﹣1时，z2取得最大值2．所以z，的取值范围是[﹣，0]．故答案为：．[﹣，0]．14．（5分）若集合M满足：∀x，y∈M，都有x+y∈M，xy∈M，则称集合M是封闭的．显然，整数集Z，有理数集Q都是封闭的．对于封闭的集合M（M⊆R），f：M→M是从集合到集合的一个函数，①如果都有f（x+y）=f（x）+f（y），就称是保加法的；②如果∀x，y∈M都有f（xy）=f（x）•f（y），就称f是保乘法的；③如果f既是保加法的，又是保乘法的，就称f在M上是保运算的．在上述定义下，集合是封闭的（填“是”或“否”）；若函数f （x）在Q上保运算，并且是不恒为零的函数，请写出满足条件的一个函数f（x）=f（x）=x，x∈Q．【解答】解：设x=m+n，y=a+b，m，n，a，b∈Q，∴x+y=m+n+a+b=（m+a）+（n+b），m+a，n+b∈Q，即f（x+y）=f（x）+f（y），∴xy=（m+n）（a+b）=3ma+（mb+an）+bn=（mb+an）+（bn+3ma），mb，an，bn，3ma∈Q，∴f（xy）=f（x）•f（y），∴上述定义下，集合是封闭的，当f（x）=x，x∈Q满足条件，设m，n∈Q，∴f（m+n）=m+n=f（m）+f（n），f（mn）=mn=f（m）•f（n），故答案为：是，f（x）=x，x∈Q三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数f（x）=2sinxcosx+2cos2x﹣1（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间[﹣，]上的最大值和最小值．【解答】解：（Ⅰ）∵f（x）=2sinxcosx+2cos2x﹣1=sin2x+cos2x=2sin（2x+）∴T=．（Ⅱ）∵x∈[﹣，]，∴2x+∈[﹣，]∴﹣1≤2sin（2x+）≤2∴函数f（x）在区间[﹣，]上的最小值为﹣1，最大值为2．16．（13分）甲、乙两位同学参加数学文化知识竞赛培训．现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下：甲：8281797895889384乙：9295807583809085（Ⅰ）用茎叶图表示这两组数据；（Ⅱ）现要从中选派一人参加正式比赛，从所抽取的两组数据分析，你认为选派哪位同学参加较为合适？并说明理由；（Ⅲ）若对甲同学在今后的3次测试成绩进行预测，记这3次成绩中高于80分的次数为ξ（将甲8次成绩中高于80分的频率视为概率），求ξ的分布列及数学期望Eξ．【解答】解：（Ⅰ）作出茎叶图如下：（Ⅱ）派甲参赛比较合适．理由如下：，，（88﹣85）2+（93﹣85）2+（95﹣85）2]=35.5，（90﹣85）2+（92﹣85）2+（95﹣85）2]=41．因为=，，所以，甲的成绩较稳定，派甲参赛比较合适．注：本小题的结论及理由均不唯一，如果考生能从统计学的角度分析，给出其他合理回答，同样给分．如派乙参赛比较合适．理由如下：从统计的角度看，甲获得8（5分）以上（含85分）的频率为，乙获得8（5分）以上（含85分）的频率为．因为f2＞f1，所以派乙参赛比较合适．（Ⅲ）记“甲同学在一次数学竞赛中成绩高于8（0分）”为事件A，．随机变量ξ的可能取值为0，1，2，3，且．∴，k=0，1，2，3．所以变量ξ的分布列为：ξ0123P．（或．）17．（14分）在如图所示的几何体中，四边形ABCD为正方形，四边形ABEF为直角梯形，且AF∥BE，AB⊥BE，平面ABCD∩平面ABEF=AB，AB=BE=2AF=2．（Ⅰ）求证：AC∥平面DEF；（Ⅱ）若二面角D﹣AB﹣E为直二面角，（i）求直线AC与平面CDE所成角的大小；（ii）棱DE上是否存在点P，使得BP⊥平面DEF？若存在，求出的值；若不存在，请说明理由．【解答】（本小题满分14分）证明：（Ⅰ）连结BD，设AC∩BD=O，因为四边形ABCD为正方形，所以O为BD中点．设G为DE的中点，连结OG，FG，则OG∥BE，且．由已知AF∥BE，且，所以AF∥OG，OG=AF．所以四边形AOGF为平行四边形．所以AO∥FG，即AC∥FG．因为AC⊄平面DEF，FG⊂平面DEF，所以AC∥平面DEF．…（5分）解：（Ⅱ）（i）由已知，AF∥BE，AB⊥BE，所以AF⊥AB．因为二面角D﹣AB﹣E为直二面角，所以平面ABCD⊥平面ABEF．所以AF⊥平面ABCD，所以AF⊥AD，AF⊥AB．四边形ABCD为正方形，所以AB⊥AD．所以AD，AB，AF两两垂直．以A为原点，AD，AB，AF分别为x，y，z轴建立空间直角坐标系（如图）．因为AB=BE=2AF=2，所以A（0，0，0），B（0，2，0），C（2，2，0），D（2，0，0），E（0，2，2），F（0，0，1），所以．设平面CDE的一个法向量为n=（x，y，z），由得即取x=1，得n=（1，0，1）．设直线AC与平面CDE所成角为θ，则，因为0≤θ≤90°，所以θ=30°．即直线AC与平面CDE所成角的大小为30°．…（9分）（ii）假设棱DE上存在点P，使得BP⊥平面DEF．设，则．设P（x，y，z），则，因为，所以（x﹣2，y，z）=λ（﹣2，2，2）．所以x﹣2=﹣2λ，y=2λ，z=2λ，所以P点坐标为（2﹣2λ，2λ，2λ）．因为B（0，2，0），所以．又，所以，解得．因为，所以DE上存在点P，使得BP⊥平面DEF，且．（另解）假设棱DE上存在点P，使得BP⊥平面DEF．设，则．设P（x，y，z），则，因为，所以（x﹣2，y，z）=λ（﹣2，2，2）．所以x﹣2=﹣2λ，y=2λ，z=2λ，所以P点坐标为（2﹣2λ，2λ，2λ）．因为B（0，2，0），所以．设平面DEF的一个法向量为=（x0，y0，z0），则，由，得取x0=1，得=（1，﹣1，2）．由，即（2﹣2λ，2λ﹣2，2λ）=μ（1，﹣1，2），可得解得．因为，所以DE上存在点P，使得BP⊥平面DEF，且．…（14分）18．（13分）已知椭圆上的动点P与其顶点，不重合．（Ⅰ）求证：直线PA与PB的斜率乘积为定值；（Ⅱ）设点M，N在椭圆C上，O为坐标原点，当OM∥PA，ON∥PB时，求△OMN的面积．【解答】（本小题满分13分）解：（Ⅰ）证明：设P（x0，y0），则．所以直线PA与PB的斜率乘积为．…（4分）（Ⅱ）依题直线OM，ON的斜率乘积为．①当直线MN的斜率不存在时，直线OM，ON的斜率为，设直线OM的方程是，由得，y=±1．取，则．所以△OMN的面积为．②当直线MN的斜率存在时，设直线MN的方程是y=kx+m，由得（3k2+2）x2+6kmx+3m2﹣6=0．因为M，N在椭圆C上，所以△=36k2m2﹣4（3k2+2）（3m2﹣6）＞0，解得3k2﹣m2+2＞0．设M（x1，y1），N（x2，y2），则，．=．设点O到直线MN的距离为d，则．所以△OMN的面积为…①．因为OM∥PA，ON∥PB，直线OM，ON的斜率乘积为，所以．所以=．由，得3k2+2=2m2…②由①②，得．综上所述，．…（13分）19．（14分）设函数f（x）=ln（x﹣1）+ax2+x+1，g（x）=（x﹣1）e x+ax2，a∈R．（Ⅰ）当a=1时，求函数f（x）在点（2，f（2））处的切线方程；（Ⅱ）若函数g（x）有两个零点，试求a的取值范围；（Ⅲ）证明f（x）≤g（x）【解答】解：（Ⅰ）函数f（x）的定义域是（1，+∞），．当a=1时，f'（2）=4a+2=6，f（2）=4a+3=7．所以函数f（x）在点（2，f（2））处的切线方程为y﹣7=6（x﹣2）．即y=6x﹣5．…（4分）（Ⅱ）函数g（x）的定义域为R，由已知得g'（x）=x（e x+2a）．①当a=0时，函数g（x）=（x﹣1）e x只有一个零点；②当a＞0，因为e x+2a＞0，当x∈（﹣∞，0）时，g'（x）＜0；当x∈（0，+∞）时，g'（x）＞0．所以函数g（x）在（﹣∞，0）上单调递减，在（0，+∞）上单调递增．又g（0）=﹣1，g（1）=a，因为x＜0，所以x﹣1＜0，e x＜1，所以e x（x﹣1）＞x﹣1，所以g（x）＞ax2+x ﹣1取，显然x 0＜0且g （x 0）＞0所以g （0）g （1）＜0，g （x 0）g （0）＜0．由零点存在性定理及函数的单调性知，函数有两个零点．③当a ＜0时，由g'（x ）=x （e x +2a ）=0，得x=0，或x=ln （﹣2a ）． ⅰ） 当，则ln （﹣2a ）＞0．当x 变化时，g'（x ），g （x ）变化情况如下表：x（﹣∞，0）（0，ln （﹣2a ））ln （﹣2a ） （ln （﹣2a ），+∞） g'（x ） + 0 ﹣ 0+ g （x ）↗﹣1↘↗注意到g （0）=﹣1，所以函数g （x ）至多有一个零点，不符合题意． ⅱ） 当，则ln （﹣2a ）=0，g （x ）在（﹣∞，+∞）单调递增，函数g （x ）至多有一个零点，不符合题意． 若，则ln （﹣2a ）≤0．当x 变化时，g'（x ），g （x ）变化情况如下表：x（﹣∞，ln （﹣2a ））ln （﹣2a ） （ln （﹣2a ），0） 0 （0，+∞）g'（x ） + 0﹣ 0 + g （x ）↗↘﹣1↗注意到当x ＜0，a ＜0时，g （x ）=（x ﹣1）e x +ax 2＜0，g （0）=﹣1，所以函数g （x ）至多有一个零点，不符合题意． 综上，a 的取值范围是（0，+∞）．…（9分）（Ⅲ）证明：g （x ）﹣f （x ）=（x ﹣1）e x ﹣ln （x ﹣1）﹣x ﹣1．设h （x ）=（x ﹣1）e x ﹣ln （x ﹣1）﹣x ﹣1，其定义域为（1，+∞），则证明h （x ）≥0即可． 因为，取，则，且h'（2）＞0．又因为，所以函数h'（x）在（1，+∞）上单增．所以h'（x）=0有唯一的实根x0∈（1，2），且．当1＜x＜x0时，h'（x）＜0；当x＞x0时，h'（x）＞0．所以函数h（x）的最小值为h（x0）．所以=1+x0﹣x0﹣1=0．所以f（x）≤g（x）．…（14分）20．（13分）设m，n（3≤m≤n）是正整数，数列A m：a1，a2，…，a m，其中a i （1≤i≤m）是集合{1，2，3，…，n}中互不相同的元素．若数列A m满足：只要存在i，j（1≤i＜j≤m）使a i+a j≤n，总存在k（1≤k≤m）有a i+a j=a k，则称数列A m是“好数列”．（Ⅰ）当m=6，n=100时，（ⅰ）若数列A6：11，78，x，y，97，90是一个“好数列”，试写出x，y的值，并判断数列：11，78，90，x，97，y是否是一个“好数列”？（ⅱ）若数列A6：11，78，a，b，c，d是“好数列”，且a＜b＜c＜d，求a，b，c，d共有多少种不同的取值？（Ⅱ）若数列A m是“好数列”，且m是偶数，证明：．【解答】（本小题13分）解：（Ⅰ）（ⅰ）∵m=6，n=100，数列A6：11，78，x，y，97，90是一个“好数列”，∴x=89，y=100，或x=100，y=89，数列：11，78，90，x，97，y也是一个“好数列”．…（3分）（ⅱ）由（ⅰ）可知，数列必含89，100两项，若剩下两项从90，91，…，99中任取，则都符合条件，有种；若剩下两项从79，80，…，88中任取一个，则另一项必对应90，91，…，99中的一个，有10种；若取68≤a≤77，则79≤11+a≤88，90≤22+a≤99，“好数列”必超过6项，不符合；若取a=67，则11+a=78∈A6，另一项可从90，91，…，99中任取一个，有10种；若取56＜a＜67，则67＜11+a＜78，78＜22+a＜89，“好数列”必超过6项，不符合；若取a=56，则b=67，符合条件，若取a ＜56，则易知“好数列”必超过6项，不符合； 综上，a ，b ，c ，d 共有66种不同的取值． …（7分）证明：（Ⅱ）由（Ⅰ）易知，一个“好数列”各项任意排列后，还是一个“好数列”． 又“好数列”a 1，a 2，…，a m 各项互不相同，所以，不妨设a 1＜a 2＜…＜a m ． 把数列配对：，只要证明每一对和数都不小于n +1即可． 用反证法，假设存在，使a j +a m +1﹣j ≤n ，因为数列单调递增，所以a m ﹣j +1＜a 1+a m ﹣j +1＜a 2+a m ﹣j +1＜…＜a j +a m ﹣j +1≤n ， 又因为“好数列”，故存在1≤k ≤m ，使得a i +a m +1﹣j =a k （1≤i ≤j ），显然a k ＞a m +1﹣j ，故k ＞m +1﹣j ，所以a k 只有j ﹣1个不同取值，而a i +a m +1﹣j 有j 个不同取值，矛盾． 所以，每一对和数都不小于n +1，故，即．…（13分）赠送—高中数学知识点【2.1.1】指数与指数幂的运算 （1）根式的概念①如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n n a n 是偶数时，正数a 的正的n n a 表示，负的n 次方根用符号n a -0的n 次方根是0；负数a 没有n 次方根．n a n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：()n n a a =；当n 为奇数时，nn a a =；当n 为偶数时，(0)|| (0)nn a a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,m n m na a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：11()()0,,,m m m nn n aa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义． 注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质 函数名称指数函数定义函数(0xy a a =>且1)a ≠叫做指数函数图象1a >01a <<定义域Rxa y =xy(0,1)O1y =xa y =xy (0,1)O 1y =值域 (0,)+∞过定点 图象过定点(0,1)，即当0x =时，1y =．奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数函数值的 变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对 图象的影响 在第一象限内，a 越大图象越高；在第二象限内，a 越大图象越低．〖2.2〗对数函数【2.2.1】对数与对数运算（1）对数的定义①若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =⇔=>≠>． （2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）． （4）对数的运算性质 如果0,1,0,0a a M N >≠>>，那么①加法：log log log ()a a a M N MN += ②减法：log log log a a a MM N N-= ③数乘：log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质（5）对数函数函数 名称对数函数定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a >01a <<定义域 (0,)+∞ 值域 R过定点 图象过定点(1,0)，即当1x =时，0y =．奇偶性 非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的 变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对 图象的影响在第一象限内，a 越大图象越靠低；在第四象限内，a 越大图象越靠高．x yO(1,0)1x =log a y x=xyO (1,0)1x =log a y x=。

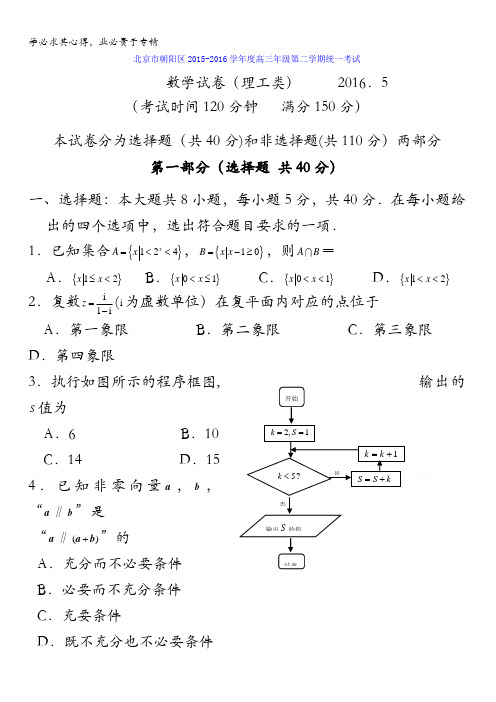
开始输出S 的值2,1k S ==5?k <1k k =+ S S k=+结束是否 北京市朝阳区2015-2016学年度高三年级第二学期统一考试数学试卷（理工类） 2016．5（考试时间120分钟 满分150分）本试卷分为选择题（共40分)和非选择题(共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项． 1．已知集合{}124xA x =<<，{}10B x x =-≥，则A B ＝A ．{}12x x ≤<B ．{}01x x <≤C ．{}01x x <<D ．{}12x x <<2．复数i1iz =-(i 为虚数单位）在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3．执行如图所示的程序框图,输出的S值为A ．6B ．10C ．14D ．15 4．已知非零向量a ，b ，“a ∥b ”是 “a ∥()+a b ”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5．同时具有性质:“①最小正周期是π; ②图象关于直线3x π=对称;③在区间5,6π⎡⎤π⎢⎥⎣⎦上是单调递增函数”的一个函数可以是A ．cos()26x y π=+ B ．sin(2)6y x 5π=+C ．cos(2)3y x π=-D ．sin(2)6y x π=-6．已知函数1,2,()2log ,2a x x f x x x -≤⎧=⎨+>⎩(0a >且1)a ≠的最大值为1,则a 的取值范围是A ．112[,) B ．01(,) C ．102(,] D ．1(,)+∞7．某学校高三年级有两个文科班,四个理科班，现每个班指定1人,对各班的卫生进行检 查．若每班只安排一人检查,且文科班学生不检查文科班，理科班学生不检查自己所在的班，则不同安排方法的种数是A ．48B ．72C ．84D ．1688．已知正方体1111A B C D A B C D-的棱长为2，E 是棱11D C 的中点，点F 在正方体内部或正方体的表面上，且EF ∥平面11A BC ，则动点F 的轨迹所形成的区域面积是A ．92BCD第二部分(非选择题 共110分）二、填空题:本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．双曲线22:13x C y -=的渐近线方程是 ；若抛物线22(0)ypx p =>的焦点与双曲线C 的一个焦点重合，则p = ． 10．如图,P 为⊙O 外一点,PA 是⊙O 的切线，A为切点，割线PBC与⊙O 相交于,B C 两点,且3PC PA =，D 为线段BC 的中点，AD 的延长线交⊙O 于点E ．若1PB =，则PA 的长为______； AD DE ⋅的值是．11．已知等边ABC ∆的边长为3，D 是BC 边上一点，若1BD =，则AC AD ⋅的值是______．12．已知关于,x y 的不等式组0,,2,2x y x x y x y k≥⎧⎪≥⎪⎨+≤⎪⎪-≥⎩所表示的平面区域D 为三角形区域,则实数k 的取值范围是 ．13．为了响应政府推进“菜篮子"工程建设的号召,某经销商投资60万元建了一个蔬菜生产基地.第一年支出各种费用8万元，以后每年支出的费用比上一年多2万元。

开始输出S 的值2,1k S ==5?k <1k k =+S S k =+结束 是否 北京市朝阳区2015-2016学年度高三年级第二学期统一考试数学试卷（理工类） 2016．5（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．已知集合{}124xA x =<<，{}10B x x =-≥，则A B I ＝A ．{}12x x ≤<B ．{}01x x <≤C ．{}01x x <<D ．{}12x x << 2．复数i1iz =-（i 为虚数单位）在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3．执行如图所示的程序框图，输出的S 值为 A ．6 B ．10 C ．14 D ．15 4．已知非零向量a ，b ，“a ∥b ”是 “a ∥()+a b ”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5．同时具有性质:“①最小正周期是π； ②图象关于直线3x π=对称； ③在区间5,6π⎡⎤π⎢⎥⎣⎦上是单调递增函数”的一个函数可以是 A ．cos()26x y π=+ B ．sin(2)6y x 5π=+C ．cos(2)3y x π=-D ．sin(2)6y x π=-6．已知函数1,2,()2log ,2a x x f x x x -≤⎧=⎨+>⎩(0a >且1)a ≠的最大值为1,则a 的取值范围是A ．112[,) B ．01(,) C ．102(,] D ．1(,)+∞7．某学校高三年级有两个文科班，四个理科班，现每个班指定1人，对各班的卫生进行检 查．若每班只安排一人检查，且文科班学生不检查文科班，理科班学生不检查自己所在的班，则不同安排方法的种数是A ．48B ．72C ．84D ．1688．已知正方体1111A B C D A B C D -的棱长为2，E 是棱11D C 的中点，点F 在正方体内部或正方体的表面上，且EF ∥平面11A BC ，则动点F 的轨迹所形成的区域面积是 A ．92B ．23C ．33D ．42第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．双曲线22:13x C y -=的渐近线方程是 ；若抛物线22(0)y px p =>的焦点与 双曲线C 的一个焦点重合，则p = ．10．如图，P 为⊙O 外一点，PA 是⊙O 的切线，A 为切点，割线PBC与⊙O 相交于,B C 两点，且3PC PA =，D 为线段BC 的中点， AD 的延长线交⊙O 于点E ．若1PB =，则PA 的长为______；AD DE ⋅的值是 ．11．已知等边ABC ∆的边长为3，D 是BC 边上一点，若1BD =，则AC AD ⋅uuu r uuu r的值是______．12．已知关于,x y 的不等式组0,,2,2x y x x y x y k≥⎧⎪≥⎪⎨+≤⎪⎪-≥⎩所表示的平面区域D 为三角形区域，则实数k 的取值范围是 ．13．为了响应政府推进“菜篮子”工程建设的号召，某经销商投资60万元建了一个蔬菜生产基地.第一年支出各种费用8万元，以后每年支出的费用比上一年多2万元.每年销售蔬菜的收入为26万元.设()f n 表示前n 年的纯利润（()f n =前n 年的总收入－前n 年的总费用支出－投资额），则()f n =E CODBAP（用n 表示）；从第 年开始盈利.14．在平面直角坐标系O x y 中，以点A (2,0)，曲线21y x =-上的动点B ，第一象限内的点C ，构成等腰直角三角形ABC ,且90A ∠=︒，则线段OC 长的最大值是 ．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）在ABC ∆中，角A ，B ，C 的对边分别是a ，b ，c ，已知1cos 23A =-，3,sin 6sin c A C ==．(Ⅰ)求a 的值；(Ⅱ) 若角A 为锐角，求b 的值及ABC ∆的面积．16．（本小题满分13分）交通指数是交通拥堵指数的简称，是综合反映某区域道路网在某特定时段内畅通或拥堵实际情况的概念性指数值．交通指数范围为(010)，，五个级别规定如下： 交通指数 (0,2)[2,4)[4,6)[6,8)[8,10)级别畅通基本畅通轻度拥堵中度拥堵严重拥堵某人在工作日上班出行每次经过的路段都在同一个区域内，他随机记录了上班的40个工作日早高峰时段(早晨7点至9点)的交通指数(平均值)，其统计结果如直方图所示．（Ⅰ）据此估计此人260个工作日中早高峰 时段（早晨7点至9点）中度拥堵的 天数；（Ⅱ）若此人早晨上班路上所用时间近似为： 畅通时30分钟，基本畅通时35分钟， 轻度拥堵时40分钟，中度拥堵时50 分钟，严重拥堵时70分钟，以直方图 中各种路况的频率作为每天遇到此种路况的概率，求此人上班路上所用时间X 的数学期望．频率组距交通指数值0.25 0.10 0.05 0.152 4 6 8 10 0.20 13 5 7 917．（本小题满分14分）如图1，在等腰梯形ABCD 中，//BC AD ，122BC AD ==，60A ∠=︒， E 为AD 中点，点,O F 分别为,BE DE 的中点．将ABE ∆沿BE 折起到1A BE ∆的位置，使得平面1A BE ⊥平面BCDE （如图2）．（Ⅰ）求证：1A O CE ⊥；（Ⅱ）求直线1A B 与平面1A CE 所成角的正弦值；（Ⅲ）侧棱1A C 上是否存在点P ，使得//BP 平面1A OF ? 若存在，求出11A PA C的值；若不 存在，请说明理由．18． （本小题满分13分）已知函数21()(1)1)ln 2f x x a x a x =-+++-（，a ∈R ． （Ⅰ）当3a =时，求曲线:()C y f x =在点(1,(1))f 处的切线方程；（Ⅱ）当[]1,2x ∈时，若曲线:()C y f x =上的点(,)x y 都在不等式组12,,32x x y y x ⎧⎪≤≤⎪≤⎨⎪⎪≤+⎩所表示的 平面区域内，试求a 的取值范围．ECDBA图1BFOCDA 1E 图219．（本小题满分14分）在平面直角坐标系O x y 中，点000(,)(0)P x y y ≠在椭圆:C 2212x y +=上，过点P 的直线l 的方程为0012x xy y +=． （Ⅰ）求椭圆C 的离心率；（Ⅱ）若直线l 与x 轴、y 轴分别相交于,A B 两点，试求OAB ∆面积的最小值；（Ⅲ）设椭圆C 的左、右焦点分别为1F ，2F ，点Q 与点1F 关于直线l 对称，求证：点2,,Q P F三点共线．20．（本小题满分13分）已知集合311,(22n S k k k n *⎧⎫-⎪⎪=≤≤∈≥⎨⎬⎪⎪⎩⎭N ，且)n *∈N ．若存在非空集合12,,,n S S S L ，使得12n S S S S =U UL U ，且(1,,)i j S S i j n i j =∅≤≤≠I ，并,(1,2,,),i x y S i n x y ∀∈=>L ，都有i x y S -∉，则称集合S 具有性质P ，i S （1,2,,i n =L ）称为集合S 的P 子集． （Ⅰ）当2n =时，试说明集合S 具有性质P ，并写出相应的P 子集S 1,S 2；（Ⅱ）若集合S 具有性质P ，集合T 是集合S 的一个P 子集，设{3|}nT s s T '=+∈，求证：,x y T T '∀∈U ，x y >，都有x y T T '-∉U ； （Ⅲ）求证：对任意正整数2n ≥，集合S 具有性质P ．北京市朝阳区2015-2016学年度第二学期高三年级统一考试数学答案（理工类） 2016．5一、选择题：（满分40分）题号 1 2 3 4 5 6 7 8 答案ABBCDADC二、填空题：（满分30分） 题号 91011121314答案33y x =±，4 3，16 6(,2][0,1)-∞-U21960n n -+-,5221+（注：两空的填空，第一空3分，第二空2分） 三、解答题：（满分80分） 15．（本小题满分13分）解：(Ⅰ) 因为21cos 212sin 3A A =-=-，且 0A <<π，所以6sin 3A =． 因为3,sin 6sin c A C ==，由正弦定理sin sin a cA C=，得66332a c =⋅=⨯=．…………………6分 (Ⅱ) 由6sin ,032A A π=<<得3cos 3A =． 由余弦定理2222cos a b c bc A =+-，得22150b b --=． 解得5b =或3b =-（舍负）． 所以152sin 22ABC S bc A ∆==． …………………13分 解: （Ⅰ）由已知可得：上班的40个工作日中早高峰时段中度拥堵的频率为0.25， 据此估计此人260个工作日早高峰时段（早晨7点至9点）中度拥堵的天数为 260×0.25=65天. ……………………………………………………5分 （Ⅱ）由题意可知X 的可能取值为30,35,40,50,70．且(30)0.05P X ==；(35)0.10P X ==；(40)0.45P X ==； (50)0.25P X ==；(70)0.15P X ==；所以300.05+350.1+400.45+500.25+700.15=46EX =⨯⨯⨯⨯⨯．…………………………………13分17．（本小题满分14分）解：（Ⅰ）如图1，在等腰梯形ABCD 中，由//BC AD ，122BC AD ==，60A ∠=︒，E 为AD 中点，所以ABE ∆为等边三角形．如图2, 因为O 为BE 的中点，所以1A O BE ⊥． 又因为平面1A BE ⊥平面BCDE ， 且平面1A BE I 平面BCDE BE =，所以1A O ⊥平面BCDE ，所以1A O CE ⊥．………4分（Ⅱ）连结OC ，由已知得CB CE =，又O 为BE 的中点，图2所以OC BE ⊥．由（Ⅰ）知1A O ⊥平面BCDE ， 所以11,A O BE A O OC ⊥⊥， 所以1,,OA OB OC 两两垂直．以O 为原点，1,,OB OC OA 分别为,,x y z 轴建立空间直角坐标系（如图）．因为2BC =，易知13OA OC ==．所以1(003),(100),(030),(100)A B C E -，，，，，，，，， 所以111(103),(033),(103)A B AC A E =-=-=--u u u r u u u r u u u r，，，，，，． 设平面1A CE 的一个法向量为(,,)x y z =n ，ECDBA图1A 1xy z FOB CDEP CBFODA 1E由 110,0 AC A E ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r n n 得330, 30.y z x z ⎧-=⎪⎨--=⎪⎩ 即0, 30. y z x z -=⎧⎪⎨+=⎪⎩取1z =，得(3,1,1)=-n ．设直线1A B 与平面1A CE 所成角为θ，则133315sin cos ,5255A B θ--=〈〉===⨯u u u r n ． 所以直线1A B 与平面1A CE 所成角的正弦值为155． …………………9分 （Ⅲ）假设在侧棱1A C 上存在点P ，使得//BP 平面1A OF ．设11A P AC λ=u u u r u u u r ，[0,1]λ∈．因为1111BP BA A P BA AC λ=+=+u u u r u u u r u u u r u u u r u u u r， 所以(103)(033)(1,3,33)BP λλλ=-+-=--u u u r，，，，． 易证四边形BCDE 为菱形，且CE BD ⊥，又由（Ⅰ）可知，1A O CE ⊥，所以CE ⊥平面1A OF ．所以(1,3,0)CE =--u u u r为平面1A OF 的一个法向量．由(1,3,33)(1,3,0)130BP CE λλλ⋅=--⋅--=-=u u u r u u u r ，得1[0,1]3λ=∈．所以侧棱1A C 上存在点P ，使得//BP 平面1A OF ，且1113A P A C =． …………14分 18．（本小题满分13分） 解：（Ⅰ）当3a =时, 21()42ln 2f x x x x =-+-，0x >． 2()4f x x x'=-+-．则(1)1421f '=-+-=，而17(1)422f =-+=． 所以曲线C 在点(1,(1)f )处的切线方程为712y x -=-，即2250x y -+=．…………………………………………………………………………4分（Ⅱ）依题意当[]1,2x ∈时，曲线C 上的点(),x y 都在不等式组12,,32x x y y x ⎧⎪≤≤⎪≤⎨⎪⎪≤+⎩所表示的平面区域内，等价于当12x ≤≤时，3()2x f x x ≤≤+恒成立． 设()()g x f x x =-211)ln 2x ax a x （=-++-，[]1,2x ∈． 所以21(1)()=+=a x ax a g x x a+x x ---++-'(1)(1))=x x a x---(-． （1）当11a -≤，即2a ≤时，当[]1,2x ∈时，()0g x '≤，()g x 为单调减函数，所以(2)()(1)g g x g ≤≤． 依题意应有131,222221ln20,()()()g a g a a ⎧=-≤⎪⎨⎪=-++-≥⎩ 解得21a a ,.≤⎧⎨≥⎩所以12a ≤≤．（2）若 112a <-<，即23a <<时，当[)1,1x a ∈-，()0g x '≥，()g x 为单调增函 数，当x ∈(]1,2a -，()0g x '<，()g x 为单调减函数．由于3(1)2g >，所以不合题意． （3）当12a -≥，即3a ≥时，注意到15(1)22g a =-≥，显然不合题意． 综上所述，12a ≤≤． …………………………………………13分19．（本小题满分14分） 解：（Ⅰ）依题意可知2a =，211c =-=，所以椭圆C 离心率为1222e ==． …………… 3分 （Ⅱ）因为直线l 与x 轴，y 轴分别相交于,A B 两点，所以000,0x y ≠≠． 令0y =，由0012x x y y +=得02x x =，则02(,0)A x ．令0x =，由0012x x y y +=得01y y =，则01(0,)B y ． 所以OAB ∆的面积0000112122OAB S OA OB x y x y ∆===． 因为点00(,)P x y 在椭圆:C 2212x y +=上，所以220012x y +=． 所以2002001222x y x y =+≥．即0022x y ≤，则0012x y ≥． 所以001122OAB S OA OB x y ∆==≥． 当且仅当22002x y =，即0021,2x y =±=±时，OAB ∆面积的最小值为2． … 9分（Ⅲ）①当00x =时，(0,1)P ±．当直线:1l y =时，易得(1,2)Q -，此时21F P k =-，21F Q k =-．因为22F Q F P k k =，所以三点2,,Q P F 共线． 同理，当直线:1l y =-时，三点2,,Q P F 共线．②当00x ≠时，设点(,)Q m n ，因为点Q 与点1F 关于直线l 对称，所以000011,22202() 1.1212x m n y n x m y -⎧⋅+⋅=⎪⎪⎪⎨-⎪⋅-=--⎪+⎪⎩整理得000000240,220.x m y n x y m x n y +--=⎧⎨-+=⎩解得220002200000220044,448.4x x y m y x x y y n y x ⎧+-=⎪+⎪⎨+⎪=⎪+⎩所以点22000000222200004448(,)44x x y x y y Q y x y x +-+++．又因为200(1,)F P x y =-u u u u r ，220000002222200004448(1,)44x x y x y y F Q y x y x +-+=-++u u u u r ， 且 22200000000000002222220000004448(48)(48)(1)(1)(1)444x x y x y y x y x x y x y y x y x y x +-+--+--⋅-⋅-=⋅+++2200000220048(448)4x y x x y y x --+-=⋅+ 222200000002222220000008484(2)84280444y x y x y y y y x y x y x --+-++-⨯+=⋅=⋅=⋅=+++． 所以2//F P u u u u r 2F Q u u u u r ．所以点2,,Q P F 三点共线．综上所述，点2,,Q P F 三点共线． …………………………………14分 20．（本小题满分13分）证明：（Ⅰ）当2n =时，{1,2,3,4}S =，令1{1,4}S =，2{2,3}S =,则12S S S =U , 且对,(1,2),i x y S i x y ∀∈=>，都有i x y S -∉，所以S 具有性质P ．相应的P 子集为1{1,4}S =，2{2,3}S =． ………… 3分 （Ⅱ）①若31,(1)2n x y T y x -∈≤<≤,由已知x y T -∉, 又31132n n x y --≤-<,所以x y T '-∉．所以'x y T T -∉U ． ②若,x y T '∈,可设3,3n nx s y r =+=+，,r s T ∈,且3112n r s -≤<≤， 此时31(3)(3)132n n nn x y s r s r --=+-+=-≤-<． 所以'x y T -∉，且x y s r T -=-∉．所以x y T T '-∉U ．③若y T ∈, 3nx s T '=+∈,s T ∈， 则313331(3)()3(1)3222n n n n nn x y s y s y -+--=+-=-+≥-+=>, 所以x y T -∉．又因为,y T s T ∈∈，所以s y T -∉．所以(3)()3n n x y s y s y T '-=+-=-+∉．所以'x y T T -∉U ．综上，对于,'x y T T ∀∈U ，x y >，都有'x y T T -∉U ． …………… 8分 （Ⅲ）用数学归纳法证明．（1）由（Ⅰ）可知当2n =时，命题成立，即集合S 具有性质P ．（2）假设n k =(2k ≥)时，命题成立．即1231{1,2,3,,}2k k S S S S -==L U UL U ， 且(1,,)i j S S i j n i j =∅≤≤≠I ，,(1,2,,),i x y S i k x y ∀∈=>L ，都有i x y S -∉． 那么 当1n k =+时，记{3|}k i i S s s S '=+∈,，并构造如下 k +1个集合：111S S S '''=U ,222S S S '''=U ,,kk k S S S '''=U ， 1313131{1,2,,21}222k k k k S +---''=++⨯+L ， 显然()i j S S i j ''''=∅≠I ． 又因为131313122k k +--=⨯+，所以112131{1,2,3,,}2k k k S S S S ++-''''''''=U UL U U L ． 下面证明 ¢¢S i 中任意两个元素之差不等于¢¢S i 中的任一元素(1,2,,1)i k =+L ． ①若两个元素13131,22k k k r s S +--''++∈,31112k r s -≤<≤+, 则313131()()222k k k s r s r ---+-+=-≤, 所以13131()()22k k k s r S +--''+-+∉． ②若两个元素都属于i i i S S S '''=U (1)i k ≤≤,由（Ⅱ）可知，i S ''中任意两个元素之差不等于i S ''中的任一数(1,2,,1)i k =+L ． 从而，1n k =+时命题成立．综上所述，对任意正整数2n ≥，集合S 具有性质P ．………………………13分。

北京市朝阳区高三年级第一次综合练习数学试卷（理工类） 2016．3（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项． 1． i 为虚数单位，复数2i 1i+= A ．1i - B ．1i -- C ．1i -+ D ．1i +2． 已知全集U =R ，函数ln(1)y x =-的定义域为M ，集合{}20N x x x =-<，则下列结论正确的是 A ．M N N = B ．()UMN =∅C ．MN U = D ．()U M N ⊆3．>e e ab>”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 4． 执行如图所示的程序框图，输出的S 值为 A ．42 B ．19 C ．8 D ．35．在ABC ∆中，角A ，B ，C 的对边分别为,,.a b c若222()tan a c b B +-=，则角B 的值为A ． 3πB ． 6πC ． 233ππ或 D ． 566ππ或(第4题图)6．某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误．．的是 A. 收入最高值与收入最低值的比是3:1B. 结余最高的月份是7月C.1至2月份的收入的变化率与4至5月份的收入的变化率相同D. 前6个月的平均收入为40万元 （注：结余=收入-支出）7．某三棱锥的三视图如图所示，则该三棱锥的体积是A ．13 B ．12C ．1D ．328．若圆222(1)x y r+-=与曲线(1)1x y -=的没有公共点，则半径r 的取值范围是 A．0r << B．0r <<C．0r << D ．0r <<第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．月23415689 10 7111258(第7题图)侧视图俯视图9． 二项式251()x x+的展开式中含4x 的项的系数是 （用数字作答）．10．已知等差数列}{n a (n *∈N )中，11=a ，47a =，则数列}{n a 的通项公式n a = ；2610410n a a a a +++++=______．11．在直角坐标系xOy 中，曲线1C 的方程为222x y +=，曲线2C 的参数方程为2,(x t t y t=-⎧⎨=⎩为参数)．以原点O 为极点，x 轴非负半轴为极轴，建立极坐标系，则曲 线1C 与2C 的交点的极坐标．．．为 ． 12．不等式组0,,290x y x x y ≥⎧⎪≤⎨⎪+-≤⎩所表示的平面区域为D ．若直线(1)y a x =+与区域D 有公共点，则实数a 的取值范围是 ． 13．已知M 为ABC ∆所在平面内的一点，且14AM AB nAC =+．若点M 在ABC ∆的内部(不含边界)，则实数n 的取值范围是____．14．某班主任在其工作手册中，对该班每个学生用十二项能力特征加以描述．每名学生的第i （1,2,,12i =）项能力特征用i x 表示，0,1i i x i ⎧=⎨⎩如果某学生不具有第项能力特征，，如果某学生具有第项能力特征.若学生,A B 的十二项能力特征分别记为1212(,,,)A a a a =，1212(,,,)B b b b =，则,A B两名学生的不同能力特征项数为 （用,i i a b 表示）．如果两个同学不同能力特征项数不少于7，那么就说这两个同学的综合能力差异较大．若该班有3名学生两两综合能力差异较大，则这3名学生两两不同能力特征项数总和的最小值为 ． 三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）已知函数21()sin 22x f x x ωω=+，0ω>． （Ⅰ）若1ω=，求()f x 的单调递增区间；（Ⅱ）若()13f π=，求()f x 的最小正周期T 的表达式并指出T 的最大值．16．（本小题满分13分）为了解学生暑假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表．（Ⅰ）从这班学生中任选一名男生，一名女生，求这两名学生阅读名著本数之和为4的概率？（Ⅱ）若从阅读名著不少于4本的学生中任选4人，设选到的男学生人数为X ，求随机变量X 的分布列和数学期望；（Ⅲ）试判断男学生阅读名著本数的方差21s 与女学生阅读名著本数的方差22s 的大小（只需 写出结论）．17．（本小题满分14分）如图，在直角梯形11AA B B 中，190A AB ∠=︒，11//A B AB ，11122AB AA A B ===．直角梯形11AAC C 通过直角梯形11AA B B 以直线1AA 为轴旋转得到，且使得平面11AA C C ⊥平面11AA B B ．M 为线段BC 的中点，P 为线段1BB 上的动点．（Ⅰ）求证：11A C AP ⊥；（Ⅱ）当点P 是线段1BB 中点时，求二面角P AM B --的余弦值；（Ⅲ）是否存在点P ，使得直线1A C //平面AMP ？请说明理由．18．（本小题满分13分）已知函数()f x =ln ,x a x a +∈R ． （Ⅰ）求函数()f x 的单调区间；AMPCBA 1C 1B 1（Ⅱ）当[]1,2x ∈时，都有()0f x >成立，求a 的取值范围；（Ⅲ）试问过点(13)P ，可作多少条直线与曲线()y f x =相切？并说明理由．19．（本小题满分14分）已知点P 和椭圆:C 22142x y +=． （Ⅰ）设椭圆的两个焦点分别为1F ，2F ，试求12PF F ∆的周长及椭圆的离心率；（Ⅱ）若直线:l 20(0)y m m -+=≠与椭圆C 交于两个不同的点A ，B ，直线PA ，PB 与x轴分别交于M ，N 两点，求证：PM PN =．20．（本小题满分13分）已知等差数列}{n a 的通项公式31()n a n n *=-∈N .设数列{}n b 为等比数列,且n n k b a =.（Ⅰ）若11=2b a =,且等比数列{}n b 的公比最小， （ⅰ）写出数列{}n b 的前4项； （ⅱ）求数列{}n k 的通项公式；（Ⅱ）证明：以125b a ==为首项的无穷等比数列{}n b 有无数多个.北京市朝阳区2015-2016学年度第二学期高三年级统一考试数学答案（理工类） 2016．3一、选择题：（满分40分）二、填空题：（满分30分）（注：两空的填空，第一空3分，第二空2分） 三、解答题：（满分80分） 15．（本小题满分13分） 解：（Ⅰ）当1ω=时，21()sin 22x f x x =1sin 2x x =+ sin()3x π=+．令22,232k x k k ππππ-≤+≤π+∈Z ．解得22,66k x k k 5πππ-≤≤π+∈Z ． 所以()f x 的单调递增区间是[2,2],66k k k 5πππ-π+∈Z .……………………7分 （Ⅱ）由21()sin 22x f x x ωω=+ 1sin 2x x ωω=+ sin()3x ωπ=+．因为()13f π=，所以sin()133ωππ+=．则2332n ωπππ+=π+，n ∈Z ． 解得162n ω=+．又因为函数()f x 的最小正周期2T ωπ=，且0ω>，所以当ω12=时，T 的最大值为4π． ………………………………………13分 16．（本小题满分13分）解：（Ⅰ）设事件A ：从这个班级的学生中随机选取一名男生，一名女生，这两名学生阅读本数之和为4 ． 由题意可知，13+41()128P A ⨯⨯=⨯4分（Ⅱ）阅读名著不少于4本的学生共8人，其中男学生人数为4人，故X 的取值为0,1,2,3,4．由题意可得44481(0)70C P X C ===； 134448168(1)7035C C P X C ====；2244483618(2)7035C C P X C ====； 314448168(3)7035C C P X C ====； 44481(4)70C P X C ===． 所以随机变量X 的分布列为随机变量X 的均值0123427070707070EX =⨯+⨯+⨯+⨯+⨯=．…………10分（Ⅲ）21s >22s ．…………………………………………………………………………13分17．（本小题满分14分）解：（Ⅰ）由已知1190A AB A AC ∠=∠=︒，且平面11AA C C ⊥平面11AA B B ，所以90BAC ∠=︒，即AC AB ⊥． 又因为1AC AA ⊥且1ABAA A =，所以AC ⊥平面11AA B B ．由已知11//A C AC ，所以11A C ⊥平面11AA B B ． 因为AP ⊂平面11AA B B ，所以11AC AP ⊥．…………………………………………………………………………4分 （Ⅱ）由（Ⅰ）可知1,,AC AB AA 两两垂直．分别以1,,AC AB AA 为x 轴、y 轴、z 轴建立空间直角坐标系如图所示． 由已知 11111222AB AC AA A B AC =====， 所以(0,0,0),(0,2,0),(2,0,0),A B C 1(0,1,2)B ，1(0,0,2)A ．因为M 为线段BC 的中点，P 为线段1BB 的中点，所以3(1,1,0),(0,,1)2M P ．易知平面ABM 的一个法向量(0,0,1)=m ． 设平面APM 的一个法向量为(,,)x y z =n ，由 0,0,AM AP ⎧⋅=⎪⎨⋅=⎪⎩n n 得0, 30. 2x y y z +=⎧⎪⎨+=⎪⎩取2y =，得(2,2,3)=--n ．由图可知，二面角P AM B --的大小为锐角，所以cos ,⋅〈〉===⋅m n m n m n．所以二面角P AM B --．………………………………9分 （Ⅲ）存在点P ，使得直线1A C //平面AMP ．设111(,,)P x y z ，且1BP BB λ=，[0,1]λ∈，则111(,2,)(0,1,2)x y z λ-=-， 所以1110,2,2x y z λλ==-=．所以(0,2,2)AP λλ=-． 设平面AMP 的一个法向量为0000(,,)x y z =n ，由 000,0,AM AP ⎧⋅=⎪⎨⋅=⎪⎩n n 得00000, (2)20. x y y z λλ+=⎧⎨-+=⎩取01y =，得02(1,1,)2λλ-=-n （显然0λ=不符合题意）．又1(2,0,2)AC =-，若1A C //平面AMP ，则10AC ⊥n ． 所以10220AC λλ-⋅=--=n ．所以23λ=． 所以在线段1BB 上存在点P ，且12BPPB =时，使得直线1A C //平面AMP ．…………14分 18．（本小题满分13分）解：（Ⅰ）函数()f x 的定义域为{}0x x >．()1a x af x x x+'=+=． （1）当0a ≥时，()0f x '>恒成立，函数()f x 在(0,)+∞上单调递增； （2）当0a <时， 令()0f x '=，得x a =-．当0x a <<-时，()0f x '<，函数()f x 为减函数； 当x a >-时，()0f x '>，函数()f x 为增函数．综上所述，当0a ≥时，函数()f x 的单调递增区间为(0,)+∞．当0a <时，函数()f x 的单调递减区间为(0,)a -，单调递增区间为(+)a -∞，． ……………………………………………………………………………………4分 （Ⅱ）由（Ⅰ）可知，（1）当1a -≤时，即1a ≥-时，函数()f x 在区间[]1,2上为增函数，所以在区间[]1,2上，min ()(1)1f x f ==，显然函数()f x 在区间[]1,2上恒大于零； （2）当12a <-<时，即21a -<<-时，函数()f x 在[)1a -，上为减函数，在(],2a - 上为增函数，所以min ()()ln()f x f a a a a =-=-+-．依题意有min ()ln()0f x a a a =-+->，解得e a >-，所以21a -<<-． （3）当2a -≥时，即2a ≤-时，()f x 在区间[]1,2上为减函数，所以min ()(2)2+ln 2f x f a ==．依题意有min ()2+ln 20f x a =>，解得2ln 2a >-，所以22ln 2a -<≤-． 综上所述，当2ln 2a >-时，函数()f x 在区间[]1,2上恒大于零．………………8分 （Ⅲ）设切点为000,ln )x x a x +（，则切线斜率01a k x =+， 切线方程为0000(ln )(1)()ay x a x x x x -+=+-． 因为切线过点(1,3)P ，则00003(ln )(1)(1)ax a x x x -+=+-． 即001(ln 1)20a x x +--=． ………………① 令1()(ln 1)2g x a x x =+-- (0)x >，则 2211(1)()()a x g x a x x x -'=-=． （1）当0a <时，在区间(0,1)上，()0g x '>， ()g x 单调递增；在区间(1,)+∞上，()0g x '<，()g x 单调递减， 所以函数()g x 的最大值为(1)20g =-<． 故方程()0g x =无解，即不存在0x 满足①式． 因此当0a <时，切线的条数为0．（2）当0a >时, 在区间(0,1)上，()0g x '<，()g x 单调递减，在区间(1,)+∞上，()0g x '>，()g x 单调递增， 所以函数()g x 的最小值为(1)20g =-<．取21+1ee ax =>，则221112()(1e 1)2e 0aag x a a a----=++--=>．故()g x 在(1,)+∞上存在唯一零点．取2-1-21e<e ax =，则221122()(1e 1)2e 24a a g x a a a a ++=--+--=--212[e 2(1)]aa a+=-+．设21(1)t t a=+>，()e 2t u t t =-，则()e 2t u t '=-． 当1t >时，()e 2e 20t u t '=->->恒成立．所以()u t 在(1,)+∞单调递增，()(1)e 20u t u >=->恒成立．所以2()0g x >． 故()g x 在(0,1)上存在唯一零点．因此当0a >时，过点P (13)，存在两条切线．（3）当0a =时，()f x x =，显然不存在过点P (13)，的切线．综上所述，当0a >时，过点P (13)，存在两条切线；当0a ≤时，不存在过点P (13)，的切线．…………………………………………………13分19．（本小题满分14分）解：(Ⅰ)由题意可知，24a =，22b =，所以22c =．因为P 是椭圆C 上的点，由椭圆定义得124PF PF +=．所以12PF F ∆的周长为4+．易得椭圆的离心率=2c e a =．………………………………………………………4分 (Ⅱ)由2220,1,42y m x y -+=⎨+=⎪⎩得22480x m ++-=． 因为直线l 与椭圆C 有两个交点，并注意到直线l 不过点P ，所以22844(8)0,0.m m m ⎧-⨯->⎨≠⎩解得40m -<<或04m <<． 设11(,)A x y ，22(,)B x y，则122x x +=-，21284m x x -=, 112m y +=，222m y +=． 显然直线PA 与PB 的斜率存在，设直线PA 与PB 的斜率分别为1k ，2k ，则12k k +=211)(1)(x x -+-====2=220==． 因为120k k +=，所以PMN PNM ∠=∠． 所以PM PN =． ………………………………………………………14分 20．（本小题满分13分）解：（Ⅰ）观察数列}{n a 的前若干项：2，5，8，11，14，17，20，23，26，29，32，35，…. 因为数列}{n a 是递增的整数数列，且等比数列以2为首项，显然最小公比不能是52，最小公比是4.（ⅰ）以2为首项,且公比最小的等比数列的前四项是2，8，32，128.（ⅱ）由（ⅰ）可知12b =，公比4q =，所以124n n b -=⋅.又31n n k n b a k ==-，所以13124,n n k n -*-=⋅∈N ， 即11(241),3n n k n -*=⋅+∈N . 再证n k 为正整数.显然11k =为正整数，2n ≥时，1222111(2424)24(41)2433n n n n n n k k ------=⋅-⋅=⋅⋅-=⋅， 即2124(2)n n n k k n --=+⋅≥，故11(241),3n n k n -*=⋅+∈N 为正整数. 所以，所求通项公式为11(241),3n n k n -*=⋅+∈N . ……………………………………………………………………………6分（Ⅱ）设数列{}n c 是数列}{n a 中包含的一个无穷等比数列，且115k c a ==，22231k c a k ==-，所以公比2315k q -=.因为等比数列{}n c 各项为整数，所以q 为整数. 取252k m =+（m *∈N ），则13+=m q ，故15(31)n n c m -=⋅+.只要证15(31)n n c m -=⋅+是数列}{n a 的项，即证31n k -15(31)n m -=⋅+. 只要证11[5(31)1]3n n k m -=++()n *∈N 为正整数，显然12k =为正整数. 又2n ≥时，12215[(31)(31)]5(31)3n n n n n k k m m m m -----=+-+=+， 即215(31)n n n k k m m --=++，又因为12k =，25(31)n m m -+都是正整数， 故2n ≥时，n k 也都是正整数.所以数列{}n c 是数列}{n a 中包含的无穷等比数列，其公比13+=m q 有无数个不同的取值，对应着不同的等比数列，故数列}{n a 所包含的以52=a 为首项的不同无穷等比数列有无数多个.…………………………………………………………………………………………13分。

2015-2016学年北京市朝阳区高三（上）期末数学试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．已知集合M={x|﹣1＜x＜1}，，则M∩N=（）A．{x|0≤x＜1} B．{x|0＜x＜1} C．{x|x≥0} D．{x|﹣1＜x≤0}2．复数z=i（1+i）（i是虚数单位）在复平面内所对应点的坐标为（）A．（1，1）B．（﹣1，﹣1）C．（1，﹣1）D．（﹣1，1）3．执行如图所示的程序框图，则输出的i值为（）A．3 B．4 C．5 D．64．在一段时间内有2000辆车通过高速公路上的某处，现随机抽取其中的200辆进行车速统计，统计结果如下面的频率分布直方图所示．若该处高速公路规定正常行驶速度为90km/h～120km/h，试估计2000辆车中，在这段时间内以正常速度通过该处的汽车约有（）A．30辆B．300辆C．170辆D．1700辆5．“a＞1”是“函数f（x）=a•x+cosx在R上单调递增”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件6．已知点Q（2，0）及抛物线x2=4y上一动点P（x，y），则y+|PQ|的最小值是（）A．B．1 C．2 D．37．某四棱锥的三视图如图所示，则该四棱锥的侧面积是（）A．27 B．30 C．32 D．368．设函数f（x）的定义域D，如果存在正实数m，使得对任意x∈D，都有f（x+m）＞f（x），则称f（x）为D上的“m型增函数”．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x﹣a|﹣a（a∈R）．若f（x）为R上的“20型增函数”，则实数a的取值范围是（）A．a＞0 B．a＜5 C．a＜10 D．a＜20二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．函数y=2sin（2x+）+1的最小正周期是，最小值是．10．若x，y满足约束条件则z=x+y的最大值为．11．在各项均为正数的等比数列{a n}中，若a2=2，则a1+2a3的最小值是．12．甲、乙、丙、丁四名同学和一名老师站成一排合影留念．要求老师必须站在正中间，甲同学不与老师相邻，则不同站法种数为．13．已知A，B为圆C：（x﹣m）2+（y﹣n）2=9（m，n∈R）上两个不同的点（C为圆心），且满足，则|AB|= ．14．已知点O在△ABC的内部，且有=，记△AOB，△BOC，△AOC的面积分别为S△AOB，S△BOC，S△AOC．若x=y=z=1，则S△AOB：S△BOC：S△AOC= ；若x=2，y=3，z=4，则S△AOB：S△BOC：S△AOC= ．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．某中学高一年级共8个班，现从高一年级选10名同学组成社区服务小组，其中高一（1）班选取3名同学，其它各班各选取1名同学．现从这10名同学中随机选取3名同学，到社区老年中心参加“尊老爱老”活动（每位同学被选到的可能性相同）．（Ⅰ）求选出的3名同学来自不同班级的概率；（Ⅱ）设X为选出同学中高一（1）班同学的人数，求随机变量X的分布列和数学期望．16．如图，在△ABC中，点D在BC边上，，．（Ⅰ）求sin∠C的值；（Ⅱ）若BD=5，求△ABD的面积．17．如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠DAB=60°．点E是棱PC的中点，平面ABE与棱PD交于点F．（Ⅰ）求证：AB∥EF；（Ⅱ）若PA=PD=AD，且平面PAD⊥平面ABCD，求平面PAF与平面AFE所成的锐二面角的余弦值．18．已知函数f（x）=ax+lnx，其中a∈R．（Ⅰ）若f（x）在区间上为增函数，求a的取值范围；（Ⅱ）当a=﹣e时，（ⅰ）证明：f（x）+2≤0；（ⅱ）试判断方程是否有实数解，并说明理由．19．已知圆O：x2+y2=1的切线l与椭圆C：x2+3y2=4相交于A，B两点．（Ⅰ）求椭圆C的离心率；（Ⅱ）求证：OA⊥OB；（Ⅲ）求△OAB面积的最大值．20．已知有穷数列：的各项均为正数，且满足条件：①a1=a k；②．（Ⅰ）若k=3，a1=2，求出这个数列；（Ⅱ）若k=4，求a1的所有取值的集合；（Ⅲ）若k是偶数，求a1的最大值（用k表示）．2015-2016学年北京市朝阳区高三（上）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．已知集合M={x|﹣1＜x＜1}，，则M∩N=（）A．{x|0≤x＜1} B．{x|0＜x＜1} C．{x|x≥0} D．{x|﹣1＜x≤0}【考点】交集及其运算．【分析】求出N中不等式的解集确定出N，找出M与N的交集即可．【解答】解：由N中不等式变形得：x（x﹣1）≤0，且x≠1，解得：0≤x＜1，即N={x|0≤x＜1}，∵M={x|﹣1＜x＜1}，∴M∩N={x|0≤x＜1}，故选：A．2．复数z=i（1+i）（i是虚数单位）在复平面内所对应点的坐标为（）A．（1，1）B．（﹣1，﹣1）C．（1，﹣1）D．（﹣1，1）【考点】复数代数形式的乘除运算．【分析】先将z=i（1+i）化简，从而判断即可．【解答】解：z=i（1+i）=﹣1+i，∴复数z=i（1+i）（i是虚数单位）在复平面内所对应点的坐标为：（﹣1，1），故选：D．3．执行如图所示的程序框图，则输出的i值为（）A．3 B．4 C．5 D．6【考点】程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的m，i的值，当m=0时满足条件m=0，退出循环，输出i的值为4．【解答】解：模拟执行程序框图，可得m=1，i=1，m=1×（2﹣1）+1=2，i=2，不满足条件m=0，m=2×（2﹣2）+1=1，i=3，不满足条件m=0，m=1×（2﹣3）+1=0，i=4，满足条件m=0，退出循环，输出i的值为4．故选：B．4．在一段时间内有2000辆车通过高速公路上的某处，现随机抽取其中的200辆进行车速统计，统计结果如下面的频率分布直方图所示．若该处高速公路规定正常行驶速度为90km/h～120km/h，试估计2000辆车中，在这段时间内以正常速度通过该处的汽车约有（）A．30辆B．300辆C．170辆D．1700辆【考点】频率分布直方图．【分析】由频率分布直方图求出在这段时间内以正常速度通过该处的汽车的频率，由此能估计2000辆车中，在这段时间内以正常速度通过该处的汽车约有多少辆．【解答】解：由频率分布直方图得：在这段时间内以正常速度通过该处的汽车的频率为（0.03+0.035+0.02）×10=0.85，∴估计2000辆车中，在这段时间内以正常速度通过该处的汽车约有：2000×0.85=1700（辆）．故选：D．5．“a＞1”是“函数f（x）=a•x+cosx在R上单调递增”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分条件和必要条件的定义进行判断即可．【解答】解：若函数f（x）=a•x+cosx在R上单调递增，则f′（x）≥0恒成立，即f′（x）=a﹣sinx≥0，即a≥sinx，∵﹣1≤sinx≤1，∴a≥1，则“a＞1”是“函数f（x）=a•x+cosx在R上单调递增”充分不必要条件，故选：A．6．已知点Q（2，0）及抛物线x2=4y上一动点P（x，y），则y+|PQ|的最小值是（）A．B．1 C．2 D．3【考点】抛物线的简单性质．【分析】抛物线的准线是y=﹣1，焦点F（0，1）．设P到准线的距离为d，利用抛物线的定义得出：y+|PQ|=d﹣1+|PQ|=|PF|+|PQ|﹣1≥|FQ|﹣1，利用当且仅当F、Q、P共线时取最小值，从而得出故y+|PQ|的最小值．【解答】解：抛物线x2=4y的准线是y=﹣1，焦点F（0，1）．设P到准线的距离为d，则y+|PQ|=d﹣1+|PQ|=|PF|+|PQ|﹣1≥|FQ|﹣1=3﹣1=2（当且仅当F、Q、P共线时取等号）故y+|PQ|的最小值是2．故选C．7．某四棱锥的三视图如图所示，则该四棱锥的侧面积是（）A．27 B．30 C．32 D．36【考点】由三视图求面积、体积．【分析】几何体为侧放的四棱锥，作出直观图，代入数据计算四个侧面的面积．【解答】解：由三视图可知几何体为四棱锥，作出直观图如图所示，其中底面ABCD是边长为3的正方形，DA⊥平面PAB，AP⊥平面ABCD，AP=4，∴CD⊥平面PAD，PB=PD=5，∴S△ADP==6，S△ABP==6，S△CDP==，S△CBP==．∴四棱锥的侧面积S=6+6++=27．故选A．8．设函数f（x）的定义域D，如果存在正实数m，使得对任意x∈D，都有f（x+m）＞f（x），则称f（x）为D上的“m型增函数”．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x﹣a|﹣a（a∈R）．若f（x）为R上的“20型增函数”，则实数a的取值范围是（）A．a＞0 B．a＜5 C．a＜10 D．a＜20【考点】函数的值．【分析】由已知得f（x）=，f（x+20）＞f（x），由此能求出实数a的取值范围．【解答】解：∵函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x﹣a|﹣a（a∈R），∴f（x）=，∵f（x）为R上的“20型增函数”，∴f（x+20）＞f（x），当x=0时，|20﹣a|﹣a＞0，解得a＜10．∴实数a的取值范围是a＜10．故选：C．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．函数y=2sin（2x+）+1的最小正周期是π，最小值是﹣1 ．【考点】正弦函数的图象．【分析】由条件利用正弦函数的周期性和最小值，得出结论．【解答】解：函数y=2sin（2x+）+1的最小正周期是=π，最小值为﹣2+1=﹣1，故答案为：π，﹣1．10．若x，y满足约束条件则z=x+y的最大值为 4 ．【考点】简单线性规划．【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．【解答】解：由约束条件作出可行域如图，联立，解得A（3，1），化目标函数z=x+y为y=﹣x+z．由图可知，当直线y=﹣x+z过A时，直线在y轴上的截距最大，z有最大值为4．故答案为：4．11．在各项均为正数的等比数列{a n}中，若a2=2，则a1+2a3的最小值是4．【考点】等比数列的通项公式；数列的函数特性．【分析】由基本不等式可得，a1+2a3≥2=，结合已知即可求解【解答】解：∵a2=2，且a n＞0由基本不等式可得，a1+2a3≥2==4即最小值为故答案为：12．甲、乙、丙、丁四名同学和一名老师站成一排合影留念．要求老师必须站在正中间，甲同学不与老师相邻，则不同站法种数为12 ．【考点】计数原理的应用．【分析】由题意，甲必须站两端，有2种方法，其余3名同学，有=6种方法，根据乘法原理，可得结论．【解答】解：由题意，甲必须站两端，有2种方法，其余3名同学，有=6种方法，根据乘法原理，共有2×6=12种方法．故答案为：12．13．已知A，B为圆C：（x﹣m）2+（y﹣n）2=9（m，n∈R）上两个不同的点（C为圆心），且满足，则|AB|= 4 ．【考点】平面向量数量积的运算．【分析】求得圆的圆心和半径，运用向量的减法运算和数量积的性质：向量模的平方即为向量的平方，求得|+|2+||2=36，即可得到所求值．【解答】解：由圆C：（x﹣m）2+（y﹣n）2=9可得，圆心C（m，n），半径为3，由题意可得||=||=3，由|+|2+||2=|+|2+|﹣|2=2+2+2•+2+2﹣2•=2（2+2）=2（32+32）=36，由，可得||2=16，即有||=4．故答案为：4．14．已知点O 在△ABC 的内部，且有=，记△AOB ，△BOC ，△AOC 的面积分别为S △AOB ，S △BOC ，S △AOC ．若x=y=z=1，则S △AOB ：S △BOC ：S △AOC = 1：1：1 ；若x=2，y=3，z=4，则S △AOB ：S △BOC ：S △AOC = 4：2：3 ． 【考点】向量的线性运算性质及几何意义．【分析】（1）由=，得O 是△ABC 的重心，故S △AOB =S △BOC =S △AOC ，得出答案；（2）延长OA ，OB ，OC ，使OD=2OA ，OE=3OB ，OF=4OC ，结合已知可得O 是△DEF 的重心，故△DOE ，△EOF ，△DOF 的面积相等，进而得到答案．【解答】解：若=，则O 是△ABC 的重心，∴S △AOB =S △BOC =S △AOC =S △ABC ，∴S △AOB ：S △BOC ：S △AOC =1：1：1．若2+3+4=，延长OA ，OB ，OC ，使OD=2OA ，OE=3OB ，OF=4OC ，如图所示：则，∴O 是△DEF 的重心，∴S △DOE =S △EOF =S △DOF ．∴S △AOB ==×OD ×sin ∠AOB=S △DOE ，S △BOC ==OFsin ∠BOC=S △EOF ，S △AOC ==OFsin ∠BOC=S △DOF ，∴S △AOB ：S △BOC ：S △AOC =：：=4：2：3．故答案为1：1：1，4：2：3．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．某中学高一年级共8个班，现从高一年级选10名同学组成社区服务小组，其中高一（1）班选取3名同学，其它各班各选取1名同学．现从这10名同学中随机选取3名同学，到社区老年中心参加“尊老爱老”活动（每位同学被选到的可能性相同）．（Ⅰ）求选出的3名同学来自不同班级的概率；（Ⅱ）设X为选出同学中高一（1）班同学的人数，求随机变量X的分布列和数学期望．【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．【分析】（Ⅰ）设“选出的3名同学来自不同班级”为事件A，利用排列组合知识能求出选出的3名同学来自班级的概率．（Ⅱ）随机变量X的所有可能值为0，1，2，3，分别求出相应的概率，由此能求出随机变量X的分布列和随机变量X的数学期望E（X）．【解答】（本小题满分13分）解：（Ⅰ）设“选出的3名同学来自不同班级”为事件A，则P（A）==．所以选出的3名同学来自班级的概率为．…（Ⅱ）随机变量X的所有可能值为0，1，2，3，P（X=0）==，P（X=1）==，P（X=2）==，P（X=3）==，∴随机变量X的分布列是随机变量X的数学期望E（X）==．16．如图，在△ABC中，点D在BC边上，，．（Ⅰ）求sin∠C的值；（Ⅱ）若BD=5，求△ABD的面积．【考点】正弦定理．【分析】（Ⅰ）由同角三角函数基本关系式可求sin∠ADB，由．利用两角差的正弦函数公式及特殊角的三角函数值即可求值得解．（Ⅱ）先由正弦定理求AD的值，再利用三角形面积公式即可得解．【解答】（本小题满分13分）解：（Ⅰ）因为，所以．又因为，所以．所以=．…（Ⅱ）在△ACD中，由，得．所以．…17．如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠DAB=60°．点E是棱PC的中点，平面ABE与棱PD交于点F．（Ⅰ）求证：AB∥EF；（Ⅱ）若PA=PD=AD，且平面PAD⊥平面ABCD，求平面PAF与平面AFE所成的锐二面角的余弦值．【考点】二面角的平面角及求法；空间中直线与直线之间的位置关系．【分析】（Ⅰ）推导出AB∥CD，从而AB∥面PCD，由此能证明AB∥EF．（Ⅱ）取AD中点G，连接PG，GB．以G为原点，GA为x轴，GB为y轴，GP为z轴，建立空间直角坐标系G﹣xyz．利用向量法能求出平面PAF与平面AFE所成的锐二面角的余弦值．【解答】（本小题满分13分）证明：（Ⅰ）因为底面ABCD是菱形，所以AB∥CD．又因为AB⊄面PCD，CD⊂面PCD，所以AB∥面PCD．又因为A，B，E，F四点共面，且平面ABEF∩平面PCD=EF，所以AB∥EF．…解：（Ⅱ）取AD中点G，连接PG，GB．因为PA=PD，所以PG⊥AD．又因为平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，所以PG⊥平面ABCD．所以PG⊥GB．在菱形ABCD中，因为AB=AD，∠DAB=60°，G是AD中点，所以AD⊥GB．如图，以G为原点，GA为x轴，GB为y轴，GP为z轴，建立空间直角坐标系G﹣xyz．设PA=PD=AD=2a，则G（0，0，0），A（a，0，0），．又因为AB∥EF，点E是棱PC中点，所以点F是棱PD中点．所以，．所以，．设平面AFE的法向量为n=（x，y，z），则有所以令x=3，则平面AFE的一个法向量为．因为BG⊥平面PAD，所以是平面PAF的一个法向量．因为，所以平面PAF与平面AFE所成的锐二面角的余弦值为．…18．已知函数f（x）=ax+lnx，其中a∈R．（Ⅰ）若f（x）在区间上为增函数，求a的取值范围；（Ⅱ）当a=﹣e时，（ⅰ）证明：f（x）+2≤0；（ⅱ）试判断方程是否有实数解，并说明理由．【考点】利用导数研究函数的单调性；利用导数求闭区间上函数的最值．【分析】（Ⅰ）求出函数的导数，分离出a，结合函数的单调性求出a的范围即可；（Ⅱ）（i）解关于导函数的不等式，求出函数的单调区间，从而求出f（x）的最大值，证出结论；（ii）求出|f（x）|≥2，令g（x）=+，求出g（x）的最大值小于|f（x）|的最小值，从而判断无解．【解答】解：函数f（x）定义域x∈（0，+∞），f′（x）=a+，（Ⅰ）因为f（x）在区间上为增函数，所以f′（x）≥0在x∈上恒成立，即，在x∈上恒成立，则．…（Ⅱ）当a=﹣e时，f（x）=﹣ex+lnx，．（ⅰ）令f′（x）=0，得．令f′（x）＞0，得，所以函数f（x）在单调递增．令f′（x）＜0，得，所以函数f（x）在单调递减．所以，．所以f（x）+2≤0成立．…（ⅱ）由（ⅰ）知，f（x）max=﹣2，所以|f（x）|≥2．设．所以．令g'（x）=0，得x=e．令g'（x）＞0，得x∈（0，e），所以函数g（x）在（0，e）单调递增，令g'（x）＜0，得x∈（e，+∞），所以函数g（x）在（e，+∞）单调递减；所以，，即g（x）＜2．所以|f（x）|＞g（x），即|f（x）|＞．所以，方程|f（x）|=没有实数解．…19．已知圆O：x2+y2=1的切线l与椭圆C：x2+3y2=4相交于A，B两点．（Ⅰ）求椭圆C的离心率；（Ⅱ）求证：OA⊥OB；（Ⅲ）求△OAB面积的最大值．【考点】椭圆的简单性质．【分析】（Ⅰ）由题意可得椭圆的a，b，c，由离心率公式可得所求值；（Ⅱ）讨论切线的斜率不存在和存在，设出直线方程，联立椭圆方程，运用韦达定理和向量的数量积的坐标表示，化简整理，即可得证；（Ⅲ）因为直线AB与圆O相切，则圆O半径即为△OAB的高．讨论当l的斜率不存在时，由（Ⅱ）可知|AB|=2．则S△OAB=1．当l的斜率存在时，运用弦长公式和点到直线的距离公式，运用基本不等式可得面积的最大值．【解答】解：（Ⅰ）由题意可知a2=4，，即有．则．故椭圆C的离心率为；（Ⅱ）证明：若切线l的斜率不存在，则l：x=±1．在中，令x=1得y=±1．不妨设A（1，1），B（1，﹣1），则．可得OA⊥OB；同理，当l：x=﹣1时，也有OA⊥OB．若切线l的斜率存在，设l：y=kx+m，依题意，即k2+1=m2．由，得（3k2+1）x2+6kmx+3m2﹣4=0．显然△＞0．设A（x1，y1），B（x2，y2），则，．所以．所以=====．所以OA⊥OB．综上所述，总有OA⊥OB成立．（Ⅲ）因为直线AB与圆O相切，则圆O半径即为△OAB的高．当l的斜率不存在时，由（Ⅱ）可知|AB|=2．则S△OAB=1．当l的斜率存在时，由（Ⅱ）可知，====．所以=，（当且仅当时，等号成立）．所以．此时，．综上所述，当且仅当时，△OAB面积的最大值为．20．已知有穷数列：的各项均为正数，且满足条件：①a1=a k；②．（Ⅰ）若k=3，a1=2，求出这个数列；（Ⅱ）若k=4，求a1的所有取值的集合；（Ⅲ）若k是偶数，求a1的最大值（用k表示）．【考点】数列的应用．【分析】（Ⅰ）∵k=3，a1=2，由①知a3=2；由②知，，整理得，a2．即可得出a3．（II）若k=4，由①知a4=a1．由于，解得或．分类讨论即可得出．（Ⅲ）依题意，设k=2m，m∈N*，m≥2．由（ II）知，或．假设从a1到a2m恰用了i次递推关系，用了2m﹣1﹣i次递推关系，则有，其中|t|≤2m ﹣1﹣i，t∈Z．对i分类讨论即可得出．【解答】解：（Ⅰ）∵k=3，a1=2，由①知a3=2；由②知，，整理得，．解得，a2=1或．当a2=1时，不满足，舍去；∴这个数列为．（Ⅱ）若k=4，由①知a4=a1．∵，∴．∴或．如果由a1计算a4没有用到或者恰用了2次，显然不满足条件；∴由a1计算a4只能恰好1次或者3次用到，共有下面4种情况：（1）若，，，则，解得；（2）若，，，则，解得a1=1；（3）若，，，则，解得a1=2；（4）若，，，则，解得a1=1；综上，a1的所有取值的集合为．（Ⅲ）依题意，设k=2m，m∈N*，m≥2．由（ II）知，或．假设从a1到a2m恰用了i次递推关系，用了2m﹣1﹣i次递推关系，则有，其中|t|≤2m﹣1﹣i，t∈Z．当i是偶数时，t≠0，无正数解，不满足条件；当i是奇数时，由得，∴．又当i=1时，若，有，，即．∴a1的最大值是2m﹣1．即．2016年8月22日。