2010一模参考(海淀)

2010年北京市中考模拟试卷汇总：圆2010年北京市中考模拟试卷汇总：圆一、选择题（共1小题，每小题4分，满分4分）1．（4分）（2011•通州区一模）如图，⊙O的半径为2，直线PA、PB为⊙O的切线，A、B为切点，若PA⊥PB，则OP的长为（）．D二、填空题（共2小题，每小题5分，满分10分）2．（5分）（2004•乌当区一模）如图：AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10cm，CD=8cm，那么AE的长为_________cm．3．（5分）（2009•贺州）如图，正方形ABCD是⊙O的内接正方形，点P是劣弧上不同于点B的任意一点，则∠BPC=_________度．三、解答题（共35小题，满分0分）4．（2010•朝阳区一模）如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，DB=6cm．（1）求证：AC是⊙O的切线；（2）求⊙O的半径长；（3）求由弦CD、BD与弧BC所围成的阴影部分的面积（结果保留π）．5．（2013•泰兴市模拟）如图，AB是半圆O的直径，过点O作弦AD的垂线交半圆O于点E，交AC于点C，使∠BED=∠C．（1）判断直线AC与圆O的位置关系，并证明你的结论；（2）若AC=8，，求AD的长．6．（2009•大连）如图，在⊙O中，AB是直径，AD是弦，∠ADE=60°，∠C=30度．（1）判断直线CD是否是⊙O的切线，并说明理由；（2）若CD=，求BC的长．7．（2012•朝阳一模）已知：如图，AB为⊙O的直径，⊙O过AC的中点D，DE⊥BC于点E．（1）求证：DE为⊙O的切线；（2）若DE=2，tanC=，求⊙O的直径．8．（2011•玉溪一模）已知：如图，⊙O为△ABC的外接圆，BC为⊙O的直径，作射线BF，使得BA平分∠CBF，过点A作AD⊥BF于点D．（1）求证：DA为⊙O的切线；（2）若BD=1，，求⊙O的半径．9．（2010•石景山区一模）已知：如图，AB为⊙O的直径，弦AC∥OD，BD切⊙O于B，连接CD．（1）判断CD是否为⊙O的切线，若是请证明；若不是请说明理由；（2）若AC=2，OD=6，求⊙O的半径．10．（2012•姜堰市二模）如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A，AD与BC交于点E，F在DA的延长线上，且AF=AE．（1）求证：BF是⊙O的切线；（2）若AD=4，，求BC的长．11．（2010•宣武区一模）已知：如图，⊙O是△ABC的外接圆，AB为⊙O直径，且PA⊥AB于点A，PO⊥AC于点M （1）求证：PC是⊙O的切线；（2）当，时，求PC的长．12．（2009•鄂尔多斯）如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．（1）求证：DE是⊙O的切线；（2）若∠C=30°，CE=5，求⊙O的半径．13．已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且OA=AB=AD．（1）求证：BD是⊙O的切线；（2）若点E是劣弧BC上一点，AE与BC相交于点F，且BE=8，tan∠BFA=，求⊙O的半径长．14．（2010•房山区一模）已知：如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O 是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．（1）求证：AC与⊙O相切；（2）当BD=2，sinC=时，求⊙O的半径．15．（2011•无锡一模）如图，已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于B．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为3，AB=4，求AD的长．16．（2010•门头沟区一模）已知：如图，BE是⊙O的直径，CB与⊙O相切于点B，OC∥DE交⊙O于点D，CD的延长线与BE的延长线交于A点．（1）求证：AC是⊙O的切线；（2）若AD=4，CD=6，求tan∠ADE的值．17．（2010•密云县）如图，等腰三角形ABC中，AC=BC=10，AB=12．以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．（1）求证：直线EF是⊙O的切线；（2）求sin∠E的值．18．（2010•顺义区）如图，⊙O的直径AB=4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．（1）求证：EF是⊙O的切线；（2）求DE的长．19．（2010•通州区一模）如图，平行四边形ABCD中，以A为圆心，AB为半径的圆交AD于F，交BC于G，延长BA交圆于E．（1）若ED与⊙A相切，试判断GD与⊙A的位置关系，并证明你的结论；（2）在（1）的条件不变的情况下，若GC=CD=5，求AD的长．20．（2013•滨湖区一模）如图，AB为⊙O的直径，AD平分∠BAC交⊙O于点D，DE⊥AC交AC的延长线于点E，BF⊥AB交AD的延长线于点F，（1）求证：DE是⊙O的切线；（2）若DE=3，⊙O的半径为5，求BF的长．21．如图，AB是⊙O的直径，点C在⊙O上，M是的中点，OM交⊙O的切线BP于点P．（1）判断直线PC和⊙O的位置关系，并证明你的结论；（2）若sin∠BAC=0.8，⊙O的半径为2，求线段PC的长．22．（2013•兰州）已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN 于E．（1）求证：DE是⊙O的切线；（2）若DE=6cm，AE=3cm，求⊙O的半径．23．（2011•房山区一模）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC、AC于点D、E，连接EB交OD于点F．（1）求证：OD⊥BE；（2）若DE=，AB=，求AE的长．24．（2010•顺义区二模）如图，AB是⊙O的直径，BD交⊙O于点C，AE平分∠BAC，EF⊥AB，垂足为F，∠D=∠CAB．（1）求证：AD为⊙O的切线；（2）若，AD=6，求CE的长．25．已知：如图，AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．（1）求证：AD⊥DC；（2）若AD=2，tan∠DAC=，求⊙O直径AB的长．26．（2008•泰安）如图所示，△ABC是直角三角形，∠ABC=90°，以AB为直径的⊙O交AC于点E，点D是BC边的中点，连接DE．（1）求证：DE与⊙O相切；（2）若⊙O的半径为，DE=3，求AE．27．（2010•房山区二模）如图，以Rt△ABC的一直角边AB为直径作圆，交斜边BC于P点，Q为AC的中点．28．（2010•朝阳区二模）已知：如图，AB=AC，AB是⊙O的直径，与BC交于点D，延长CA交⊙O于点F，连接DF，DE⊥CF于点E．（1）求证：DE是⊙O的切线；（2）若AB=10，cosC=，求EF的长．29．（2009•陕西）如图，圆O是△ABC的外接圆，AB=AC，过点A作AP∥BC，交BO的延长线于点P．（1）求证：AP是圆O的切线；（2）若圆O的半径R=5，BC=8，求线段AP的长．30．（2010•丰台区二模）已知：如图，AB是半圆O的直径，OD是半径，BM切半圆于点B，OC与弦AD平行交BM于点C．（1）求证：CD是半圆O的切线；（2）若AB的长为4，点D在半圆O上运动，当AD的长为1时，求点A到直线CD的距离．31．（2010•延庆县二模）如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，连接CD且DC=BC，过C 点作AD的垂线交AD延长线于E，32．（2009•梧州）如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，过点C的切线交AD的延长线于点E，且AE⊥CE，连接CD．（1）求证：DC=BC；（2）若AB=5，AC=4，求tan∠DCE的值．33．（2010•门头沟区二模）已知：如图，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC=∠ODB．（1）求证：BD是⊙O的切线；（2）当AB=10，BC=8时，求BD的长．34．（2010•石景山区二模）已知：如图，AB=BC，以AB为直径的⊙O交AC于点D，DE是⊙O的切线，过点D作DG⊥AB交圆于点G，（1）求证：DE⊥BC；（2）若tan∠C=，BE=2，求弦DG的长．35．（2009•德州）如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线l，过点B作l的垂线BD，36．（2012•清远一模）已知：如图，△ABC内接于⊙O，点D在OC的延长线上，sinB=，∠CAD=30°．（1）求证：AD是⊙O的切线；（2）若OD⊥AB，BC=5，求AD的长．37．（2010•海淀区二模）已知：如图，点C在以AB为直径的⊙O上，点D在AB的延长线上，∠BCD=∠A．（1）求证：CD为⊙O的切线；（2）过点C作CE⊥AB于E，若，求⊙O的半径．38．（2010•东城区二模）将一个量角器和一个含30°角的直角三角板如图1放置，图2是由它抽象出的几何图形，其中点B在半圆O的直径DE的延长线上，AB切半圆O于点F，BC=OD（1）求证：FC∥DB；（2）当OD=3，sin∠ABD=时，求AF的长．2010年北京市中考模拟试卷汇总：圆参考答案与试题解析一、选择题（共1小题，每小题4分，满分4分）1．（4分）（2011•通州区一模）如图，⊙O的半径为2，直线PA、PB为⊙O的切线，A、B为切点，若PA⊥PB，则OP的长为（）．DBPO=OP===2二、填空题（共2小题，每小题5分，满分10分）2．（5分）（2004•乌当区一模）如图：AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10cm，CD=8cm，那么AE的长为8cm．=3cm3．（5分）（2009•贺州）如图，正方形ABCD是⊙O的内接正方形，点P是劣弧上不同于点B的任意一点，则∠BPC= 45度．∠三、解答题（共35小题，满分0分）4．（2010•朝阳区一模）如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，DB=6cm．（1）求证：AC是⊙O的切线；（2）求⊙O的半径长；（3）求由弦CD、BD与弧BC所围成的阴影部分的面积（结果保留π）．DE=BE=，∴∴5．（2013•泰兴市模拟）如图，AB是半圆O的直径，过点O作弦AD的垂线交半圆O于点E，交AC于点C，使∠BED=∠C．（1）判断直线AC与圆O的位置关系，并证明你的结论；（2）若AC=8，，求AD的长．BED=，利用BED=，BED=，×．6．（2009•大连）如图，在⊙O中，AB是直径，AD是弦，∠ADE=60°，∠C=30度．（1）判断直线CD是否是⊙O的切线，并说明理由；（2）若CD=，求BC的长．tanC=tanC=3×=37．（2012•朝阳一模）已知：如图，AB为⊙O的直径，⊙O过AC的中点D，DE⊥BC于点E．（1）求证：DE为⊙O的切线；（2）若DE=2，tanC=，求⊙O的直径．，可求，，可求tanC=EC=DC=，8．（2011•玉溪一模）已知：如图，⊙O为△ABC的外接圆，BC为⊙O的直径，作射线BF，使得BA平分∠CBF，过点A作AD⊥BF于点D．（1）求证：DA为⊙O的切线；（2）若BD=1，，求⊙O的半径．，AB==DBA=BC==59．（2010•石景山区一模）已知：如图，AB为⊙O的直径，弦AC∥OD，BD切⊙O于B，连接CD．（1）判断CD是否为⊙O的切线，若是请证明；若不是请说明理由；（2）若AC=2，OD=6，求⊙O的半径．∴AC=1∴±的半径为10．（2012•姜堰市二模）如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A，AD与BC交于点E，F在DA的延长线上，且AF=AE．（1）求证：BF是⊙O的切线；（2）若AD=4，，求BC的长．根据∴∴，∴∴11．（2010•宣武区一模）已知：如图，⊙O是△ABC的外接圆，AB为⊙O直径，且PA⊥AB于点A，PO⊥AC于点M （1）求证：PC是⊙O的切线；（2）当，时，求PC的长．BC=2，∴，PC=4．12．（2009•鄂尔多斯）如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．（1）求证：DE是⊙O的切线；（2）若∠C=30°，CE=5，求⊙O的半径．C=B=，的半径为C=B==OB=的半径为13．已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且OA=AB=AD．（1）求证：BD是⊙O的切线；（2）若点E是劣弧BC上一点，AE与BC相交于点F，且BE=8，tan∠BFA=，求⊙O的半径长．，得到=，求出直径∠BFA=aBFA===∴=，的值，然后利用相似三角形求出直径的长，再确定圆的半径的长．14．（2010•房山区一模）已知：如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O 是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．（1）求证：AC与⊙O相切；（2）当BD=2，sinC=时，求⊙O的半径．sinC=sinA=sinC=．sinA==r=．15．（2011•无锡一模）如图，已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于B．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为3，AB=4，求AD的长．∴∴∴16．（2010•门头沟区一模）已知：如图，BE是⊙O的直径，CB与⊙O相切于点B，OC∥DE交⊙O于点D，CD的延长线与BE的延长线交于A点．（1）求证：AC是⊙O的切线；（2）若AD=4，CD=6，求tan∠ADE的值．∴OCB=17．（2010•密云县）如图，等腰三角形ABC中，AC=BC=10，AB=12．以BC为直径作⊙O交AB于点D，交AC 于点G，DF⊥AC，垂足为F，交CB的延长线于点E．（1）求证：直线EF是⊙O的切线；（2）求sin∠E的值．CD= BG= CG=CBG=．18．（2010•顺义区）如图，⊙O的直径AB=4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．（1）求证：EF是⊙O的切线；（2）求DE的长．19．（2010•通州区一模）如图，平行四边形ABCD中，以A为圆心，AB为半径的圆交AD于F，交BC于G，延长BA交圆于E．（1）若ED与⊙A相切，试判断GD与⊙A的位置关系，并证明你的结论；（2）在（1）的条件不变的情况下，若GC=CD=5，求AD的长．∠20．（2013•滨湖区一模）如图，AB为⊙O的直径，AD平分∠BAC交⊙O于点D，DE⊥AC交AC的延长线于点E，BF⊥AB交AD的延长线于点F，（1）求证：DE是⊙O的切线；（2）若DE=3，⊙O的半径为5，求BF的长．=，即可求出∴，即，．21．如图，AB是⊙O的直径，点C在⊙O上，M是的中点，OM交⊙O的切线BP于点P．（1）判断直线PC和⊙O的位置关系，并证明你的结论；（2）若sin∠BAC=0.8，⊙O的半径为2，求线段PC的长．BAC=，；．22．（2013•兰州）已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN 于E．（1）求证：DE是⊙O的切线；（2）若DE=6cm，AE=3cm，求⊙O的半径．∴∴∴23．（2011•房山区一模）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC、AC于点D、E，连接EB交OD于点F．（1）求证：OD⊥BE；（2）若DE=，AB=，求AE的长．BD=ED=OF=，中，中，∴，即．24．（2010•顺义区二模）如图，AB是⊙O的直径，BD交⊙O于点C，AE平分∠BAC，EF⊥AB，垂足为F，∠D=∠CAB．（1）求证：AD为⊙O的切线；（2）若，AD=6，求CE的长．）解：∵CAB=×，∴××=2.425．已知：如图，AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．（1）求证：AD⊥DC；（2）若AD=2，tan∠DAC=，求⊙O直径AB的长．AC=∵DAC=，DC=AD=×．连接∴．．的长是26．（2008•泰安）如图所示，△ABC是直角三角形，∠ABC=90°，以AB为直径的⊙O交AC于点E，点D是BC边的中点，连接DE．（1）求证：DE与⊙O相切；（2）若⊙O的半径为，DE=3，求AE．，AC=4AE=：∵（∴∴．27．（2010•房山区二模）如图，以Rt△ABC的一直角边AB为直径作圆，交斜边BC于P点，Q为AC的中点．（1）求证：PQ与⊙O相切；（2）若PQ=2cm，BP=6cm，求圆的半径．∴AB=所求圆的半径为28．（2010•朝阳区二模）已知：如图，AB=AC，AB是⊙O的直径，与BC交于点D，延长CA交⊙O于点F，连接DF，DE⊥CF于点E．（1）求证：DE是⊙O的切线；（2）若AB=10，cosC=，求EF的长．cosC=cosB=cosF=cosB=DE=cosF=cosB=x=EF=，29．（2009•陕西）如图，圆O是△ABC的外接圆，AB=AC，过点A作AP∥BC，交BO的延长线于点P．（1）求证：AP是圆O的切线；（2）若圆O的半径R=5，BC=8，求线段AP的长．BE=∴∴∴30．（2010•丰台区二模）已知：如图，AB是半圆O的直径，OD是半径，BM切半圆于点B，OC与弦AD平行交BM于点C．（1）求证：CD是半圆O的切线；（2）若AB的长为4，点D在半圆O上运动，当AD的长为1时，求点A到直线CD的距离．AE=的距离为．31．（2010•延庆县二模）如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，连接CD且DC=BC，过C 点作AD的垂线交AD延长线于E，（1）求证：CE是⊙O的切线；（2）若AB=5，AC=4，求tan∠DCE的值．∴，=．32．（2009•梧州）如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，过点C的切线交AD的延长线于点E，且AE⊥CE，连接CD．（1）求证：DC=BC；（2）若AB=5，AC=4，求tan∠DCE的值．，进而证明∴BC=∴∴∴DCE=．33．（2010•门头沟区二模）已知：如图，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC=∠ODB．（1）求证：BD是⊙O的切线；（2）当AB=10，BC=8时，求BD的长．∴．34．（2010•石景山区二模）已知：如图，AB=BC，以AB为直径的⊙O交AC于点D，DE是⊙O的切线，过点D作DG⊥AB交圆于点G，（1）求证：DE⊥BC；（2）若tan∠C=，BE=2，求弦DG的长．DG=2DF=35．（2009•德州）如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点E．求证：四边形OBEC是菱形．36．（2012•清远一模）已知：如图，△ABC内接于⊙O，点D在OC的延长线上，sinB=，∠CAD=30°．（1）求证：AD是⊙O的切线；（2）若OD⊥AB，BC=5，求AD的长．，那么可求∠，AC=AD=2AE=537．（2010•海淀区二模）已知：如图，点C在以AB为直径的⊙O上，点D在AB的延长线上，∠BCD=∠A．（1）求证：CD为⊙O的切线；。

北京海淀区一模考试已结束，新东方在线、北京新东方优能中学高考辅导团队第一时间各科题目进行了解析，希望能对全国考生的备考有所帮助。

以下是高考英语教研组的老师们对英语题目的点评及解析。

听力理解部分总体而言，2013海淀一模听力部分总体来说难度低于北京卷高考水平，没有太多混淆的题目和含糊的表达，而它真正的难度在于本次考试发音属英音，考生听起来可能有些不适应。

如果按照平时学习和练习水平发挥，应该不会有太大问题。

若感觉本次考试有难度，考生需加强听力练习，并多听英音磨耳朵。

历届北京市高考听力真题就是不错的练习材料，可以反复听音并做复述或听写训练。

考题当中的考点也都如新东方高考教研组内解析、预测一样，没有出入。

如，第一部分短对话当中，虽然1，3，5题的选项和对话内容有多个重合，但是提前审题、预判答案会有很大帮助；第二节中的对话和独白也需要考生集中精力，看准问题再有针对性的分析，解题正确率就会很高；第三节的听写填空中，也如新东方组内解析《2013高考大纲》所预测出的一样，会考查大小写、国家/语言的专有名词、数字等，只是本次考试难度偏低，第26题数字填空部分没有在发音、长度或字母数字混合上难为考生，仅仅出了一个两位数“29”。

若按照课上老师明确提示准备考试，一定会取得好成绩。

在此将所有题目按照《2013考试大纲》中的英语“听”的部分考查技能分类，并选部分题目讲解： 1、理解归纳话语的主旨要义 对应考题：3 主旨要义类题目提问方式常带有“mainly talking about”这样的表达，此类题目偏难，往往所有选项表达均与对话内容重合。

此时考生需要寻找对话中心，找准引发其他选项的活动或名词。

特别注意的是，此类题目往往对话一开始就直指主题，一定要集中精力。

如本题springbreak即为对话中心，潜水和酒店都是由此引发的，对话内容也是在开始，女士问“Jim, have you got any ideas for our spring break?”本题需要提醒考生注意break本题中为“休息”；另外，scuba diving意为“重装潜水” 2、获取事实信息 对应考题：1、5、7、10、11、13、14、15这类题目考查最多，但难度不是很大。

海淀区高三年级第二学期期中练习理科综合能力测试13．下列说法中正确的是A ．机械波和电磁波都能发生反射、折射、干涉和衍射现象，这是因为它们都可以在真空中传播B ．变化的电场一定产生变化的磁场，变化的磁场一定产生变化的电场C ．站在地面上的人观察一根相对地面沿杆长方向高速运动的杆，他发现杆的长度比静止时的长度小D ．狭义相对论的两个假设之一是真空中的光速在不同惯性参考系中是不相同的 14．如图所示为氢原子的能级图，用大量能量为12.76eV 的光子照射一群处于基态的氢原子，氢原子发射出不同波长的光波，其中最多包含有几种不同波长的光波？ A ．3种 B ．4种 C ．5种 D ．6种15．如图所示，一束复色光斜射到置于空气中的厚平板玻璃（上、下表面平行）的上表面，复色光穿穿过玻璃后从下表面射出，变为a 、b 两束平行单色光。

关于这两束单色光，下列说法中正确的是 A ．此玻璃对a 光的折射率小于对b 光的折射率B ．在此玻璃中a 光的全反射临界角小于b 光的全反射临界角C ．在此玻璃中a 光的传播速度大于b 光的传播速度D ．用同一双缝干涉装置进行实验，可看到a 光的干涉条纹间距比b 光的宽 16．在研究宇宙发展演变的理论中，有一种学说叫做“宇宙膨胀说”，这种学说认为引力常量G 在缓慢地减小。

假设月球绕地球做匀速圆周运动，且它们的质量始终保持不变，根据这种学说当前月球绕地球做匀速圆周运动的情况与很久很久以前相比A ．周期变大B ．角速度变大C ．轨道半径减小D ．速度变大 17．如图甲是某小型家用电器电源部分的主要工作电路图，工作时Ⅰ部分变压器原线圈A 、B 两端与输出电压为220V 的交流电源相连接，通过电路元件的工作最后在Ⅲ部分E 、F 两端输出6.0V 的直流电。

当A 、B 两端输入如图5乙所示的交变电压时，在Ⅱ部分的M 、N 两端输出的电压如图5丙所示。

Ⅲ部分中的自感线圈L 的直流电阻可忽略不计，关于该电路元件及其工作过程，下列说法中正确的是A ．Ⅰ部分的变压器是降压变压器B ．Ⅲ部分的自感线圈L 的作用是阻碍直流成分，导通交流成分C ．Ⅲ部分的电容器C 的作用是阻碍交流成分，导通直流成分D ． M 、N 两端输出电压的有效值为2U 01-13.612 -3.403-1.51 4 -0.855 -0.54 ∞0 n E /eV U i -U U 乙 丙18．如图所示，将一个筛子用四根弹簧支起来（后排的两根弹簧未画出），筛子上装一个电动偏心轮，这就做成了一个共振筛。

海淀一模第 25 题所考知识点及试题分析 一、试题介绍： 5 月 12 日，海淀区初中一模考试数学试卷已经发布出来了，看了一下第 25 题，经过细致分析，发现这次 试题相比去年的一模试题难度没有变化，考察的知识点仍然比较全面，涉及到的方法仍然灵活多变。

下面 做一个简要分析。

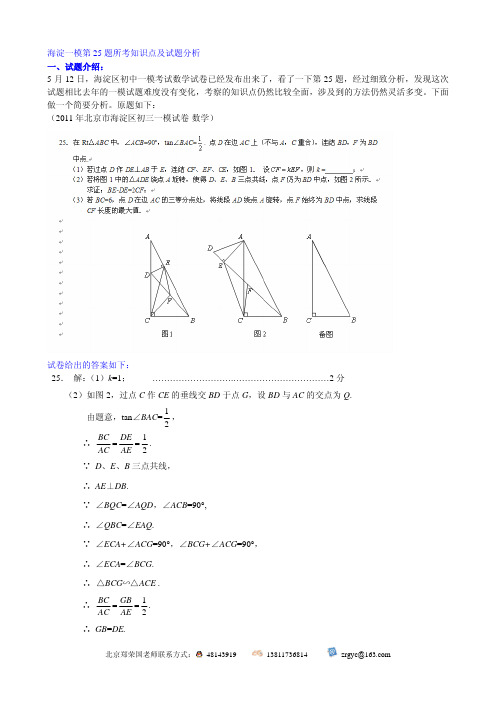
原题如下： （2011 年北京市海淀区初三一模试卷-数学）试卷给出的答案如下： 25． 解： （1）k=1；……………………….……………………………2 分（2）如图 2，过点 C 作 CE 的垂线交 BD 于点 G，设 BD 与 AC 的交点为 Q. 由题意，tan∠BAC= ∴1 ， 2BC DE 1 = = . AC AE 2∵ D、E、B 三点共线， ∴ AE⊥DB. ∵ ∠BQC=∠AQD，∠ACB=90°, ∴ ∠QBC=∠EAQ. ∵ ∠ECA+∠ACG=90°，∠BCG+∠ACG=90°， ∴ ∠ECA=∠BCG. ∴ △BCG∽△ ACE .∴BC GB 1 = = . AC AE 2∴ GB=DE.北京郑荣国老师联系方式： 48143919 138******** zrgyc@∵ F 是 BD 中点， ∴ F 是 EG 中点. 在 Rt△ECG 中， CF = 1 EG , 2∴ BE − DE = EG = 2CF . .…………………………….……………………………5 分 1 （3）情况 1：如图，当 AD= AC 时，取 AB 的中点 M，连结 MF 和 CM， 3 ∵∠ACB=90°， tan∠BAC= ∴AC=12，AB= 6 5 . ∵M 为 AB 中点，∴CM= 3 5 , 1 ，且 BC= 6, 21 ∵AD= AC ， 3∴AD= 4 . ∵M 为 AB 中点，F 为 BD 中点， ∴FM=1 AD = 2. 2∴当且仅当 M、F、C 三点共线且 M 在线段 CF 上时 CF 最大，此时 CF=CM+FM= 2 + 3 5 ..…………………………….……………………………6 分A D EDA DAQFFM FMG CB图2情况 2：如图，当 AD=CBCB2 AC 时，取 AB 的中点 M， 3连结 MF 和 CM， 类似于情况 1，可知 CF 的最大值为 4 + 3 5 . ……………………………7 分 综合情况 1 与情况 2，可知当点 D 在靠近点 C 的三等分点时，线段 CF 的长度取得最大值为4 + 3 5 ………………………8 分本题涉及的知识点主要有：两点之间线段最短、线段的中点、直角三角形的性质、中心对称、旋转变换、 图形的全等与相似、三角形的中位线、动态分析 ．．．．北京郑荣国老师联系方式： 48143919 138******** zrgyc@本题涉及到的思想方法主要有：转化的思想、化归思想 二、再探解题思路和方法： 先通读全题，得到△ABC 和△ADE 是相似三角形，并且二者均为特殊三角形（三边之比为 1:2： 5 ） 。

2010年北京中考数学模拟分类 二次函数综合题1.（2010北京中考）24. 在平面直角坐标系xOy 中，拋物线y = -41-m x 2+45mx +m 2-3m +2 与x 轴的交点分别为原点O 和点A ，点B (2，n )在这条拋物线上。

(1) 求点B 的坐标；(2) 点P 在线段OA 上，从O 点出发向点运动，过P 点作x 轴的垂线，与直线OB 交于点E 。

延长PE 到点D 。

使得ED =PE 。

以PD 为斜边在PD 右侧作等腰直角三角形PCD (当P 点运动时，C 点、D 点也随之运动) 当等腰直角三角形PCD 的顶点C 落在此拋物线上时，求OP 的长；若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位(当Q 点到达O 点时停止 运动，P 点也同时停止运动)。

过Q 点作x 轴的垂线，与直线AB 交于点F 。

延长QF 到点M ，使得FM =QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN (当Q 点运动时，M 点，N 点也随之运动)。

若P 点运动到t 秒时，两个等腰直角三角形分别有一条直角边恰好落在同一条直线上，求此刻t 的值。

2.( 2010朝阳一模24)已知直线y=kx-3与x 轴交于点A （4，0），与y 轴交于点C ，抛物线234y x mx n =-++经过点A 和点C,动点P 在x 轴上以每秒1个长度单位的速度由抛物线与x 轴的另一个交点B 向点A 运动，点Q 由点C 沿线段CA 向点A 运动且速度是点P 运动速度的2倍. （1）求此抛物线的解析式和直线的解析式； （2）如果点P 和点Q 同时出发，运动时间为t （秒），试问当t 为何值时，△PQA 是直角三角形；（3）在直线CA 上方的抛物线上是否存在一点D ，使得△ACD 的面积最大，若存在，求出点D 坐标；若不存在，请说明理由．3.( 2010东城一模) 23. 已知抛物线C 1：22y x x =-的图象如图所示，把C 1的图象沿y 轴翻折，得到抛物线C 2的图象，抛物线C 1与抛物线C 2的图象合称图象C 3（1）求抛物线C 1的顶点A 坐标，并画出抛物线C 2的图象； （2）若直线y kx b =+与抛物线2(0)y ax bx c a =++≠点时,称直线与抛物线相切. 若直线y x b =+与抛物线C 1相切，求b 的值；（3）结合图象回答，当直线y x b =+与图象C 3 有两个交点时，b 值范围．4. （2010丰台一模）23．已知二次函数22-+-=m mx x y ．（1） 求证：无论m 为任何实数，该二次函数的图象与x 轴都有两个交点； （2） 当该二次函数的图象经过点（3，6）时，求二次函数的解析式；（3） 将直线y =x 向下平移2个单位长度后与（2）中的抛物线交于A 、B 两点（点A 在点B 的左边），一个动点P 自A 点出发，先到达抛物线的对称轴上的某点E ，再到达x 轴上的某点F ，最后运动到点B ．求使点P 运动的总路径最短的点E 、点F 的坐标，并求出这个最短总路径的长．5. （2010丰台一模）25．已知抛物线22--=x x y ．（1）求抛物线顶点M 的坐标；（2）若抛物线与x 轴的交点分别为点A 、B （点A 在点B 的左边），与y 轴交于点C ，点N 为线段BM 上的一点，过点N 作x 轴的垂线，垂足为点Q ．当点N 在线段BM 上运动时（点N 不与点B ，点M 重合），设NQ 的长为t ，四边形NQAC 的面积为S ，求S 与t 之间的函数关系式及自变量t 的取值范围； （3）在对称轴右侧的抛物线上是否存在点P ，使△P AC 为直角三角形?若存在，求出所有符合条件的点P 的坐标；若不存在，请说明理由．6.（2010海淀一模） 24. 点P 为抛物线222y x mx m =-+(m 为常数，0m >)上任一点，将抛物线绕顶点G 逆时针旋转90︒后得到的新图象与y 轴交于A 、B 两点(点A 在点B 的上方)，点Q 为点P 旋转后的对应点.(1) 当2m =，点P 横坐标为4时，求Q 点的坐标； (2) 设点(,)Q a b ，用含m 、b 的代数式表示a ；(3) 如图，点Q 在第一象限内, 点D 在x 轴的正半轴上，点C 为OD 的中点，QO 平分AQC ∠，2AQ QC =，当QD m =时，求m 的值.7.（2010海淀一模）23.关于x 的一元二次方程240x x c -+=有实数根，且c 为正整数.(1) 求c 的值；(2) 若此方程的两根均为整数，在平面直角坐标系xOy 中,抛物线24y x x c =-+与x 轴交于A 、B 两点(A 在B 左侧)，与y 轴交于点C . 点P 为对称轴上一点，且四边形OBPC 为直角梯形，求PC 的长； (3) 将(2)中得到的抛物线沿水平方向平移，设顶点D 的坐标为(),m n ,当抛物线与(2)中的直角梯形OBPC 只有两个交点，且一个交点在PC 边上时，直接写出m 的取值范围.8. （2010石景山一模）25．已知：如图1，等边ABC ∆的边长为32，一边在x 轴上且()0,31-A ，AC 交y 轴于点E ，过点E 作EF ∥AB 交BC 于点F ．（1）直接写出点C B 、的坐标；（2）若直线()01≠-=k kx y 将四边形EABF 的面积两等分，求k 的值；（3）如图2，过点C B A 、、的抛物线与y 轴交于点D ，M 为线段OB 上的一个动点，过x 轴上一点()0,2-G 作DM 的垂线，垂足为H ，直线GH 交y 轴于点N ，当M 点在线段OB 上运动时，现给出两个结论：① CDM GNM ∠=∠ ②DCM MGN ∠=∠，其中有且只有一个结论是正确的，请你判断哪个结论正确，并证明．图1 图29.（2010西城一模） 23．已知关于x 的方程032)1(32=-+--m x m mx ．（1）求证：无论m 取任何实数时，方程总有实数根；（2）若关于x 的二次函数32)1(321-+--=m x m mx y 的图象关于y 轴对称． ①求这个二次函数的解析式；②已知一次函数222-=x y ，证明：在实数范围内，对于x 的同一个值，这两个函数所对应的函数值y 1≥y 2均成立；（3）在（2）的条件下，若二次函数y 3＝ax 2＋bx ＋c 的图象经过点（－5，0），且在实数范围内，对于x 的同一个值，这三个函数所对应的函数值y 1≥y 3≥y 2均成立．求二次函数y 3＝ax 2＋bx ＋c 的解析式.10.（2010宣武一模）24．已知：将函数y x =的图象向上平移2个单位，得到一个新的函数的图像．(1)求这个新的函数的解析式；(2)若平移前后的这两个函数图象分别与y 轴交于O 、A 两点，与直线x =C 、B 两点．试判断以A 、B 、C 、O 四点为顶点的四边形形状，并说明理由；(3)若⑵中的四边形（不包括边界）始终覆盖着二次函数21222++-=b bx x y 的图象的一部分，求满足条件的实数b 的取值范围．11. （2010崇文一模） 2５．已知抛物线21y ax bx =++经过点A （1，3）和点B （2，1）．（1）求此抛物线解析式；（2）点C 、D 分别是x 轴和y 轴上的动点，求四边形ABCD 周长的最小值；（3）过点B 作x 轴的垂线，垂足为E 点．点P 从抛物线的顶点出发，先沿抛物线的对称轴到达F 点,再沿FE 到达E 点，若P 点在对称轴上的运动速度是它在直线FE ,试确定点F 的位置,使得点P 按照上述要求到达E 点所用的时间最短．（要求：简述确定F 点位置的方法，但不要求证明）12（2010崇文一模）23．已知P （3,m -)和Q （1，m ）是抛物线221y x bx =++上的两点．（1）求b 的值；（2）判断关于x 的一元二次方程221x bx ++=0是否有实数根，若有，求出它的实数根；若没有，请说明理由；（3）将抛物线221y x bx =++的图象向上平移k （k 是正整数）个单位，使平移后的图象与x 轴无交点，求k 的最小值．13.（2010朝阳二模）25．（本小题8分）如图，边长为2的正方形ABCO 中，点F 为x 轴上一点，CF=1，过点B 作BF 的垂线，交y 轴于点E ． （1）求过点E 、B 、F 的抛物线的解析式；（2）将∠EBF 绕点B 顺时针旋转，角的一边交y 轴正半轴于点M ，另一边交x 轴于点N ，设BM 与（1）中抛物线的另一个交点为点G ，且点G 的横坐标为56，EM 与NO 有怎样的数量关系？请说明你的结论．（3）点P 在（1）中的抛物线上，且PE 与y 轴所成锐角的正切值为23，求点P 的坐标．14（2010朝阳二模）22．（本小题5分）已知抛物线222m mx x y +-=与直线x y 2=交点的横坐标均为整数，且2＜m ，求满足要求的m 的整数值．15.（2010东城二模）24．如图，二次函数过A （0，m ）、B （3-，0）、C （12，0），过A 点作x 轴的平行线交抛物线于一点D ，线段OC 上有一动点P ，连结DP ，作PE ⊥DP ，交y 轴于点E ． （1）求AD 的长；（2）若在线段OC 上存在不同的两点P 1、P 2，使相应的点1E 、2E 都与点A 重合，试求m 的取值范围．（3）设抛物线的顶点为点Q ，当6090BQC ︒≤∠≤︒时，求m 的变化范围．16.（2010海淀二模）23. 已知：抛物线2(2)2y x a x a =+--(a 为常数. 且0a >). (1) 求证：抛物线与x 轴有两个交点；(2)x 轴的两个交点分别为A 、B (A 在B 左侧). 与y 轴的交点为C .① 当AC =. 求抛物线的解析式； ② 将①中的抛物线沿x 轴正方向平移t 个单位(t >0). 同时将直线l :3y x =沿y 轴正方向平移t 个单位.平移后的直线为'l . 移动后A 、B 的对应点分别为'A 、'B .当t 为何值时. 在直线'l 上存在点P . 使得△''A B P 为以''B A 为直角边的等腰直角三角形?17（2010海淀二模）25.如图. 在平面直角坐标系xOy 中. 点B 点D 在x 轴的正半轴上. 30ODB ∠=︒. OE 为△BOD 的中线. 过B 、E 两点的抛物线2y axc=+与x 轴相交于A 、F两点(A 在F 的左侧). (1) 求抛物线的解析式；(2) 等边△OMN 的顶点M 、N 在线段AE 上. 求AE 及AM 的长； (3) 点P 为△ABO 内的一个动点. 设m PA PB PO =++.请直接写出m 的最小值, 以及m 取得最小值时, 线段AP 的长. (备用图)18（2010石景山二模）23. 已知关于x 的一元二次方程()0312=-+--m x m x . (1) 求证：不论m 取何值时，方程总有两个不相等的实数根.(2) 若直线()31+-=x m y 与函数m x y +=2的图象1C 的一个交点的横坐标为2,求关于x 的一元二次方程()0312=-+--m x m x 的解.(3) 在(2)的条件下，将抛物线()312-+--=m x m x y 绕原点旋转︒180，得到图象2C ，点P 为x 轴上的一个动点，过点P 作x 轴的垂线，分别与图象1C 、2C 交于N M 、两点，当线段MN 的长度最小时，求点P 的坐标.19.（2010石景山二模）25. 已知：如图，抛物线2552++-=b ax ax y 与直线b x y +=21交于点)0,3(-A 、点B ，与y 轴交于点C .(1) 求抛物线与直线的解析式；(2) 在直线AB 上方的抛物线上有一点D ，使得△DAB 的面积是8，求点D 的坐标； (3) 若点P 是直线1=x 上一点，是否存在△PAB 是等腰三角形.若存在， 求出所有符合条件的点P 的坐标；若不存在，请说明理由.20（2010西城二模）23．已知：关于x 的一元二次方程04)4(2=-++-m x m x ，其中40<<m ．（1）求此方程的两个实数根（用含m 的代数式表示）；（2）设抛物线c bx x y ++-=2与x 轴交于A 、B 两点（A 在B 的左侧），若点D 的坐标为（0，-2），且AD ·BD =10，求抛物线的解析式；（3）已知点E （a ，1y ）、F （2a ，y 2）、G （3a ，y 3）都在（2）中的抛物线上，是否存在含有1y 、y 2、y 3，且与a 无关的等式？如果存在，试写出一个，并加以证明；如果不存在，说明理由．21. （2010西城二模）25． 在平面直角坐标系中，将直线l ：2343--=x y 沿x 轴翻折，得到一条新直线与x 轴交于点A ，与y 轴交于点B ，将抛物线1C ：232x y 沿x 轴平移，得到一条新抛物线2C 与y 轴交于点D ，与直线AB 交于点E 、点F ． （1）求直线AB 的解析式；（2）若线段DF ∥x 轴，求抛物线2C 的解析式；（3）在（2）的条件下，若点F 在y 轴右侧，过F 作FH ⊥x 轴于点G ，与直线l 交于点H ，一条直线m （m 不过△AFH 的顶点）与AF 交于点M ，与FH 交于点N ，如果直线m 既平分△AFH 的面积，求直线m 的解析式．22. （2010宣武二模）25. 对于任意两个二次函数: y 1=a 1x+b 1x+c 1; y 2=a 2x+b 2x+c 2, 其中a 1∙a 2≠0. 当Ⅰa 1Ⅰ=Ⅰa 2Ⅰ时, 我们称这两个二次函数的图象为全等抛物线. 现有△ABM, A(-1,0) B(1,0). 我们记过三点的二次函数的图象为“C□□□”(“□□□”中填写相应三个点的字母). 如过点A 、B 、M 三点的二次函数的图像为CABM.(1) 如果已知M(0,1), △ABM≌△ABN. 请通过计算判断CABM 与CABN 是否为全等抛物线;(2) ① 若已知M(0, n), 在图中的平面直角坐标系中, 以A 、B 、M 三点为顶点, 画出平行四边形. 求抛物线CABM 的解析式, 然后请直接写出所有过平行四边形中三个顶点且能与CABM 全等的抛物线解析式. ② 若已知M(m,n), 当m,n 满足什么条件时, 存在抛物线CABM? 根据以上的探究结果, 在图中的平面直角坐标系中, 以A 、B 、M 三点为顶点, 画出平行四边形. 然后请列出所有满足过平行四边形中三个顶点且能与CABM 全等的抛物线C□□□”.23.（2010丰台二模）23．（本小题满分7分）已知：关于x 的一元二次方程0)1(222=++-m x m x 有两个整数根，m <5且m 为整数． （1）求m 的值；（2）当此方程有两个非零的整数根时，将关于x 的二次函数22)1(2m x m x y ++-=的图象沿x 轴向左平移4个单位长度，求平移后的二次函数图象的解析式； （3）当直线y =x +b 与（2）中的两条抛物线有且只有三个．．交点时，求b 的值．24（2010丰台二模）25．（本小题满分8分）已知：如图，四边形OABC 是矩形，4OA =，8OC =，将矩形OABC 沿直线AC 折叠，使点B 落在点D 处，AD 交OC 于点E ． （1）求OE 的长；（2）求过O D C ，，三点的抛物线的解析式；（3）若F 为过O D C ，，三点的抛物线的顶点，一动点P 从点A 出发，沿射线AB 以每秒1个单位长度的速度匀速运动，当运动时间t （秒）为何值时，直线PF 把FAC △分成面积之比为1:3的两部分？25（2010崇文二模）24．如图，在平面直角坐标系中，O 是坐标原点，点A 、B 的坐标分别为A(0,3)和B(5,0)，连结AB ．（1）现将△AOB 绕点O 按逆时针方向旋转90°，得到△COD ，（点A 落到点C 处），请画出△COD ，并求经过B, C, D 三点的抛物线对应的函数关系式；（2）将（1）中抛物线向右平移两个单位，点B 的对应点为点E ，平移后的抛物线与原抛物线相交于点F ．P 为平移后的抛物线对称轴上一个动点，连结PE , PF ，当PE-PF 的绝对值取得最大值时，求点P 的坐标；（3）在（2）的条件下，当点P 在抛物线对称轴上运动时，是否存在点P 使△EPF 为直角三角形？如果存在，请求出点P 的坐标；如果不存在，请说明理由．26（2010崇文二模）23．已知一元二次方程2 10x px q +++=的一根为 2．（1）求q 关于p 的函数关系式；（2）求证：抛物线2 y x px q =++与x 轴有两个交点；（3）设抛物线2 1y x px q =+++与x 轴交于A 、B 两点（A 、B 不重合），且以AB 为直径的圆正好经过该抛物线的顶点．求,p q 的值．2009年北京中考数学模拟分类——二次函数综合题27.（2009朝阳一模）24. 抛物线与x 轴交于A （－1，0）、B 两点，与y 轴交于点C （0，－3），抛物线顶点为M ，连接AC 并延长AC 交抛物线对称轴于点Q ，且点Q 到x 轴的距离为6. （1）求此抛物线的解析式；（2）在抛物线上找一点D ，使得DC 与AC 垂直，求出点D 的坐标；（3）抛物线对称轴上是否存在一点P ，使得S △PAM =3S △ACM ，若存在，求出P 点坐标；若不存在，请说明理由.28.（2009东城一模）24．(本题满分7分)在平面直角坐标系中，现将一块等腰直角三角板ABC 放在第二象限，斜靠在两坐标轴上，且点A (0，2)，点C (－1，0)，如图所示，抛物线y ＝ax 2＋ax －2经过点B ．(1)求点B 的坐标； (2)求抛物线的解析式；(3)在抛物线上是否还存在点P (点B 除外)，使△ACP 仍然是以AC 为直角边的等腰直角三角形?若存在，求所有点P 的坐标；若不存在，请说明理由．29（2009丰台一模）25．已知抛物线223y x bx c =-++与x 轴交于不同的两点()10A x ，和()20B x ，，与y 轴交于点C ，且12x x ，是方程2230x x --=的两个根（12x x <）．（1）求抛物线的解析式；（2）过点A 作AD ∥CB 交抛物线于点D ，求四边形ACBD 的面积； （3）如果P 是线段AC 上的一个动点（不与点A 、C 重合），过点P 作平行于x 轴的直线l 交BC 于点Q ，那么在x 轴上是否存在点R ，使得△PQR 为等腰直角三角形？若存在，求出点R 的坐标；若不存在，请说明理由．30.（2009海淀一模）25．已知抛物线经过点A (0，4)、B (1，4)、C (3，2)，与x 轴正半轴交于点D ．(1)求此抛物线的解析式及点D 的坐标；(2)在x 轴上求一点E ，使得△BCE 是以BC 为底边的等腰三角形；(3)在(2)的条件下，过线段ED 上动点P 作直线PF ∥BC ，与BE 、CE 分别交于点F 、G ，将△EFG 沿FG 翻折得到△E ′FG ．设P (x ，0)，△E ′FG 与四边形FGCB 重叠部分的面积为S ，求S 与x 的函数关系式及自变量x 的取值范围．31.（2009西城一模）24．已知：如图，在平面直角坐标系xOy 中，直线643+-=x y 与x 轴、y 轴的交点分别为A、B，将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x轴于点C．(1)直接写出点C的坐标，并求过A、B、C三点的抛物线的解析式；(2)若抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形?若存在，求出点P的坐标；若不存在，说明理由；(3)设抛物线的对称轴与直线BC的交点为T，Q为线段BT上一点，直接写出｜QA－QO｜的取值范围．32.（2009宣武一模）25．如图，矩形OABC的边OC、OA分别与x轴、y轴重合，点B的坐标是(3，1)，点D是AB边上一个动点(与点A不重合)，沿OD将△OAD翻折后，点A落在点P处．(1)若点P在一次函数y＝2x－1的图象上，求点P的坐标；(2)若点P在抛物线y＝ax2图象上，并满足△PCB是等腰三角形，求该抛物线解析式；(3)当线段OD与PC所在直线垂直时，在PC所在直线上作出一点M，使DM＋BM最小，并求出这个最小值．33.（2009崇文一模）24．(本小题满分7分)如图，抛物线y＝ax2＋bx－3，与x轴交于A，B两点，与y轴交于点C，且OB＝OC＝3OA．(Ⅰ)求抛物线的解析式；(Ⅱ)探究坐标轴上是否存在点P ，使得以点P ，A ，C 为顶点的三角形为直角三角形?若存在，求出P 点坐标，若不存在，请说明理由； (Ⅲ)直线131+-=x y 交y 轴于D 点，E 为抛物线顶点．若∠DBC ＝α ，∠CBE ＝β ，求α －β 的值．34（2009石景山一模）21．已知：如图，直角三角形AOB 的两直角边OA 、OB 分别在x 轴的正半轴和y 轴的负半轴上，C 为线段OA 上一点，OC ＝OB ，抛物线y ＝x 2－(m ＋1)x ＋m (m 是常数，且m ＞1)经过A 、C 两点．(1)求出A 、B 两点的坐标(可用含m 的代数式表示)： (2)若△AOB 的面积为2，求m 的值．35.（2009朝阳二模）23．（本小题7分）如图，点A 在x 轴的负半轴上，OA=4，将△ABO绕坐标原点O 顺时针旋转90°，得到△O B A 11，再继续旋转90°，得到△O B A 22.抛物线y= ax 2+bx+3经过B 、1B 两点.（1）求抛物线的解析式；（2）点2B 是否在此抛物线上，请说明理由；（3）在该抛物线上找一点P ，使得△2PBB 是以2BB 为底的等腰三角形，求出所有符合条件的点P 的坐标； （4）在该抛物线上，是否存在两点M 、N ，使得原点O 是线段MN 的中点，若存在，直接写出这两点的坐标；若不存在，请说明理由.36.（2009崇文二模）25．（本小题满分８分）在平面直角坐标系中，抛物线c x ax y ++=2经过直线42+=x y 与坐标轴的两个交点B C 、，它与x 轴的另一个交点为A ．点N 是抛物线对称轴与x 轴的交点，点M 为线段AB 上的动点． （1）求抛物线的解析式及点A 的坐标；（2）如图①，若过动点M 的直线BC ME //交抛物线对称轴于点E ．试问抛物线上是否存在点F ，使得以点F E N M ,,,为顶点组成的四边形是平行四边形，若存在，求出点F 的坐标；若不存在，说明理由； （3）如图②，若过动点M 的直线AC MD //交直线BC 于D ，连接CM ．当CDM ∆的面积最大时，求点M 的坐标？图1 图237.（2009东城二模）24. 定义{},,a b c 为函数2y ax bx c =++的 “特征数”．如：函数223y x x =-+的“特征数”是{}1,2,3-，函数23y x =+的“特征数”是{}0,2,3,函数y x =-的“特征数”是{}0,1,0-（1）将“特征数”是⎪⎭⎪⎬⎫⎩⎨⎧1,33,0的函数图象向下平移2个单位，得到一个新函数，这个新函数的解析式；（2）在（1）中，平移前后的两个函数分别与y 轴交于A 、B 两点，与直线3=x 分别交于D 、C 两点，判断以A 、B 、C 、D 四点为顶点的四边形形状,请说明理由并计算其周长．（3）若（2）中的四边形与“特征数”是211,2,2b b ⎧⎫-+⎨⎬⎩⎭的函数图象的有交点，求满足条件的实数 b 的取值范围？38（2009海淀二模）23、已知：关于x 的一元二次方程x 2＋（n －2m ）x ＋m 2－mn=0①(1)、求证：方程①有两个实数根： （2）、若m －n －1=0,求证方程①有一个实数根为1； （3）、在（2）的条件下，设方程①的另一个根为a 。

海 淀 区 九 年 级 第 二 学 期 期 中 测评数 学2010.5考生须知1．本试卷共5页，共五道大题，25道小题，满分120分.考试时间120分钟. 2．在答题卡上准确填写学校名称、班级名称、姓名.3．试题答案一律填涂或书写在答题纸上，在试卷上作答无效. 4．考试结束，请将本试卷、答题纸和草稿纸一并交回. 一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．1．的倒数是A. 2B.C.D.2．2010年2月12日至28日，温哥华冬奥会官方网站的浏览量为275 000 000人次. 将 275 000 000用科学记数法表示为 A.B.C.D.3．右图是某几何体的三视图，则这个几何体是A . 圆柱B . 正方体C . 球D . 圆锥4．一个多边形的内角和是外角和的2倍，则这个多边形的边数为A . 5B .6C . 7D . 85．一个布袋中有4个除颜色外其余都相同的小球，其中3个白球，1个红球．从袋中任意摸出1个球是白球的概率是A ．B ．C ．D ．6． 四名运动员参加了射击预选赛，他们成绩的平均环数及其方差如表所示．如果选出一个成绩较好且状态稳定的人去参赛，那么应选 A ．甲 B ．乙 C ．丙 D ．丁 7．把代数式分解因式，结果正确的是A．B．C．D．8. 如图,点、是以线段为公共弦的两条圆弧的中点，. 点、分别为线段、上的动点. 连接、，设，，下列图象中，能表示与的函数关系的图象是A． B．C． D．二、填空题（本题共16分，每小题4分）9．函数的自变量的取值范围是．10．如图, 的半径为2，点为上一点，弦于点，,则________．11．若代数式可化为，则的值是．12. 如图，+1个边长为2的等边三角形有一条边在同一直线上，设△的面积为，△的面积为，…，△的面积为，则= ；=____ （用含的式子表示）．三、解答题（本题共30分，每小题5分）13．计算：．14．解方程：．15. 如图, △和△均为等腰直角三角形，, 连接、.求证: .16．已知：，求代数式的值.17. 已知：如图，一次函数与反比例函数的图象在第一象限的交点为．（1）求与的值；（2）设一次函数的图像与轴交于点，连接，求的度数．18. 列方程（组）解应用题：2009年12月联合国气候会议在哥本哈根召开．从某地到哥本哈根，若乘飞机需要3小时，若乘汽车需要9小时．这两种交通工具平均每小时二氧化碳的排放量之和为70千克，飞机全程二氧化碳的排放总量比汽车的多54千克，分别求飞机和汽车平均每小时二氧化碳的排放量．四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）19．已知：如图，在直角梯形中，∥，，于点O，，求的长.20.已知：如图，为的外接圆，为的直径，作射线，使得平分，过点作于点.（1）求证：为的切线；（2）若，，求的半径.21.2009年秋季以来，我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分.图1 图2请根据以上信息解答问题：（1）补全图1和图2；（2）如果全校学生家庭总人数约为3000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量.22．阅读：如图1，在和中，,,、、、四点都在直线上，点与点重合.连接、，我们可以借助于和的大小关系证明不等式：（）.证明过程如下:∵∴∵,∴.即.∴.∴.解决下列问题：（1）现将△沿直线向右平移，设,且.如图2,当时, .利用此图,仿照上述方法,证明不等式：（）.（2）用四个与全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式.请你画出一个示意图，并简要说明理由.五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23．关于的一元二次方程有实数根，且为正整数.（1）求的值；（2）若此方程的两根均为整数，在平面直角坐标系中,抛物线与轴交于、两点（在左侧），与轴交于点.点为对称轴上一点，且四边形为直角梯形，求的长；（3）将（2）中得到的抛物线沿水平方向平移，设顶点的坐标为,当抛物线与（2）中的直角梯形只有两个交点，且一个交点在边上时，直接写出的取值范围.24. 点为抛物线(为常数，)上任一点，将抛物线绕顶点逆时针旋转后得到的新图象与轴交于、两点（点在点的上方），点为点旋转后的对应点.（1）当，点横坐标为4时，求点的坐标；（2）设点，用含、的代数式表示；（3) 如图，点在第一象限内, 点在轴的正半轴上，点为的中点，平分，，当时，求的值.25.已知：中，，中，,.连接、，点、、分别为、、的中点.图1 图2(1) 如图1，若、、三点在同一直线上，且，则的形状是________________，此时________；(2) 如图2，若、、三点在同一直线上，且，证明，并计算的值（用含的式子表示）；(3) 在图2中，固定，将绕点旋转，直接写出的最大值.海淀区九年级第二学期期中测评数学试卷答案及评分参考一、选择题（本题共32分，每小题4分）题号 1 2 3 4 5 6 7 8 答案 B C D B A B D C 二、填空题（本题共16分，每小题4分）题号9 10 11 12答案60 5三、解答题（本题共30分，每小题5分）13．计算：.解：原式=----------------------------------4分=.---------------------------------5分14．解方程：.解：去分母，得．---------------------------------1分去括号，得．---------------------------------2分解得．---------------------------------4分经检验，是原方程的解．∴原方程的解是．---------------------------------5分15．证明：∵∴---------------------------------1分∵△与△均为等腰三角形，∴---------------------------------3分在△和△中，∴△≌△.---------------------------------4分∴.---------------------------------5分16．解：原式=---------------------------------2分=.---------------------------------3分当时，原式=---------------------------------4分.---------------------------------5分17．解：（1）∵点在双曲线上，∴.---------------------------------1分又∵在直线上，∴.---------------------------------2分（2）过点A作AM⊥x轴于点M.∵直线与轴交于点，∴.解得.∴点的坐标为.∴.---------------------------------3分∵点的坐标为，∴.在Rt△中，,∴.∴.---------------------------------4分由勾股定理，得.∴∴.∴.---------------------------------5分18．解：设乘飞机和坐汽车每小时的二氧化碳排放量分别是x千克和y千克. ………1分依题意，得---------------------------------2分解得----------------------------4分答: 飞机和汽车每小时的二氧化碳排放量分别是57千克和13千克. ………5分四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）19．解法一：过点作交的延长线于点.---------------------------------1分∴.∵于点,∴.∴. ---------------2分∵，∴四边形为平行四边形. ---------------3分∴.∵，∴.-------------------------------4分∵，∴.∴.---------------------------------5分解法二：，.又，. --------------------------------------------1分于点,....------------------------------------------2分.---------------------------------------------3分在Rt△中，.在Rt△中，..------------------------------------------4分,，. ---------------------------------------------5分20. （1）证明：连接. ---------------------------------1分∵，∴.∵，∴.∴ .∴∥.--------------------------2分∵,∴.∴.∵是⊙O半径，∴为⊙O的切线. ---------------------------------3分（2）∵,，，∴.由勾股定理，得. --------------------------------4分∴.∵是⊙O直径，∴.∴.又∵, ,∴.在Rt△中，==5.∴的半径为.-------------------------5分21. 解：(1)-------------------------2分--------------------------4分(2) 全体学生家庭月人均用水量为--------------------------5分（吨）.答：全校学生家庭月用水量约为9040吨.--------------------------6分22．（1）；--------------------------1分证明：连接、.可得.∴，.∵，∴，即.∴.∴.--------------------------2分（2）答案不唯一，图1分，理由1分.举例：如图，理由：延长BA、FE交于点I.∵，∴，即.∴.∴.--------------------------4分举例：如图，理由：四个直角三角形的面积和，大正方形的面积.∵，∴.∴.--------------------------4分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23．解：（1）∵关于的一元二次方程有实数根，∴△=.∴-----------------------1分又∵为正整数，∴. ------------------- 2分（2）∵方程两根均为整数，∴.---------------3分又∵抛物线与x轴交于A、B两点，∴.∴抛物线的解析式为.--------------4分∴抛物线的对称轴为.∵四边形为直角梯形，且，∴∥.∵点在对称轴上，∴.--------------5分（3）或.----------- 7分（写对一个给1分）24. 解：（1）当m=2时，，则，. --------------------1分如图，连接、,过点作轴于,过点作轴于.依题意,可得△≌△.则∴.∴. ------------------2分（2）用含的代数式表示：. ------4分（3）如图，延长到点E，使,连接.∵为中点,∴.∵,∴△≌△.∴. ------------------5分∵,∴.∵平分,∴.∴△≌△. ------------------6分∴.∴.------------------7分∵在新的图象上,∴.∴，（舍）.∴. ------------------8分25. 解：(1)等边三角形，1；(每空1分) ------------------------2分（2）证明：连接、.由题意，得，,.∵、、三点在同一直线上，∴、、三点在同一直线上.∴.∵为中点，∴在Rt△中，.在Rt△中，.∴.---------------------------3分∴、、、四点都在以为圆心，为半径的圆上.∴.又∵，∴.∴. ----------------------------------4分∴.由题意，，又.∴.------------------------------------5分∴.在Rt中，.∵，∴.∴.------------------------------6分（3）.--------------------------------7分(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。

(2010高三海淀一模)（12分）A 、B 、C 是三种常见短周期元素的单质。

常温下D 为无色液体，E 是一种常见的温室气体。

其转化关系如图（反应条件和部分产物略去）。

试回答：（1）E 的电子式是___________。

（2）单质X 和B 或D 均能反应生成黑色固体Y ，Y 的化学式是_________________。

（3）物质Z 常用于对空气进行杀菌、净化和水果保鲜等。

Z 和B 的组成元素相同，Z分子中各原子最外层电子数之和为18。

Z 和酸性碘化钾溶液反应生成B 和碘单质，反应的离子方程式是______________。

（4）取0.3 mol F 与足量D 充分混合后，所得溶液中再通入0.2 mol E 充分反应，最后得到的水溶液中各种离子的浓度由大到小的顺序是（不考虑H +）_______________________。

（5）E 的大量排放会引发很多环境问题。

有科学家提出，用E 和H 2合成CH 3OH 和H 2O ，对E 进行综合利用。

25 ℃，101 kPa 时该反应的热化学方程式是___________________________。

（已知甲醇的燃烧热ΔH = -726.5 kJ ·mol -1，氢气的燃烧热ΔH = -285.8 kJ ·mol -1）( 2010高三东城一模)（14分）短周期元素X 、Y 、Z 、M 、N 原子序数依次增大，有关信息如下：（1）XY 2的电子式是 ▲ ；Z 2Y 2中所含化学键类型是▲；XY 2与Z 2Y 2反应的化学方程式是 ▲ 。

（2）恒容条件下，一定量的NY 2、Y 2发生反应：2NY 2（g ）+Y 2（g ）2NY 3（g ）。

温度分别为T 1和T 2时，NY 3的体积分数随时间变化如右图。

该反应的ΔH▲0（填“>”、“<”或“=”，下同）；若T1、T2时该反应的化学平衡常数分别为K1、K2，则K1▲K2。

海淀区初三一模语文答案作者: 日期:海淀区九年级第二学期期中练习语文参考答案及评分标准2015.5一、基础.运用（共22分）1. （1）B （2 分）（2）C （2 分）（3）C （2 分）（4）D （2 分）（5）A （2 分）2 . C （2 分）3. （1） D （2分）（2）长风破浪会有时，直挂云帆济沧海（2分。

每空1分，该空有错不得分）4. ①日月之行，若出其中（2分。

每空1分，该空有错不得分）②煮酒论英雄（青梅煮酒）（1分，意思对即可）③关羽（1分）④罗贯中（1分）⑤白（1分）二、文言文阅读（共12分）5. C （2 分）6. （1）完成（1分）（2）称为（叫，叫做）（1分）7. （1）用纸条给它做标记。

（2分）（2）天下的书籍（于是）就多了起来。

（2分）8. （1）字印活（字活，字模活）（1分）（2）印刷活（备版活、字印数目活）（1分）（3）学者艰于传录（1分）（4）人皆惮其工费（板木工匠，所费甚多；功力不及，数载难成）（1分）三、现代文阅读（共36分）（一）（共16 分）9. 答案示例：（1）将军战功卓著，步步晋升，升任200师师长，身先士卒，治军有方。

（治军有方）（2）将军率200师奉命镇守昆仑关，与日军苦战，赢得胜利。

（昆仑关大捷）（3）将军指挥军队在同古顽强阻击数倍与己的日军精锐部队，同古城安如磐石。

（誓死守卫同古）（4）将军欲率余部突出日军封锁线回国，途中不幸受伤牺牲。

（以身殉国）（共4分。

每空1分，答出要点，意思对即可。

）10. 答案示例：第⑨段通过记叙将军的遗书，将军给子女命名，将军善待妻子；不仅揭示出将军的拳拳报国之心；而且也可见出他对家人的牵挂和爱； 使将军形象更为丰满感人。

（共3分。

内容1 分，作用2分。

）11. 甲（共2分。

） 12.略（共2分。

）13. 答案示例一：第⑥段用“轮番轰炸”、“火海”等词语，写出战斗的惨烈，烘托将军的勇敢；用 排比描写我军灵活机智地阻击敌人的炮轰、步兵等进攻，彰显将军指挥的从容、有谋 略；用动作“缓缓站起”，语言“余战死，以副师长代理……”，表明将军以死报国的决心。