2010年北京海淀数学一模试卷及答案

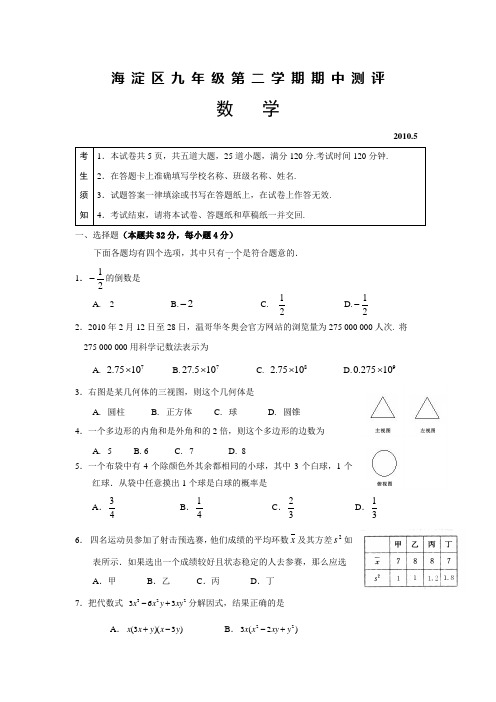
海 淀 区 九 年 级 第 二 学 期 期 中 测 评数 学2010.5 考生须知 1．本试卷共5页，共五道大题，25道小题，满分120分.考试时间120分钟. 2．在答题卡上准确填写学校名称、班级名称、姓名. 3．试题答案一律填涂或书写在答题纸上，在试卷上作答无效.4．考试结束，请将本试卷、答题纸和草稿纸一并交回. 一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．21-的倒数是 A. 2 B.2- C.21 D.21- 2．2010年2月12日至28日，温哥华冬奥会官方网站的浏览量为275 000 000人次. 将 275 000 000用科学记数法表示为A. 72.7510⨯ B.727.510⨯ C. 82.7510⨯ D.90.27510⨯ 3．右图是某几何体的三视图，则这个几何体是A . 圆柱B . 正方体C . 球D . 圆锥 4．一个多边形的内角和是外角和的2倍，则这个多边形的边数为A . 5B .6C . 7D . 85．一个布袋中有4个除颜色外其余都相同的小球，其中3个白球，1个红球．从袋中任意摸出1个球是白球的概率是 A ．43 B ．41 C ．32 D ．316． 四名运动员参加了射击预选赛，他们成绩的平均环数x 及其方差2s 如表所示．如果选出一个成绩较好且状态稳定的人去参赛，那么应选 A ．甲 B ．乙 C ．丙 D ．丁 7．把代数式 322363x x y xy -+分解因式，结果正确的是A ．(3)(3)x x y x y +-B ．223(2)x x xy y -+C ．2(3)x x y +D ．23()x x y -8. 如图,点E 、F 是以线段BC 为公共弦的两条圆弧的中点，6BC =. 点A 、D 分别为线段EF 、BC 上的动点. 连接AB 、AD ，设BD x =，22AB AD y -=，下列图象中，能表示y 与x 的函数关系的图象是A ．B ．C ．D ．二、填空题（本题共16分，每小题4分） 9．函数13-=x y 的自变量x 的取值范围是 ．10．如图,O 的半径为2，点A 为O 上一点，OD ⊥弦BC 于点D ， 1OD =,则BAC ∠=________︒．11．若代数式26x x b -+可化为2()1x a --，则b a -的值是 ．12. 如图，n +1个边长为2的等边三角形有一条边在同一直线上，设△211B D C 的面积为1S ，△322B D C 的面积为2S ，…，△1n n n B D C +的面积为n S ，则2S = ；n S =____ （用含n 的式子表示）．三、解答题（本题共30分，每小题5分） 13011122cos30(31)()2-︒+- ．14．解方程：23233x x x +=-+．15. 如图, △OAB 和△COD 均为等腰直角三角形，90AOB COD ∠=∠=︒, 连接AC 、BD .求证: AC BD =.FE A BDO CADCOB AODCB A16． 已知：2310x x +=，求代数式2(2)(10)5x x x -++-的值.17. 已知：如图，一次函数33y x m =+与反比例函数3y x=的图象在第一象限的交点为(1)A n ，．（1）求m 与n 的值；（2）设一次函数的图像与x 轴交于点B ，连接OA ，求BAO ∠的度数．18. 列方程（组）解应用题：2009年12月联合国气候会议在哥本哈根召开．从某地到哥本哈根，若乘飞机需要3小时，若乘汽车需要9小时．这两种交通工具平均每小时二氧化碳的排放量之和为70千克，飞机全程二氧化碳的排放总量比汽车的多54千克，分别求飞机和汽车平均每小时二氧化碳的排放量．四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分） 19．已知：如图，在直角梯形ABCD 中，AD ∥BC ，︒=∠90DCB ，BD AC ⊥于点O ，4,2==BC DC ，求AD 的长.20. 已知：如图，O 为ABC ∆的外接圆，BC 为O 的直径，作射线BF ，使得BA 平分CBF ∠，过点A 作AD BF ⊥于点D .（1） 求证：DA 为O 的切线； （2） 若1BD =，1tan 2BAD ∠=，求O 的半径.21. 2009年秋季以来，我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分.图1图2请根据以上信息解答问题： （1）补全图1和图2；（2）如果全校学生家庭总人数约为3000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量.22．阅读：如图1，在ABC ∆和DEF ∆中，90ABC DEF ∠=∠=︒,,AB DE a ==BC EF b == ()b a <,B 、C 、D 、 E 四点都在直线m 上，点B 与点D 重合.连接AE 、FC ，我们可以借助于ACE S ∆和FCE S ∆的大小关系证明不等式：222a b ab +>（0b a >>）.F OD CBA证明过程如下:∵,,.BC b BE a EC b a ===- ∴11(),22ACE S EC AB b a a ∆=⋅=- 11().22FCES EC FE b a b ∆=⋅=- ∵0b a >>, ∴FCE S ACE S ∆∆>. 即a ab b a b )(21)(21->-. ∴22b ab ab a ->-.∴222a b ab +>. 解决下列问题：（1）现将△DEF 沿直线m 向右平移，设()BD k b a =-,且01k ≤≤.如图2,当BD EC =时, k = .利用此图,仿照上述方法,证明不等式：222a b ab +>（0b a >>）. （2）用四个与ABC ∆全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式.请你画出一个．．示意图，并简要说明理由.五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．关于x 的一元二次方程240x x c -+=有实数根，且c 为正整数. （1）求c 的值；（2）若此方程的两根均为整数，在平面直角坐标系xOy 中,抛物线24y x x c =-+与x 轴交于A 、B 两点（A 在B 左侧），与y 轴交于点C . 点P 为对称轴上一点，且四边形OBPC 为直角梯形，求PC 的长；（3）将（2）中得到的抛物线沿水平方向平移，设顶点D 的坐标为(),m n ,当抛物线与（2）E图1F图2中的直角梯形OBPC 只有两个交点，且一个交点在PC 边上时，直接写出m 的取值范围.24. 点P 为抛物线222y x mx m =-+(m 为常数，0m >)上任一点，将抛物线绕顶点G 逆时针旋转90︒后得到的新图象与y 轴交于A 、B 两点（点A 在点B 的上方），点Q 为点P 旋转后的对应点.（1）当2m =，点P 横坐标为4时，求Q 点的坐标； （2）设点(,)Q a b ，用含m 、b 的代数式表示a ； （3) 如图，点Q 在第一象限内, 点D 在x 轴的正半轴上，点C为OD 的中点，QO 平分AQC ∠，2AQ QC =，当QD m =时，求m 的值.25.已知：AOB △中，2AB OB ==，COD △中，3CD OC ==,ABO DCO =∠∠. 连接AD 、BC ，点M 、N 、P 分别为OA 、OD 、BC 的中点.图1 图2(1) 如图1，若A 、O 、C 三点在同一直线上，且60ABO =∠，则PMN △的形状是________________，此时ADBC=________； (2) 如图2，若A 、O 、C 三点在同一直线上，且2ABO α=∠，证明PMN BAO △∽△，并计算ADBC的值（用含α的式子表示）； (3) 在图2中，固定AOB △，将COD △绕点O 旋转，直接写出PM 的最大值.。

平面解析几何一、选择题和填空题1．（海淀·理科·题13）已知有公共焦点的椭圆与双曲线中心为原点，焦点在x 轴上，左右焦点分别为12,F F ，且它们在第一象限的交点为P ，12PF F △是以1PF 为底边的等腰三角形．若110PF =，双曲线的离心率的取值范围为()1,2．则该椭圆的离心率的取值范围是 ．【解析】 12,35⎛⎫⎪⎝⎭；如图，设椭圆的半长轴长，半焦距分别为1,a c ，双曲线的半实轴长，半焦距分别为2,a c ，12,PF m PF n ==，则1222102m n a m n a m n c+=⎧⎪-=⎪⎨=⎪⎪=⎩1255a c a c =+⎧⇒⎨=-⎩，问题转化为已知125c c <<-，求5c c +的取值范围． 设5c x c =-，则51x c x =+，11521242c x c x x ==-+++． ∵12x <<，∴11111126242210x -<-<-+，即111232425x <-<+．2．（海淀·文科·题8）1by +=与圆221x y +=相交于A ，B 两点（其中,a b 是实数），且AOB ∆是直角三角形（O 是坐标原点），则点(),P a b 与点()0,1之间距离的最大值为（ ） A1 B ．2 CD1 【解析】 A ；圆221x y +=1by +=，∴2222a b +=， 即2212b a +=．因此所求距离为椭圆2212b a +=上点(),P a b 到焦点()0,11．3．（海淀·文科·题10）已知动点P 到定点()2,0的距离和它到定直线:2l x =-的距离相等，则点P 的轨迹方程为________． 【解析】 28y x =；由已知，该轨迹为2p =，定点为()0,0，对称轴为x 轴的抛物线，即28y x =．4．（丰台·文科·题4）直线0x y +=截圆224x y +=所得劣弧所对圆心角为（ ）A ．π6 B ．π3 C ．π2 D ．2π3【解析】 D ；1=2=，于是1cos22θ=，2π3θ=．5．（丰台·文科·题14）已知点()1,1A -，点()3,5B ，点P 是直线y x =上动点，当||||PA PB +的值最小时，点P 的坐标是 ． 【解析】 ()2,2；连结AB 与直线y x =交于点Q ，则当P 点移动到Q 点位置时，||||PA PB +的值最小．直线AB 的方程为()()515331y x ---=--，即340x y --=． 解方程组340x y y x --=⎧⎨=⎩，得22x y =⎧⎨=⎩．于是当||||PA PB +的值最小时，点P 的坐标为()2,2．6．（石景山·理·题5）（石景山·文·题5）经过点(2,3)P -作圆22(1)25x y ++=的弦AB ，使点P 为弦AB 的中点，则弦AB 所在直线方程为（ ） A ．50x y --= B ．50x y -+= C ．50x y ++= D ．50x y +-=【解析】 A ；设圆心为C ，则AB 垂直于CP ，3012(1)CP k --==---，故:32AB y x +=-，选A ．7．（西城·理·题13）（西城·文·题7）已知双曲线2213y x -=的左顶点为1A ，右焦点为2F ，P 为双曲线右支上一点，则12PA PF ⋅最小值为 _________ ． 【解析】 2-；12(1,0),(2,0)A F -，设(,)(1)P x y x ≥，2212(1,)(2,)2PA PF x y x y x x y ⋅=--⋅-=--+，又2213y x -=，故223(1)y x =-，于是2212114545816PA PF x x x ⎛⎫⋅=--=--- ⎪⎝⎭，当1x =时，取到最小值2-．8．（东城·理·题13）直线x t =过双曲线22221x y a b-=(0,0)a b >>的右焦点且与双曲线的两条渐近线分别交于A ，B 两点，若原点在以AB 为直径的圆外，则双曲线离心率的取值范围是 ．【解析】 (1,；,,,b b A t t B t t a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，要使原点在以AB 为直径的圆外，只需原点到直线AB 的距离t 大于半径b t a 即可，于是b a <，e c a ==e (1,∈．9．（东城·文·题7） 已知圆22104x y mx ++-=与抛物线214y x =的准线相切，则m 的值等于（ ）A ．BCD ． 【解析】 D ；抛物线的准线为1y =-，将圆化为标准方程222124m m x y +⎛⎫++= ⎪⎝⎭，圆心到直线的距离为1=m ⇒=10．（东城·文·题10）经过点(2,3)-且与直线250x y +-=垂直的直线方程为 ． 【解析】280x y -+=； 直线250x y +-=的斜率为2-，故所求直线的斜率为12，从而所求直线方程为13(2)2y x -=+．11．（东城·文·题14）点P 是椭圆2212516x y +=上一点，12,F F 是椭圆的两个焦点，且12PF F ∆的内切圆半径为1，当P 在第一象限时，P 点的纵坐标为 ．【解析】 83；121210,6PF PF F F +==，1212121211()18322PF F P P S PF PF F F F F y y ∆=++⋅==⋅=．12．（宣武·理·题6）若椭圆221x y m n+=与双曲线221(,,,x y m n p q p q -=均为正数）有共同的焦点1F ，2F ，P 是两曲线的一个公共点，则12||||PF PF ⋅等于（ ）A ．22p m -B ．p m -C ．m p -D ．22m p -【解析】 C ；由题设可知m n >，再由椭圆和双曲线的定义有12||||PF PF +=及12||||PF PF -=±两个式子分别平方再相减即可得12||||PF PF m p =-．13．（宣武·文·题8）设圆C 的圆心在双曲线2221(0)2x y a a -=>的右焦点且与此双曲线的渐近线相切，若圆C 被直线:0l x =截得的弦长等于2，则a 的值为（ ）A B C ．2D ．3【解析】 A ；圆C 的圆心C ，双曲线的渐近线方程为0ay ±=，C 到渐近线的距离为d ==故圆C 方程22(2x y +=．由l 被圆C 截得的弦长是2及圆C知，圆心C 到直线l 的距离为11a =⇒=14．（崇文·文·题4）若直线y x b =+与圆222x y +=相切，则b 的值为 （ ）A ．4±B ．2±C ．．±【解析】 B ；2b ==． 15．（朝阳·理·题6）已知点(3,4)P -是双曲线22221(0,0)x y a b a b-=>>渐近线上的一点，,E F 是左、右两个焦点，若0EP FP ⋅=，则双曲线方程为（ ） A ．22134x y -=B ．22143x y -=C ．221916x y -=D ．221169x y -=【解析】 C ；不妨设()(),0,,0E c F c -，于是有()()23,43,49160EP FP c c c ⋅=+-⋅--=-+=．于是225c =．排除A ，B ．又由D 中双曲线的渐近线方程为34y x =±，点P 不在其上．排除D ．16．（朝阳·理·题10）（朝阳·文·题13）圆224x y +=被直线0y +-=截得的劣弧所对的圆心角的大小为 ．【解析】 π3．圆心到直线的距离为d ==θ，于是cos2θ=π3θ=．17．（朝阳·文·题10）在抛物线22(0)y px p =>上，横坐标为4的点到焦点的距离为5，则p 的值为 ． 【解析】 2；由抛物线的几何性质，有4522pp +=⇒=．二、解答题18．（海淀·理科·题19）已知椭圆C 的中心在原点，焦点在x 轴上，左右焦点分别为1F ，2F ，且12||2F F =，点31,2⎛⎫⎪⎝⎭在椭圆C 上．⑴求椭圆C 的方程；⑵过1F 的直线l 与椭圆C 相交于A、B 两点，且2AF B ∆2F 为圆心且与直线l 相切的圆的方程．【解析】 ⑴设椭圆的方程为22221(0)x y a b a b+=>>，由题意可得：椭圆C 两焦点坐标分别为()11,0F -，()21,0F ．∴532422a ==+=．∴2a =，又1c =，2413b =-=，故椭圆的方程为22143x y +=．⑵当直线l x ⊥轴，计算得到：31,2A ⎛⎫-- ⎪⎝⎭，31,2B ⎛⎫- ⎪⎝⎭，21211||||32322AF B S AB F F ∆=⋅⋅=⨯⨯=，不符合题意．当直线l 与x 轴不垂直时，设直线l 的方程为：(1)y k x =+，由22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，消去y 得2222(34)84120k x k x k +++-=．显然0∆>成立，设11(,)A x y ，22(,)B x y ，则2122834k x x k +=-+，212241234k x xk -⋅=+．又||AB即2212(1)||34k AB k +==+，又圆2F 的半径r ==．所以2221112(1)||2234AF BkS AB rk∆+==⨯==+，化简，得4217180k k+-=，即22(1)(1718)0k k-+=，解得1k=±．所以，r==．故圆2F的方程为：22(1)2x y-+=．⑵另解：设直线l的方程为1x ty=-，由221143x tyx y=-⎧⎪⎨+=⎪⎩，消去x得22(43)690t y ty+--=，0∆>恒成立，设()11,A x y，()22,B x y，则122643ty yt+=+，122943y yt⋅=-+．所以12||y y-==又圆2F的半径为r==．所以212121||||2AF BS F F y y∆=⋅⋅-12||y y=-==21t=，所以r==故圆2F的方程为：22(1)2x y-+=．19．（海淀·文科·题19）已知椭圆C的对称中心为原点O，焦点在x轴上，离心率为12，且点31,2⎛⎫⎪⎝⎭0在该椭圆上．⑴求椭圆C的方程；⑵过椭圆C的左焦点1F的直线l与椭圆C相交于A、B两点，若AOB∆，求圆心在原点O且与直线l 相切的圆的方程．【解析】⑴设椭圆C的方程为22221x ya b+=(0)a b>>，由题意可得12cea==，又222a b c=+，所以2234b a=因为椭圆C经过31,2⎛⎫⎪⎝⎭，代入椭圆方程有22914134a a+=，解得2a=所以1c=，2413b=-=故椭圆C的方程为22143x y+=．⑵解法一：当直线l x⊥轴时，计算得到：31,2A⎛⎫-⎪⎝⎭，31,2B⎛⎫-⎪⎝⎭，1113||||13222AOBS AB OF∆=⋅⋅=⨯⨯=，不符合题意．当直线l与x轴不垂直时，设直线l的方程为：(1)y k x=+，0k≠由22(1)143y k xx y=+⎧⎪⎨+=⎪⎩，消去y，得2222(34)84120k x k x k+++-=显然0∆>成立，设()11,A x y，()22,B x y，则2122834kx xk+=-+，212241234kx xk-⋅=+又||AB=即2212(1)||34kABk+==+又圆O的半径r==所以1||2AOBS AB r∆=⋅⋅22112(1)234kk+=⋅+=化简，得4217180k k+-=，即22(1)(1718)0k k-+=，解得211k=，2218k=-（舍）所以r==O的方程为2212x y+=．⑵解法二：设直线l的方程为1x ty=-，由221143x tyx y=-⎧⎪⎨+=⎪⎩，消去x，得22(43)690t y ty+--=因为0∆>恒成立，设()11,A x y，()22,B x y，则12122269,4343ty yy yt t+=⋅=-++所以12||y y-==所以1121||||2AOBS F O y y∆=⋅⋅-==化简得到4218170t t--=，即22(1817)(1)0t t+-=，解得211,t=221718t=-（舍）又圆O的半径为r==所以r==O的方程为：2212x y+=20．（丰台·理科·题19）在直角坐标系xOy中，点M到点()1,0F，)2,0F的距离之和是4，点M的轨迹是C与x轴的负半轴交于点A，不过点A的直线:l y kx b=+与轨迹C交于不同的两点P和Q．⑴求轨迹C的方程；⑵当0AP AQ⋅=时，求k与b的关系，并证明直线l过定点．【解析】⑴∵点M到(),0，),0的距离之和是4，∴M的轨迹C是长轴为4，焦点在x轴上焦中为的椭圆，其方程为2214x y +=．⑵将y kx b =+，代入曲线C的方程，整理得22(14)40k x +++= 因为直线l 与曲线C 交于不同的两点P 和Q ，所以222222644(14)(44)16(41)0k b k b k b ∆=-+-=-+> ① 设()11,P x y ，()22,Q x y，则12x x +=，122414x x k =+ ② 且2212121212()()()()y y kx b kx b k x x kb x x b ⋅=++=+++ 显然，曲线C 与x 轴的负半轴交于点()2,0A -， 所以()112,AP x y =+，()222,AQ x y =+． 由0AP AQ ⋅=，得1212(2)(2)0x x y y +++=．将②、③代入上式，整理得22121650k kb b -+=． 所以(2)(65)0k b k b -⋅-=，即2b k =或65b k =．经检验，都符合条件①当2b k =时，直线l 的方程为2y kx k =+． 显然，此时直线l 经过定点()2,0-点． 即直线l 经过点A ，与题意不符．当65b k =时，直线l 的方程为6556y kx k k x ⎛⎫=+=+ ⎪⎝⎭．显然，此时直线l 经过定点6,05⎛⎫- ⎪⎝⎭点，且不过点A ．综上，k 与b 的关系是：65b k =，且直线l 经过定点6,05⎛⎫- ⎪⎝⎭点．21．（丰台·文科·题19）在直角坐标系xOy 中，点M到点()1,0F，)2,0F 的距离之和是4，点M 的轨迹是C ，直线:l y kx =轨迹C 交于不同的两点P 和Q ． ⑴求轨迹C 的方程；⑵是否存在常数k ，0OP OQ ⋅=？若存在，求出k 的值；若不存在，请说明理由． 【解析】 ⑴∵点M到(),0，),0的距离之和是4，∴M 的轨迹C 是长轴为4，焦点在x轴上焦距为的椭圆，其方程为2214x y +=．⑵将y kx =C 的方程，整理得22(14)40k x +++= ① 设()11,P x y ，()22,Q x y 由方程①，得12x x +=122414x x k =+ ②又(()2121212122y y kx kx k x x x x ⋅=+=++ ③ 若0OP OQ ⋅=，得12120x x y y += 将②、③代入上式，解得k =． 又因k 的取值应满足0∆>，即2410k ->（*），将k =代入（*）式知符合题意． 22．（石景山·理·题19）已知椭圆22221(0)x y a b a b+=>>:l y kx m =+交椭圆于不同的两点A ，B ． ⑴求椭圆的方程；⑵若m k =，且0OA OB ⋅=，求k 的值（O 点为坐标原点）； ⑶若坐标原点O 到直线lAOB △面积的最大值． 【解析】 ⑴设椭圆的半焦距为c，依题意c a a ⎧=⎪⎨⎪=⎩，解得c =由222a b c =+，得1b =∴所求椭圆方程为2213x y +=⑵∵m k =，∴(1)y kx k k x =+=+．设1122(,),(,)A x y B x y ，其坐标满足方程2213(1)x y y k x ⎧+=⎪⎨⎪=+⎩，消去y 并整理得2222(13)6330k x k x k +++-=，则()()()22226413330()k k k ∆=-+->*故22121222633,1313k k x x x x k k --+==++． ∵0OA OB ⋅=，∴12121212(1)(1)x x y y x x k x k x +=++⋅+2221212(1)()k x x k x x k =++++2222222223363(1)0131331k k k k k k k k k ---=++⋅+==+++∴k =，经检验k =满足(*)式．=223(1)4m k =+ 将y kx m =+代入椭圆方程，整理得222(13)6330k x kmx m +++-=222(6)4(13)(33)0()km k m ∆=-+->*∴2121222633,1313km m x x x x k k --+==++．∴2222222122223612(1)||(1)()(1)(31)31k m m AB k x x k k k ⎡⎤-=+-=+-⎢⎥++⎣⎦22222222212(1)(31)3(1)(91)(31)(31)k k m k k k k ++-++==++ 242221212123334(0)196123696k k k k k k =+=++=≠++⨯+++≤当且仅当2219k k =，即k =经检验，k =满足（*）式． 当0k =时，||AB =综上可知，max ||2AB =所以，当||AB 最大时，AOB △的面积取得最大值max 122S =⨯=．23．（石景山·文·题19）已知椭圆22221(0)x y a b a b+=>>，直线:l y kx m =+交椭圆于不同的两点A ，B ．⑴求椭圆的方程；⑵若1m =，且0OA OB ⋅=，求k 的值（O 点为坐标原点）； ⑶若坐标原点O 到直线lAOB △面积的最大值． 【解析】 ⑴设椭圆的半焦距为c，依题意c a a ⎧=⎪⎨⎪=⎩，解得c =由222a b c =+，得1b =∴所求椭圆方程为2213x y +=⑵∵1m =，∴1y kx =+．设1122(,),(,)A x y B x y ，其坐标满足方程221,3 1.x y y kx ⎧+=⎪⎨⎪=+⎩，消去y 并整理得22(13)60k x kx ++=，则()()22641300k k ∆=-+⨯>，解得0k ≠故121226,013kx x x x k -+=⋅=+． ∵0OA OB ⋅=，∴2121212121212(1)(1)(1)()1x x y y x x kx kx k x x k x x +=++⋅+=++++2222613(1)0101331k k k k k k --=+⨯+⋅+==++∴k =．=223(1)4m k =+．将y kx m =+代入椭圆方程，整理得222(13)6330k x kmx m +++-=()()()2226413330()km k m ∆=-+->*∴2121222633,1313km m x x x x k k --+==++ ∴2222222212223612(1)(1)()(1)(31)31k m m AB k x x k k k ⎡⎤-=+-=+-⎢⎥++⎣⎦22222222212(1)(31)3(1)(91)(31)(31)k k m k k k k ++-++==++242221212123334(0)196123696k k k k k k =+=++=≠++⨯+++≤． 当且仅当2219k k=，即k =时等号成立．经检验，k =满足()*式． 当0k =时，||AB =综上可知max 2AB =∴当AB 最大时，AOB △的面积取最大值122S =⨯=． 24．（西城·理·题18）椭圆C ：22221(0)x y a b a b+=>>⑴求椭圆C 的方程；⑵设过点D (0,4)的直线l 与椭圆C 交于,E F 两点，O 为坐标原点，若OEF △为直角三角形，求直线l 的斜率．【解析】 ⑴由已知225c a b a =+=， 又222a b c =+，解得224,1a b ==，所以椭圆C 的方程为2214x y +=；⑵根据题意，过点(0,4)D 满足题意的直线斜率存在，设:4l y kx =+， 联立22144x y y kx ⎧+=⎪⎨⎪=+⎩，消去y 得22(14)32600k x kx +++=，222(32)240(14)64240k k k ∆=-+=-，令0∆>，解得2154k >． 设E 、F 两点的坐标分别为1122(,),(,)x y x y ， ⅰ）当EOF ∠为直角时， 则1212223260,1414k x x x x k k +=-=++， 因为EOF ∠为直角，所以0OE OF ⋅=，即12120x x y y +=，所以21212(1)4()160k x x k x x ++++=，所以222215(1)32401414k k k k ⨯+-+=++，解得k =ⅱ）当OEF ∠或OFE ∠为直角时，不妨设OEF ∠为直角， 此时，1OE k k ⋅=，所以111141y y x x -⋅=-，即221114x y y =-……① 又221114x y +=…………② 将①代入②，消去1x 得2113440y y +-=，解得123y =或12y =-（舍去）， 将123y =代入①，得1x =所以114y k x -== 经检验，所求k 值均符合题意，综上，k的值为25．（西城·文·题18）椭圆C ：22221(0)x y a b a b+=>>(2,0)点．⑴求椭圆C 的方程；⑵设直线l ：y x m =+与椭圆C 交于,A B 两点，O 为坐标原点，若OAB ∆直角三角形，求m 的值．【解析】 ⑴已知241c a a ==，所以2,a c ==222a b c =+，所以1b =，所以椭圆C 的方程为2214x y +=．⑵联立2214x y y x m ⎧+=⎪⎨⎪=+⎩，消去y 得2258440x mx m ++-=，2226480(1)1680m m m ∆=--=-+，令0∆>，即216800m -+>，解得m <． 设A ，B 两点的坐标分别为1122(,),(,)x y x y ，i ）当AOB ∠为直角时，则21212844,55m x x m x x -+=-=，因为AOB ∠为直角，所以0OA OB ⋅=，即12120x x y y +=， 所以212122()0x x m x x m +++=，所以222888055m m m --+=，解得m =ii ）当OAB ∠或OBA ∠为直角时，不妨设OAB ∠为直角， 由直线l 的斜率为1，可得直线OA 的斜率为1-， 所以111y x =-，即11y x =-， 又2214x y +=，所以211514x x =⇒=1112m y x x =-=-=依题意m <，且0m ≠，经检验，所求m 值均符合题意，综上，m的值为26．（东城·理·题19）已知椭圆2222:1x y C a b+=(0)a b >>的离心率为12，以原点为圆心，椭圆的短半轴为半径的圆与直线0x y -相切．⑴求椭圆C 的方程；⑵设(4,0)P ，A ，B 是椭圆C 上关于x 轴对称的任意两个不同的点，连结PB 交椭圆C 于另一点E ，证明直线AE 与x 轴相交于定点Q ；⑶在⑵的条件下，过点Q 的直线与椭圆C 交于M ，N 两点，求OM ON ⋅的取值范围．【解析】 ⑴由题意知12c e a ==，所以22222214c a b e a a -===．即2243a b =．又因为b ==24a =，23b =． 故椭圆C 的方程为22143x y +=．⑵由题意知直线PB 的斜率存在，设直线PB 的方程为(4)y k x =-． 由22(4),1.43y k x x y =-⎧⎪⎨+=⎪⎩得2222(43)3264120k x k x k +-+-=． ①设点11(,)B x y ，22(,)E x y ，则11(,)A x y -． 直线AE 的方程为212221()y y y y x x x x +-=--． 令0y =，得221221()y x x x x y y -=-+．将11(4)y k x =-，22(4)y k x =-代入整理，得12121224()8x x x x x x x -+=+-．②由①得21223243k x x k +=+，2122641243k x x k -=+代入②整理，得1x =． 所以直线AE 与x 轴相交于定点(1,0)Q ．⑶当过点Q 直线MN 的斜率存在时，设直线MN 的方程为(1)y m x =-，且(,)M M M x y ，(,)N N N x y 在椭圆C 上． 由22(1)143y m x x y =-⎧⎪⎨+=⎪⎩得2222(43)84120m x m x m +-+-=．易知0∆>．所以22843M N m x x m +=+，2241243M N m x x m -=+，22943M N m y y m =-+．则M N M N OM ON x x y y ⋅=+2225125334344(43)m m m +=-=--++．因为20m ≥，所以21133044(43)m --<+≤． 所以54,4OM ON ⎡⎫⋅∈--⎪⎢⎣⎭．当过点Q 直线MN 的斜率不存在时，其方程为1x =．解得3(1,)2M ，3(1,)2N -．此时54OM ON ⋅=-． 所以OM ON ⋅的取值范围是54,4⎡⎤--⎢⎥⎣⎦．27．（东城·文·题19）已知椭圆C ：22221(0)x y a b a b+=>>，以原点为圆心，椭圆的短半轴长为半径的圆与直线0x y -相切．⑴求椭圆C 的方程；⑵设(4,0)P ，M 、N 是椭圆C 上关于x 轴对称的任意两个不同的点，连结PN 交椭圆C 于另一点E ，求直线PN 的斜率的取值范围；⑶在⑵的条件下，证明直线ME 与x 轴相交于定点． 【解析】 ⑴由题意知c e a ==， 所以22222234c a b e a a -===，即224a b =，又因为1b ==，所以224,1a b ==， 故椭圆C 的方程为C ：2214x y +=．⑵由题意知直线PN 的斜率存在，设直线PN 的方程为(4)y k x =- ① 联立22(4)14y k x x y =-⎧⎪⎨+=⎪⎩消去y 得：2222(41)324(161)0k x k x k --+-=， 由2222(32)4(41)(644)0k k k ∆=-+->得21210k -<，又0k =不合题意，所以直线PN的斜率的取值范围是0k <<或0k << ⑶设点1122(,),(,)N x y E x y ，则11(,)M x y -， 直线ME 的方程为212221()y y y y x x x x +-=--， 令0y =，得221221()y x x x x y y -=-+，将1122(4),(4)y k x y k x =-=-代入整理，得12121224()8x x x x x x x -+=+-． ②由得①2212122232644,4141k k x x x x k k -+==++代入②整理，得1x =， 所以直线ME 与x 轴相交于定点(1,0)．28．（宣武·理·题19）已知椭圆22221(0)x y a b a b+=>>⑴若原点到直线0x y b +-=⑵设过椭圆的右焦点且倾斜角为45︒的直线l 和椭圆交于,A B 两点． i)当||AB b 的值；ii)对于椭圆上任一点M ，若OM OA OB λμ=+，求实数,λμ满足的关系式． 【解析】 ⑴∵d ==2b =．∵c e a ==2223c a =．∵222a b c -=，∴22243a a -=，解得2212,4ab ==．椭圆的方程为221124x y+=．⑵i)∵c a =2222223,23a b c a b ===，椭圆的方程可化为 22233x y b += …………①易知右焦点,0)F ，据题意有AB：y x = ………②由①，②有：22430x b -+= …………③ 设1122(,),(,)A x y B x y ，||AB =∴1b =ii)显然OA 与OB 可作为平面向量的一组基底，由平面向量基本定理，对于这一平面内的向量OM ，有且只有一对实数,λμ，使得等式OM OA OB λμ=+成立．设(,)M x y ，∵1122(,)(,)(,)x y x y x y λμ=+，∴1212,x x x y y y λμλμ=+=+又点M 在椭圆上，∴2221212()3()3x x y y b λμλμ+++= ……………④由③有：2121234b x x x x +==则222212121212121233()()4()63960x x y y x x x x x x x x b b b b +=+=-++=-+=……………⑤又,A B 在椭圆上，故有222222112233,33x y b x y b +=+= …………⑥将⑥，⑤代入④可得：221λμ+=．29．（宣武·文·题19）已知椭圆的中心在原点O ，焦点在x轴上，点(A -是其左顶点，点C 在椭圆上且0,||||AC CO AC CO ⋅==． ⑴求椭圆的方程；⑵若平行于CO 的直线l 和椭圆交于,M N 两个不同点，求CMN △面积的最大值，并求此时直线l 的方程．【解析】 ⑴设椭圆的标准方程为22221(0)x y a b a b+=>>，∵左顶点(,||||A AC CO AC CO -⊥=． ∴212a =，(C又∵C 在椭圆上，∴233112b+=，24b = ∴椭圆的标准方程为221124x y +=．⑵设1122(,),(,)M x y N x y∵CO 的斜率为1-，∴设直线l 的方程为y x m =-+，代入221124x y +=，得22463120x mx m -+-=．22122123644(312)0323124m m m x x m x x ⎧⎪∆=-⋅->⎪⎪+=⎨⎪⎪-⋅=⎪⎩∴||MN ==又C 到直线l的距离d ==，∴CMN △的面积1||2S MN d =⋅⋅=22162m m +-= 当且仅当2216m m =-时取等号，此时m =± ∴直线l的方程为0x y +±=．30．（崇文·理·题19）已知抛物线24y x =，点(1,0)M 关于y 轴的对称点为N ，直线l 过点M 交抛物线于,A B 两点． ⑴证明：直线,NA NB 的斜率互为相反数； ⑵求ANB ∆面积的最小值；⑶当点M 的坐标为(,0)(0m m >，且1)m ≠．根据⑴⑵推测并回答下列问题（不必说明理由）： ①直线,NA NB 的斜率是否互为相反数？ ②ANB △面积的最小值是多少？【解析】 ⑴设直线l 的方程为()1(0)y k x k =-≠．由()21,4,y k x y x ⎧=-⎪⎨=⎪⎩ 可得 ()2222240k x k x k -++=． 设()()1122,,,A x y B x y ，则21212224,1k x x x x k ++==．∴124y y =-∴()1,0N - 1212221212441144NA NB y y y yk k x x y y +=+=+++++ ()()()()()()2212212112222212124444(4444)04444y y y y y y y y y y y y ⎡⎤+++-+-+⎣⎦===++++．又当l 垂直于x 轴时，点,A B 关于x 轴，显然0,NA NB NA NB k k k k +==-． 综上，0,NA NB NA NB k k k k +==-． ---------------- 5分 ⑵12NAB S y y ∆=-==4． 当l 垂直于x 轴时，4NAB S ∆=．∴ANB ∆面积的最小值等于4． ----------------10分 ⑶推测：①NA NB k k =-；②ANB∆面积的最小值为4．31．（崇文·文·题19）已知椭圆()222210x y a b a b+=>>短轴的一个端点(D ，离心率12e =．过D 作直线l 与椭圆交于另一点M ，与x轴交于点A （不同于原点O ），点M 关于x 轴的对称点为N ，直线DN 交x 轴于点B ． ⑴求椭圆的方程； ⑵求OA OB ⋅的值．【解析】⑴由已知，2,a b =所以椭圆方程为 22143x y +=．⑵设直线l 方程为y kx =0y=，得A ⎛⎫⎪ ⎪⎝⎭．由方程组223412y kx x y ⎧=+⎪⎨+=⎪⎩ 可得(223412x k x +=，即()22340k x++=．所以M x =，所以M ⎛ ⎝，N ⎛- ⎝．所以34DN k k ==． 直线DN 的方程为34y x k=令0y =，得B ⎛⎫⎪ ⎪⎝⎭．所以 OA OB ⋅=4=．32．（朝阳·理·题19）已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，且经过点31,2⎛⎫- ⎪⎝⎭，过点()2,1P 的直线l 与椭圆C 在第一象限相切于点M ．⑴求椭圆C 的方程；⑵求直线l 的方程以及点M 的坐标；⑶是否存过点P 的直线1l 与椭圆C 相交于不同的两点,A B ，满足2PA PB PM ⋅=？若存在，求出直线1l 的方程；若不存在，请说明理由．【解析】 ⑴设椭圆C 的方程为22221(0)x y a b a b +=>>，由题意得22222191412a b c a a b c ⎧+=⎪⎪⎪=⎨⎪⎪=+⎪⎩解得224,3a b ==，故椭圆C 的方程为22143x y+=．⑵因为过点()2,1P 的直线l 与椭圆在第一象限相切，所以l 的斜率存在，故可设直线l 的方程为(2)1y k x =-+．由221,43(2)1x y y k x ⎧+=⎪⎨⎪=-+⎩得222(34)8(21)161680k x k k x k k +--+--=． ①因为直线l 与椭圆相切，所以222[8(21)]4(34)(16168)0k k k k k ∆=---+--=．整理，得32(63)0k +>．解得12k >-．所以直线l 的方程为11(2)1222y x x =--+=-+．将12k =-代入①式，可以解得M 点横坐标为1，故切点M 坐标为31,2⎛⎫⎪⎝⎭．⑶若存在直线1l 满足条件的方程为1(2)1y k x =-+，代入椭圆C 的方程得 22211111(34)8(21)161680k x k k x k k +--+--=．因为直线1l 与椭圆C 相交于不同的两点,A B ，设,A B 两点的坐标分别为1122(,),(,)x y x y ， 所以2221[8(21)]4(34)(16168)32(63)0.k k k k k k ∆=---+--=+> 所以12k =-．又21111121222118(21)16168,3434k k k k x x x x k k ---+==++，因为2PA PB PM ⋅=，即12125(2)(2)(1)(1)4x x y y --+--=，所以2212(2)(2)(1)||x x k PM --+=54=．即2121215[2()4](1)4x x x x k -+++=．所以222121111222111161688(21)445[24](1)3434344k k k k k k k k k ---+-⋅++==+++，解得112k =±． 因为,A B 为不同的两点，所以12k =．于是存在直线1l 满足条件，其方程为12y x =．33．（朝阳·文·题19）已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，且经过点31,2M ⎛⎫⎪⎝⎭，过点()2,1P 的直线l 与椭圆C 相交于不同的两点,A B ． ⑴求椭圆C 的方程；⑵是否存直线l ，满足2PA PB PM ⋅=？若存在，求出直线l 的方程；若不存在，请说明理由．【解析】 ⑴设椭圆C 的方程为22221(0)x y a b a b +=>>，由题意得22222191412a b c a a b c ⎧+=⎪⎪⎪=⎨⎪⎪=+⎪⎩解得224,3a b ==，故椭圆C 的方程为22143x y += 5分⑵若存在直线l 满足条件，设直线l 的方程为(2)1y k x =-+由221,43(2)1x y y k x ⎧+=⎪⎨⎪=-+⎩得222(34)8(21)161680k x k k x k k +--+--= 因为直线l 与椭圆C 相交于不同的两点,A B ． 设,A B 两点的坐标分别为()()1122,,,x y x y所以222[8(21)]4(34)(16168)0.k k k k k ∆=---⋅+⋅-->整理，得32(63)0k +>解得12k >-．又21212228(21)16168,3434k k k k x x x x k k ---+==++ 且2PA PB PM ⋅=．即12125(2)(2)(1)(1)4x x y y --+--=． 所以2212(2)(2)(1)||x x k PM --+=54=即212125[2()4](1).4x x x x k -+++=所以222222161688(21)445[24](1)3434344k k k k k k k k k ---+-⋅++==+++ 解得12k =±．所以12k =．于是，存在直线l 满足条件，其方程为12y x =．二模：1、（丰台区）20．（13分）已知抛物线24x y =的焦点为F ，过焦点F 且不平行于x 轴的动直线l 交抛物线于A ，B 两点，抛物线在A 、B 两点处的切线交于点M ． （Ⅰ）求证：A ，M ，B 三点的横坐标成等差数列；（Ⅱ）设直线MF 交该抛物线于C ，D 两点，求四边形ACBD 面积的最小值．解：（Ⅰ）由已知，得(0,1)F ，显然直线AB 的斜率存在且不得0， 则可设直线AB 的方程为1y kx =+（0k ≠），11(,)A x y ，22(,)B x y ，由24,1x y y kx ⎧=⎨=+⎩消去y ，得2440x kx --=，显然216160k ∆=+>. 所以124x x k +=，124x x =-. ………………………………………………2分由24x y =，得214y x =，所以'12y x =， 所以，直线AM 的斜率为112AM k x =，所以，直线AM 的方程为1111()2y y x x x -=-，又2114x y =，所以，直线AM 的方程为 112()x x y y =+①。

2010届北京市海淀区第一学期高三年级期末练习数学试卷（文科）1．225sin =（ ）A ．1B ．—1C ．22D ．—22 2．下面给出四个点中，位于⎩⎨⎧>+-<-+0101y x y x 所表示的平面区域内的点是（ ）A ．（0，2）B ．（—2，0）C ．（0，—2）D ．（2，0） 3．双曲线222=-x y 的渐近线方程是（ ）A ．x y ±=B ．x y 2±=C ．x y 3±=D ．x y 2±=4．某学校准备调查高三年级学生完成课后作业所需时间，采取了两种抽样调查的方式：第一种由学生会的同学随机对24名同学进行调查；第二种由教务处对年级的240名学生编号，由001到240，请学号最后一位为3的同学参加调查，则这两种抽样方式依次为（ ）A ．分层抽样，简单随机抽样B ．简单随机抽样，分层抽样C ．分层抽样，系统抽样D ．简单随机抽样， 系统抽样5．已知n m ,是两条不同直线，βα,是两个不同平面.下列命题中不．正确的是 （ ）A ．若n m n m //,,//则=βααB ．若αα⊥⊥n m n m 则,,//C ．若βαβα//,,则⊥⊥m mD ．若βαβα⊥⊂⊥则,,m m6．如图，向量b a -等于（ ）A ．2142e e --B ．2124e e --C ．213e e -D ．2133e e +7．若直线l 与直线7,1==x y 分别交于点P ，Q ，且线段PQ 的中点坐标为（1，—1），则直线l 的斜率为 （ ）A ．31B ．—31 C ．—23 D ．32 8．已知椭圆C ：1422=+y x 的焦点为F 1，F 2，若点P 在椭圆上，且满足|PO|2=|PF 1|·|PF 2| （其中O 为坐标原点），则称点P 为“★点”.那么下列结论正确的是 （ ）A ．椭圆C 上的所有点都是“★点”B ．椭圆C 上仅有有限个点是“★点” C ．椭圆C 上的所有点都不是“★点”D ．椭圆C 上有无穷多个点（但不是所有的点）是“★点”第Ⅱ卷（共110分）二、填空题:本大题共6小题，每小题5分，共30分.把答案填在题中横线上. 9．抛物线x y 42=的准线方程是____________10．某程序的框图如图所示，则执行该程序，输出的S=11．一个几何体的三视图如图所示，则该几何体的表面积为__________________.12．在区间[—2，2]上，随机地取一个数x ，则2x 位于0到1之间的概率是____________.13．已知F 1为椭圆12:22=+y x C 的左焦点，直线1:-=x y l 椭圆C 交于A 、B 两点，那么|F 1A|的+|F 1B|值为_______.14．对于函数)(x f ，若存在区间M M x x f y y b a b a M =∈=<=}),(|{),(],,[使得，则称区间M 为函数)(x f 的一个“稳定区间”.请你写出一个具有“稳定区间”的函数__________;（只要写出一个即可） 给出下列4个函数：①xe xf =)(；②3)(x x f =，③x x f 2cos)(π= ④1ln )(+=x x f其中存在“稳定区间”的函数有_______（填上正确的序号） 15．（本小题共12分）已知集合}1521|{},052|{+<<+=<-+=a x a x P x x x S （I ）求集合S ；（II ）若P S ⊆，求实数a 的取值范围. 16．（本小题共13分）某校高三年级进行了一次数学测验，随机从甲乙两班各抽取6名同学，所得分数的茎叶图如下图所示：（I ）根据茎叶图判断哪个班的平均分数较高，并说明理由;（II ）现从甲班这6名同学中随机抽取两名同学，求他们的分数之和大于165分的概率.17．（本小题共14分）长方体ABCD —A 1B 1C 1D 1中AB=1，AA 1=AD=2.点E 为AB 中点. （I ）求三棱锥A 1—ADE 的体积； （II ）求证：A 1D ⊥平面ABC 1D 1；（III ）求证：BD 1//平面A 1DE.18．（本小题共13分）函数).(1)(2R a x ax x f ∈++=. （I ）若))1(,1()(f x f 在点处的切线斜率为21，求实数a 的值； （II ）若1)(=x x f 在处取得极值，求函数)(x f 的单调区间. 19．（本小题共14分）已知圆C 经过点)2,0(),0,2(B A -，且圆心在直线x y =上，且，又直线l ：1+=kx y 与圆C 相交于P 、Q 两点. （I ）求圆C 的方程；（II ）若⋅=—2，求实数k 的值；（III ）过点（0，1）作直线l 1与l 垂直，且直线l 1与圆C 交于M 、N 两点，求四边形PMQN面积的最大值.20．（本小题共14分）已知函数.),(,0:}{.,)(*112N n a f a a a R m m x x f n n n ∈==∈+=+如下定义数列其中 （I ）当m=1时，求432,,a a a 的值；（II ）是否存在实数m ，使432,,a a a 构成公差不为0的等差数列？若存在，请求出实数m 的值，若不存在，请说明理由；（III ）求证：当41>m 时，总能找到.2010,>∈k a N k 使得。

海 淀 区 九 年 级 第 二 学 期 期 中 测 评数 学2010.5一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．21-的倒数是 A. 2 B.2- C.21 D.21- 2．2010年2月12日至28日，温哥华冬奥会官方网站的浏览量为275 000 000人次. 将 275 000 000用科学记数法表示为A. 72.7510⨯ B.727.510⨯ C. 82.7510⨯ D.90.27510⨯ 3．右图是某几何体的三视图，则这个几何体是A . 圆柱B . 正方体C . 球D . 圆锥4．一个多边形的内角和是外角和的2倍，则这个多边形的边数为A . 5B .6C . 7D . 85．一个布袋中有4个除颜色外其余都相同的小球，其中3个白球，1个红球．从袋中任意摸出1个球是白球的概率是 A ．43 B ．41 C ．32 D ．31 6． 四名运动员参加了射击预选赛，他们成绩的平均环数x 及其方差2s 如表所示．如果选出一个成绩较好且状态稳定的人去参赛，那么应选A ．甲B ．乙C．丙 D ．丁7．把代数式322363x x y xy-+分解因式，结果正确的是A．(3)(3)x x y x y+-B．223(2)x x xy y-+ C．2(3)x x y+D．23()x x y-8. 如图,点E、F是以线段BC为公共弦的两条圆弧的中点，6BC=. 点A、D分别为线段EF、BC上的动点. 连接AB、AD，设BD x=，22AB AD y-=，下列图象中，能表示y与x的函数关系的图象是A．B．C．D．二、填空题（本题共16分，每小题4分）9．函数13-=xy的自变量x的取值范围是．10．如图, O的半径为2，点A为O上一点，OD⊥弦BC于点D，1OD=,则BAC∠=________︒．11．若代数式26x x b-+可化为2()1x a--，则b a-的值是．12. 如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△211B D C的面积为1S，△322B D C的面积为2S，…，△1n n nB D C+的面积为nS，则2S= ；nS=____ （用含n的式子表示）．三、解答题（本题共30分，每小题5分）130112cos301)()2-︒+-．14．解方程：23233xx x+=-+．15. 如图, △OAB和△C O D均为等腰直角三角形，90AOB COD∠=∠=︒, 连接AC、BD.求证: AC BD=.A16． 已知：2310x x +=，求代数式2(2)(10)5x x x -++-的值.17. 已知：如图，一次函数y x m =+与反比例函数y =的图象在第一象限的交点为(1)A n ，．（1）求m 与n 的值；（2）设一次函数的图像与x 轴交于点B ，连接OA ，求BAO ∠的度数．18. 列方程（组）解应用题：2009年12月联合国气候会议在哥本哈根召开．从某地到哥本哈根，若乘飞机需要3小时，若乘汽车需要9小时．这两种交通工具平均每小时二氧化碳的排放量之和为70千克，飞机全程二氧化碳的排放总量比汽车的多54千克，分别求飞机和汽车平均每小时二氧化碳的排放量．四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分） 19．已知：如图，在直角梯形ABCD 中，AD ∥BC ，︒=∠90DCB ，BD AC ⊥于点O ，4,2==BC DC ，求AD 的长.20. 已知：如图，O 为ABC ∆的外接圆，BC 为O 的直径，作射线BF ，使得BA 平分CBF ∠，过点A 作AD BF ⊥于点D .（1） 求证：DA 为O 的切线；（2） 若1BD =，1tan 2BAD ∠=，求O 的半径. 21. 2009年秋季以来，我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分.图1 图2请根据以上信息解答问题： （1）补全图1和图2；（2）如果全校学生家庭总人数约为3000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量.22．阅读：如图1，在ABC ∆和DEF ∆中，90ABC DEF ∠=∠=︒,,AB DE a ==BC EF b == ()b a <,B 、C 、D 、 E 四点都在直线m 上，点B 与点D 重合.连接AE 、FC ，我们可以借助于ACE S ∆和FCE S ∆的大小关系证明不等式：222a b ab +>（0b a >>）.证明过程如下:∵,,.BC b BE a EC b a ===-∴11(),22ACE S EC AB b a a ∆=⋅=- 11().22FCE S EC FE b a b ∆=⋅=-∵0b a >>,∴FCE S ACE S ∆∆>. 即a ab b a b )(21)(21->-. ∴22b ab ab a ->-. ∴222a b ab +>. 解决下列问题：（1）现将△DEF 沿直线m 向右平移，设()BD k b a =-,E图1F图2且01k ≤≤.如图2,当BD EC =时, k = .利用此图,仿照上述方法,证明不等式：222a b ab +>（0b a >>）.（2）用四个与ABC ∆全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式.请你画出一个．．示意图，并简要说明理由.五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．关于x 的一元二次方程240x x c -+=有实数根，且c 为正整数. （1）求c 的值；（2）若此方程的两根均为整数，在平面直角坐标系xOy 中,抛物线24y x x c =-+与x 轴交于A 、B 两点（A 在B 左侧），与y 轴交于点C . 点P 为对称轴上一点，且四边形OBPC 为直角梯形，求PC 的长；（3）将（2）中得到的抛物线沿水平方向平移，设顶点D 的坐标为(),m n ,当抛物线与（2）中的直角梯形OBPC 只有两个交点，且一个交点在PC 边上时，直接写出m 的取值范围.24. 点P 为抛物线222y x mx m =-+(m 为常数，0m >)上任一点，将抛物线绕顶点G 逆时针旋转90︒后得到的新图象与y 轴交于A 、B 两点（点A 在点B 的上方），点Q 为点P 旋转后的对应点.（1）当2m =，点P 横坐标为4时，求Q 点的坐标； （2）设点(,)Q a b ，用含m 、b 的代数式表示a ； （3) 如图，点Q 在第一象限内, 点D 在x 轴的正半轴上，点C为OD 的中点，QO 平分AQC ∠，2AQ QC =，当QD m =时，求m 的值.25.已知：AOB △中，2AB OB ==，COD △中，3CD OC ==,ABO DCO =∠∠. 连接AD 、BC ，点M 、N 、P 分别为OA 、OD 、BC 的中点.图1 图2(1) 如图1，若A 、O 、C 三点在同一直线上，且60ABO =∠，则PMN △的形状是________________，此时ADBC=________； (2) 如图2，若A 、O 、C 三点在同一直线上，且2ABO α=∠，证明PMN BAO △∽△，并计算ADBC的值（用含α的式子表示）； (3) 在图2中，固定AOB △，将COD △绕点O 旋转，直接写出PM 的最大值.海淀区九年级第二学期期中测评数学试卷答案及评分参考一、选择题（本题共32分，每小题4分）二、填空题（本题共16分，每小题4分）三、解答题（本题共30分，每小题5分） 130112cos301)()2-︒+-.解： 原式=212+-----------------------------------4分 1.---------------------------------5分 14．解方程：23233x x x +=-+. 解：去分母，得 22(3)3(3)2(9)x x x x ++-=-． ---------------------------------1分去括号，得222639218x x x x ++-=-． ---------------------------------2分 解得 1x =-． ---------------------------------4分 经检验，1x =-是原方程的解．∴ 原方程的解是1x =-． ---------------------------------5分 15．证明：∵ 90,AOB COD ∠=∠=︒∴ .AOC BOD ∠=∠---------------------------------1分 ∵ △OAB 与△COD 均为等腰三角形，∴ ,.OA OB OC OD ==---------------------------------3分 在△AOC 和△BOD 中，,,,AO BO AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴ △AOC ≌△BOD .---------------------------------4分 ∴ AC BD =.---------------------------------5分16．解： 原式=5104422-+++-x x x x ---------------------------------2分 =1622-+x x .---------------------------------3分 当2310x x +=时，原式=1)3(22-+x x ---------------------------------4分 191102=-⨯=.---------------------------------5分17．解：（1）∵点(1,)A n 在双曲线y =上，∴n =分又∵(1A 在直线y m =+上，∴ m =.---------------------------------2分 （2）过点A 作AM ⊥x 轴于点M . ∵ 直线33233+=x y 与x 轴交于点B ，∴033x +=.解得 2x =-.∴ 点B 的坐标为-20（，）.∴ 2=OB .---------------------------------3分∵点A 的坐标为， ∴1,3==OM AM .在Rt △AOM 中，︒=∠90AMO , ∴tan 3==∠OMAMAOM . ∴︒=∠60AOM .---------------------------------4分由勾股定理，得 2=OA . ∴.OA OB = ∴BAO OBA ∠=∠. ∴︒=∠=∠3021AOM BAO .---------------------------------5分 18．解：设乘飞机和坐汽车每小时的二氧化碳排放量分别是x 千克和y 千克. ………1分依题意，得70,3954.x y x y +=⎧⎨-=⎩---------------------------------2分解得57,13.x y =⎧⎨=⎩----------------------------4分答: 飞机和汽车每小时的二氧化碳排放量分别是57千克和13千克. ………5分 四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分） 19．解法一：过点D 作//DE AC 交BC 的延长线于点E .---------------------------------1分∴ BDE BOC ∠=∠. ∵ AC BD ⊥于点O , ∴ 90BOC ∠=︒.∴ 90BDE ∠=︒. ---------------2分 ∵ //AD BC ，∴ 四边形ACED 为平行四边形. ---------------3分 ∴ AD CE =.∵ 90,90BDE DCB ∠=︒∠=︒，∴ 2DC BC CE =⋅.-------------------------------4分 ∵ 2,4DC BC ==， ∴ 1CE =.∴ 1AD =.---------------------------------5分 解法二： //AD BC ，∴ 180ADC DCB ∠+∠= .又 90DCB ∠=，∴ 90ADC ∠= . --------------------------------------------1分AC BD ⊥于点O , ∴ 90BOC ∠= .∴ 90DBC ACB ∠+∠= . 90ACB ACD ∠+∠= .∴ DBC ACD ∠=∠.------------------------------------------2分∴ ACD DBC ∠=∠tan tan .---------------------------------------------3分在Rt △BCD 中，tan CDDBC BC ∠=.在Rt △ACD 中，tan ADACD CD∠=.∴CD ADBC CD=.------------------------------------------4分 4BC =,2CD =，∴ 1AD =. ---------------------------------------------5分20. （1）证明：连接AO . ---------------------------------1分∵ AO BO =，∴ 23∠=∠. ∵ BA CBF ∠平分， ∴ 12∠=∠. ∴ 31∠=∠ .∴ DB ∥AO .--------------------------2分 ∵ AD DB ⊥, ∴ 90BDA ∠=︒. ∴ 90DAO ∠=︒. ∵ AO 是⊙O 半径，∴ DA 为⊙O 的切线. ---------------------------------3分 （2） ∵ AD DB ⊥,1BD =，1tan 2BAD ∠=， ∴ 2AD =.由勾股定理，得AB = --------------------------------4分∴sin 45∠=.∵ BC 是⊙O 直径， ∴ ︒=∠90BAC . ∴ 290C ∠+∠=︒.又∵ 4190∠+∠=︒, 21∠=∠, ∴ 4C ∠=∠. 在Rt △ABC 中，sin AB BC C ==sin 4AB∠=5. ∴ O 的半径为52.-------------------------5分 21. 解：(1)50-------------------------2分--------------------------4分(2) 全体学生家庭月人均用水量为1505164323502421103000⨯+⨯+⨯+⨯+⨯⨯--------------------------5分9040=（吨）.答：全校学生家庭月用水量约为 9040吨.--------------------------6分22．（1）12k =；--------------------------1分 证明：连接AD 、BF .可得1()2BD b a =-.∴ ()()11112224ABD S BD AB b a a a b a ∆=⋅=⨯⨯-⋅=-， ()()11112224FBD S BD FE b a b b b a ∆=⋅=⨯⨯-⋅=-.∵ 0>>a b ，∴ FBD ABD S S ∆∆<， 即()14a b a -()14b b a <-. ∴ ab b a ab -<-22.∴ ab b a 222>+.--------------------------2分 （2）答案不唯一，图1分，理由1分. 举例：如图，理由： 延长BA 、FE 交于点I . ∵ 0>>a b ，∴ IBCE ABCD S S >矩形矩形， 即 )()(a b a a b b ->-. ∴ 22a ab ab b ->-.∴ ab b a 222>+.--------------------------4分 举例：如图，理由：四个直角三角形的面积和11422S a b ab =⨯⋅=， 大正方形的面积222S a b =+. ∵ 0>>a b ， ∴ 21S S >.∴ ab b a 222>+.--------------------------4分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．解：（1）∵关于x 的一元二次方程240x x c -+=有实数根，∴ △=0416≥-c .∴ .4≤c -----------------------1分 又∵ c 为正整数，∴ 4,3,2,1=c . ------------------- 2分 （2）∵ 方程两根均为整数，∴ 4,3=c .---------------3分又∵ 抛物线与x 轴交于A 、B 两点， ∴ 3=c .∴ 抛物线的解析式为243y x x =-+.--------------4分∴ 抛物线的对称轴为2x =.∵ 四边形OBPC 为直角梯形，且90COB ∠=︒， ∴ PC ∥BO .∵ P 点在对称轴上，∴ 2=PC .--------------5分（3）02≤<-m 或42≤<m .----------- 7分（写对一个给1分）24. 解：（1）当m =2时，2)2(-=x y ，则(2,0)G ，(4,4)P . --------------------1分如图，连接QG 、PG ,过点Q 作QF x ⊥轴于F ,过点P 作PE x ⊥轴于E . 依题意,可得△GQF ≌△PGE .则2,4,FQ EG FG EP ==== ∴ 2=FO .∴ ()2,2-Q . ------------------2分（2）用含,m b 的代数式表示a ：2b m a -=. ------4分 （3）如图，延长QC 到点E ，使CQ CE =,连接OE . ∵ C 为OD 中点,∴ CD OC =. ∵ QCD ECO ∠=∠, ∴ △ECO ≌△QCD .∴ m DQ OE ==. ------------------5分 ∵ QC AQ 2=, ∴ QE AQ =. ∵ QO 平分AQC ∠, ∴ 21∠=∠.∴ △AQO ≌△EQO . ------------------6分∴ m EO AO ==.∴ ()m A ,0.------------------7分 ∵ ()m A ,0在新的图象上, ∴ 20m m -=.∴ 11=m ，02=m （舍）.∴ 1m =. ------------------8分25. 解：(1)等边三角形，1；(每空1分) ------------------------2分（2）证明：连接BM 、CN .由题意，得BM OA ⊥，CN OD ⊥,α-︒=∠=∠90COD AOB . ∵ A 、O 、C 三点在同一直线上， ∴ B 、O 、D 三点在同一直线上.∴ 90BMC CNB ==∠∠. ∵ P 为BC 中点，∴ 在Rt △BMC 中，BC PM 21=.在Rt △BNC 中，BC PN 21=.∴ PN PM =.---------------------------3分∴ B 、C 、N 、M 四点都在以P 为圆心，12BC 为半径的圆上. ∴ 2MPN MBN =∠∠.又∵ α=∠=∠ABO MBN 21， ∴ MPN ABO =∠∠.∴ PMN BAO △∽△. ----------------------------------4分∴ BAAOPM MN =. 由题意，12MN AD =，又BC PM 21=.∴ PM MNBC AD =.------------------------------------5分 ∴ AD AOBC BA=. 在Rt BMA △中，αsin =ABAM. ∵ AM AO 2=，∴2sin AOBAα=.∴αsin 2=BC AD.------------------------------6分 （3）52.--------------------------------7分(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。

海淀区高三年级第二学期期中练习数 学 （理科） 2010.4第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1．在复平面内，复数1iiz =-（i 是虚数单位）对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．在同一坐标系中画出函数log a y x =，x y a =，y x a =+的图象，可能正确的是（ ）3．在四边形ABCD 中，AB DC =，且AC ·BD ＝0，则四边形ABCD 是（ ）A.矩形B. 菱形C. 直角梯形D. 等腰梯形4．在平面直角坐标系xOy 中，点P 的直角坐标为(1,.若以原点O 为极点，x 轴正半轴为极轴建立极坐标系，则点P 的极坐标可以是 （ ）A ．1,3π⎛⎫- ⎪⎝⎭B ．42,3π⎛⎫ ⎪⎝⎭C ．2,3π⎛⎫- ⎪⎝⎭D ．42,3π⎛⎫-⎪⎝⎭5．一个体积为的正三棱柱的三视图如图所示， 则这个三棱柱的左视图的面积为 （ ） A ． B ．8C ．D ．126．已知等差数列1,,a b ，等比数列3,2,5a b ++，则该等差数列的公差为（ ）A ．3或3-B ．3或1-C ．3D ．3-7．已知某程序框图如图所示，则执行该程序后输出的结果是( )A ．1-B ．1B AC DC ．2D ．128．已知数列()1212:,,,0,3nn A a a a a a a n ≤<<<≥具有性质P ：对任意(),1i j i j n ≤≤≤，j i a a +与j i a a -两数中至少有一个是该数列中的一项. 现给出以下四个命题：①数列0,1,3具有性质P ；②数列0,2,4,6具有性质P ； ③若数列A 具有性质P ，则10a =；④若数列()123123,,0a a a a a a ≤<<具有性质P ，则1322a a a +=. 其中真命题有（ ） A ．4个 B ．3个C ．2个D ．1个第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.9.某校为了解高三同学寒假期间学习情况，抽查了100名同学，统计他们每天平均学习时间,绘成频率分布直方图（如图）.则这100名同学中学习时间在6~8小时内的人数为 _______.10．如图，AB 为O 的直径，且8AB = ，P 为OA 的中点，过P 作O 的弦CD ，且:3:4CP PD =，则弦CD 的长度为 . 11．给定下列四个命题：①“6x π=”是“1sin 2x =”的充分不必要条件； ②若“p q ∨”为真，则“p q ∧”为真；xB③若a b <，则22am bm <； ④若集合A B A =，则A B ⊆.其中为真命题的是 （填上所有正确命题的序号）.12．在二项式25()ax x -的展开式中，x 的系数是10-，则实数a 的值为 .13．已知有公共焦点的椭圆与双曲线中心为原点，焦点在x 轴上，左右焦点分别为12,F F ，且它们在第一象限的交点为P ，12PF F ∆是以1PF 为底边的等腰三角形.若110PF =，双曲线的离心率的取值范围为(1,2).则该椭圆的离心率的取值范围是 .14．在平面直角坐标系中，点集22{(,)|1}A x y x y =+≤，{(,)|4,0,,340}B x y x y x y =≤≥-≥， 则（1）点集1111{(,)3,1,(,)}P x y x x y y x y A ==+=+∈所表示的区域的面积为_____； （2）点集12121122{(,),,(,),(,)}Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为 .三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．（本小题满分13分）已知函数()sin()(0,||)f x x ωϕωϕπ=+><的图象如图所示. （Ⅰ）求,ωϕ的值；（Ⅱ）设()()()4g x f x f x π=-，求函数()g x 的单调递增区间.16．（本小题满分13分）某商场为吸引顾客消费推出一项优惠活动.活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置. 若指针停在A 区域返券60元；停在B 区域返券30元；停在C 区域不返券. 例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和.（Ⅰ）若某位顾客消费128元，求返券金额不低于30元的概率；（Ⅱ）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X （元）.求随机变量X 的分布列和数学期望. 17．（本小题满分14分）如图，三棱柱111ABC A B C -中，侧面11AA C C ⊥底面ABC ，112,AA AC AC AB BC ====, 且AB BC ⊥,O 为AC 中点. （Ⅰ）证明：1A O ⊥平面ABC ；（Ⅱ）求直线1A C 与平面1A AB 所成角的正弦值；（Ⅲ）在1BC 上是否存在一点E ，使得//OE 平面1A AB ，若不存在，说明理由；若存在，确定点E 的位置.18．（本小题满分13分）已知函数()ln ,f x x a x =+其中a 为常数，且1a ≤-.（Ⅰ）当1a =-时，求()f x 在2[e,e ]（e=2.718 28…）上的值域； （Ⅱ）若()e 1f x ≤-对任意2[e,e ]x ∈恒成立,求实数a 的取值范围.1A BCO A 1B 1C19．（本小题满分13分）已知椭圆C 的中心在原点，焦点在x 轴上，左右焦点分别为12,F F ，且12||2F F =，点（1，32） 在椭圆C 上.（Ⅰ）求椭圆C 的方程；（Ⅱ）过1F 的直线l 与椭圆C 相交于,A B 两点，且2AF B ∆2F 为圆心且与直线l 相切的圆的方程.20．（本小题满分14分）已知数列{}n a 满足：10a =，21221,,12,,2n n n n a n n a a -+⎧⎪⎪=⎨++⎪⎪⎩为偶数为奇数，2,3,4,.n =（Ⅰ）求567,,a a a 的值； （Ⅱ）设212n n na b -=，试求数列{}n b 的通项公式；（Ⅲ）对于任意的正整数n ，试讨论n a 与1n a +的大小关系.海淀区高三年级第二学期期中练习数 学 （理）参考答案及评分标准 2010．4说明： 合理答案均可酌情给分，但不得超过原题分数.第Ⅰ卷（选择题 共40分）一、选择题（本大题共8小题,每小题5分,共40分）第Ⅱ卷（非选择题 共110分）二、填空题（本大题共6小题,每小题5分, 有两空的小题，第一空3分，第二空2分，共30分）9．30 10．7 11．①，④ 12．1 13．12(,)35 14．π；18π+.三、解答题(本大题共6小题,共80分) 15．（本小题满分13分） 解：（Ⅰ）由图可知πππ=-=)42(4T ,22==Tπω， ………………2分又由1)2(=πf 得，1)sin(=+ϕπ，又(0)1f =-，得sin 1ϕ=-πϕ<||2πϕ-=∴， ………………4分（Ⅱ）由（Ⅰ）知：x x x f 2cos )22sin()(-=-=π………………6分因为()(cos 2)[cos(2)]cos 2sin 22g x x x x x π=---=1sin 42x = ………………9分 所以，24222k x k ππππ-≤≤+，即 (Z)2828k k x k ππππ-≤≤+∈.……………12分故函数()g x 的单调增区间为[,] (Z)2828k k k ππππ-+∈.……………13分 16．（本小题满分13分）解：设指针落在A ,B ,C 区域分别记为事件A ,B ,C .则111(),(),()632P A P B P C ===. ………………3分（Ⅰ）若返券金额不低于30元，则指针落在A 或B 区域.111()()632P P A P B ∴=+=+=………………6分即消费128元的顾客，返券金额不低于30元的概率是12. （Ⅱ）由题意得，该顾客可转动转盘2次.随机变量X 的可能值为0，30，60，90，120.………………7分111(0);224111(30)2;23311115(60)2;263318111(90)2;369111(120).6636P X P X P X P X P X ==⨯===⨯⨯===⨯⨯+⨯===⨯⨯===⨯= ………………10分………………12分其数学期望115110306090120404318936EX =⨯+⨯+⨯+⨯+⨯= .………13分 17． （本小题满分14分）解：（Ⅰ）证明：因为11A A AC =，且O 为AC 的中点， 所以1AO AC ⊥.………………1分又由题意可知，平面11AAC C ⊥平面ABC ，交线为AC ，且1A O ⊂平面11AA C C ， 所以1A O ⊥平面ABC .………………4分（Ⅱ）如图，以O 为原点，1,,OB OC OA 所在直线分别为x ，y ，z 轴建立空间直角坐标系. 由题意可知，112,A A AC AC ===又,AB BC AB BC =⊥1,1,2OB AC ∴== 所以得:11(0,0,0),(0,1,0),(0,1,0),(1,0,0)O A A C C B - 则有：11(0,1,3),(0,1,3),(1,1,0).A C AA AB =-==………………6分设平面1AA B 的一个法向量为(,,)x y z =n ，则有110000AA y x y AB ⎧⎧⋅=+=⎪⎪⇔⎨⎨+=⎪⋅=⎪⎩⎩n n ，令1y =，得1,x z =-=所以(1,1,=-n . ………………7分 11121cos ,|||A C A C A C ⋅<>==n n |n ………………9分因为直线1A C 与平面1A AB 所成角θ和向量n 与1A C 所成锐角互余，所以sin θ=………………10分 （Ⅲ）设0001(,,),,E x y z BE BC λ==………………11分即000(1,,)(x y z λ-=-，得00012x y z λλ⎧=-⎪=⎨⎪=⎩所以(1,2),E λλ=-得(1,2),OE λλ=- ………………12分 令//OE 平面1A AB ，得=0OE ⋅n ，………………13分即120,λλλ-++-=得1,2λ=即存在这样的点E ，E 为1BC 的中点.………………14分18.（本小题满分13分） 解：（Ⅰ）当1a =-时，()ln ,f x x x =-得1()1,f x x '=-………………2分令()0f x '>，即110x->，解得1x >，所以函数()f x 在(1,)+∞上为增函数， 据此，函数()f x 在2[e,e ]上为增函数，………………4分而(e)e 1f =-，22(e )e 2f =-，所以函数()f x 在2[e,e ]上的值域为2[e 1,e 2]--………………6分（Ⅱ）由()1,a f x x '=+令()0f x '=，得10,ax+=即,x a =-当(0,)x a ∈-时，()0f x '<，函数()f x 在(0,)a -上单调递减；当(,)x a ∈-+∞时，()0f x '>，函数()f x 在(,)a -+∞上单调递增； ……………7分 若1e a ≤-≤，即e 1a -≤≤-，易得函数()f x 在2[e,e ]上为增函数，此时，2max ()(e )f x f =，要使()e 1f x ≤-对2[e,e ]x ∈恒成立，只需2(e )e 1f ≤-即可，所以有2e 2e 1a +≤-，即2e e 12a -+-≤而22e e 1(e 3e 1)(e)022-+---+--=<，即2e e 1e 2-+-<-，所以此时无解.………………8分若2e e a <-<，即2e e a ->>-，易知函数()f x 在[e,]a -上为减函数，在2[,e ]a -上为增函数， 要使()e 1f x ≤-对2[e,e ]x ∈恒成立，只需2(e)e 1(e )e 1f f ≤-⎧⎨≤-⎩，即21e e 12a a ≤-⎧⎪⎨-+-≤⎪⎩， 由22e e 1e e 1(1)022-+--++--=<和222e e 1e e 1(e )022-+-+---=>得22e e 1e 2a -+--<≤.………………10分若2e a -≥，即2e a ≤-，易得函数()f x 在2[e,e ]上为减函数，此时，max ()(e)f x f =，要使()e 1f x ≤-对2[e,e ]x ∈恒成立，只需(e)e 1f ≤-即可， 所以有e e 1a +≤-，即1a ≤-，又因为2e a ≤-，所以2e a ≤-.……………12分 综合上述，实数a 的取值范围是2e e 1(,]2-+--∞.……………13分19．（本小题满分13分）解：（Ⅰ）设椭圆的方程为22221,(0)x y a b a b+=>>，由题意可得：椭圆C 两焦点坐标分别为1(1,0)F -，2(1,0)F ..……………1分532422a ∴==+=..……………3分2,a ∴=又1c = 2413b =-=，……………4分故椭圆的方程为22143x y +=. .……………5分（Ⅱ）当直线l x ⊥轴，计算得到：33(1,),(1,)22A B ---，21211||||32322AF B S AB F F ∆=⋅⋅=⨯⨯=，不符合题意..……………6分当直线l 与x 轴不垂直时，设直线l 的方程为：(1)y k x =+，由22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，消去y 得 2222(34)84120k x k x k +++-=， .……………7分显然0∆>成立，设1122(,),(,)A x y B x y ，则221212228412,,3434k k x x x x k k-+=-⋅=++ .……………8分又||AB ==即22212(1)||3434k AB k k +==++， .……………9分 又圆2F的半径r ==.……………10分所以2221112(1)||2234AF Bk S AB r k ∆+==⨯==+ 化简，得4217180k k +-=，即22(1)(1718)0k k -+=，解得1k =±所以，r ==.……………12分故圆2F 的方程为：22(1)2x y -+=. .……………13分（Ⅱ）另解：设直线l 的方程为 1x ty =-，由221143x ty x y =-⎧⎪⎨+=⎪⎩，消去x 得 22(43)690t y ty +--=，0∆>恒成立，设1122(,),(,)A x y B x y ，则12122269,,4343t y y y y t t+=⋅=-++ ……………8分所以12||y y -==243t =+.……………9分又圆2F的半径为r ==，.……………10分所以21212121||||||27AF BS F F y y y y ∆=⋅⋅-=-==，解得21t =，所以r ==……………12分故圆2F 的方程为：22(1)2x y -+=. .……………13分20．（本小题满分14分）解：（Ⅰ）∵ 10a =，21121a a =+=，31222a a =+=，42123a a =+=， ∴ 52325a a =+=；63125a a =+=；73428a a =+=. ………………3分 （Ⅱ）由题设，对于任意的正整数n ，都有：12121111221222n n n n n n n a a b b +--++++===+， ∴ 112n n b b +-=.∴ 数列{}n b 是以1211102a b -==为首项，12为公差的等差数列.∴ 12n n b -=. …………………………………………………………7分 （Ⅲ）对于任意的正整数k ， 当2n k =或1,3n =时，1n n a a +<； 当41n k =+时，1n n a a +=；当43n k =+时，1n n a a +>. ……………………………………8分 证明如下：首先，由12340,1,2,3a a a a ====可知1,3n =时，1n n a a +<； 其次，对于任意的正整数k ，2n k =时，()()122112120n n k k k k a a a a a k a k ++-=-=+-++=-<；…………………9分41n k =+时，14142n n k k a a a a +++-=-()()()()2212212121222222122120k k k k k k k a a k a a k a k a ++=++-+=+-=++-++=所以，1n n a a +=.…………………10分43n k =+时，14344n n k k a a a a +++-=-()()()()()21222122112221221222121221241k k k k k k k k k a a k a a k k a a k a a ++++++=++-+=++-=++++-+=+-+事实上，我们可以证明：对于任意正整数k ，1k k k a a ++≥（*）（证明见后），所以，此时，1n n a a +>. 综上可知：结论得证.…………………12分对于任意正整数k ，1k k k a a ++≥（*）的证明如下： 1）当2k m =（*m ∈N ）时，()()12212212120k k m m m m k a a m a a m a m a m +++-=+-=++-++=>， 满足（＊）式。

海淀区高三年级第二学期期中练习数 学 （理）参考答案及评分标准 2010．4说明： 合理答案均可酌情给分，但不得超过原题分数.第Ⅰ卷（选择题 共40分）一、选择题（本大题共8小题,每小题5分,共40分）第Ⅱ卷（非选择题 共110分）二、填空题（本大题共6小题,每小题5分, 有两空的小题，第一空3分，第二空2分，共30分）9．30 10．7 11．①，④ 12．1 13．12(,)35 14．π；18π+.三、解答题(本大题共6小题,共80分) 15．（本小题满分13分） 解：（Ⅰ）由图可知πππ=-=)42(4T ,22==Tπω， ………………2分又由1)2(=πf 得，1)sin(=+ϕπ，又(0)1f =-，得sin 1ϕ=-πϕ<||2πϕ-=∴， ………………4分（Ⅱ）由（Ⅰ）知：x x x f 2cos )22sin()(-=-=π………………6分因为()(cos 2)[cos(2)]cos 2sin 22g x x x x x π=---=1sin 42x =………………9分 所以，24222k x k ππππ-≤≤+，即(Z)2828k k x k ππππ-≤≤+∈.……………12分 故函数()g x 的单调增区间为[,] (Z)2828k k k ππππ-+∈.……………13分16．（本小题满分13分）解：设指针落在A ,B ,C 区域分别记为事件A ,B ,C .则111(),(),()632P A P B P C ===. ………………3分（Ⅰ）若返券金额不低于30元，则指针落在A 或B 区域.111()()632P P A P B ∴=+=+=………………6分即消费128元的顾客，返券金额不低于30元的概率是12.（Ⅱ）由题意得，该顾客可转动转盘2次.随机变量X的可能值为0，30，60，90，120. ………………7分111(0);224111(30)2;23311115(60)2;263318111(90)2;369111(120).6636P XP XP XP XP X==⨯===⨯⨯===⨯⨯+⨯===⨯⨯===⨯=………………10分………………12分其数学期望115110306090120404318936EX=⨯+⨯+⨯+⨯+⨯=.………13分17．（本小题满分14分）解：（Ⅰ）证明：因为11A A AC=，且O为AC的中点，所以1AO AC⊥. ………………1分又由题意可知，平面11AA C C⊥平面ABC，交线为AC，且1AO⊂平面11AA C C，所以1AO⊥平面ABC. ………………4分（Ⅱ）如图，以O为原点，1,,OB OC OA所在直线分别为x，y，z轴建立空间直角坐标系.由题意可知，112,A A AC AC===又,AB BC AB BC=⊥1,1,2OB AC∴==所以得:11(0,0,0),(0,1,0),(0,1,0),(1,0,0)O A A C C B-则有：11(0,1,(0,1(1,1,0).AC AA AB===………………6分设平面1AA B的一个法向量为(,,)x y z=n，则有110000AA y x y AB ⎧⎧⋅==⎪⎪⇔⎨⎨+=⎪⋅=⎪⎩⎩n n ，令1y =，得1,x z =-=所以(1,1,=-n . ………………7分111cos ,|||A C A C A C ⋅<>==n n |n ………………9分因为直线1A C 与平面1A AB 所成角θ和向量n 与1A C所成锐角互余，所以sin θ=………………10分 （Ⅲ）设0001(,,),,E x y z BE BC λ==………………11分即000(1,,)(1x y z λ-=-，得00012x y z λλ⎧=-⎪=⎨⎪=⎩所以(1,2),E λλ=-得(1,2),OE λλ=-………………12分 令//OE 平面1A AB ，得=0OE ⋅n ，………………13分即120,λλλ-++-=得1,2λ=即存在这样的点E ，E 为1BC 的中点.………………14分18.（本小题满分13分） 解：（Ⅰ）当1a =-时，()ln ,f x x x =-得1()1,f x x '=-………………2分令()0f x '>，即110x->，解得1x >，所以函数()f x 在(1,)+∞上为增函数， 据此，函数()f x 在2[e,e ]上为增函数，………………4分而(e)e 1f =-，22(e )e 2f =-，所以函数()f x 在2[e,e ]上的值域为2[e 1,e 2]--………………6分（Ⅱ）由()1,a f x x '=+令()0f x '=，得10,ax+=即,x a =-当(0,)x a ∈-时，()0f x '<，函数()f x 在(0,)a -上单调递减；当(,)x a ∈-+∞时，()0f x '>，函数()f x 在(,)a -+∞上单调递增； ……………7分 若1e a ≤-≤，即e 1a -≤≤-，易得函数()f x 在2[e,e ]上为增函数，此时，2max ()(e )f x f =，要使()e 1f x ≤-对2[e,e ]x ∈恒成立，只需2(e )e 1f ≤-即可，所以有2e 2e 1a +≤-，即2e e 12a -+-≤而22e e 1(e 3e 1)(e)022-+---+--=<，即2e e 1e 2-+-<-，所以此时无解.………………8分若2e e a <-<，即2e e a ->>-，易知函数()f x 在[e,]a -上为减函数，在2[,e ]a -上为增函数， 要使()e 1f x ≤-对2[e,e ]x ∈恒成立，只需2(e)e 1(e )e 1f f ≤-⎧⎨≤-⎩，即21e e 12a a ≤-⎧⎪⎨-+-≤⎪⎩， 由22e e 1e e 1(1)022-+--++--=<和222e e 1e e 1(e )022-+-+---=>得22e e 1e 2a -+--<≤.………………10分若2e a -≥，即2e a ≤-，易得函数()f x 在2[e,e ]上为减函数，此时，max ()(e)f x f =，要使()e 1f x ≤-对2[e,e ]x ∈恒成立，只需(e)e 1f ≤-即可， 所以有e e 1a +≤-，即1a ≤-，又因为2e a ≤-，所以2e a ≤-.……………12分 综合上述，实数a 的取值范围是2e e 1(,]2-+--∞.……………13分19．（本小题满分13分）解：（Ⅰ）设椭圆的方程为22221,(0)x y a b a b+=>>，由题意可得：椭圆C 两焦点坐标分别为1(1,0)F -，2(1,0)F ..……………1分532422a ∴=+=..……………3分2,a ∴=又1c = 2413b =-=，……………4分故椭圆的方程为22143x y +=. .……………5分（Ⅱ）当直线l x ⊥轴，计算得到：33(1,),(1,)22A B ---，21211||||32322AF B S AB F F ∆=⋅⋅=⨯⨯=，不符合题意..……………6分当直线l 与x 轴不垂直时，设直线l 的方程为：(1)y k x =+，由22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，消去y 得 2222(34)84120k x k x k +++-=， .……………7分 显然0∆>成立，设1122(,),(,)A x y B x y ，则221212228412,,3434k k x x x x k k-+=-⋅=++ .……………8分又||AB ==即2212(1)||34k AB k +==+， .……………9分 又圆2F的半径r ==.……………10分所以22221112(1)12|||2234347AF Bk k S AB r k k ∆+==⨯==++ 化简，得4217180k k +-=，即22(1)(1718)0k k -+=，解得1k =±所以，r ==.……………12分故圆2F 的方程为：22(1)2x y -+=. .……………13分（Ⅱ）另解：设直线l 的方程为 1x ty =-，由221143x ty x y =-⎧⎪⎨+=⎪⎩，消去x 得 22(43)690t y ty +--=，0∆>恒成立，设1122(,),(,)A x y B x y ，则12122269,,4343t y y y y t t+=⋅=-++ ……………8分所以12||y y -===.……………9分又圆2F的半径为r ==，.……………10分所以212121221||||||2437AF BS F F y y y y t ∆=⋅⋅-=-==+，解得21t =，所以r ==……………12分故圆2F 的方程为：22(1)2x y -+=. .……………13分20．（本小题满分14分）解：（Ⅰ）∵ 10a =，21121a a =+=，31222a a =+=，42123a a =+=， ∴ 52325a a =+=；63125a a =+=；73428a a =+=. ………………3分 （Ⅱ）由题设，对于任意的正整数n ，都有：12121111221222n n n n n n n a a b b +--++++===+， ∴ 112n n b b +-=.∴ 数列{}n b 是以1211102a b -==为首项，12为公差的等差数列. ∴ 12n n b -=. …………………………………………………………7分 （Ⅲ）对于任意的正整数k ，当2n k =或1,3n =时，1n n a a +<； 当41n k =+时，1n n a a +=；当43n k =+时，1n n a a +>. ……………………………………8分 证明如下：首先，由12340,1,2,3a a a a ====可知1,3n =时，1n n a a +<； 其次，对于任意的正整数k ，2n k =时，()()122112120n n k k k k a a a a a k a k ++-=-=+-++=-<；…………………9分41n k =+时，14142n n k k a a a a +++-=-()()()()2212212121222222122120k k k k k k k a a k a a k a k a ++=++-+=+-=++-++=所以，1n n a a +=.…………………10分43n k =+时，14344n n k k a a a a +++-=-()()()()()21222122112221221222121221241k k k k k k k k k a a k a a k k a a k a a ++++++=++-+=++-=++++-+=+-+事实上，我们可以证明：对于任意正整数k ，1k k k a a ++≥（*）（证明见后），所以，此时，1n n a a +>. 综上可知：结论得证.…………………12分对于任意正整数k ，1k k k a a ++≥（*）的证明如下： 1）当2k m =（*m ∈N ）时，()()12212212120k k m m m m k a a m a a m a m a m +++-=+-=++-++=>， 满足（＊）式。

海淀区高三年级第二学期期中练习数 学（文）参考答案及评分标准 2010．4说明： 合理答案均可酌情给分，但不得超过原题分数.第Ⅰ卷 （选择题 共40分）一、选择题（本大题共8小题,每小题5分,共40分）第II 券（非选择题 共110分）二、填空题（本大题共6小题,每小题5分, 有两空的小题，第一空3分，第二空2分，共30分）9.4 10.x y 82= 11.6 12.30 13.1214.π，π+12 15.（本小题满分13分） 解：（I ）由图可知，A=1 …………1分,24π=T 所以π2=T ……………2分 所以1=ω ……………3分又1)4sin()4(=+=ϕππf ，且22ππϕ-<<所以4πϕ=……………5分所以)4sin()(π+=x x f . ……………6分（II ）由（I ）)4sin()(π+=x x f ，所以)4()4()(ππ-⋅+=x f x f x g =sin()sin()4444x x ππππ++⋅-+sin()sin 2x x π=+ ……………8分cos sin x x =⋅ ……………9分 1sin 22x = ……………10分 因为]2,0[π∈x ，所以],0[2π∈x ，]1,0[2sin ∈x故：]21,0[2sin 21∈x ，当4π=x 时，)(x g 取得最大值21. …………… 13分 16. （本小题满分13分） 解：（I ）设“甲获得优惠券”为事件A …………… 1分因为假定指针停在任一位置都是等可能的，而题中所给的三部分的面积相等，所以指针停在20元，10元，0元区域内的概率都是31. …………… 3分 顾客甲获得优惠券，是指指针停在20元或10元区域，根据互斥事件的概率，有323131)(=+=A P ， …………… 6分 所以，顾客甲获得优惠券面额大于0元的概率是23.（II ）设“乙获得优惠券金额不低于20元”为事件B …………… 7分 因为顾客乙转动了转盘两次，设乙第一次转动转盘获得优惠券金额为x 元， 第二次获得优惠券金额为y 元，则基本事件空间可以表示为：{(20,20),(20,10),(20,0),(10,20),(10,10),(10,0),(0,20),(0,10),(0,0)}Ω=，…………… 9分 即Ω中含有9个基本事件，每个基本事件发生的概率为91. ………… 10分 而乙获得优惠券金额不低于20元，是指20x y +≥，所以事件B 中包含的基本事件有6个， ………… 11分 所以乙获得优惠券额不低于20元的概率为3296)(==B P ………… 13分 答：甲获得优惠券面额大于0元的概率为32，乙获得优惠券金额不低于20元的概率为32. 17. （本小题满分14分）证明：(Ⅰ) 因为ABCD 为菱形，所以AB=BC又60ABC ∠=，所以AB=BC=AC ， ……………1分 又M 为BC 中点，所以BC AM ⊥ …………… 2分 而PA ⊥平面ABCD ，BC ⊂平面ABCD ,所以PA BC ⊥ …………… 4分 又PA AM A = ，所以BC ⊥平面AMN …………… 5分（II ）因为11122AMC S AM CM ∆=⋅== …………… 6分 又PA ⊥底面,ABCD 2,PA = 所以1AN = 所以，三棱锥N AMC -的体积31=V AMCS AN ∆⋅ ………… 8分11326=⨯=………… 9分 (III)存在 …………… 10分取PD 中点E ，连结NE ，EC,AE, 因为N ，E 分别为PA ，PD 中点，所以AD NE 21// …………… 11分 又在菱形ABCD 中，1//2CM AD 所以MC NE //，即MCEN 是平行四边形 …………… 12分 所以， EC NM //，又⊂EC 平面ACE ，⊄NM 平面ACE所以MN //平面ACE ， …………… 13分 即在PD 上存在一点E ，使得//NM 平面ACE ，此时12PE PD ==. …………… 14分 18. （本小题满分14分） 解：（I ）因为(1)0,(1)0f g ==，所以点)0,1(同时在函数)(),(x g x f 的图象上 …………… 1分 因为x a x g x x f ln )(,1)(2=-=， '()2f x x =， ……………3分'()ag x x=……………5分 由已知，得)1(')1('g f =，所以21a=，即2a = ……………6分（II ）因为x a x x g x f x F ln 21)(2)()(2--=-=（)0>x ……………7分所以xa x x a x x F )(222)('2-=-= ……………8分 当0<a 时，因为0>x ，且,02>-a x 所以0)('>x F 对0>x 恒成立，所以)(x F 在),0(+∞上单调递增，)(x F 无极值 ……………10分； 当0>a 时，令0)('=x F ，解得12x x =（舍） ……………11分 所以当0x >时，'(),()F x F x 的变化情况如下表：……………13分 所以当a x =时，()F x 取得极小值，且a a a a a a a F ln 1ln 21)()(2--=--=. ……………14分综上，当0<a 时，函数)(x F 在),0(+∞上无极值；当0>a 时，函数()F x 在a x =处取得极小值a a a ln 1--.19. （本小题满分13分）解：（I ）设椭圆C 的方程为22221,(0)x y a b a b+=>>，由题意可得 21==a c e ,又222c b a +=，所以2243a b =……………2分 因为椭圆C 经过（1，32），代入椭圆方程有 14349122=+a a解得2=a ……………4分所以1c = ，2413b =-=故椭圆C 的方程为 22143x y +=. ……………5分 （Ⅱ）解法一：当直线l x ⊥轴时，计算得到：33(1,),(1,)22A B ---，1113||||13222AOB S AB OF ∆=⋅⋅=⨯⨯=，不符合题意. ……………6分当直线l 与x 轴不垂直时，设直线l 的方程为：(1)y k x =+,0≠k由22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，消去y ，得 2222(34)84120k x k x k +++-= …………7分 显然0∆>成立，设1122(,),(,)A x y B x y ，则21228,34k x x k +=-+ 212241234k x x k-⋅=+ ……………8分又2212221221221)()()()(||x x k x x y y x x AB -+-=-+-==== ……………9分 即2212(1)||34k AB k+==+ 又圆O的半径r ==……………10分所以2221112(1)6|||2234347AOBk k S AB r k k ∆+=⋅⋅=⋅==++……………11分 化简，得4217180k k +-=，即22(1)(1718)0k k -+=， 解得2212181,17k k ==-（舍） ……………12分所以，2r ==，故圆O 的方程为：2212x y +=. ……………13分（Ⅱ）解法二：设直线l 的方程为 1x ty =-，由221143x ty x y =-⎧⎪⎨+=⎪⎩，消去x ，得 22(43)690t y ty +--= ……………7分因为0∆>恒成立，设1122(,),(,)A x y B x y ， 则12122269,4343t y y y y t t +=⋅=-++ ……………8分所以12||y y -==243t =+ ……………9分所以1121||||2AOBS FO y y ∆=⋅⋅-==化简得到4218170t t --=，即0)1)(1718(22=-+t t ，解得211,t=2217 18t=-（舍）…………11分又圆O的半径为r==……………12分所以2r==，故圆O的方程为：2212x y+=……………13分.20.（本小题满分13分）解：（Ⅰ）因为11a=，所以21123a a=+=，3115222a a=+=，42127a a=+=,52113222a a=+=…………3分（Ⅱ）由题意，对于任意的正整数n，121nnb a-=+，所以121nnb a+=+…………4分又122221(21)12(1)2n n n na a a b-+=++=+=所以12n nb b+=…………6分又11112112b a a-=+=+=…………7分所以{}n b是首项为2，公比为2的等比数列，所以2nnb=…………8分（III）存在. 事实上，对任意的*2,m k N≥∈，在数列{}na中，2,21,22,221....,m m m m ma a a a+++-这连续的2m项就构成一个等差数列……10分我们先来证明：“对任意的*2,n n N≥∈，1*(0,2),nk k N-∈∈，有12212nnkka-+=--”由（II）得1212nnnb a-=+=，所以1221nna-=-.当k为奇数时，1121221222112222n n n kk ka a a----++-+=+=+当k为偶数时，112222221212n n n kk ka a a---+++=+=+记1,,21,,2kkkkk⎧⎪⎪=⎨-⎪⎪⎩为偶数为奇数因此要证12212n nk k a -+=--，只需证明21112212n n k k a --+=--，其中2*11(0,2),n k k N -∈∈ (这是因为若21112212n n k k a --+=--，则当211-=k k 时，则k 一定是奇数，有1121221222112222n n n k k k a a a ----++-+=+=+=212)22112(221)212(221111k k k n n n --=---+=--+--； 当21kk =时，则k 一定是偶数，有112222221212n n n k k k a a a ---+++=+=+=212)2212(21)212(21111kkk n n n --=--+=--+-- )如此递推，要证21112212n n k k a --+=--， 只要证明32222212n n k k a --+=--，其中11211,,21,,2k k k k k ⎧⎪⎪=⎨-⎪⎪⎩为偶数为奇数，3*22(0,2),n k k N -∈∈如此递推下去， 我们只需证明12222212n n k k a --+=--， 1*22(0,2),n n k k N --∈∈ 即1221115213222a +=--=-=，即352a =，由（I ）可得， 所以对*2,n n N ≥∈，1*(0,2),n k k N -∈∈，有12212n n k ka -+=--，对任意的*2,m m N ≥∈ ，12212m m i i a ++=--，1211212m m i i a ++++=--，其中*),12,0(N i i m ∈-∈， 所以21212m m i i a a +++-=-又1212-=+m m a ，2112112--=++m m a ，所以21212m m a a +-=- 所以2,21,22,221....,m m m m m a a a a +++-这连续的2m项， 是首项为1221m m a +=-，公差为12-的等差数列 . …………13分说明：当12m m >（其中**1122,,m m N m N ≥∈∈）时，因为1222212222222,...,,,-+++m m m m m a a a a构成一个项数为22m 的等差数列，所以从这个数列中任取连续的12m 项，也是一个项数为12m ，公差为12-的等差数列.。

北京市海淀区2010年一模第1页北京市海淀区2010年抽样测试初三数学试卷 2010.5一、选择题(本题共32分, 每小题4分)下面各题均有四个选项, 其中只有一个是符合题意的．1．的倒数是21-A. 2B.C.D.2-2121-2．2010年2月12日至28日，温哥华冬奥会官方网站的浏览量为275 000 000人次. 将275 000 000用科学记数法表示为A.B.C.D.72.7510⨯727.510⨯82.7510⨯90.27510⨯3.右图是某几何体的三视图，则这个几何体是A. 圆柱 B. 正方体C. 球D. 圆锥4.一个多边形的内角和是外角和的2倍，则这个多边形的边数为A. 5 B.6 C. 7D.85．一个布袋中有4个除颜色外其余都相同的小球，其中3个白球，1个红球．从袋中任意摸出1个球是白球的概率是A ．43B ．41C ．32D ．316．四名运动员参加了射击预选赛，他们成绩的平均环数及其方差如表所示．如果x 2s 选出一个成绩较好且状态稳定的人去参赛，那么应选A ．甲B ．乙C ．丙D ．丁7．把代数式 分解因式，结果正确的是322363x x y xy -+A ．B ．(3)(3)x x y x y +-223(2)x x xy y -+C ．D ．2(3)x x y +23()x x y -8. 如图,点、是以线段为公共弦的两条圆弧的中点，. 点、分别为E F BC 6BC =A D 线段、上的动点. 连接、，设，，EF BC AB AD BD x =22AB AD y -=下列图象中，能表示与的函数关系的图象是yxA ．B ．C ．D ．北京市海淀区2010年一模第3页二、填空题(本题共16分, 每小题4分)9.函数的自变量的取值范围是．13-=x y x 10.如图, 的半径为2，点为上一点，弦于点，,O A A O A OD ⊥BC D 1OD =则________BAC ∠=︒11.若代数式可化为，则的值是．26x x b -+2()1x a --b a -12.如图，+1个边长为2的等边三角形有一条边在同一直线上，n 设△的面积为，△的面积为，…，△的面积为，211B D C 1S 322B D C 2S 1n n n B D C +n S 则=；=____(用含的式子表示)．2S n S n 三、解答题(本题共30分, 每小题5分)13.．112cos301)()2-︒+--14.解方程：．23233x x x +=-+15.如图, △和△均为等腰直角三角形，, 连接、OAB COD 90AOB COD ∠=∠=︒AC .求证: .BD AC BD =16.已知：，求代数式的值. 17. 已知：如图，一2310x x +=2(2)(10)5x x x -++-次函数与反比例函数的图象在第一象限的交点为．y x m =+y =(1)A n ，(1)求与的值；m n (2)设一次函数的图像与轴交于点，连接，求的度数．x B OA BAO ∠北京市海淀区2010年一模第5页18.列方程(组)解应用题：2009年12月联合国气候会议在哥本哈根召开．从某地到哥本哈根，若乘飞机需要3小时，若乘汽车需要9小时．这两种交通工具平均每小时二氧化碳的排放量之和为70千克，飞机全程二氧化碳的排放总量比汽车的多54千克，分别求飞机和汽车平均每小时二氧化碳的排放量．四、解答题(本题共20分, 第19题6分, 第20、21题每小题5分, 第22题4分)19.已知：如图，在直角梯形中，∥，，于点ABCD AD BC ︒=∠90DCB BD AC ⊥O ，，求的长.4,2==BC DC AD20.已知：如图，为的外接圆，O A ABC ∆为的直径，作射线，使得平分BC O A BF BA ，过点作于点.CBF ∠A AD BF ⊥D (1)求证：为的切线；DA O A (2)若，，求的半径.1BD =1tan 2BAD ∠=O AC21. 2009年秋季以来，我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分.图1图2请根据以上信息解答问题：(1)补全图1和图2；(2)如果全校学生家庭总人数约为3000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量.22.阅读：如图1，在和中，,ABC ∆DEF ∆90ABC DEF ∠=∠=︒ , 、、、 四点都在直线上，,AB DE a ==BC EF b ==()b a <B C D E m 点与点重合. 连接、，B D AE FC 我们可以借助于和的大小关系证明不等式：().ACE S ∆FCE S ∆222a b ab +>0b a >>证明过程如下:∵,,.BC b BE a EC b a ===-∴ 11(),22ACE S EC AB b a a ∆=⋅=-11().22FCE S EC FE b a b ∆=⋅=-∵,0b a >>∴.FCE S ACE S ∆∆>即.a a b b a b )(21)(21->-∴. ∴.22b ab ab a ->-222a b ab +>解决下列问题：(1)现将△沿直线向右平移，设DEF m 当时, .BD EC =k =利用此图,仿照上述方法,证明不等式：().222a b ab +>0b a >>(2)用四个与全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式.请ABC ∆北京市海淀区2010年一模第7页你画出一个示意图，并简要说明理由.五、解答题(本题共22分, 第23题7分, 第24题8分, 第25题7分)23.关于的一元二次方程有实数根，且为正整数.x 240x x c -+=c (1)求的值；c (2)若此方程的两根均为整数，在平面直角坐标系中,抛物线与xOy 24y x x c =-+轴交于、两点(在左侧)，与轴交于点. 点为对称轴上一点，且x A B A B y C P 四边形为直角梯形，求的长；OBPC PC (3)将(2)中得到的抛物线沿水平方向平移，设顶点的坐标为,当抛物线与(2)D (),m n 中的直角梯形只有两个交点，且一个交点在边上时，直接写出的取OBPC PC m 值范围.24.点为抛物线(为常数，)上任一点，将抛物线绕顶点P 222y x mx m =-+m 0m >逆时针旋转后得到的新图象与轴交于、两点(点在点的上方)，G 90︒y A B A B 点为点旋转后的对应点.Q P (1)当，点横坐标为4时，求点的坐标；2m =P Q (2)设点，用含、的代数式表示；(,)Q a b m b a (3) 如图，点在第一象限内, 点在轴的正半轴上，点为的中点， 平Q D x C OD QO 分，，当时，求的值.AQC ∠2AQ QC =QD m =m北京市海淀区2010年一模第9页25.已知：中，，中，,AOB △2AB OB ==COD △3CD OC ==. 连接、，点、、分别为、、的ABO DCO =∠∠AD BC M N P OA OD BC 中点.图(1) 如图1，若、、三点在同一直线上，且，A O C 60ABO =∠则的形状是________________，此时________；PMN △ADBC=(2) 如图2，若、、三点在同一直线上，且，A O C 2ABO α=∠证明，并计算的值(用含的式子表示)；PMNBAO △∽△ADBCα(3) 在图2中，固定，将绕点旋转，直接写出的最大值.AOB △COD △O PM海淀区九年级第二学期期中测评数学试卷答案及评分参考一、选择题（本题共32分，每小题4分）题号12345678答案B C D B A B D C 二、填空题（本题共16分，每小题4分）题号9101112答案605三、解答题（本题共30分，每小题5分）13．计算：.解：原式=----------------------------------4分=.---------------------------------5分14．解方程：.解：去分母，得． ---------------------------------1分去括号，得． ---------------------------------2分解得． ---------------------------------4分经检验，是原方程的解．∴原方程的解是． ---------------------------------5分15．证明：∵∴---------------------------------1分∵△与△均为等腰三角形，∴---------------------------------3分北京市海淀区2010年一模第11页在△和△中，∴△≌△.---------------------------------4分∴.---------------------------------5分16．解：原式=---------------------------------2分=.---------------------------------3分当时，原式=---------------------------------4分.---------------------------------5分17．解：（1）∵点在双曲线上，∴.---------------------------------1分又∵在直线上，∴.---------------------------------2分（2）过点A作AM⊥x轴于点M.∵直线与轴交于点，∴.解得.∴点的坐标为.∴.---------------------------------3分∵点的坐标为，∴.在Rt△中，,∴.∴.---------------------------------4分由勾股定理，得.∴∴.∴.---------------------------------5分18．解：设乘飞机和坐汽车每小时的二氧化碳排放量分别是x千克和y千克. ………1分依题意，得---------------------------------2分解得----------------------------4分答: 飞机和汽车每小时的二氧化碳排放量分别是57千克和13千克. ………5分四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）19．解法一：过点作交的延长线于点.---------------------------------1分∴.∵于点,北京市海淀区2010年一模第13页∴.∴. ---------------2分∵，∴四边形为平行四边形. ---------------3分∴.∵，∴.-------------------------------4分∵，∴.∴.---------------------------------5分解法二：，.又，. --------------------------------------------1分于点,....------------------------------------------2分.---------------------------------------------3分在Rt△中，.在Rt△中，..------------------------------------------4分,，. ---------------------------------------------5分20. （1）证明：连接. ---------------------------------1分∵，∴.∵，∴.∴ .∴∥.--------------------------2分∵,∴.∴.∵是⊙O半径，∴为⊙O的切线. ---------------------------------3分（2）∵,，，∴.由勾股定理，得. --------------------------------4分北京市海淀区2010年一模第15页∴.∵是⊙O直径，∴.∴.又∵, ,∴.在Rt △中，==5.∴的半径为.-------------------------5分(1)21. 解：--------------------------4分(2) 全体学生家庭月人均用水量为--------------------------5分（吨）.答：全校学生家庭月用水量约为9040吨.--------------------------6分22．（1）；--------------------------1分证明：连接、.可得.∴，.∵，∴，即.∴.∴.--------------------------2分（2）答案不唯一，图1分，理由1分.举例：如图，理由：延长BA、FE交于点I.∵，∴，北京市海淀区2010年一模第17页即.∴.∴.--------------------------4分举例：如图，理由：四个直角三角形的面积和，大正方形的面积.∵，∴.∴.--------------------------4分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23．解：（1）∵关于的一元二次方程有实数根，∴△=.∴-----------------------1分又∵为正整数，∴. ------------------- 2分（2）∵方程两根均为整数，∴.---------------3分又∵抛物线与x轴交于A、B两点，∴.∴抛物线的解析式为.--------------4分∴抛物线的对称轴为.∵四边形为直角梯形，且，∴∥.∵点在对称轴上，∴.--------------5分（3）或.----------- 7分（写对一个给1分）24. 解：（1）当m=2时，，则，. --------------------1分如图，连接、,过点作轴于,过点作轴于.依题意,可得△≌△.则∴.∴. ------------------2分（2）用含的代数式表示：. ------4分（3）如图，延长到点E，使,连接.∵为中点,∴.∵,∴△≌△.∴. ------------------5分∵,∴.∵平分,北京市海淀区2010年一模第19页∴.∴△≌△. ------------------6分∴.∴.------------------7分∵在新的图象上,∴.∴，（舍）.∴. ------------------8分25. 解：(1)等边三角形，1；(每空1分) ------------------------2分（2）证明：连接、.由题意，得，,.∵、、三点在同一直线上，∴、、三点在同一直线上.∴.∵为中点，∴在Rt △中，.在Rt △中，.∴.---------------------------3分∴、、、四点都在以为圆心，为半径的圆上.∴.又∵，∴.∴. ----------------------------------4分∴.由题意，，又.∴.------------------------------------5分∴.在Rt中，.∵，∴.∴.------------------------------6分（3）.--------------------------------7分(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。

海淀区高三年级第一学期期末练习数 学 (文科) 2011.1第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1．的值为A ．B ．C ．D ． 2. 若等差数列的前项和为n S ，且，则4S 的值为A. 12B.11C.10D. 9 3. 设为两个不同的平面，直线，则“”是“”成立的 A ．充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4. 某部门计划对某路段进行限速，为调查限速60 km/h 是否合理，对通过该路段的300辆汽车的车速进行检测，将所得数据按40，50)，，，分组，绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有A.75辆B.120辆C.180辆D.270辆 5.点在不等式组表示的平面区域内， 则点到直线距离的最大值为A.2B.C.D.8 6. 一空间几何体的三视图如图所示,则该几何体的体 积为A ．12B ．6C ． 4D ．2 7. 已知函数，（），那么下面结论正确的是A ．在上是减函数 B. 在上是减函数 C. , D. ,8. 已知椭圆：，对于任意实数k ，下列直线被椭圆所截弦长与l ：被椭圆所截得的弦长不可．．能．相等的是 A ． B ． C ． D ．二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9. 若直线l 经过点（1，2）且与直线平行,则直线l 的方程为__________.正视图左视图俯视图10.某程序的框图如图所示，执行该程序，若输入4，则输出的S为.11．椭圆的右焦点的坐标为.则顶点在原点的抛物线C的焦点也为，则其标准方程为.12．在一个边长为1000米的正方形区域的每个顶点处设有一个监测站，若向此区域内随机投放一个爆破点，则爆破点距离监测站200米内都可以被检测到.那么随机投入一个爆破点被监测到的概率为_______.13已知向量.若与垂直, 则.14．在平面直角坐标系中，为坐标原点.定义、两点之间的“直角距离”为为. 若点，则= ；已知，点M为直线上动点，则的最小值为.三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15．（本小题满分13分）设函数，.（I）求函数的周期和值域；（II）记的内角的对边分别为，若且，求角C的值.16. （本小题满分13分）某学校三个社团的人员分布如下表（每名同学只参加一个社团）学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果围棋社被抽出12人.(I) 求这三个社团共有多少人？(II)书法社从3名高中和2名初中成员中，随机选出2人参加书法展示，求这2人中初、高中学生都有的概率.17. （本小题满分13分）如图，棱柱ABCD—的底面为菱形，，侧棱⊥BD,点F为的中点．（I）证明：平面；（II）证明：平面平面.18. （本小题满分13分）已知函数其中.（I）若曲线在处的切线与直线平行，求的值；（II）求函数在区间上的最小值.19. （本小题满分14分）已知圆,点为直线上的动点.(I)若从到圆的切线长为，求点的坐标以及两条切线所夹劣弧长；（II）若点，直线与圆的另一个交点分别为,求证:直线经过定点.20. （本小题满分14分）已知集合.对于A的一个子集S，若存在不大于的正整数m，使得对于S中的任意一对元素，都有，则称S具有性质P.（Ⅰ）当时，试判断集合和是否具有性质P？并说明理由.(II)若集合S具有性质P，试判断集合)是否一定具有性质P？并说明理由.海淀区高三年级第一学期期末练习数学（文）答案及评分参考2011．1第Ⅰ卷（选择题共40分）一、选择题（本大题共8小题,每小题5分,共40分）第II卷（非选择题共110分）二、填空题（本大题共6小题,每小题5分, 共30分.有两空的题目，第一空3分，第二空2分）9. 10. 19 11.12. 13. 2 14. 4 3三、解答题(本大题共6小题,共80分)15．（共13分）解：（I），............................... 3分的周期为（或答:）. ................................4分因为，所以,所以值域为. ...............................5分（II）由（I）可知，, ...............................6分, ...............................7分,, ..................................8分得到. ...............................9分且, ....................................10分, , ....................................11分，. ....................................12分. ....................................13分16. （共13分）解：（I）围棋社共有60人，...................................1分由可知三个社团一共有150人. ...................................3分（II）设初中的两名同学为，高中的3名同学为, ...................................5分随机选出2人参加书法展示所有可能的结果:，共10个基本事件. ..................................8分设事件表示“书法展示的同学中初、高中学生都有”，..................................9分则事件共有6个基本事件....................................11分.故参加书法展示的2人中初、高中学生都有的概率为. ................................13分17. （共13分）解：（I）四边形ABCD为菱形且，是的中点. ...................................2分又点F为的中点,在中，, ...................................4分平面，平面,平面. ...................................6分（II）四边形ABCD为菱形,, ...................................8分又，且平面,.................................10分平面, ................................11分平面,平面平面. ................................13分18. （共13分）解：，. .........................................2分（I）由题意可得，解得，........................................3分此时，在点处的切线为，与直线平行.故所求值为1. ........................................4分（II）由可得，，........................................ 5分①当时，在上恒成立，所以在上递增，.....................................6分所以在上的最小值为. ........................................7分②当时，....................................10分由上表可得在上的最小值为. ......................................11分③当时，在上恒成立，所以在上递减. ......................................12分所以在上的最小值为. .....................................13分综上讨论，可知：当时，在上的最小值为；当时，在上的最小值为；当时，在上的最小值为.19. （共14分）解：根据题意，设.(I)设两切点为，则，由题意可知即，............................................2分解得，所以点坐标为. ...........................................3分在中，易得，所以. ............................................4分所以两切线所夹劣弧长为. ...........................................5分（II）设，，依题意，直线经过点，可以设，............................................6分和圆联立，得到，代入消元得到，， ......................................7分因为直线经过点，所以是方程的两个根，所以有，，..................................... 8分代入直线方程得，. ..................................9分同理，设，联立方程有，代入消元得到，因为直线经过点，所以是方程的两个根，，，代入得到. .....................11分若，则，此时显然三点在直线上，即直线经过定点............................12分若，则，，所以有，................13分所以，所以三点共线，即直线经过定点.综上所述，直线经过定点. .......................................14分20. （共14分）解：（Ⅰ）当时，集合，不具有性质. ...................................1分因为对任意不大于10的正整数m，都可以找到集合中两个元素与，使得成立. ...................................3分集合具有性质. ....................................4分因为可取，对于该集合中任意一对元素，都有. ............................................6分（Ⅱ）若集合S具有性质，那么集合一定具有性质. ..........7分首先因为，任取其中，因为，所以，从而，即所以...........................8分由S具有性质，可知存在不大于的正整数m，使得对S中的任意一对元素，都有，..................................9分对上述取定的不大于的正整数m，从集合中任取元素，其中，都有；因为，所以有，即所以集合具有性质．.............................14分文档供参考，可复制、编制，期待您的好评与关注！说明：其它正确解法按相应步骤给分.11 / 11。

2010年北京海淀区高考一模试题：数学（文）(4)一、选择题（共6小题；共30分）1. 一个体积为的正三棱柱的三视图如图所示，则这个三棱柱的左视图的面积为______A. B. C. D.2. 在复平面内，复数（是虚数单位）对应的点位于______A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 对于非零向量，，“ ”是“ ”的______A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4. 直线与圆相交于，两点（其中是实数），且是直角三角形（是坐标原点），则点与点之间距离的最大值为______A. B. C. D.5. 已知等差数列的前项和为，且满足，则数列的公差是______A. B. C. D.6. 在同一坐标系中画出函数，，的图象，可能正确的是______A. B.C. D.二、填空题（共3小题；共15分）7. 某校为了解高三同学寒假期间学习情况，抽查了名同学，统计他们每天平均学习时间，绘成频率分布直方图（如图）．则这名同学中学习时间在到小时内的人数为______．8. 已知动点到定点的距离和它到定直线：的距离相等，则点的轨迹方程为______．9. 已知不等式组表示的平面区域的面积为，点在所给平面区域内，则的最大值为______．三、解答题（共3小题；共39分）10. 如图，在四棱锥中，底面是菱形，，平面，点，分别为、的中点，且．（1）证明：平面；（2）求三棱锥的体积；（3）在线段上是否存在一点，使得 平面 ? 若存在，求出的长；若不存在，说明理由．11. 已知函数，（其中，，），其部分图象如图所示．（1）求的解析式；（2）求函数在区间上的最大值及相应的值．12. 已知函数与函数．（1）若的图象在点处有公共的切线，求实数的值；（2）设，求函数的极值．四、选择题（共2小题；共10分）13. 的值为______A. B. C. D.14. 给出下列四个命题：①若集合、满足，则；②给定命题，，若" "为真，则" "为真；③设，若，则；④若直线与直线垂直，则．其中正确命题的个数是______A. B. C. D.五、填空题（共2小题；共10分）15. 若，则的最小值是______．16. 已知程序框图如图所示，则执行该程序后输出的结果是______．六、解答题（共1小题；共13分）17. 某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费每满元可以转动如图所示的圆盘一次，其中为圆心，且标有元、元、元的三部分区域面积相等．假定指针停在任一位置都是等可能的．当指针停在某区域时，返相应金额的优惠券．（例如：某顾客消费了元，第一次转动获得了元，第二次获得了元，则其共获得了元优惠券）．顾客甲和乙都到商场进行了消费，并按照规则参与了活动．（1）若顾客甲消费了元，求他获得优惠券面额大于元的概率?（2）若顾客乙消费了元，求他总共获得优惠券金额不低于元的概率?答案第一部分1. A2. A3. A4. A5. C6. D第二部分7.8.9.第三部分10. （1）因为为菱形，，所以为正三角形，又为中点，所以．因为平面，平面，所以．又，所以平面．（2）由为的中点，得由为的中点，且，得．又底面，所以三棱锥的体积为（3）在线段上存在点，使得 平面．取中点，连接，，．因为，分别为、中点，所以，．在菱形中，因为为的中点，所以，，于是，，则是平行四边形，所以，又平面，平面，所以平面．因此，当为的中点，且时， 平面．11. （1）由图可知，，，所以，．又且所以，所以（2）由（1），所以因为，所以，．故，当时，取得最大值．12. （1）由已知，得所以点同时在函数与的图象上．再由已知，得根据题意，得解得．（2）由已知，得则有当时，因为，则，所以对恒成立．于是，在上单调递增，无极值；当时，令，结合，解得．所以当时，当时，的变化情况如下表：极小值有极小值，且但没有极大值．综上，当时，在上无极值；当时，在处取得极小值，没有极大值．第四部分13. C 14. B第五部分15.16.第六部分17. （1）设"甲获得优惠券"为事件．因为假定指针停在任一位置都是等可能的，而题中所给的三部分的面积相等，所以指针停在元，元，元区域内的概率都是．顾客甲获得优惠券，是指指针停在元或元区域，根据互斥事件的概率，有．所以，顾客甲获得优惠券面额大于元的概率是．（2）设"乙获得优惠券金额不低于元"为事件．因为顾客乙转动了转盘两次，设乙第一次转动转盘获得优惠券金额为元，第二次获得优惠券金额为元，则基本事件空间可以表示为：即中含有个基本事件，每个基本事件发生的概率为．而乙获得优惠券金额不低于元，是指，所以事件中包含的基本事件有个，所以乙获得优惠券额不低于元的概率为．。