关于检校张拉千斤顶的回归方程式

张拉计算书一、钢绞线的张拉预应力混凝土达到一定强度后拆除模板，砼强度达到100％后，穿钢绞线，用两端张拉法进行张拉，用标定好的千斤顶进行张拉，张拉两端同时进行，确保张拉时两端操作要一致。

①、张拉前的准备工作1）、梁体验收，混凝土强度达到100%后张拉。

穿束张拉前，对构件的质量，几何尺寸等进行检查，预留孔道用通孔器或压气、压水等方法进行检查。

构件端部预埋铁板与锚具和垫板接触处的焊渣，毛刺、混凝土残渣等清理干净。

2）、标定千斤顶油表读数，施工过程中定期检校，依据标定的曲线计算各张拉力对应的油表读数。

3）、穿入钢绞线：对加工好的钢绞线进行编号，钢绞线穿束时，将一端打齐套上穿束器，将穿束器的引线穿过孔道，然后向前拉动，直至两端均露出60cm 的工作长度，穿束后检查两端编号，防止钢绞线在孔道内交叉扭结。

②、预应力的张拉程序预应力钢绞线张拉顺序严格按照图纸要求进行张拉，千斤顶张拉作用线与预应力钢绞线的轴线重合一致。

钢绞线的张拉程序如下：0→15%σk →30%σk →50%σk →100σk →103σk (持荷2分钟) →锚固。

在张拉过程中15%、30%、50%、100%时必须有技术停留，其中15%停留目的是保证钢绞线均匀受力，同时量测其伸长；30%停留并量测其伸长的目的是推测30%已下的伸长量；50%停留是为了保证两端张拉同步进行；100%停留并量测其伸长量;103%时持荷2分钟能有效消除张拉过程中的各种应力损失；钢绞线的实际伸长量与理论伸长值的差值应控制在±6%以内，否则应暂停张拉，分析原因提出解决方案，待监理工程师审批后方可继续张拉。

实际伸长值按以下公式计算：△L=△L1+△L2(mm)△L1=100%的伸长值-15%的伸长值（mm）△L2=30%的伸长值-15%的伸长值（mm）③、张拉的操作步骤四人配备一套张拉顶，一人负责油泵，两人负责千斤顶，一人观测并记录读数，张拉按设计要求的顺序进行，并保证对称张拉。

应用线性回归模型校准液压千斤顶【摘要】本文先介绍了最小二乘法的定义和最小二乘法在线性回归模型中的表示方法。

然后再介绍了最小二乘法的相关公式。

最后利用已经校准的液压千斤顶来检测井盖的破坏荷载是否满足规范要求。

一、最小二乘法与线性回归模型1、最小二乘法的定义在实际工作中，常常会遇到这样的问题：给出两个变量x，y的n组试验数据，怎么才能从中找出变量x、y的函数关系式呢？然后利用这个函数关系式对x与y之间的除了试验数据之外的其它对应情况作出某种判断。

这样的问题一般可以分为两类：一类是对x与y之间所存在的对应规律一无所知，这时要从试验数据中找出符合实际情况的函数关系式是很困难的，这类问题为黑箱问题；另一类是通过问题作出分析，然后再建立数学模型或者通过整理归纳试验数据，得出x与y之间符合某种类型的函数关系式，其中有m个待定参数，这些参数的值可以通过n组试验数据来确定，这类问题称为灰箱问题。

解决灰箱问题的方法通常会利用到“最小二乘法”。

2、最小二乘法在线性回归模型中的表示方法上面我们已经说明了最小二乘法的数据全部来自于试验取得。

在建立一元线性回归方程中，虽然有很多种不同的方法来求样本回归函数，但是在回归分析中最常用的方法就是最小二乘法。

如果变量x与y有精确的线性关系比如说y=kx+b，那么观测值与回归值是相等的。

然而在实际工作中诸多变量的关系不一定都是如此，由于受到许多随机因素的干扰使得物与物之间没有那么明确的一一对应关系。

那么我们就需要通过数学的方法来来使之对应。

首先通过试验取得数据，其次把数据描绘出来。

然后拟合一条跟已知的函数图像最为接近的曲线，这样就可以相对地将他们之间的关系表示出来了。

在处理诸如此类的事件中常常应用到最小二乘法。

3、最小二乘法的适用范围（1）本文所讨论的最小二乘法仅且只适用于一元线性函数，比如y=bx+a。

（2）不适用于非线性函数和多元线性函数。

二、最小二乘法的公式为了定量地给出y=bx+a与实验数据之间线性关系的符合程度，可以用Pearson（皮尔逊）相关系数R来衡量。

20% 30% 50% 100% 15%
17束
3296.4
30% 50% 100%
计量器具名称及型号：液压千斤顶，400t 出厂编号：0937 压力表器号：5203.14D 油泵型号：ZB10/320-4/800B 油泵器号： 校核方程：Y= 钢束股数 0723 0.0134 锚下控制张 拉力（kn） X + -0.38 对应油表 读数 2.94 6.26 10.69 21.76 3.52 5.47 7.42 11.31 19.11 38.60 6.25 12.87 21.71 43.79 0936 5203.14D 型号：ZB10/320-4/800B 器号：0723 千斤顶 出厂编号 对应压力表器号 油泵型号及器号
计量器具名称及型号：液压千斤顶，400t 出厂编号：0938 压力表器号：5382.14D 油泵型号：ZB10/320-4/800B 油泵器号： 校核方程：Y= 钢束股数 0723 0.0133 锚下控制张 拉力（kn） X + -0.1 对应油表 读数 3.20 6.49 10.89 21.88 3.77 5.70 7.64 11.51 19.24 38.58 6.48 13.05 21.82 43.74 0935 5382.14D 型号：ZB10/320-4/800B 器号：0723 千斤顶 出厂编号 对应压力表器号 油泵型号及器号
张拉阶段及对应控制力 （kn） 15% 247.89 495.78 826.3 1652.6 290.86 436.29 581.72 872.58 1454.3 2908.6 494.46 988.92 1648.2 3296.4
9束
1652.6
30% 50% 100% 10% 15%
15束

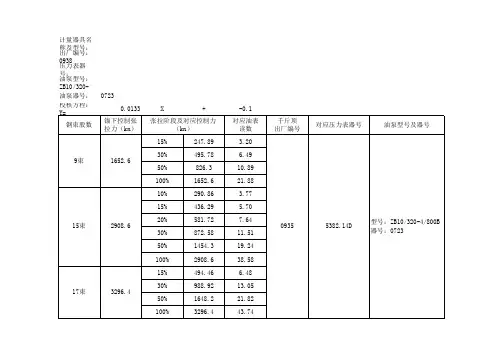
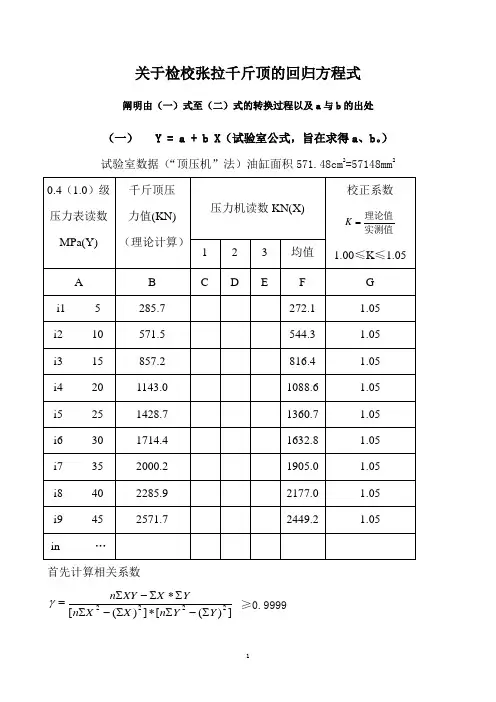
关于检校张拉千斤顶的回归方程式阐明由（一）式至（二）式的转换过程以及a 与b 的出处（一） Y = a + b X （试验室公式，旨在求得a 、b 。

） 试验室数据（“顶压机”法）油缸面积571.48cm 2=57148mm 2首先计算相关系数])([])([2222Y Y n X X n YX XY n ∑-∑*∑-∑∑*∑-∑=γ ≥0.9999计算公式：截距 222)(X n X X Y X XY a ∑-∑∑*∑-∑*∑=斜率 22)(Xn X XYn Y X b ∑-∑∑-∑*∑= 说明：①“Σ”读“西格玛”是“∑=ni 11”的简化。

表示与a 、b 相关的数据（即“回归因素”）Y 或X 由 i 1=5MPa(或272.1KN)……至i 9=45MPa(或2449.2KN)……i n =……之总和。

② n 表示数据量即因数发生的次数，此处n=9。

例如：22229124515105+++=∑= i y 。

()22914515105+++=⎪⎭⎫ ⎝⎛∑= i y 。

()2.2449454.816153.544101.2725991⨯+⨯+⨯+⨯=∑= i YX n 。

③ i 表示因素发生的次序，如i 1=5 ， i 2=10 ……i 9=45等等（因素：原因要素）。

④按公式计算求得Y = a + b X = 0 + 0.018373 X = 0.018373X回归方程（即经验方程、经验公式）之意义（使用价值）在于将各个处于离散分布状态的相关数据（因素）通过统计手段（如a 、b 计算公式）使它们趋于（回归于）统一稳定（如ρ = a + b F 方程式）。

因此，这种回归分析所得数据永远是一个近似数。

其近似于理想值（或理想状态、要求精度）的程度由相关系数γ表达，此处要求γ=0.9999，同时要求校正系数K等于1小于1.05，就是说当γ和K的条件满足后，a、b的运算结果可信（可以在实际生产、工作中应用）。

15-17
设计张拉力(MN) 3.261 19.304 39.358 总监办：
SF匝道桥第二联13束钢绞线液压千斤顶线性回归方程 千斤顶编号 线性回归方程 400T 钢束规格 初应力（10%）Mpa 初应力（50%）Mpa 设计应力（100%）Mpa 15-17 401 油表编号 P=12.6256F+0.43 设计张拉力(MN) 3.636 16.458 32.485
201110531
15-17
设计张拉力(MN) 3.261 19.304 39.358 总监办：
3.1248
驻地监理：
SF匝道桥第二联16束钢绞线液压千斤顶线性回归方程 千斤顶编号 线性回归方程 400T 钢束规格 初应力（10%）Mpa 初应力（50%）Mpa 设计应力（100%）Mpa 15-17 401 油表编号 P=12.6256F+0.43 设计张拉力(MN) 4.375 20.156 39.882施工单位：Fra bibliotek驻地监理：
总监办：
顶线性回归方程 201110631
P=12.6256F+0.43 3.1248 4.375 20.156 39.882
201110626
P=12.7439F+0.34 3.1248 4.322 20.251 40.162
201110544
P=12.7342F-0.48 3.1248 3.499 19.416 39.312
千斤顶编号 线性回归方程 400T 钢束规格 初应力（10%）Mpa 初应力（50%）Mpa 设计应力（100%）Mpa
401
油表编号 P=12.7439F+0.34
201110626
15-17

a）构造与工作原理； b）加撑脚后的外貌 1一张拉油缸；2—顶压油缸（即张拉活塞）；3—顶压活塞；4—弹簧； 5—预应力筋；6—工具锚；7—螺帽；8—锚环；9—构件；10—撑脚； 11一张拉杆；12—连接器；13—张拉工作油室；14—顶压工作油室； 15—张拉回程油室；16—张拉缸油嘴；17一顶压缸油嘴；18—油孔
1-张拉油缸；2-顶压油缸（张拉活塞）；3-顶压活塞；4-弹簧； 5-预应力筋；6-楔块；7-对中套；8-锚塞；9-锚环；10-构件
（三）拉杆式千斤顶
• 拉杆式千斤顶用于螺母锚具、锥形螺杆锚具、钢丝镦 头锚具等。它由主油缸、主缸活塞、回油缸、回油活 塞、连接器、传力架、活塞拉杆等组成。 • 目前常用的一种千斤顶是YL60型拉杆式千斤顶。另外, 还生产YL400型和YL500型千斤顶，其张拉力分别为4 000 kN和5 000 kN，主要用于张拉力较大的钢筋张拉。 • 下图是用拉杆式千斤顶张拉时的工作示意图。
图4-29 YC-60型千斤顶具和JM型锚的安装 1—工作锚；2—YC-60型千斤顶；3—工具锚；4—预应力筋束
• 其工作原理是：张拉预应力筋时，张拉缸油嘴进 油、顶压缸油嘴回油，顶压油缸、连接套和撑套 连成一体右移顶住锚环；张拉油缸、端盖螺母及 堵头和穿心套连成一体带动工具锚左移张拉预应 力筋；顶压锚固时，在保持张拉力稳定的条件下， 顶压缸油嘴进油，顶压活塞、保护套和顶压头连 成一体右移将夹片强力顶入锚环内；此时张拉缸 油嘴回油、顶压缸油嘴进油、张拉缸液压回程。 最后，张拉缸、顶压缸油嘴同时回油，顶压活塞 在弹簧力作用下回程复位。 • 大跨度结构、长钢丝束等引伸量大者，用穿心式 千斤顶为宜。
张拉千斤顶工作原理 及校验 一、张拉千斤顶的工作 原理
•
桥梁工程中施加预应力所用的机具设备通常称为 张拉设备。常用的张拉设备由油压千斤顶和配套的高压 油泵、压力表及外接油管组成。液压千斤顶按其构造可 分为台式（普通油压千斤顶）、穿心式、锥锚式和拉杆 式。工地上比较常见的张拉千斤顶一般为穿心结构，其 主要结构包括张拉外套、活塞、油室，纵剖面结构示意 如图所示。 • 千斤顶在张拉时，将其抵住工作锚具，将工作锚具安装 在活塞前端，并安装工作、工具夹片，通过张拉油泵向 进油嘴进油，在高压油的推动作用下，使活塞向前运动， 在工具锚作用下，带动钢束向前运动，实现钢束的张拉。 • 油室内油压的大小通过张拉油泵上的油表读出。

• 3．千斤顶校验的方法 • 校验应在经主管部门授权的法定计量技术机构进行。 • （1）校验用的标准仪器的精度不得低于1%，压力表 的精度不宜低于1.5级，最大量程不宜小于设备额定张 拉力的1.3倍，校验时，千斤顶活塞运行方向应与实际 张拉工作状态一致。 • （2）千斤顶的校验可以根据现场实际情况，采用压力 机、已经标定的传感器进行标定； • （3） 标定时应将油压表、千斤顶等配套标定； • （4）在标定千斤顶时，应注意千斤顶的工作状态和实 际相同，即让千斤顶顶压力机，不能让压力机压千斤 顶的活塞；
千斤顶构造原理图
• 1）用长柱压力试验机校验 • 校验时，应采取被动校验法，即在校验时用千斤顶顶试 验机，这样活塞运行方向、摩阻力的方向与实际工作时 相同，校验比较准确。 • 在进行被动校验时，压力机本身也有摩阻力，并且与正 常使用时相反，所以，试验机表盘读书反映的也不是千 斤顶的实际作用力。因此用被动法校验千斤顶时，必须 事先用具有足够吨位的标准测力计对试验机进行被动标 定，以确定试验机的表盘读数值。标定后在校验千斤顶 时，就可以从试验机表盘上直接读出千斤顶的实际作用 力以及油压表的准确读数。用压力试验机校验的步骤如 下：
三、检验结果的回归计算
• 千斤顶的作用力T和油缸的油压P的关系是线性关 系，考虑活塞和油缸之间的摩阻力后，它们的关 系可以表示为：
T AP B
•
•
可以利用千斤顶检验测得的作用力和油压
( ( 、T 2 , P2 ) 、T 3 , P3 )、……(T , P ) ， 对上式 式进行线性回归，利用最小二乘法原理求上式的回 归值： ˆ ˆ ˆ T AP B
•
• •
如张拉油缸的面积为A，有活塞力的平衡：
A f N

顶号 0257 表号 548434（7） 张拉力(KN) 油表读数 319.3 10
60
y = 0.035x - 1.564
50
603.9 906.1 1198.2 1432.6
20 30 40 50
40
30
系列1 线性 (系列1)
Y
20
10
0 0 1000 X 2000
顶号 / 表号 548435（8） 张拉力(KN) 油表读数 302.5 10 617.2 20 906.9 30 1194.1 40 1461.4 50
40
30
系列1 线性 (系列1)
Y
20
10
0 0 1000 X 2000
顶号 0255 表号 6A2834（4） 张拉力(KN) 油表读数 293.6 10 592.7 20 894.1 30 1195.2 40 1488.6 50
60
y = 0.033x + 0.164
50
40
30
20
系列1 线性 (系列1)
Y
10
0 0 1000 X 2000
顶号 0250 表号 548432（6） 张拉力(KN) 油表读数 317.9 10 584.8 20 880.8 30 1196.7 40 1431.2 50
60
50
y = 0.035x - 1.025
40
30
系列1 线性 (系列1)
Y
20
10
0 0 1000 X 2000
线性方程：y=aF+b a 0.0358 0.0356 0.035 0.0334 0.0343 0.0352 0.0354 0.0345 b -1.6714 -1.3433 -1.2601 0.1647 -0.859 -1.0254 -1.5645 -0.9417

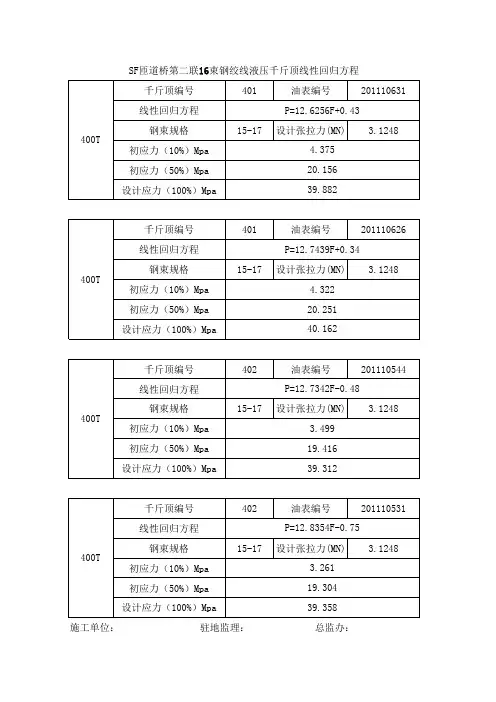
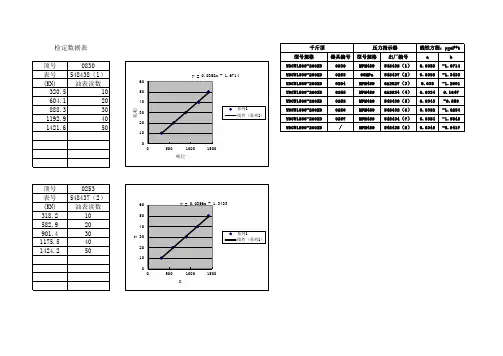
第五章千斤顶校验规程第一节基本原理千斤顶，特别是大吨位千斤顶，常用于预应力砼施工中预应力钢绞线等的张拉。

由于千斤顶对外显示不是活塞上的力值而是液压油的压力值，这样在张拉钢绞线张拉时不方便。

钢绞线的张拉是以力为控制参数的，故校验的第一个任务就是建立千斤顶液压油压力值同千斤顶向外提供的力值之间的关系；一般地，这种关系是线性关系。

另外，由于千斤顶活塞与活塞环之间存在摩擦阻力，单纯以液压油压力来计算千斤顶提供的力值是不恰当的，同时，若活塞与活塞环之间的摩擦阻力过大，也不能保证千斤顶的正确计量，这也是在千斤顶的校验要处理的问题，也就是要限制千斤顶的摩阻系数不大于．．．．。

．．．．．．．．．．．．．1.05一般地，校验千斤顶前，应先校准油压表；只有经校准的油压表才能用在千斤顶上。

在千斤顶上的油压表一般是1.5级精度，这样，在最不利的情况下，互换油压表后的误差也不会超过3.0%，这种精度是能满足施工要求的。

故在理论上用于千斤顶上的油压表可以互换使用，前提条件是油压表必须校准合格。

第二节校验荷载级数确定千斤顶在使用时，往往达不到其最大的吨位，因此在校验时，也不一定要校验到最大吨位。

因此校验荷载级数可这样确定：根据使用要求，确定本次校验的最大压力Pa，则级间压力差为Pa/10，同时，再向最大压力之外加上两荷载级，即两个Pa/10，这样校验荷载级数共有12级。

第三节校验过程1、千斤顶的准备在校验之前，应让千斤顶的活塞自由往复运动数次，一是查看千斤顶是否完好，二是确定千斤顶活塞与活塞环之间是否有异物，造成摩擦阻力过大。

如有故障，应先排除故障。

然后要查找千斤顶的铭牌或档案，查出它的公称活塞面积备用。

2、校验时，将千斤顶置于反力架上，测力计或传感器器置于千斤上方（可选用三等精度的测力计或传感器），用垫块适当地垫高千斤顶或测力计，使用千斤顶活塞能顶上反力架，如图1所示。

启动千斤顶油压泵，使压力表清零。

若是小吨位、小行程的千斤顶，可以用试验室的压力机或万能材料试验机做反力架。

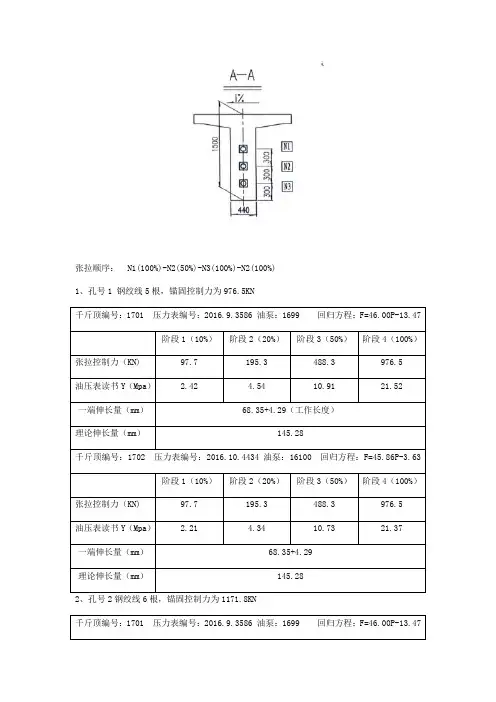
张拉顺序：N1(100%)-N2(50%)-N3(100%)-N2(100%) 1、孔号1 钢绞线5根，锚固控制力为976.5KN2、孔号2钢绞线6根，锚固控制力为1171.8KN3、孔号3钢绞线6根，锚固控制力为1171.8KN锚具变形、钢筋回缩一端按照6mm计算；伸长率=（理论伸长值-（实测伸长值-12mm））/理论伸长值，控制在6%以内。

实测伸长值等于从初应力（10%）到锚固应力（100%）的实测伸长值+初应力以下的推算伸长值（采用相邻级的伸长值，即10%到20%应力的伸长值）。

一、张拉力的计算：根据设计图纸提供φ15.2钢铰线：公称直径d=15.2mm，抗拉强度标准值fpk=1860Mpa，张拉控制应力：σcon=0.75fpk=0.75×1860=1395Mpa；单根钢铰线截面积(查钢绞线质量证明书)为：Ap=140mm2单根钢铰线的张拉力为：P=σcon×Ap=1395×140=195.3KN单束(5根)钢铰线张拉力为：P7=195.3×5=976.5KN单束(6根)钢铰线张拉力为：P8=195.3×6=1171.8KN二、理论伸长值的计算：1、根据《公路桥涵施工技术规范》（JTG/T F50—2011）提供公式：理论伸长值：ΔL=Pp L/ApEp预应力筋平均张拉力计算式：（1）预应力筋为直线时 Pp=P（2）预应力筋为曲线时 Pp=P[1-e-(kx+µθ)]/( kx +µθ) 其中：Pp：平均张拉力（N）L：预应力筋的长度（mm）Ap：预应力筋的截面积（mm2）Ep：预应力筋的弹性模量（N/mm2即Mpa）P：预应力钢绞线张拉端的张拉力（N）x：从张拉端至计算截面孔道长度（m）θ：从张拉端至计算截面曲线孔道部分切线的夹角之和（rad）k：孔道每米局部偏差对摩擦的影响系数μ：预应力钢绞线孔道壁的磨擦系数2、根据设计图纸及材料试验检验提供数据：钢铰线弹性模量Ep=1.95×105Mpa；锚具变形、钢筋回缩按6mm（一端）计算；塑料波纹管摩阻系数μ=0.25 ，偏差系数K= 0.0015；钢绞线一端工作长度为：0.600m，一端伸长量4.29mm。

张拉液压千斤顶原理及校验（20171021(1)）-张力液压千斤顶的原理及验证根据武陵山区区域发展和扶贫规划，湖南湘西作为武陵山区的核心区域，迎来了巨大的发展机遇。

湘西已经启动了一大批国家级和省级重点工程。

作为桥梁施工的重要工具，张拉液压千斤顶的性能直接影响桥梁的质量。

作为在四省边境地区开展千斤顶检定多年的法定检定机构的检定人员，对张拉液压千斤顶的原理及检定进行了简要探讨，以供同行讨论。

一、张紧液压千斤顶的原理。

首先，张紧液压千斤顶是液压系统，包括由电机驱动的高压油泵、高压油管和工作千斤顶。

使用时，高压油泵由电机驱动高速运转，将电能转化为压力能，通过高压油管传递给液压油缸，然后通过液压油缸将压力能转化为机械能，从而达到张紧的目的。

回流喷嘴由高压油管电机驱动高压油泵张力液压千斤顶的简单结构图顶轴油缸的工作千斤顶在日常使用中，当需要顶轴或顶回时，液压油会注入相应的油缸。

它们都符合帕斯卡原理，即F = P SF -油缸工作面上的力值，kN。

压力，MPa。

运行期间，压力值由指示装置显示。

S -油缸的工作表面积，m2。

对于单个液压千斤顶，油缸工作面乘积是常数。

让我们以顶部为例:1.当工作千斤顶未加载时，机油会持续供应至千斤顶油缸。

压力会迫使千斤顶的工作面上升，从而被顶出。

顶轴油缸的容积相应增加，但顶轴油缸内的压力保持不变，顶轴油缸工作面上的力F保持不变。

2.当工作千斤顶加载时，油连续供应到千斤顶油缸。

这种压力会迫使工作千斤顶的工作面上升，从而被堵塞。

顶轴油缸的容积变化不大。

此时，顶轴油缸中的压力P逐渐增大，顶轴油缸工作面上的力F逐渐增大。

但是，油缸中的压力不能无限增加。

根据多年的验证经验，油缸内的压力极限为(50-60)兆帕。

为了获得更大的力值，只能选择油缸工作表面积更大的千斤顶。

因此，在实际工作中，应根据设计要求选择合适的张紧液压千斤顶。

第二，张紧液压千斤顶中液压油的选择。

液压油是液压千斤顶系统中一种重要的传动介质。

论张拉用千斤顶的正校与反校【摘要】预应力张拉千斤顶的校验是预应力结构工程中非常重要的环节，其校正的准确度直接影响建立在结构上的预应力值和结构性能，尤其是小预应力值的张拉更应该重视其千斤顶校验的方法：正校与反校。

【关键词】张拉；预应力值；校验方法；正校与反校0.概述预应力工程用油压千斤顶在张拉过程中，千斤顶因自身密封圈沿缸体的滑移，将会产生一定的摩擦阻力，千斤顶缸内介质的压强数值（油泵压力表示值）乘以其活塞面积（AO）所得的张拉力与实际传递到预应力钢筋的张拉力是不相等的，它们之间存在一个差值（△N）。

尤其是使用大吨位千斤顶张拉小直径钢筋时，其预应力控制的张拉力很小，其差值（△N）对实际张拉控制应力的影响就会更加明显。

在施工中对待如此问题若未能引起重视，则就有可能因预应力钢筋的实际张拉力值与设计要求的控制张拉力之间的偏差数值就会超过规范规定（5%）的要求，导致预应力工程结构质量问题，为了正确有效地解决这一问题，经分析和实践，我们用千斤顶在试验机上进行正校与反校测试，对比结果得出了调整的办法，可有效地消除或减少这种差值而造成影响，其原理和方法仅以某预应力工程用千斤顶的正校与反校来加以说明。

1.千斤顶的正校与反校1.1千斤顶的正校正校就是以千斤顶为主动状态，试验机为被动状态下（也就是以千斤顶顶住试验机的上下压头，开启千斤顶油泵，对处于工作状态下关闭回油阀的试验机上下压头施加力）进行的检（校）验，其结果见表1。

表1千斤顶正校验结果1.2千斤顶的反校反校就是以试验机为主动状态，千斤顶为被动状态下（也就是试验机上下压头给处于工作状态下关闭回油阀的千斤顶施加压力）进行的检（校）验，其结果见表2。

表2千斤顶反校验结果2.正校与反校的比较及注意的问题为了使表2数据与表1数据对应关系更为清楚，将表2数据用插入法简化整理成插入反校数据，在直角坐标系上描点画图其为为两条走向大致相同的直线，并从差值和图中两条直线的走向可以看出，千斤顶压力表压强数值（δB）越大，正校与反校验数据差值（△N）就会逐渐增加，经过分析，增加的原因是由于缸体内压强增大时橡胶密封圈所受压强也会跟着增大，引起变形扭曲等增加，致使阻力也有所增加。