千斤顶回归方程计算式

60吨千斤顶回归方程式
欧伯巴顶是一种常见的悬臂梁设备，它实施了很多重要的工程，这也是一种比
较常见的大型设备。

现在，我们研究的是60吨千斤顶的回归方程式，说明如何计
算其工作效率。

悬臂梁设备的工作原理是通过传动机构，使吊杆上的机头和下方支座间结构，
给吊杆及吊杆上装在钢绞线上的暂停发动机提供动力，利用钢绞线起升吊杆上的吊头。

清楚地知道60吨千斤顶的回归方程式，可以准确计算出其工作效率。

在数学上，60吨千斤顶的回归方程式可以用以下公式表示：M=q*h1*h2/h3，
其中M为吊头重量（60吨），q为起升的速度，h1、h2、h3分别为支座的高度和
绞线的高度。

可以看出，它的计算特别复杂，它是通过不同参数的加权相乘得出的，我们通过改变参数的值来调节工作效率。

此外，60吨千斤顶的回归方程式也允许我们改变设备的结构来实现其燃料消
耗的最小化，从而节约成本。

因此可以看出，60吨千斤顶的回归方程式不仅可以
用来计算其工作效率，还可以用来优化设备的结构，从根本上改善其工作性能。

使用60吨千斤顶的回归方程式可以准确地测试设备的性能，更重要的是，能
够最大程度地提高工作效率，使设备能够实现最低燃料消耗和最优工作绩效。

因此，60吨千斤顶的回归方程式的存在，对于悬臂梁设备的研究和开发，起着重要的作用。

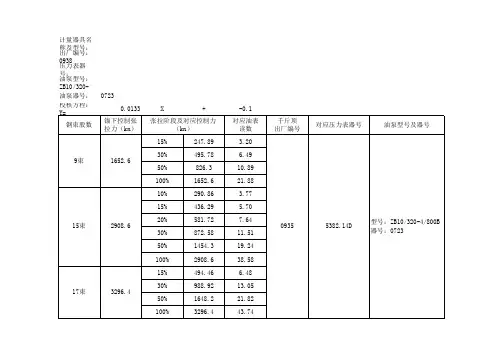
设计伸长量复核一、计算公式及参数：1、预应力平均张拉力计算公式及参数：式中：Pp—预应力筋平均张拉力（N）P—预应力筋张拉端的张拉力（N）X—从张拉端至计算截面的孔道长度（m）θ—从张拉端至计算截面的曲线孔道部分切线的夹角之和（rad）k—孔道每米局部偏差对摩檫的影响系数，取0.002μ—预应力筋与孔道壁的摩檫系数，取0.142、预应力筋的理论伸长值计算公式及参数：式中：Pp—预应力筋平均张拉力（N）L—预应力筋的长度（mm）Ap—预应力筋的截面面积（mm2），取140 mm2Ep—预应力筋的弹性模量（N/ mm2），取1.95×105 N/ mm2二、伸长量计算：1、N1束一端的伸长量：单根钢绞线张拉的张拉力P=0.75×1860×140=195300NX=15.812/2=7.906mθ=11.4×π/180=0.19897radkx+μθ=0.002×7.906+0.14×0.19897=0.0436678Pp=195300×（1-e-0.0436678）/0.0436678=191097NΔL= PpL/（Ap Ep）=191097×7.906/（140×1.95×105）=55.3mm 与设计比较（55.3-57.1）/57.1=-3.15%2、N2束一端的伸长量：单根钢绞线张拉的张拉力P=0.75×1860×140=195300NX=15.821/2=7.9105mθ=12.8×π/180=0.2234radkx+μθ=0.002×7.9105+0.14×0.2234=0.047097Pp=195300×（1-e-0.047097）/0.047097=190772NΔL= PpL/（Ap Ep）=190772×7.9105/（140×1.95×105）=55.27mm 与设计比较（55.27-57.1）/57.1=-3.2%张拉时理论伸长量计算一、计算参数：1、K—孔道每米局部偏差对摩檫的影响系数：取0.0022、μ—预应力筋与孔道壁的摩檫系数：取0.143、Ap—预应力筋的实测截面面积：140 mm24、Ep—预应力筋实测弹性模量：2.02×105 N/ mm25、锚下控制应力：σk=0.75Ryb=0.75×1860=1395 N/ mm26、锚圈口摩阻损失：3.3%σk7、单根钢绞线张拉端的张拉控制力：P=103.3%×σkAp=201745N8、千斤顶计算长度：56cm9、工作锚长度：7cm10、限位板计算长度：2.5cm11、工具锚计算长度：不计二、张拉时理论伸长量计算：1、N1束一端的伸长量：X=15.812/2=7.906mL=7.906+（0.56+0.07+0.025）=8.561mθ=11.4×π/180=0.19897radkx+μθ=0.002×7.906+0.14×0.19897=0.0436678Pp=201745×（1-e-0.0436678）/0.0436678=197404NΔL= PpL/（Ap Ep）=197404×8.561/（140×2.02×105）=59.8mm 2、N2束一端的伸长量：X=15.821/2=7.9105mL=7.9105+（0.56+0.07+0.025）=8.566mθ=12.8×π/180=0.2234radkx+μθ=0.002×7.9105+0.14×0.2234=0.047097Pp=201745（1-e-0.047097）/0.047097=197068NΔL= PpL/（Ap Ep）=197068×8.566/（140×2.02×105）=59.7mm 第三章千斤顶张拉力与对应油表读数计算一、钢绞线的张拉控制应力：12根钢绞线束：σcon=103.3σk=103.3%×2343=2420.32KN二、1523号千斤顶张拉、0050号油表时：千斤顶回归方程：P=-0.35+0.01035F式中：P——油压表读数（MPa）F——千斤顶拉力（KN）(1)、10%σcon=242.032 KN时：P=-0.35+0.01035F=-0.35+0.01035×242.032=2.16MPa(2)、40%σcon=968.13KN时：P=-0.35+0.01035F=-0.35+0.01035×968.13=9.67 MPa(3)、70%σcon=1694.22KN时：P=-0.35+0.01035F=-0.35+0.01035×1694.22=17.19 MPa(4)、100%σcon=2420.32KN时：P=-0.35+0.01035F=-0.35+0.01035×2420.32=24.7 MPa三、1524号千斤顶张拉、0054号油表时：千斤顶回归方程：P=0.21+0.01022F：式中：P——油压表读数（MPa）F——千斤顶拉力（KN）(1)、10%σcon=242.032KN时：P=0.21+0.01022F=0.21+0.01022×242.032=2.68 MPa(2)、40%σcon=968.13KN时：P=0.21+0.01022F=0.21+0.01022×968.13=10.10 MPa (3)、70%σcon=1694.22KN时：P=0.21+0.01022F=0.21+0.01022×1694.22=17.52 MPa (4)、100%σcon=2420.32KN时：P=0.21+0.01022F=0.21+0.01022×2420.32=24.95 MPa 四、1525号千斤顶张拉、0077号油表时：千斤顶回归方程：P=-0.47+0.01024F：式中：P——油压表读数（MPa）F——千斤顶拉力（KN）(1)、10%σcon=242.032KN时：P=-0.47+0.01024F=-0.47+0.01024×242.032=2.0 MPa (2)、40%σcon=968.13KN时P=-0.47+0.01024F=-0.47+0.01024×968.13=9.44 MPa (3)、70%σcon=1694.22KN时：P=-0.47+0.01024F=-0.47+0.01024×1694.22=16.88 MPa (4)、100%σcon=2420.32KN时：P=-0.47+0.01024F=-0.47+0.01024×2420.32=24.31 MPa 五、1526号千斤顶张拉、0064号油表时：千斤顶回归方程：P=-0.05+0.01021F：式中：P——油压表读数（MPa）F——千斤顶拉力（KN）(1)、10%σcon=242.032KN时：P=-0.05+0.01021F=-0.05+0.01021×242.032=2.42 MPa (2)、40%σcon=968.13KN时P=-0.05+0.01021F=-0.05+0.01021×968.13=9.83 MPa (3)、70%σcon=1694.22KN时：P=-0.05+0.01021F=-0.05+0.01021×1694.22=17.24 MPa (4)、100%σcon=2420.32KN时：P=-0.05+0.01021F=-0.05+0.01021×2420.32=24.66 MPa。

关于检校张拉千斤顶的回归方程式关于检校张拉千斤顶的回归方程式阐明由（一）式至（二）式的转换过程以及a 与b 的出处（一） Y = a + b X （试验室公式，旨在求得a 、b 。

） 试验室数据（“顶压机”法）油缸面积571.48cm 2=57148mm 20.4（1.0）级压力表读数MPa(Y) 千斤顶压 力值(KN) （理论计算）压力机读数KN(X)校正系数实测值理论值=K1.00≤K ≤1.051 2 3 均值 A B C D E F G i1 5 285.7 272.1 1.05 i2 10 571.5 544.3 1.05 i3 15 857.2 816.4 1.05 i4 20 1143.0 1088.6 1.05 i5 25 1428.7 1360.7 1.05 i6 30 1714.4 1632.8 1.05 i7 35 2000.2 1905.0 1.05 i8 40 2285.9 2177.0 1.05 i9 45 2571.7 2449.2 1.05 in …首先计算相关系数])([])([2222Y Y n X X n YX XY n ∑-∑*∑-∑∑*∑-∑=γ ≥0.9999计算公式：截距 222)(X n X X Y X XY a ∑-∑∑*∑-∑*∑=斜率 22)(Xn X XYn Y X b ∑-∑∑-∑*∑= 说明：①“Σ”读“西格玛”是“∑=ni 11”的简化。

表示与a 、b 相关的数据（即“回归因素”）Y 或X 由 i 1=5MPa(或272.1KN)……至i 9=45MPa(或2449.2KN)……i n =……之总和。

② n 表示数据量即因数发生的次数，此处n=9。

例如：22229124515105+++=∑= i y 。

()22914515105+++=⎪⎭⎫⎝⎛∑= i y 。

()2.2449454.816153.544101.2725991⨯+⨯+⨯+⨯=∑= i YX n 。

后张法钢绞线理论伸长值计算公式说明及计算示例后张法预应力钢绞线在张拉过程中，主要受到以下两方面的因素影响：一是管道弯曲影响引起的摩擦力，二是管道偏差影响引起的摩擦力，导致钢绞线张拉时，锚下控制应力沿着管壁向梁跨中逐渐减小，因而每一段的钢绞线的伸长值也是不相同的。

《公路桥梁施工技术规范》(JTJ 041-2000)中关于预应筋伸长值的计算按照以下公式：ΔL=（1）Pp=（2）式中：ΔL—各分段预应力筋的理论伸长值（mm）；Pp—各分段预应力筋的平均张拉力，注意不等于各分段的起点力与终点力的平均值（N）；L—预应力筋的分段长度（mm）；Ap—预应力筋的截面面积（mm2）；Ep—预应力筋的弹性模量（Mpa）；P—预应力筋张拉端的张拉力，将钢绞线分段计算后，为每分段的起点张拉力，即为前段的终点张拉力（N）；θ—从张拉端至计算截面曲线孔道部分切线的夹角之和，分段后为每分段中各曲线段的切线夹角和（rad）；x—从张拉端至计算截面的孔道长度，整个分段计算时x等于L（m）；k—孔道每束局部偏差对摩擦的影响系数（1/m），管道弯曲及直线部分全长均应考虑该影响；μ—预应力筋与孔道壁之间的磨擦系数，只在管道弯曲部分考虑该系数的影响。

从公式（1）可以看出，钢绞线的弹性模量Ep是决定计算值的重要因素，它的取值是否正确，对计算预应力筋伸长值的影响较大。

Ep的理论值为Ep=（1.9~1.95）×105Mpa，而将钢绞线进行检测试验，弹性模量则常出现Ep’=（1.96~2.04）×105Mpa的结果，这是由于实际的钢绞线的直径都偏粗，而进行试验时并未用真实的钢绞线面积进行计算，采用的是偏小的理论值代入公式进行计算，根据公式Ep=可知，若Ap 偏小，则得到了偏大的Ep ’值，虽然Ep ’并非真实值，但将其与钢绞线理论面积相乘所计算出的ΔL 却是符合实际的，所以要按实测值Ep ’进行计算。

公式（2）中的k 和μ是后张法钢绞线伸长量计算中的两个重要的参数，这两个值的的大小取决于多方面的因素：管道的成型方式、力筋的类型、表面特征是光滑的还是有波纹的、表面是否有锈斑，波纹管的布设是否正确，偏差大小，弯道位置及角度等等，各个因素在施工中的变动很大，还有很多是不可能预先确定的，因此，摩擦系数的大小很大程度上取决于施工的精确程度。

千斤顶回归方程公式计算油表读数嘿，朋友们！今天咱们来唠唠千斤顶回归方程算油表读数这神奇的事儿。

你看啊，就好像厨师要根据菜谱精准下料一样，咱们得用这个方程来准确读出油表数。

回归方程嘛，就像是一把神秘的钥匙，能打开油表读数这个小秘密的大门。

一般来说，这个方程可能是类似y = ax + b这样简单又神奇的式子（这里只是简单举例哈）。

想象一下，这个x就像是一个调皮的小精灵，它代表着某个影响油表读数的因素，可能是千斤顶的压力值之类的。

而a呢，就像是这个小精灵的魔法棒的放大倍数，要是a很大，那就像小精灵施展了超强魔法，对y的影响可不得了。

b呢，就像是这个魔法世界里的一个基础常数，不管怎么变，它就在那儿，像个固执的小老头。

那怎么根据这个方程算油表读数呢？假如说我们知道了x的值，就像抓住了小精灵。

那计算y（也就是油表读数）就像是让小精灵按照a的魔法棒规则，再加上那个固执小老头b的影响，然后得出结果。

比如说，x是5，a是2，b是3，那y就等于2×5 + 3 = 13，就好像是13这个数字从方程这个魔法阵里蹦了出来。

这油表读数啊，就像一个捉摸不定的小怪兽。

有时候，它可能因为一些小误差，就像小怪兽打了个喷嚏，让我们得到的数值有点偏差。

这时候，回归方程就像一个驯兽师，通过不断调整a和b这些参数，把小怪兽重新拉回到正确的轨道上。

再比如说，这个回归方程就像是一个超级精确的导航仪，而油表读数是我们要到达的目的地。

如果方程里的系数出了问题，就像导航仪指错了路，那我们可就找不到正确的油表读数这个目的地啦。

有时候，我感觉这个计算过程就像一场有趣的猜数字游戏。

我们通过回归方程这个线索，在一堆可能的油表读数中找到那个正确的答案。

方程中的每个参数都是这个游戏的小提示，我们要像聪明的侦探一样，根据这些提示破解油表读数的密码。

而且啊，这个油表读数和回归方程的关系就像一对小冤家。

如果我们没有好好对待方程，读数就会跟我们闹别扭，给我们一个错误的结果。

千斤顶张拉力与对应油表读数计算一、锚下控制应力：σK=0.75fpa=1395Mpa二、预应力筋的截面面积Ap=140mm2三、单根钢绞线张拉的张拉力F=σk*Ap=1395Mpa*140mm2=195300N四、25m箱梁钢绞线的张拉控制力：3根钢绞线束：F1=3*σK*AP=3*195.3KN=585.9KN4根钢绞线束：F2=4*σK*AP=4*195.3KN=781.2KN5根钢绞线束：F3=5*σK*AP=5*195.3KN=976.5KN五、1#千斤顶张拉、9953号油表时：千斤顶回归方程：P=0.0478F(KN)+0.66式中：P——油压表读数（Mpa）F——千斤顶拉力（KN）油压表读数计算如下六、1#千斤顶张拉、5247号油表时：千斤顶回归方程：P=0.0484F(KN)-0.25式中：P——油压表读数（Mpa）F——千斤顶拉力（KN）油压表读数计算如下七、2#千斤顶张拉、7297号油表时：千斤顶回归方程：P=0.0482F(KN)+0.22式中：P——油压表读数（Mpa）F——千斤顶拉力（KN）油压表读数计算如下八、2#千斤顶张拉、7424号油表时：千斤顶回归方程：P=0.0502F(KN)+0.21式中：P——油压表读数（Mpa）F——千斤顶拉力（KN）油压表读数计算如下伸长量验算一、锚下控制应力：σK=0.75fpa=1395Mpa二、预应力筋的截面面积Ap=140mm2三、单根钢绞线张拉的张拉力P=σk*Ap=1395Mpa*140mm2=195300N四、预应力平均张拉力计算公式及参数：Pp=P*（1-e-（kx+μθ）/（kx+μθ）式中：Pp——预应力筋的平均张拉力（N）P ——预应力筋张拉端的张拉力（N）X——从张拉端至计算截面的孔道长度（m）θ——从张拉端至计算截面的曲线孔道部分切线的夹角之和（rad）K——孔道每米局部偏差对摩擦的影响系数，取0.0015μ——预应力筋与孔道壁的摩擦系数，取0.25五、预应力筋的理论伸长量计算公式及参数：△L=Pp*L/Ap*Ep式中：Pp——预应力筋平均张拉力（N）L——预应力筋的长度（mm）Ap——预应力筋的截面面积（mm2），取140mm2Ep——预应力筋的弹性模量（N/mm2），取1.95×105Pa六、伸长量计算：（1）20m中跨一片预制箱梁1、N1束一端的伸长量：从张拉端开始分段计算至跨径中心线：X工作长=0.46m ；X斜直=6.384m；X曲=2.88m ;X直=0.437m；θ=5.5*π/180=0.09599rad伸长量计算如下：设计伸长量为139mm2、N2束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至跨径中心线：X工作长=0.46m；X斜直=4.923m；X曲=2.88m；X直=1.915m；θ=5.5*π/180=0.09599rad伸长量计算如下：设计伸长量为138mm3、N3束一端的伸长量：从张拉端开始分段计算至跨径中心线：X工作长=0.46m；X斜直=1.066m；X曲=0.733m；X直=7.783m；θ=1.4*π/180=0.024435rad伸长量计算如下：设计伸长量137mm（2）20m边跨一片预制箱梁1、N1束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至跨径中心线：X工作长=0.46m；X斜直=4.772m；X曲=2.88m；X直=2.097m；θ=5.5*π/180=0.09599rad伸长量计算如下：设计伸长量139mm2、N2束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至跨径中心线：X工作长=0.46m；X斜直=4.556m；X曲=3.49m；X直=4.267m;θ=5*π/180=0.0873rad伸长量计算如下：设计伸长量为173mm3、N3束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至跨径中心线：X工作长=0.46m；X斜直=2.961m；X曲=3.49m；X直=5.867mθ=5*π/180=0.0873rad伸长量计算如下：设计伸长量为173mm4、N4束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至跨径中心线：X工作长=0.46m；X斜直=1.017m；X曲=0.733m；X直=10.501mθ=1.4*π/180=0.0244rad伸长量计算如下：设计伸长量为173mm（3）25m箱梁顶板束钢绞线1、T1束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至桥墩中心线：X工作长=0.46m；X直=3.5m；伸长量△L工作长=P*L/（Ap*Ep）=195300*0.46/（140*1.95*105）=3.29mm 伸长量△L直=P*L/（Ap*Ep）=195300*3.5/（140*1.95*105）=25.03mm △L=（△L工作长+△L直）*2=（3.29+25.03）*2=56.64mm设计伸长量为50mm2、T2束一端的伸长量：单根钢绞线张拉的张拉力p=0.75×1860×140=195300N从张拉端开始分段计算至桥墩中心线：X工作长=0.46m ；X直=7m；伸长量△L工作长=P*L/（Ap*Ep）=195300*0.46/（140*1.95*105）=3.29mm 伸长量△L直=P*L/（Ap*Ep）=195300*7/（140*1.95*105）=50.07mm△L=（△L工作长+△L直）*2=（3.29+50.07）*2=106.72mm设计伸长量为106.72mm亲爱的各位老师，您们好！我叫xxx,我的毕业论文题目是《数字图书馆资源共享中云计算的现状、颈瓶与对策研究》。

千斤顶回归方程计算千斤顶是一种常见的力学装置，用于提升重物或增加力量。

它的原理是利用杠杆原理，通过加大力的面积，减小力的大小，实现力的放大。

在力学中，我们可以使用千斤顶回归方程，来计算千斤顶的力的放大率。

F1=F2×(A2/A1)其中，F1是千斤顶的输出力，F2是千斤顶的输入力，A1是千斤顶的输出面积，A2是千斤顶的输入面积。

1.千斤顶是一个理想的杠杆系统，没有摩擦和能量损失。

2.千斤顶是一个密封的容器，没有液体泄漏。

3.千斤顶的活塞（或活塞杆）是刚性的，没有形变。

4.应力分布是均匀的。

根据上述假设，我们可以得出以下结论：1.千斤顶的输出力与输入力成正比。

即输入力越大，输出力也越大。

2.千斤顶的输出力与输入面积成反比。

输入面积越大，输出力越小。

使用千斤顶回归方程可以有以下应用：1.工业应用：在工业领域中，千斤顶常被用于提升或移动重物。

通过计算千斤顶的力的放大率，可以确定所需的输入力，以实现所需的输出力。

2.汽车维修：千斤顶也被广泛用于汽车维修中。

通过计算千斤顶的力的放大率，可以确定所需的输入力，以提升汽车或更换轮胎等操作。

3.建筑领域：在建筑领域中，千斤顶也被用于提升和稳定建筑结构。

通过计算千斤顶的力的放大率，可以确定所需的输入力，以满足建筑结构的需求。

需要注意的是，在实际应用中，由于存在摩擦、能量损失和系统的复杂性等因素，千斤顶的输出力可能会有一定的损失。

因此，在使用千斤顶回归方程计算时，应考虑到这些因素，并进行相应的修正。

总结而言，千斤顶回归方程是一种用于计算千斤顶的力的放大率的工具。

它通过输入力和输出力以及输入面积和输出面积之间的关系，帮助我们确定所需的输入力，以实现所需的输出力。

这对于工业、汽车维修和建筑等领域来说，都有着重要的应用价值。