关于检校张拉千斤顶的回归方程式共4页

60吨千斤顶回归方程式
欧伯巴顶是一种常见的悬臂梁设备，它实施了很多重要的工程，这也是一种比
较常见的大型设备。

现在，我们研究的是60吨千斤顶的回归方程式，说明如何计
算其工作效率。

悬臂梁设备的工作原理是通过传动机构，使吊杆上的机头和下方支座间结构，
给吊杆及吊杆上装在钢绞线上的暂停发动机提供动力，利用钢绞线起升吊杆上的吊头。

清楚地知道60吨千斤顶的回归方程式，可以准确计算出其工作效率。

在数学上，60吨千斤顶的回归方程式可以用以下公式表示：M=q*h1*h2/h3，
其中M为吊头重量（60吨），q为起升的速度，h1、h2、h3分别为支座的高度和
绞线的高度。

可以看出，它的计算特别复杂，它是通过不同参数的加权相乘得出的，我们通过改变参数的值来调节工作效率。

此外，60吨千斤顶的回归方程式也允许我们改变设备的结构来实现其燃料消
耗的最小化，从而节约成本。

因此可以看出，60吨千斤顶的回归方程式不仅可以
用来计算其工作效率，还可以用来优化设备的结构，从根本上改善其工作性能。

使用60吨千斤顶的回归方程式可以准确地测试设备的性能，更重要的是，能
够最大程度地提高工作效率，使设备能够实现最低燃料消耗和最优工作绩效。

因此，60吨千斤顶的回归方程式的存在，对于悬臂梁设备的研究和开发，起着重要的作用。

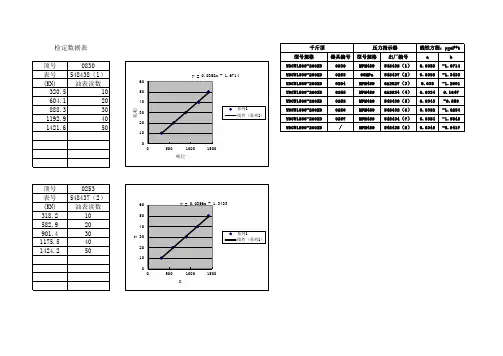
关于检校张拉千斤顶的回归方程式关于检校张拉千斤顶的回归方程式阐明由（一）式至（二）式的转换过程以及a 与b 的出处（一） Y = a + b X （试验室公式，旨在求得a 、b 。

） 试验室数据（“顶压机”法）油缸面积571.48cm 2=57148mm 20.4（1.0）级压力表读数MPa(Y) 千斤顶压 力值(KN) （理论计算）压力机读数KN(X)校正系数实测值理论值=K1.00≤K ≤1.051 2 3 均值 A B C D E F G i1 5 285.7 272.1 1.05 i2 10 571.5 544.3 1.05 i3 15 857.2 816.4 1.05 i4 20 1143.0 1088.6 1.05 i5 25 1428.7 1360.7 1.05 i6 30 1714.4 1632.8 1.05 i7 35 2000.2 1905.0 1.05 i8 40 2285.9 2177.0 1.05 i9 45 2571.7 2449.2 1.05 in …首先计算相关系数])([])([2222Y Y n X X n YX XY n ∑-∑*∑-∑∑*∑-∑=γ ≥0.9999计算公式：截距 222)(X n X X Y X XY a ∑-∑∑*∑-∑*∑=斜率 22)(Xn X XYn Y X b ∑-∑∑-∑*∑= 说明：①“Σ”读“西格玛”是“∑=ni 11”的简化。

表示与a 、b 相关的数据（即“回归因素”）Y 或X 由 i 1=5MPa(或272.1KN)……至i 9=45MPa(或2449.2KN)……i n =……之总和。

② n 表示数据量即因数发生的次数，此处n=9。

例如：22229124515105+++=∑= i y 。

()22914515105+++=⎪⎭⎫⎝⎛∑= i y 。

()2.2449454.816153.544101.2725991⨯+⨯+⨯+⨯=∑= i YX n 。

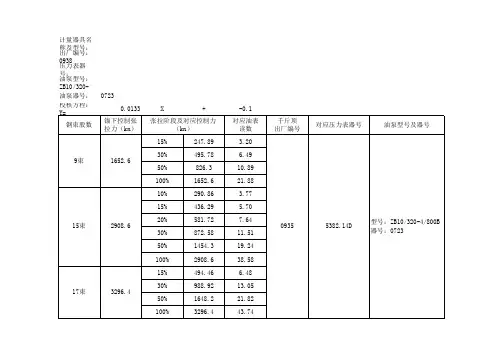
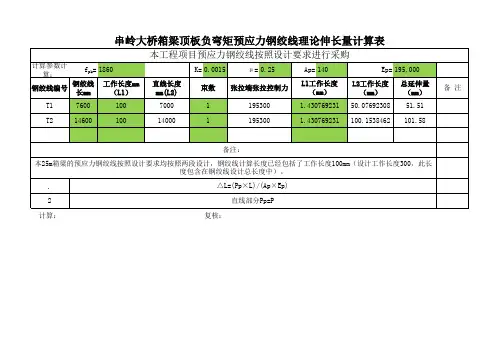
沈阜开发大道（丹霍公路十大线至新民外环段）改扩建工程第八合同段施工空心板张拉力、油表读数及伸长值大连四方公路工程有限公司沈阜开发大道改扩建工程第八合同段项目经理部2011年05月25日20米空心板张拉力、油表读数及伸长值计算说明书一、φs15.2钢铰线初始张拉力（20%）及油表读数计算1、初始张拉力（20%）的计算P（20%）=σS其中：σ—控制应力1395MPaS—钢筋有效面积140mm22、油表读数计算1#千斤顶y=0.2191x-1.4133（回归方程由检测报告提供）2#千斤顶y=0.2209x-0.7867（回归方程由检测报告提供）其中：y—指示器示值x—负荷二、φs15.24钢铰线控制张拉力（100%）及油表读数计算1、控制张拉力（100%）的计算P（20%）=σS×100%其中：σ—控制应力1395MPaS—为钢筋有效截面积140mm22、油表读数计算1#千斤顶y=0.2191x-1.41332#千斤顶y=0.2209x-0.7867其中：y—指示器示值x—负荷详细计算数值见下表20m空心板张拉力及油表读数3、理论伸长值的计算ΔL=P/E×L其中：ΔL—理论伸长值(mm)P—设计控制应力P=1395 MPaE—弹性模量E=1.95×105MPaL—张拉台座夹具至夹具距离L=66400mmΔL=1395/（1.95×105）×66400=475mm4、实测值为ΔL实=ΔL初+ΔL终其中：ΔL初为初张拉力（20%）对应的钢铰线伸长值，实际取理论计算值的20%，ΔL初=95mmΔL终相对于初张拉时的实际伸长值实测伸长值与理论伸长值的差值按照桥梁施工技术规范要求应控制在±6% 以内，否则应暂停张拉，待查明原因并采取措施予以调整后，方可继续张拉。

13米空心板张拉力、油表读数及伸长值计算说明书一、φs12.7钢铰线初始张拉力（20%）及油表读数计算1、初始张拉力（20%）的计算P（20%）=σS其中：σ—控制应力1395MPaS—钢筋有效面积98.7mm22、油表读数计算1#千斤顶y=0.2191x-1.4133（回归方程由检测报告提供）2#千斤顶y=0.2209x-0.7867（回归方程由检测报告提供）其中：y—指示器示值x—负荷二、φs12.7钢铰线控制张拉力（100%）及油表读数计算1、控制张拉力（100%）的计算P（20%）=σS×100%其中：σ—控制应力1395MPaS—为钢筋有效截面积98.7mm22、油表读数计算1#千斤顶y=0.2191x-1.41332#千斤顶y=0.2209x-0.7867其中：y—指示器示值x—负荷详细计算数值见下表13m空心板张拉力及油表读数3、理论伸长值的计算ΔL=P/E×L其中：ΔL—理论伸长值(mm)P—设计控制应力P=1395 MPaE—弹性模量E=1.95×105MPaL—张拉台座夹具至夹具距离L=56700mmΔL=1395/（1.95×105）×56700=406mm4、实测值为ΔL实=ΔL初+ΔL终其中：ΔL初为初张拉力（20%）对应的钢铰线伸长值，实际取理论计算值的20%，ΔL初=81mmΔL终相对于初张拉时的实际伸长值实测伸长值与理论伸长值的差值按照桥梁施工技术规范要求应控制在±6% 以内，否则应暂停张拉，待查明原因并采取措施予以调整后，方可继续张拉。

第五章千斤顶校验规程第一节基本原理千斤顶，特别是大吨位千斤顶，常用于预应力砼施工中预应力钢绞线等的张拉。

由于千斤顶对外显示不是活塞上的力值而是液压油的压力值，这样在张拉钢绞线张拉时不方便。

钢绞线的张拉是以力为控制参数的，故校验的第一个任务就是建立千斤顶液压油压力值同千斤顶向外提供的力值之间的关系；一般地，这种关系是线性关系。

另外，由于千斤顶活塞与活塞环之间存在摩擦阻力，单纯以液压油压力来计算千斤顶提供的力值是不恰当的，同时，若活塞与活塞环之间的摩擦阻力过大，也不能保证千斤顶的正确计量，这也是在千斤顶的校验要处理的问题，也就是要限制千斤顶的摩阻系数不大于．．．．。

．．．．．．．．．．．．．1.05一般地，校验千斤顶前，应先校准油压表；只有经校准的油压表才能用在千斤顶上。

在千斤顶上的油压表一般是1.5级精度，这样，在最不利的情况下，互换油压表后的误差也不会超过3.0%，这种精度是能满足施工要求的。

故在理论上用于千斤顶上的油压表可以互换使用，前提条件是油压表必须校准合格。

第二节校验荷载级数确定千斤顶在使用时，往往达不到其最大的吨位，因此在校验时，也不一定要校验到最大吨位。

因此校验荷载级数可这样确定：根据使用要求，确定本次校验的最大压力Pa，则级间压力差为Pa/10，同时，再向最大压力之外加上两荷载级，即两个Pa/10，这样校验荷载级数共有12级。

第三节校验过程1、千斤顶的准备在校验之前，应让千斤顶的活塞自由往复运动数次，一是查看千斤顶是否完好，二是确定千斤顶活塞与活塞环之间是否有异物，造成摩擦阻力过大。

如有故障，应先排除故障。

然后要查找千斤顶的铭牌或档案，查出它的公称活塞面积备用。

2、校验时，将千斤顶置于反力架上，测力计或传感器器置于千斤上方（可选用三等精度的测力计或传感器），用垫块适当地垫高千斤顶或测力计，使用千斤顶活塞能顶上反力架，如图1所示。

启动千斤顶油压泵，使压力表清零。

若是小吨位、小行程的千斤顶，可以用试验室的压力机或万能材料试验机做反力架。