现代控制理论-第7章
- 格式:doc
- 大小:834.00 KB
- 文档页数:49



现代控制理论智慧树知到课后章节答案2023年下长安大学长安大学绪论单元测试1.下列语句中,不正确的是()。
A:现代控制理论是建立在状态空间法基础上的一种控制理论,是自动控制理论的一个主要组成部分,可以解决经典控制理论不能解决的所有控制难题。
B:现代控制理论比经典控制理论所能处理的控制问题要广泛得多,包括线性系统和非线性系统,定常系统和时变系统,单变量系统和多变量系统;C:20世纪50年代中期,空间技术的迅速发展迫切要求建立新的控制原理,以解决诸如把宇宙火箭和人造卫星用最少燃料或最短时间准确地发射到预定轨道一类的控制问题;D:在现代控制理论中,对控制系统的分析和设计主要是通过对系统的状态变量的描述来进行的,基本的方法是时间域方法;答案:现代控制理论是建立在状态空间法基础上的一种控制理论,是自动控制理论的一个主要组成部分,可以解决经典控制理论不能解决的所有控制难题。
2.通过测量输出量,产生一个与输出信号存在函数关系的信号的元件称为()。
A:给定元件B:放大元件C:反馈元件D:比较元件答案:比较元件3.闭环控制系统的控制方式为()。
A:按扰动信号控制B:按输入信号控制C:按偏差信号控制D:按反馈信号控制答案:按偏差信号控制4.经典控制理论描述系统的数学模型是由高阶线性常微分方程演变来的传递函数,适合分析和设计下列哪种系统()A:非线性系统B:单输入单输出系统C:线性定常系统D:多输入多输出系统答案:单输入单输出系统;线性定常系统5.现代控制理论是建立在状态空间法基础上的一种控制理论,是自动控制理论的一个主要组成部分,比经典控制理论所能处理的控制问题要广泛得多,适合分析和设计下列哪种系统()A:非线性系统B:线性时变系统C:多输入多输出系统D:线性定常系统答案:非线性系统;线性时变系统;多输入多输出系统;线性定常系统第一章测试1.系统状态空间实现中选取状态变量不是唯一的,其状态变量的个数是唯一的()A:对 B:错答案:对2.多输入-多输出系统的U-Y 间的传递函数为()A:错 B:对答案:对3.由一个状态空间模型可以确定多个传递函数。

第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
1图P2.2解 这是一个物理系统,采用机理分析法求状态空间表达式会更为方便。
令()f t 为输入量,即u f =,1M ,2M 的位移量1y ,2y 为输出量, 选择状态变量1x =1y ,2x = 2y ,3x =1dy dt,24dyx dt =。

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解:()()22232321s s s s s s s++ =++ ? ?D S N S ; ()3r 2,1,2E -:223381s s s s s s ??++ ?-- ? ???;()3r 2,3,3E :223051s s s s s ??++ ?- ? ???;()3r 1,3,2E s --:01051s s ?? ?- ? ;()3r 2,1,5E s -:01001s ?? ?;()3r 3,1,1E -:01000s ?? ? ? ???;()1r 2,3E :01000s ?? ? ? ???;()1r 1,2E :00100s ?? ?;所以⼀个gcrd 为001s ??;取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。
1.9 求转移矩阵t A e (1)已知1141??=A ,根据拉⽒反变换求解转移矩阵tA e 。
(2) 已知412102113-?? ?= ? ?-??A ,根据C-H 有限项展开法求解转移矩阵t A e 。
解:(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -,得1,233,1λλ== 对1,23λ=,可以计算1,2()2rank λ=A I -,所以该特征值的⼏何重数为1。

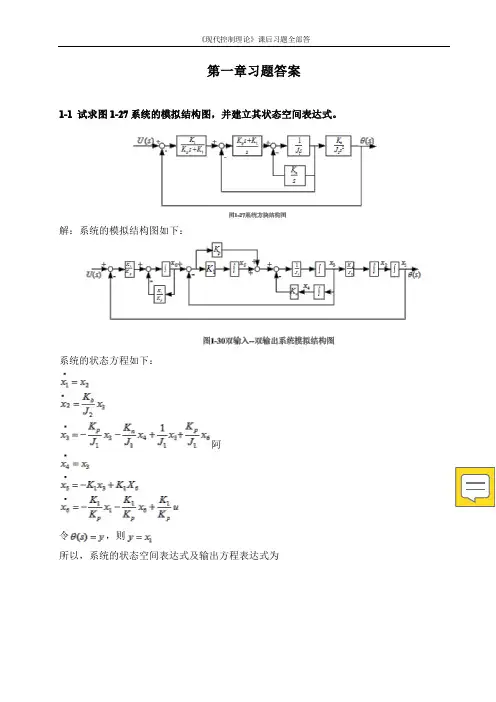
第一章习题答案1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:系统的状态方程如下:阿令,则所以,系统的状态空间表达式及输出方程表达式为状态变量的状态方程,和以电阻上的电压作为输出量的输出方程。
解:由图,令,输出量有电路原理可知:既得写成矢量矩阵形式为:1-4两输入,,两输出,的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令,则有相应的模拟结构图如下:1-6(2)已知系统传递函数,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:1-7给定下列状态空间表达式(1)画出其模拟结构图(2)求系统的传递函数解:(2)1-8求下列矩阵的特征矢量(3)解:A的特征方程解之得:当时,解得:令得(或令,得)当时,解得:令得(或令,得)当时,解得:令得1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)解:A的特征方程当时,解之得令得当时,解之得令得当时,解之得令得约旦标准型1-10已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果解:(1)串联联结(2)并联联结1-11(第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-12已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u的系数b(即控制列阵)为(1)解法1:解法2:求T,使得得所以所以,状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数。
(2)A=解:第一种方法:令则,即。
求解得到,当时,特征矢量由,得即,可令当时,特征矢量由,得即,可令则,第二种方法,即拉氏反变换法:第三种方法,即凯莱—哈密顿定理由第一种方法可知,2-5下列矩阵是否满足状态转移矩阵的条件,如果满足,试求与之对应的A阵。




现代控制理论智慧树知到课后章节答案2023年下哈尔滨工程大学哈尔滨工程大学绪论单元测试1.经典控制理论以单变量线性定常系统作为主要的研究对象,以时域法作为研究控制系统动态特性的主要方法。
A:对 B:错答案:错2.1892年俄国数学家李亚普诺夫发表了论文《运动稳定性的一般问题》,用严格的数学分析方法全面地论述了稳定性问题。
A:对 B:错答案:对3.现代控制理论以多变量线性系统和非线性系统作为研究对象,以时域法,特别是状态空间方法作为主要的研究方法。
A:对 B:错答案:对4.研究系统控制的一个首要前提是建立系统的数学模型,线性系统的数学模型主要有两种形式,即时间域模型和频率域模型。
A:对 B:错答案:对5.下述描述中哪些作为现代控制理论形成的标志()。
A:用于系统的整个描述、分析和设计过程的状态空间方法 B:随机系统理论中的Kalman滤波技术 C:最优控制中的Pontriagin极大值原理和Bellman动态规划 D:最优控制理论的产生答案:用于系统的整个描述、分析和设计过程的状态空间方法;随机系统理论中的Kalman滤波技术;最优控制中的Pontriagin极大值原理和Bellman动态规划第一章测试1.输入输出描述是描述系统输入变量和输出变量关系的模型。
A:对 B:错答案:对2.状态空间描述能完全表征系统的一切动力学特征。
A:对 B:错答案:对3.系统的状态是指能够完全表征系统时间域行为的一个最小内部变量组。
A:对 B:错答案:对4.系统的状态空间描述是唯一的。
A:错 B:对答案:错5.坐标变换是指将系统在状态空间的一个基底上的表征,化为另一个基底上的表征。
A:错 B:对答案:对6.当状态空间描述中的A矩阵有相同的特征值时,一定不能将其化成对角规范形。
A:错 B:对答案:错7.并联组合系统的传递函数矩阵为各并联子系统的传递函数矩阵之和。
A:对 B:错答案:对8.若两个子系统输出向量的维数相同,则可实现反馈连接。
《现代控制理论》习题第一章 控制系统的状态空间模型1.1 考虑以下系统的传递函数:656)()(2+++=s s s s U s Y试求该系统状态空间表达式的能控标准形和可观测标准形。
1.2 考虑下列单输入单输出系统:u y y yy 66116=+++试求该系统状态空间表达式的对角线标准形。
1.3 考虑由下式定义的系统:Cxy Bu Ax x=+=式中]11[,213421=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=C B A ,--试将该系统的状态空间表达式变换为能控标准形。
1.4 考虑由下式定义的系统:Cxy Bu Ax x=+=式中]011[,10030021101=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C B A ,--试求其传递函数Y(s)/U(s)。
1.5 考虑下列矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001100001000010A试求矩阵A 的特征值λ1,λ2,λ3 和λ4。
再求变换矩阵P ,使得),,,(diag 43211λλλλ=-AP P第二章 状态方程的解2.1 用三种方法计算下列矩阵A 的矩阵指数函数At e 。
1) ⎥⎦⎤⎢⎣⎡--=5160A; 2) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6116100010A2.2 计算下列矩阵的矩阵指数函数At e 。
1) ⎥⎦⎤⎢⎣⎡=0010A ; 2) ⎥⎦⎤⎢⎣⎡=1002--A ; 3) ⎥⎦⎤⎢⎣⎡-=0110A ; 4) ⎥⎦⎤⎢⎣⎡=1021A5) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=200010011A ; 6) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=210010001A ; 7) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000100010A2.2 给定线性定常系统Ax x=式中⎥⎦⎤⎢⎣⎡--=2310A且初始条件为⎥⎦⎤⎢⎣⎡-=11)0(x试求该齐次状态方程的解x (t )。
2.4 已知系统方程如下[]xy u x x 11015610-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=求输入和初值为以下值时的状态响应和输出响应。
《现代控制理论参考答案》第三版第一章答案1-1 试求图 1-27 系统的模拟结构图,并建立其状态空间表达式。
U (s) +K1+Kps K1+1K b(s)-K p s K1s-J1s J2s2-K ns图1-27系统方块结构图解:系统的模拟结构图如下:K p+K1+x x++1x K b x xU(s)K p-K1+-J1J2(s) --K1x4K nK p图1-30双输入--双输出系统模拟结构图系统的状态方程如下:x1x2x 2K b x3J 2x3K p K nx41K p x3J1x5x6 J1J1J1x4x3x5K 1 x3K1X6x6K1 x1K1 x6K1 u K p K p K p令(s)y ,则y x1所以,系统的状态空间表达式及输出方程表达式为0 1 0 0 0 0x 1K b 00 x 1 0x 2J 2 0x 2K p K n 1 K p 0 x 3 0x 3J 1 J 1 J J 1 0 ux 4 x 40 1 0 0 0 00 K 1 0 0 K 1 x 5x 5K 1x 6x 6K 1 0K 1 K pK pK px 1x 2 y1 0 0 00 0x 3 x 4 x 5x 61-2 有电路如图 1-28 所示。
以电压 u(t ) 为输入量, 求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻 R 2上的电压作为输出量的输出方程。
R1 L1 L2i1i2C--------- UUc R2---------图1-28 电路图解:由图,令 i 1 x 1 , i 2x 2 , u cx 3 ,输出量 y R 2 x 2x 1R 1 x 11x 3 1 uR 1 x 1 L 1 x 1 x 3uL 1 L 1L 1R 21x 3L 2 xR 2 x 2 x 3x 2x 2有电路原理可知:2既得L 2L 2x 1x 2 C x 3x 31x 11x 2CCy R 2 x 2写成矢量矩阵形式为:。
第六次课小结一、 Lyapunov 意义下的稳定性问题基本概念● 平衡状态的概念● Lyapunov 意义下的稳定性定义(稳定,一致稳定,渐进稳定,一致渐进稳定,大范围渐进稳定等)● 纯量函数的正定性,负定性,正半定性,负半定性,不定性 ● 二次型,复二次型(Hermite 型)二、 Lyapunov 稳定性理论● 第一方法 ● 第二方法三、 线性定常系统的Lyapunov 稳定性分析● 应用Lyapunov 方程Q PA P AH-=+来进行判别稳定性四、 线性定常系统的稳定自由运动的衰减率性能估计● 衰减系数,一旦定出min η,则可定出)(x V 随时间t 衰减上界。
● 计算min η的关系式五、 离散时间系统的状态运动稳定性及其判据● 离散系统的大范围淅近稳定判据,Lyapunov 稳定判据在离散系统中的应用六、 线性多变量系统的综合与设计的基本问题●问题的提法●性能指标的类型●研究的主要内容七、极点配置问题●问题的提出●可配置条件●极点配置算法5.2.5 爱克曼公式(Ackermann ’s Formula) 考虑由式(5.1)给出的系统,重写为Bu Ax x +=假设该被控系统是状态完全能控的,又设期望闭环极点为n s s s μμμ===,,,21 。
利用线性状态反馈控制律Kx u -=将系统状态方程改写为x BK A x )(-=(5.14)定义BK A A -=~则所期望的特征方程为)())((~11121=++++=---=-=+-**--*n n n nn a s a sa s s s s A sI BK A sI μμμ由于凯莱-哈密尔顿定理指出A ~应满足其自身的特征方程,所以0~~~)~(**11*1*=++++=--I a A a A a A A n n n n φ (5.15)我们用式(5.15)来推导爱克曼公式。
为简化推导,考虑n = 3的情况。
需要指出的是,对任意正整数,下面的推导可方便地加以推广。
考虑下列恒等式22333222~~)(~~)(~~ABK A ABK BK A A BK A A A BK ABK A BK A A BKA A I I ---=-=--=-=-== 将上述方程分别乘以)1(,,,*0*0*1*2*3=a a a a a ,并相加,则可得32*1*2*3~~~AA a A a I a +++-+--+-+=32*1*2*3)~()(A A BK ABK A a BK A a I a22~~ABK A ABK BK A --------+++=BK A A BK a ABK a BK a A A a A a I a 2*1*1*232*1*2*3~2~~A BK A ABK -- (5.16)参照式(5.15)可得0)~(~~~*32*1*2*3==+++A A A a A a I a φ也可得到0)(*32*1*2*3≠=+++A A A a A a I a φ将上述两式代入式(5.16),可得BKA A ABK ABK a A BK A BK a BK a A A 2*12*1*2**~~~)()~(------=φφ由于0)~(*=A φ,故BKA A K K a AB A K A K a K a B A 2*12*1*2*)~()~~()(+++++=φ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=K A K K a A K A K a K a B A AB B ~~~][*12*1*22 (5.17)由于系统是状态完全能控的,所以能控性矩阵][2B A AB B Q =的逆存在。
在式(5.17)的两端均左乘能控性矩阵Q 的逆,可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=-K A K K a A K A K a K a A B A AB B ~~~)(][*12*1*2*12φ上式两端左乘[0 0 1],可得KK A K K a A K A K a K a A B A AB B =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=-~~~]100[)(]][100[*12*1*2*12φ重写为)(][]100[*12A B A AB B K φ-=从而给出了所需的状态反馈增益矩阵K 。
对任一正整数n ,有)(]][1000[*11A B AAB B K n φ--= (5.18)式(5.18)称为用于确定状态反馈增益矩阵K 的爱克曼方程。
------------------------------------------------- [例5.1] 考虑如下线性定常系统Bu Ax x +=式中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,651100010B A利用状态反馈控制Kx u -=,希望该系统的闭环极点为s = -2±j 4和s = -10。
试确定状态反馈增益矩阵K 。
首先需检验该系统的能控性矩阵。
由于能控性矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==316161010][2B A AB B Q所以得出det Q = -1,因此,rank Q = 3。
因而该系统是状态完全能控的,可任意配置极点。
下面,我们来求解这个问题,并用本章介绍的3种方法中的每一种求解。
方法1:第一种方法是利用式(5.13)。
该系统的特征方程为:156651101||3221323=+++=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=-a s a s a s s s s s s sA sI因此1,5,6321===a a a期望的特征方程为2006014)10)(42)(42(*3*22*1323=+++=+++=+++-+a s a s a s s s s s j s j s因此200,60,14*3*2*1===a a a参照式(5.13),可得]855199[]6145601200[=---= K方法2:设期望的状态反馈增益矩阵为][321k k k K =并使||BK A sI +-和期望的特征多项式相等,可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+-651100010000000||s s s BK A sI 321[100k k k ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+ 20060141)5()6(65110012312233321+++=++++++=++++--=s s s k s k s k s k s k k ss因此2001,605,146123=+=+=+k k k从中可得8,55,199321===k k k或]855199[=K方法3:第三种方法是利用爱克曼公式。
参见式(5.18),可得)(]][100[*12A B A AB B K φ-=由于I A A A A 2006014)(23*+++=φ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=11743771598855199100010001200651100010606511000101465110001023且⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=316161010][2B A AB B可得]855199[11743771598855199001016165]100[117437715988551993161610100]100[1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-K显然,这3种方法所得到的反馈增益矩阵K 是相同的。
使用状态反馈方法,正如所期望的那样,可将闭环极点配置在s = -2±j 4和s = -10处。
------------------------------------------------------------------------------应当注意,如果系统的阶次n 等于或大于4,则推荐使用方法1和3,因为所有的矩阵计算都可由计算机实现。
如果使用方法2,由于计算机不能处理含有未知参数n k k k ,,,21 的特征方程,因此必须进行手工计算。
5.2.6 注释对于一个给定的系统,矩阵K 不是唯一的,而是依赖于选择期望闭环极点的位置(这决定了响应速度与阻尼),这一点很重要。
注意,所期望的闭环极点或所期望状态方程的选择是在误差向量的快速性和干扰、测量噪声的灵敏性之间的一种折衷。
也就是说,如果加快误差响应速度,则干扰和测量噪声的影响通常也随之增大。
如果系统是2阶的,那么系统的动态特性(响应特性)正好与系统期望的闭环极点和零点的位置联系起来。
对于更高阶的系统,期望的闭环极点位置不能和系统的动态特性(响应特性)联系起来。
因此,在决定给定系统的状态反馈增益矩阵K 时,最好通过计算机仿真来检验系统在几种不同矩阵(基于几种不同的期望特征方程)下的响应特性,并且选出使系统总体性能最好的矩阵K 。
5.3 利用MATLAB 求解极点配置问题用MATLAB 易于求解极点配置问题。
现在我们来求解在例5.1中讨论的同样问题。
系统方程为Bu Ax x +=式中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100651100010B A , 采用状态反馈控制Kx u -=,希望系统的闭环极点为s =μi(i=1,2,3),其中10,42,42321-=--=+-=μμμj j现求所需的状态反馈增益矩阵K 。
如果在设计状态反馈控制矩阵K 时采用变换矩阵P ,则必须求特征方程|s I-A |=0的系数1a 、2a 、和3a 。
这可通过给计算机输入语句P = poly(A )来实现。
在计算机屏幕上将显示如下一组系数:则)4(3),3(2),2(1321P a a P a a P a a ======。
为了得到变换矩阵P ,首先将矩阵Q 和W 输入计算机,其中][2B A AB B Q =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=001011112a a a W 然后可以很容易地采用MATLAB 完成Q 和W 相乘。
其次,再求期望的特征方程。
可定义矩阵J ,使得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1000042004200000321j j J μμμ从而可利用如下poly(J )命令来完成,即因此,有)4(3),3(2),2(1*3*2*1Q aa a Q aa a Q aa a ======即对于*i a ,可采用aai 。
故状态反馈增益矩阵K 可由下式确定:1112233][-***---=P a a a a a a K或aaaaaaaaa=--K-3[P(inv())3*2]211采用变换矩阵P求解该例题的MATLAB程序如MATLAB Program 5.1所示。
Q=[B A*B A^2*B];%*****Check the rank of matrix Q*****rank(Q)ans=3%*****Since the rank of Q is 3, arbitrary pole placement is% possible *****%*****Obtain the coefficients of the characteristic polynomial%|sI-A|. This can be done by entering statement poly(A)*****JA=poly(A)JA=1.0000 6.0000 5.0000 1.0000a1=JA(2);a2=JA(3);a3=JA(4);%*****Define matrices W and P as follows*****W=[a2 a1 1;a1 1 0;1 0 0];P=Q*W;%*****Obtain the desired chracteristic polynomial by defining%the following matrix J and entering statement poly(J)*****J=[-2+j*4 0 0;0 -2-j*4 0;0 0 -10];JJ=poly(J)JJ=1 14 60 200aa1=JJ(2);aa2=JJ(3);aa3=JJ(4);%*****State feedback gain matrix K can be given by *****K=[aa3-a3 aa2-a2 aa1-a1]*(inv(P))K=199 55 8%*****Hence, k1,k2,and k3 are given by *****k1=K(1),k2=K(2),k3=K(3)如果采用爱克曼公式来确定状态反馈增益矩阵K ,必须首先计算矩阵特征方程φ(A )。