机械振动4两自由度系统的动力学方程1-2全解

两个自由度系统的振动理论曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、两个自由度系统的自由振动2、两个自由度系统的受迫振动1、两个自由度系统的自由振动（1）模型的简化同一物体的振动可以简化为不同的振动模型。

C研究上下平移振动研究前后颠簸振动两个自由度系统的自由振动模型112122222122()00mxk k x k x m x k x k x ++-=üý-+=þ&&&&2212121m k d m k c m k k b ==+=，，令方程变为：11221200xbx cx x dx dx +-=-+=&&&&，根据微分方程理论，可设上列方程组的解为：)sin()sin(21q w q w +=+=t B x t A x ，其中：A 、B 是振幅；ω为角频率，θ是初始相位角。

将上式代入微分方程组，得到：)sin()sin()sin(0)sin()sin()sin(22=+++++-=+-+++-q w q w q w w q w q w q w w t dB t dA t B t cB t bA t A 整理后得到：0)(0)(22=++-=--B d dA cB A b w w ，系统振动时，方程组具有非零解, 则方程组的系数行列式必须等于零，即：22=----ww d dc b —频率行列式①固有频率1、两个自由度系统的自由振动)()(24=-++-c b d d b w w 行列式展开后得到：—系统的本征方程，又称为频率方程21,22b d w +=m 2b d +=m i ω2的两个根都是实数，而且都是正数。

ii ω2的第一个根较小，称为第一固有频率。

iii ω2的第二个根较大，称为第二固有频率。

结论：两个自由度系统具有两个固有频率，这两个固有频率只与系统的质量和刚度等参数有关，而与振动的初始条件无关。

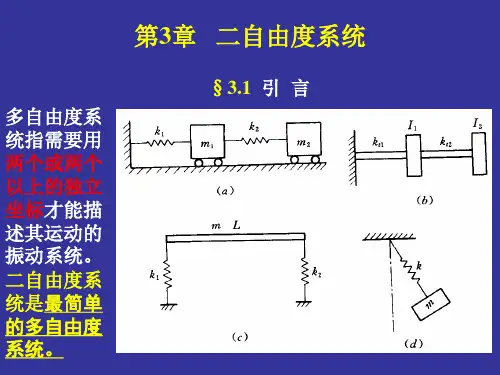
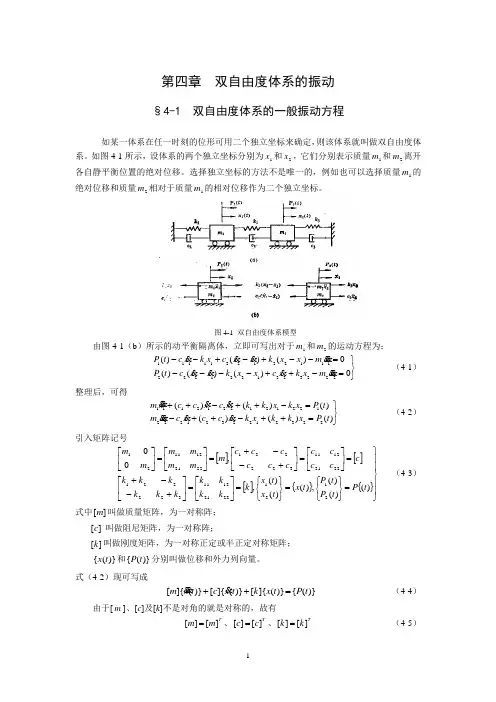
第四章 双自由度体系的振动§4-1 双自由度体系的一般振动方程如某一体系在任一时刻的位形可用二个独立坐标来确定，则该体系就叫做双自由度体系。

如图4-1所示，设体系的两个独立坐标分别为1x 和2x ，它们分别表示质量1m 和2m 离开各自静平衡位置的绝对位移。

选择独立坐标的方法不是唯一的，例如也可以选择质量1m 的绝对位移和质量2m 相对于质量1m 的相对位移作为二个独立坐标。

图4-1 双自由度体系模型由图4-1（b ）所示的动平衡隔离体，立即可写出对于1m 和2m 的运动方程为：⎭⎬⎫=-++----=--+-+--0)()()(0)()()(22232312212221112212211111xm x k x c x x k x x c t P x m x x k x x c x k x c t P （4-1）整理后，可得⎭⎬⎫=++-++-=-++-++)()()()()()(22321223212221221212212111t P x k k x k x c c x c xm t P x k x k k x c x c c x m （4-2）引入矩阵记号[][][]{}{}⎪⎪⎭⎪⎪⎬⎫=⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+--+=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+--+=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)()()(,)()()(,,00212122211211322221222112113222212221121121t P t P t P t x t x t x k k k k k k k k k k k c c c c c c c c c c c m m m m m m m （4-3）式中][m 叫做质量矩阵，为一对称阵；][c 叫做阻尼矩阵，为一对称阵；][k 叫做刚度矩阵，为一对称正定或半正定对称矩阵； )}({t x 和)}({t P 分别叫做位移和外力列向量。

1. 如右图系统受到力F 1(t)=0，F 2(t)=Fsin(wt)的 作用，试确定系统的稳态响应。

2. 图所示，弹簧质量系统在光滑水平面上自由振动。

试建立该振动系统的运动方程，求出系统固有频率和相应的主振型，并给出系统自由振动的通解。

3二自由度振动系统的运动方程为⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡--+⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡)()(1899182001212121t f t f x x xx 其中：t 以秒为单位；x 以米为单位。

已知系统的固有频率为ωn1,2=2.388,4.615 rad/s ，对应的振型矩阵为[]⎥⎦⎤⎢⎣⎡-=366.0366.111u 。

4 二自由度振动系统的运动方程为⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡--+⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡)()(1899182001212121t f t f x x x x其中：t 以秒为单位；x 以米为单位。

求系统的固有固有频率和振型向量m2m5． 写出系统的振动微分方程。

（当摆处于铅直位置时为静平衡位置，此时弹簧处于自然长度，系统作微幅振动）6. 图示为汽车的某理想化模型，车身简化作一刚性杆，质量为m ，质心在C 点，车身对质心的转动惯量为Jc 。

支撑系统简化为两个弹簧，弹簧常数分别为k 1k 和k 2。

假定汽车在纸面内运动，包括（1）车身的垂直运动x ；（2）车身绕其质心在纸面（纵向平面）内的旋转运动，即点头运动。

若k 1=k ，k 2=2k ；l 1=l 2=1,J 0=31ml 2。

请列出车身振动时的运动微分方程。

7．如图，已知m 2＝2×m 1=m ，k 3=2k 1=2k 2=2k ，x 10=1.2,x 20=10x＝20x ＝0，试求系统的固有频率，主振型以及相应。

8．已知:⎢⎣⎡=][m,激振力频率ω=3rad/s,9．一辆汽车重。

试确定10．一重块2W 自高h 处自由落下，然后与弹簧-质量系统112k gW k --一起作自由振动，如图3-8所示，试求其响应。